Способ угловой засечки кратко

Основы геодезии

О геодезии и разный полезный материал для геодезистов.

Прямая угловая засечка

Сначала рассмотрим так называемый общий случай прямой угловой засечки, когда углы β1 и β2 измеряются на двух пунктах с известными координатами, каждый от своего направления с известным дирекционным углом (рис.2.6).

Исходные данные: XA, YA, αAC,
XB, YB, αBD

Измеряемые элементы: β 1 , β2

Неизвестные элементы: X , Y

Если αAC и αBD не заданы явно, нужно решить обратную геодезическую задачу сначала между пунктами A и C и затем между пунктами B и D .

Графическое решение. От направления AC отложить с помощью транспортира угол β1 и провести прямую линию AP; от направления BD отложить угол β2 и провести прямую линию BP ; точка пересечения этих прямых является искомой точкой P.

Аналитическое решение. Приведем алгоритм варианта, соответствующий общему случаю засечки:

1. вычислить дирекционные углы линий AP и BP
(2.14) ,
(2.15)
2. написать два уравнения прямых линий

для линии AP Y – YA= tgα1 * ( X – XA ),

для линии BP Y – YB= tgα2 * ( X – XB ) (2.16)
3. решить систему двух уравнений и вычислить неизвестные координаты X и Y:
(2.17) ,
(2.18)

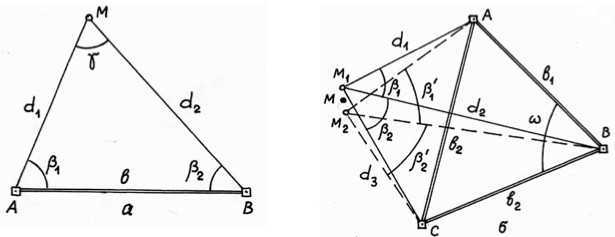
Частным случаем прямой угловой засечки считают тот случай, когда углы β1 и β2 измерены от направлений AB и BA, причем угол β1 – правый, а угол β2 – левый (в общем случае засечки оба угла – левые) – рис.2.7.

Решение прямой угловой засечки методом треугольника соответствует частному случаю засечки. Порядок решения при этом будет такой:

1. решить обратную задачу между пунктами A и B и получить дирекционный угол αAB и длину b линии AB,
2. вычислить угол γ при вершине P, называемый углом засечки,
(2.19)
3. используя теорему синусов для треугольника APB:
(2.20)

вычислить длины сторон AP (S1) и BP (S2) ,
4. вычислить дирекционные углы α1 и α2:
(2.21)
5. решить прямую задачу от пункта A к точке P и для контроля – от пункта B к точке P.

Для вычисления координат X и Y в частном случае прямой угловой засечки можно использовать формулы Юнга:
(2.22)

От общего случая прямой угловой засечки нетрудно перейти к частному случаю; для этого нужно сначала решить обратную геодезическую задачу между пунктами A и B и получить дирекционный угол αAB линии AB и затем вычислить углы в треугольнике APB при вершинах A и B

BAP = αAB – ( αAC + β1 ) и ABP = ( αBD + β2 ) – αBA .

Для машинного счета все рассмотренные способы решения прямой угловой засечки по разным причинам неудобны. Один из возможных алгоритмов решения общего случая засечки на ЭВМ предусматривает следующие действия:

1. вычисление дирекционных углов α1 и α2 ,
2. введение местной системы координат X’O’Y’ с началом в пункте A и с осью O’X’, направленной вдоль линии AP, и пересчет координат пунктов A и B и дирекционных углов α1 и α2 из системы XOY в систему X’O’Y’ (рис.2.8):

X’A = 0 , Y’A = 0 ,
(2.23) ,
(2.24) ,
3. запись уравнений линий AP и BP в системе X’O’Y’ :
(2.26)

и совместное решение этих уравнений:
(2.27)
4. перевод координат X’ и Y’ из системы X’O’Y’ в систему XOY:
(2.28)

Так как Ctgα2′ = – Ctgγ и угол засечки γ всегда больше 0, то решение (2.27) всегда существует.

Источник

Способы разбивочных работ

Способ прямой и обратной угловых засечек. Чаще всего эти способы применяют для выноса недоступных точек, а также точек, находящихся на значительных расстояниях от геодезической основы.

В способе прямой угловой засечки (см. рис. а) положение точки М определяют с исходных пунктов А и В геодезической основы построением в каждой из них горизонтальных углов β1 и β2, которые являются разбивочными элементами. Указанные углы строят на местности по правилам, изложенным в § 88. В данной схеме целесообразно использовать одновременно два теодолита. При этом положение проектной точки фиксируют по команде двух наблюдателей при положениях КЛ, а затем – при положениях КП. После фиксирования среднего положения точки М выполняют контрольное измерений углов β1 и β2.

Необходимо иметь в виду, что величина угла γ при точке М не должна быть малой и слишком большой. Оптимальным углом, при котором вынос точки может быть выполнен с меньшей погрешностью, является γ ≈109 0 − 110 0 при примерно равных расстояниях от исходных точек до точки М. То есть следует стремиться обеспечить симметричную схему построения точки М. Кроме того, для повышения точности построения проектной точки, а также для контроля её построения, вынос проектной точки на местность выполняют часто с двух базисов геодезической разбивочной основы.

Во многих случаях бывает сложно из одного приема вынести точку М с заданной точностью в её проектное положение. В таких случаях используют способ замкнутого треугольника. Вынос точки осуществляют последовательными приближениями. Для этого с максимально возможной точностью выполняют построение точки М, затем несколькими приёмами измеряют все углы треугольника, уравнивают углы и вычисляют координаты точки М из решения по формулам прямой угловой засечки. Полученные координаты сравнивают с проектными и при недопустимых отклонениях в их значениях определяют поправки (редукции) в положение точки М и смещают последнюю в проектное положение. Для контроля снова измеряют углы и выполняют аналогичные вычисления.

Вынос проектной точки способами прямой и обратной угловых засечек: а) способ прямой угловой засечки; б) способ обратной угловой засечки

Вынос на местность проектной точки способом полярных координат

Вынос на местность проектной точки способом проектного полигона

Метод последовательных приближений используют и в способе обратной угловой засечки (см. рис. б). Предварительно точку М выносят на местность и измеряют при ней углы β1 и β2. По формулам обратной угловой засечки определяют координаты точки М и сравнивают их с проектными. При необходимости положение точки М редуцируют на величины отклонений по координатам Х и Y, точку М фиксируют в положении М₂ и снова уже в новой точке измеряют горизонтальные углы β а затем вычисляют координаты новой точки М. Все указанные действия выполняют до тех пор, пока задача качественного построения проектной точки не будет решена.

Способ полярных координат используют в тех случаях, когда проектные точки находятся сравнительно недалеко от точек геодезической основы. При этом предпочтительно, чтобы расстояния до них не превышали длины мерного прибора (ленты или рулетки).

На местности от исходного направления АВ (см. рис.) строят проектный угол β и проектное расстояние d, которые в данном способе являются разбивочными элементами.

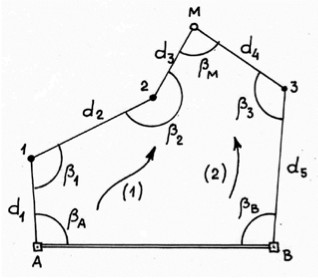
Проектная точка может находиться далеко от точек геодезической основы или не может быть вынесена по техническим условиям способами угловой засечки. В таких случаях к точке прокладывают полигонометрический ход (см. рис.), используя для этого последовательно расчётные проектные углы и проектные расстояния. Данный способ называют способом проектного полигона.

По двум ходам от базисной линии АВ геодезической основы получают два положения точки М из решения ходов (1) и (2). В качестве первого приближения вычисляют средние значения координат проектной точки. Затем в полученной точке М измеряют угол β_М и линии d₃ и d₄ и вычисляют координаты точки М в общей схеме замкнутого полигона. Если координаты точки М будут значительно отличаться от проектных, то определяют поправки (редукции) в положение точки М, точку смещают и снова измеряют угол β_М и линии d₃ и d₄. Из решения хода находят координаты точки М и сравнивают их с проектными. Такие действия выполняют до достижения необходимой точности построения проектной точки.

Вынос на местность проектной точки способом линейной засечки

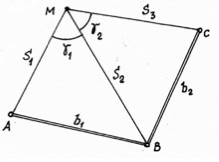
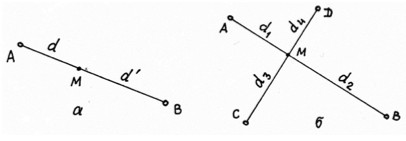
Способы створных засечек: а) способ створно-линейной засечки; б) способ створной засечки

При небольших расстояниях от проектной точки до точек геодезической основы удобно использовать способ линейной засечки, реализуемый с помощью двух или трёх рулеток (см. рис.). Разбивочными элементами в этом способе являются только расстояния S или горизонтальные проложения.

Для выноса осей сооружений удобно использовать способы створных засечек (см. рис.).

В схеме створно-линейной засечки (см. рис. а) положение точки М определяют на линии створа, образованного пунктами А и В геодезической основы. По линии створа проектным расстоянием d задают положение искомой точки М. При необходимости положение точки М может быть проконтролировано с другой точки створа. В точке А створа устанавливают теодолит, а в точке В – визирную цель (на штативе, с возможностью центрирования и горизонтирования).

В схеме створной засечки (см. рис. б) точку М задают на линии пересечения створов АВ и СD. Для повышения точности работу целесообразно выполнять одновременно двумя теодолитами и двумя визирными целями несколькими приёмами с перестановкой теодолитов и визирных целей. Для контроля измеряют расстояния от построенной точки до исходных пунктов геодезической основы.

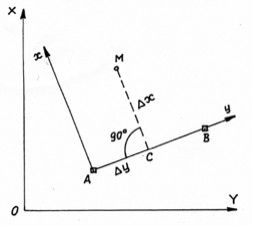
Обычно на строительной площадке имеется т.н. строительная сетка. В её системе координат задано положение всех осей (главных, основных и т.д.), а также всех главных (узловых) точек. В этом случае вынос проектных точек осуществляется в системе координат строительной сетки по приращениям координат Δx и Δy (см. рис.). В общегосударственной или местной системах координат ХОY используется система координат хАy строительной сетки c началом координат в точке А. Ось Аy задается исходным направлением на другую исходную точку (В) геодезической основы. Положение точки М определяется расстояниями Δx и Δy, т.е. приращениями координат в системе координат строительной сетки.

Разбивка точек сооружения от строительной сетки

Способ бокового нивелирования

Предварительно строят проектное расстояние Δy, устанавливают в полученной точке С теодолит, строят проектный угол β, равный 90 0 на точку М и в полученном направлении откладывают отрезок Δx. Для обеспечения более высокой точности построения точки меньшее из Δx и Δy следует строить в виде перпендикуляра, а большее – по створу исходной линии.

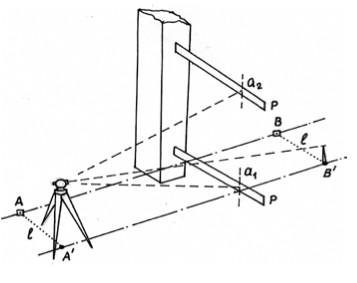
Вынос вертикальных осей конструкций выполняют способом бокового нивелирования (см. рис.). От оси АВ, на которой находится строительная конструкция, например, колонна, а небольшом расстоянии l строят линию А’В’, параллельную исходной линии АВ. В точке А’ устанавливают теодолит, который визируют на марку, находящуюся в точке В’. Перпендикулярно к оси колоны последовательно на её основание и верх устанавливают рейку Р (с уровнем, ориентированным осью по продольной оси рейки) и берут отсчёты а₁ и а₂ по вертикальной нити сетки зрительной трубы. Равенство указанных отсчётов определяет вертикальность оси колонны. Если расхождение между отсчётами недопустимо, то положение вертикальной оси колонны выправляют.

Оставьте свой отзыв, комментарий или задайте вопрос

Источник

Расчет разбивочных элементов в геодезии

Практически каждое строительство начинается с составления чертежа будущего объекта и проведения разбивочных работ, задачей которых является перенос на местность основных элементов проектной документации.

После установки местоположения точек, выставляются соответствующие метки, указывающие точное место возведения зданий и сооружений. Для обеспечения максимальной точности переноса точек, специалисты строят проектные углы и откладывают расстояния, переносят отметки и уклоны.

Способов проведения разбивочных работ есть немало, выбор зависит от условий местности, типа и габаритов конструкций, точности перенесения точек.

Способы разбивочных работ

Боковое нивелирование

Применяется для выноса осей в процессе проведения детальной разбивки и при установке конструкций в проектное положение.

Пересечение проектной точки К с конструкцией рассчитывается следующим образом. От точек А и В откладываются равные отрезки l для получения точек А’, В’ и линии А’В’. Над точкой А’ выставляется теодолит и наводится на точку В’. К горизонтальной конструкции прикладывается рейка и перемещается так, чтобы отсчет по ней был равен l. Пятка рейки даст положение точки К. Также определяется и положение точки К’.

Способ полярных координат

Используется при разбивке сооружений с пунктов теодолитных и полигонометрических ходов, если расстояние между исходными и выносимыми точками небольшое.

Положение точки К на местности определяется при откладывании от линии АВ угла β и вдоль линии АК горизонтали d. Угол β = бА — бAK, где бА, бАК являются дирекционными углами линий АВ и АК соответственно.

Горизонтальное положение d выясняется по формуле

Проконтролировать правильность положения точки К можно, отложив угол β’ от линии ВА и провести линию d’.

Прямая угловая засечка

Здесь положение К определяется при помощи отложения опорной линии АВ и углов β1 и β2, как на чертеже. Базой для b есть сторона разбивочной сетки либо его значение. Проектные углы β1 и β2 вычисляются путем определения разности дирекционных углов.

Способ линейной засечки

Задействуется для разбивки осей строительных конструкций. При помощи рулетки от точки А откладывается d1, от точки В – d2, место пересечения линий обозначается точкой К, которая и является проектной.

Метод пересечения створов

Используется для выноса в натуру труднодоступных точек проекта, если применение других технологий невозможно. На местности створы Т1Т’1 и Т2Т’2 задаются точками их пересечения с опорными сторонами. Местоположение точек Т1 и Т2 определяется горизонтальными продолжениями d1 и d2 от точки В вдоль опорных линий ВА и ВС, а точек Т’1 и Т’2 – от точки Е вдоль линий EF и ED.

Способ прямоугольных координат

Востребован в случае, если геодезическую основу представляет строительная сетка, вершины которой закреплены на местности. Для выноса проектной точки К по линии AD откладывается отрезок d1, равный УК — УА и по перпендикуляру к AD – отрезок d2, равный Хк — ХА. Для построения отрезков и d2 теодолит выставляется над точкой А, путем перекрещивания нитей зрительной трубы наводится на точку D и от точки А – в створе линии AD, откладывается горизонтальное продолжение d1 для получения точки Р. Далее теодолит устанавливается над точкой Р и откладывается прямой угол APР’. По направлению РР’ от точки Р откладывается горизонталь d2 с выставлением и закреплением точки К.

Разбивочные работы довольно сложные и заказывать их лучше у профессионалов.

Организация «ГеоКомпани» предлагает широкий спектр услуг по геологическим и геодезическим изысканиям. Работаем по Москве и Московской области. Работы выполняются на высоком уровне качества, в сжатые сроки и по выгодным ценам. Консультации предоставляются по телефону +7-495-777-65-35 или WhatsApp . .

Источник