Способ цифрового представления информации

Как представить информацию в цифровых устройствах?

Под информацией в широком смысле принято понимать различные сведения о событиях в общественной жизни, явлениях природы, о процессах в технических устройствах. Она содержатся в нашей речи, в текстах книг и газет, в показаниях измерительных приборов и отображает разнообразие, присущее объектам и явлениям реального мира. Информацию, воплощенную и зафиксированную а некоторой материальной форме, называют сообщением и передают с помощью сигналов. Природа большинства физических величин такова, что они могут принимать любые значения в каком-то диапазоне (температура, давление, скорость и т.д.). Сигнал, отображающий эту информацию и возникающий на выходе соответствующего датчика, на любом временном интервале может иметь бесконечное число значений. Так как в данном случае непрерывный сигнал изменяется аналогично исходной информации, его обычно называют аналоговым, а устройства, в которых действуют такие сигналы – аналоговыми. Существуют также дискретные сообщения, параметры которых содержат фиксированный набор отдельных значений. А так как этот набор конечен, то и объем информации в таких сообщениях конечен.

На практике непрерывные сообщения можно представлять в дискретной форме. Непрерывность сообщений по величине не может быть реализована в связи с погрешностью источников и приемников информации и наличием помех в канале передали информации. Поэтому к непрерывным сигналам, отображающим сообщения, можно применять квантование по уровню и по времени, При квантовании по уровню совокупность возможных значений напряжения или тока заменяют конечным набором дискретных значений из этого интервала. Квантование по времени предусматривает замену непрерывного сигнала последовательностью импульсов, следующих через определенные промежутки временя (рис. 1), называемых тактовыми. Если тактовые интервалы выбраны соответствующим образом, то потери информации не происходит. При одновременном введении квантования по времени и по уровню амплитуда каждой выборки будет принимать ближайшее разрешенное значение из выбранного конечного набора значений. Совокупность всех выборок образует дискретный или цифровой сигнал. Каждое значение дискретного сигнала можно представить числом. В цифровой технике такой процесс называется кодированием (дискретизацией), а совокупность полученных чисел—кодом сигнала.

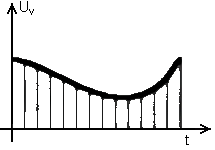
Рисунок 1

Вместо преобразования или передачи конкретных сигналов эти операции в устройствах цифровой техники могут быть выполнены над их кодами. При этом можно оперировать и аналоговыми сигналами, которые преобразуются в цифровые -с помощью АЦП.

Таким образом, дискретное сообщение состоит из набора чисел и символов (например, знаков «+» и «-»). Каждое число состоит из цифр. Способ записи чисел цифровыми знаками называется системой счисления. В цифровой технике используются так называемые позиционные системы счисления [20, 32]. Значение каждой входящей в число цифры зависит от ее положения в записи числа. Количество различных цифр, применяемых в позиционной системе, называют основанием системы. В зависимости от основания, позиционные системы счисления могут быть десятичными – с основанием 10, двоичными – с основанием 2 и др. Образовании чисел я любой системе счисления производят следующим образом: фиксируют позиции, называемые разрядами; каждому разряду присваивают свой вес h_i (где i номер разряда); h_i=p i (p – основание системы); в разрядах размещают цифры a_i Тогда любое число A может быть представлено в виде

Здесь n – число знаков до запятой; m – число знаков после запятой. Последовательность цифр.

можно рассматривать как код числа в заданной системе счисления.

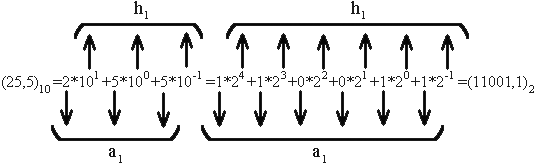
В цифровой технике наибольшее распространение получила двоичная сиcтема счисления, содержащая только цифры 0 и 1, п ее основанием служит число 2. Например, число 25,5 в десятичной и двоичной системах счисления может быть представлено в виде

Значительно реже используют восьмеричную и шестнадцатеричную системы. Их, в частности, применяют при составлении программ для более удобной. и короткой записи двоичных кодов команд, так как эти системы не требуют специальных операций для перевода в двоичную систему. Так, для перевода восьмеричного или шестнадцатеричного числа в двоичное каждую цифру переводимых чисел заменяют соответственно трех- и четырехразрядными двоичными числами. Например, восьмеричное число 726,4 в двоичной системе имеет. вид (726,4)₈== (111010110,1)₂. Для удобства изображения шестнадцатеричных цифр, больших 9, шесть старших цифр обычно изображают символами A, B, C, D, E, F.

В цифровых устройствах широко используют и так называемые двоично-десятичный код. В этом коде каждый разряд десятичного числа представляется в двоичном коде. В таблице 1 приведены коды чисел в различных системах счисления.

Код

Десятичный	Двоичный	Восьмеричный	Двоично-десятичный	Шестнадцатеричный
0	0	0	0	0
1	1	1	1	1
2	10	2	10	2
3	11	3	11	3
4	100	4	100	4
5	101	5	101	5
6	110	6	110	6
7	111	7	111	7
8	1000	10	1000	8
9	1001	11	1001	9
10	1010	12	0001 0000	A
11	1011	13	0001 0001	B
12	1100	14	0001 0010	C
13	1101	15	0001 0011	D
14	1110	16	0001 0100	E
15	1111	17	0001 0101	F
16	10000	20	0001 0110	10
17	10001	21	0001 0111	11
18	10010	22	0001 1000	12
19	10011	23	0001 1001	13
20	10100	24	0010 0000	14
21	10101	25	0010 0001	15
22	10110	26	0010 0010	16
23	10111	27	0010 0011	17
24	11000	30	0010 0100	18
25	11001	31	0010 0101	19
26	11010	32	0010 0110	1A
27	11011	33	0010 0111	1B
28	11100	34	0010 1000	1C
29	11101	35	0010 1001	1D
30	11110	36	0011 0000	1E
31	11111	37	0011 0001	1F
32	100000	40	0011 0010	20

Числа десятичной системы счисления нетрудно перевести в числа двоичной системы. При этом порядок перевода целых чисел отличается от перевода дробей. Чтобы перевести целое число Х с основанием 10 в систему с основанием 2, необходимо последовательно делить заданное число и получающиеся в процессе деления частные на 2 до тех, пор пока последнее частное не окажется меньше 2. Результат перевода записывается в виде последовательности цифр слева на право, начиная с последнего частного и кончая первым остатком (при этом число младшего разряда есть первый остаток). Все действия в процессе деления числа производят в десятичной системе счисления.

Источник

Способ цифрового представления информации

Электронные облака

Лекции

Рабочие материалы

Тесты по темам

Template tips

Задачи

Логика вычислительной техники и программирования

Лекция «Представление информации в компьютере. Структура внутренней памяти.»

Основные понятия: бит, байт, дискретность, отрицательные числа, дополнительный код, двоичные и шестнадцатеричные числа, целые и вещественные числа, мантисса, машинный порядок, нормализованное представление, машинное слово, адресуемость.

Биты и байты

Написание программ требует знаний организации всей системы компьютера. В основе компьютера лежат понятия бита и байта. Они являются тем средством, благодаря которым в компьютерной памяти представлены данные и команды.

Для выполнения программ компьютер временно записывает программу и данные в основную память. Компьютер имеет также ряд pегистров, которые он использует для временных вычислений.

Минимальной единицей информации в компьютере является бит.

Бит – ячейка памяти, хранящая один двоичный знак. Битовая структура памяти определяет первое свойство памяти – дискретность.

Бит может быть выключен, так что его значение есть нуль, или включен, тогда его значение равно единице. Единственный бит не может представить много информации в отличие от группы битов.

Байт — восемь расположенных подряд битов памяти.

Во внутренней памяти компьютера все байты пронумерованы. Нумерация начинается с нуля. Порядковый номер называется его адресом. В компьютере адреса обозначаются двоичным кодом. Используется также шестнадцатеричная форма обозначения адреса.

Двоичные числа

Так как компьютер может различить только нулевое и единичное состояние бита, то он работает системе исчисления с базой 2 или в двоичной системе. Фактически бит унаследовал свое название от английского «BInary digiT» (двоичная цифра).

Сочетанием двоичных цифр (битов) можно представить любое значение. Значение двоичного числа определяется относительной позицией каждого бита и наличием единичных битов. Ниже показано восьмибитовое число, содержащее все единичные биты:

Позиционные веса	128	64	32	16	8	4	2	1
Включенные биты	1	1	1	1	1	1	1	1

Двоичное число не ограничено только восемью битами. Если процессор использует 16-битовую архитектуру, он автоматически оперирует с 16-битовыми числами (2 в степени 16 минус 1 дает значение 65535), а для 32 бит — 4294967295 (2 в степени 32 минус 1) и так далее.

Двоичное сложение

Микрокомпьютер выполняет арифметические действия только в двоичном формате.

0 + 0 = 0
1 + 0 = 1
1 + 1 = 10
1 + 1 + 1 = 11

Обратите внимание на перенос единичного бита в последних двух операциях. Теперь, давайте сложим 01000001 и 00101010.(число 65 и число 42):

Двоичные	Десятичные
01000001	65
00101010	42
01101011	107

Проверьте, что двоичная сумма 01101011 действительно равна 107. Рассмотрим другой пример:

Двоичные	Десятичные
00111100	60
00110101	53
01110001	113

Представление целых чисел

Множество целых чисел, представимых в памяти ЭВМ, ограничено. Диапазон значений зависит от размера ячеек памяти, используемых для их хранения. В k-разрядной ячейке может храниться 2 k различных значений целых чисел.

Чтобы получить внутреннее представление целого положительного числа N, хранящегося в k-разрядном машинном слове, необходимо:

1) перевести число N в двоичную систему счисления;
2) полученный результат дополнить слева незначащими нулями до k разрядов

Отрицательные числа

Для записи внутреннего представления целого отрицательного числа (-N) необходимо:

1) получить внутреннее представление положительного числа N;
2) получить обратный код этого числа заменой 0 на 1 и 1на 0;
3) к полученному числу прибавить 1.

Данная форма представления целого отрицательного числа называется дополнительным кодом. Использование дополнительного кода позволяет заменить операцию вычитания на операцию сложения уменьшаемого числа с дополнительным кодом вычитаемого.

Двоичные разряды в ячейке памяти нумеруются от 0 до k справа налево. Старший, k-й разряд во внутреннем представлении любого положительного числа равен нулю, отрицательного числа – единице. Поэтому этот разряд называется знаковым разрядом.

Для представления отрицательного двоичного числа необходимо инвертировать все биты и прибавить 1. Рассмотрим пример:

Число 65	01000001
Инверсия	10111110
Плюс 1	10111111 (равно -65)

Сумма +65 и -65 должна составить ноль:

01000001	(+65)
10111111	(-65)
(1)00000000	0

Все восемь бит имеют нулевое значение. Перенос единичного бита влево потерян. Однако, если был перенос в знаковый разряд и из разрядной сетки, то результат является корректным.

Двоичное вычитание выполняется просто: инвертируется знак вычитаемого и складываются два числа. Вычтем, например, 42 из 65. Двоичное представление для 42 есть 00101010, и его двоичное дополнение: — 11010110:

65	01000001
+(-42)	11010110
23	(i)00010111

Результат 23 является корректным. В рассмотренном примере произошел перенос в знаковый разряд и из разрядной сетки.

Если справедливость двоичного дополнения не сразу понятна, рассмотрим следующие задачи: Какое значение необходимо прибавить к двоичному числу 00000001, чтобы получить число 00000000? В терминах десятичного исчисления ответом будет -1. Для двоичного рассмотрим 11111111:

00000001
11111111
Результат	(1)00000000

Игнорируя перенос (1), можно видеть, что двоичное число 11111111 эквивалентно десятичному -1 и соответственно:

0	00000000
-(+1)	-00000001
-1	11111111

Можно видеть также, каким образом двоичными числами представлены уменьшающиеся числа:

+3	00000011
+2	00000010
+1	00000001
0	00000000
-1	11111111
-2	11111110
-3	11111101

Фактически нулевые биты в отрицательном двоичном числе определяют его величину: рассмотрите позиционные значения нулевых битов как если это были единичные биты, сложите эти значения и прибавьте единицу.

Шестнадцатеричное представление

Представим, что необходимо просмотреть содержимое некоторых байт в памяти. Требуется определить содержимое четырех последовательных байт (двух слов), которые имеют двоичные значения. Так как четыре байта включают в себя 32 бита, то специалисты разработали «стенографический» метод представления двоичных данных. По этому методу каждый байт делится пополам и каждые полбайта выражаются соответствующим значением. рассмотрим следующие четыре байта:

Двоичное	0101	1001	001	0101	1011	1001	110	1110
Десятичное	5	9	3	5	11	9	12	14

Так как здесь для некоторых чисел требуется две цифры, расширим систему счисления так, чтобы 10=A, 11=B, 12=C, 13=D, 14=E, 15=F. Таким образом, получим более сокращенную форму, которая представляет содержимое вышеуказанных байт:

59

35

B9

CE

Такая система счисления включает «цифры» от 0 до F, и так как таких цифр 16, она называется шестнадцатеричным представлением.

Шестнадцатеричный формат нашел большое применение в языке ассемблера.

Если немного поработать с шестнадцатеричным форматом, то можно быстро привыкнуть к нему.

Следует помнить, что после шестнадцатеричного числа F следует шестнадцатеричное 10, что равно десятичному числу 16.

Заметьте также, что шестнадцатеричное 20 эквивалентно десятичному 32, шест. 100 -десятичному 256.

Машинное слово

Вся информация (данные) представлена в виде двоичных кодов. Для удобства работы введены следующие термины, обозначающие совокупности двоичных разрядов (см. табл.). Эти термины обычно используются в качестве единиц измерения объемов информации, хранимой или обрабатываемой в компьютере.

Источник