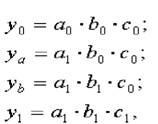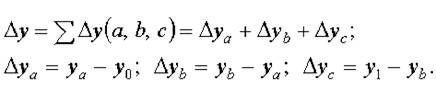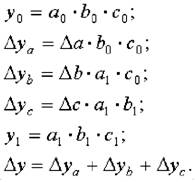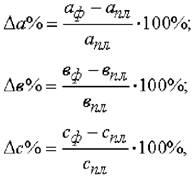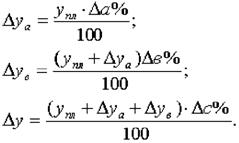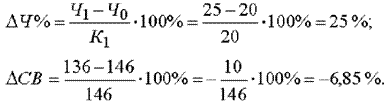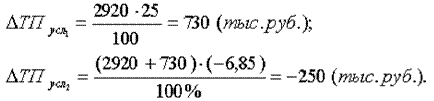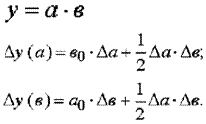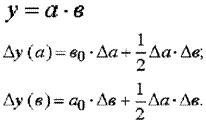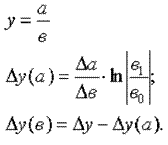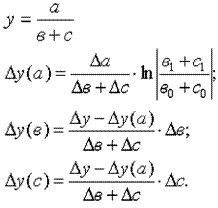Способ цепных подстановок суть

Метод цепных подстановок

Способ цепных подстановок может быть использован во всех типах детерминированных факторных моделей (аддитивные, мультипликативные, кратные, комбинированные) для расчёта величины влияния фактора на результат.

Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью рассчитывают ряд условных величин, которые учитывают изменение одного, двух и т.д. факторов, допуская, что остальные факторы не меняются. Сравнение величины результата до и после изменения уровня того или иного фактора позволяют элиминироваться от влияний всех факторов, кроме одного.

Алгоритм метода цепных подстановок для многофакторной мультипликативной модели

1. Рассчитываем плановый показатель: Y0 = a0 * b0 * с0* d0;

2. Далее рассчитывается система условных показателей:
Y_усл.1 = a1 * b0 * с0* d0;
Y_усл.2 = a1 * b1 * с0* d0;
Y_усл.3 = a1 * b1 * с1* d0;

3. Рассчитываем фактический показатель: Y1 = a1 * b1 * с1* d1;

4. Путем последовательного вычитания полученных показателей находим изменение результативного показателя за счет факторов:
ΔYа = Y_усл.1 – Y0;
ΔYb = Y_усл.2 – Y_усл.1;
ΔYс = Y_усл.3 – Y_усл.2;
ΔYd = Y1– Y_усл.3;
5. Рассчитываем общее отклонение фактического показателя от планового, которое равно сумме факторных отклонений:
ΔY = Y1 — Y0 = ΔYа + ΔYb + ΔYс + ΔYd

Рекомендации при использовании этого метода:
А) в первую очередь учитываются изменения количественных показателей, затем качественные;
Б) сначала учитываются факторы первого уровня подчинения, затем второго и т.д.

Пример . Исходные данные для расчета влияния факторов базисные: (y0 = 1,58; a0 = 12940; b0 = 8210 ) и фактические: (y1 = 1,53; a1 = 13950; b1 = 9124; ). Рассчитайте влияние на отклонение результативного показателя (y) каждого из определяющих его факторов (a, b).

Источник

Цепные подстановки в экономическом анализе

Вы будете перенаправлены на Автор24

Сущность метода цепных подстановок

Метод цепных подстановок, используемый в экономическом анализе, дает возможность измерить степень воздействия отдельных факторов на конечный результат их взаимодействия. Цепная подстановка представляет собой обобщающий (целевой) показатель, позволяющий определить отклонение фактических показателей от нормативного показателя (планового).

Метод расчета по цепным подстановкам является важным элементом методики экономического анализа, заключающийся в последовательной замене плановых величин одного из алгебраического слагаемого (сомножителя) фактической его величиной с сохранением в неизменном состоянии остальных показателей.

Метод цепных подстановок чаще всего используют при вычислении воздействия отдельных факторов на соответствующие совокупные показатели.

Этот метод экономического анализа используется в тех случаях, когда необходимо определить зависимость между изучаемыми явлениями, имеющую строго функциональный характер. Данная зависимость представляет собой прямую или обратно пропорциональную зависимость. В таком случае анализируемый совокупный показатель в качестве функции нескольких переменных изображается в форме алгебраической суммы, произведения или отношения (деление) одних показателей к другим.

Степень влияния соответствующего показателя можно выявить последовательным вычитанием, когда из второго расчета вычитают первый, из третьего вычитают второй и т.д. Первый расчет содержит все плановые величины, а последний фактические величины.

Отсюда выведено правило, которое заключается в том, что количество расчетов на единицу больше, чем количество показателей в расчетной формуле.

В процессе определения взаимодействия двух факторов (показателей) производят три расчета; трех факторов — делают четыре расчета; четырех факторов — осуществляют пять расчетов.

Готовые работы на аналогичную тему

Так как первый расчет состоит только из плановых величин, его результаты берут в готовом виде из планов предприятия (организации, объединений). Результат последнего расчета со всеми фактическими показателями берут из квартального или годового отчета. По этой причине на практике количество расчетов оказывается не на единицу больше, а на единицу меньше, то есть осуществляют только промежуточный расчет.

Алгоритм метода

Алгоритм метода цепных подстановок демонстрируется примером вычисления влияния изменения величины частных показателей на величину показателя, который представлен в виде следующей рассчитываемой формулы:

Данная формула представляет собой мультипликативную модель.

В этом расчете показатели с нулем соответствуют базисному периоду, поскольку он является индексом базисного показателя. Единица соответствует отчётному периоду и является индексом показателя отчётного периода.

При этом базисное значение $F$ равняется следующему равенству:

$F_0 = a_0 • b_0 • c_0$

Фактическое значение будет выглядеть следующим образом:

$F_1 = a_1 • b_1 • c_1$

При этом общее отклонение фактического показателя от базисного показателя выражается специальной формулой.

Очевидно, что данное равенство равняется сумме отклонений, которые получены под воздействием изменения частных показателей.

Изменения частных показателей можно вычислить посредством последовательных подстановок в формулу вычисления показателя $F$ по фактическим значениям параметров $a, b, c$ (вместо базисных показателей).

Проверить расчеты можно, сопоставив баланса отклонений, при этом общее отклонение фактических показателей от базисных должно приравниваться к сумме отклонений под воздействием изменения частных показателей.

Источник

Метод цепных подстановок в экономическом анализе — формулы и примеры расчетов

Метод цепных подстановок в экономическом анализе занимает ключевое место. Простые аналитические расчеты выявляют абсолютное или относительное (процентное) изменение важных показателей.

Но этого недостаточно: необходимо выяснить, как тот или иной фактор влияет на них. Для этих целей служит данный метод, который относится к детерминированным – определяющим вклад частей в целое.

Хотя сейчас существует возможность рассчитывать вклад факторов онлайн, но знание этого процесса помогает лучше уяснить его суть.

Общая характеристика метода

На изменение любого показателя действие оказывают чаще всего не один, а несколько причин или факторов.

Например, рост цен может происходить за счет:

снижения физического объема товара (в результате неурожая, разгула стихии, недостатка материалов для производства);

значительного роста спроса на продукцию;

увеличения себестоимости (вследствие увеличения стоимости сырья, трудозатрат).

Если найти разность между индексами цен за два года – 2019 и 2018, то будет известно, как повлияли все указанные выше факторы на инфляцию в текущем году.

При помощи факторного анализа с использованием способа цепных подстановок рассчитывается воздействие каждой причины. Станет известно, какое влияние она оказала на итог: увеличила или сократила его.

Эти знания помогут целенаправленно изменять тот фактор, который негативно подействовал на результат. Для решения экономических задач данная оценка очень важна.

Формула метода цепных подстановок

Расчет проводится по системе специальных формул, которые взаимосвязаны друг с другом. Они предусматривают постепенную замену множителей в формуле:

либо плановых на фактические;

либо базисных (за прошлый или иной другой базисный год) на отчетные (отчетный год).

Первый случай – итоговый показатель П находится произведением составляющих А, В, С, n:

Для трех множителей решение имеет вид, представленный в таблице.

Для плановых и фактических значений

Для базисных и отчетных

П(условие 1) = Афакт*Вплан*Сплан

П(условие 2) = Афакт*Вфакт*Сплан

П(условие 1) = Аотчет*Вбазис*Сбазис

П(условие 2) = Аотчет*Вотчет*Сбазис

Для базисных и отчетных значений, если базис – 2018 г., отчет – 2019 г.

П(условие 1) = А2019*В2018*С2018

П(условие 2) = А2019*В2019*С2018

Условный показатель – это когда его плановое значение заменяется на фактическое (или базисное – на отчетное): условие 1 – заменен первый множитель, условие 2 – второй, и так далее.

Базисный год – более ранний (например, 2018), отчетный – поздний (2019).

Далее рассчитывается, на сколько изменился показатель из-за изменения факторов А, В, С:

ΔП(А) = П(условие 1) – Пплан.

ΔП(В) = П(условие 2) – П(условие 1).

ΔП(С) = Пфакт – П(условие 2).

Если взяты значения базиса и отчетного периода, то:

ΔП(А) = П(условие 1) – Пбазис;

ΔП(В) = П(условие 2) – П(условие 1);

ΔП(С) = Потчет – П(условие 2).

В отличие от метода абсолютных разниц, здесь не надо считать отклонения сразу.

Второй случай – показатель П находится отношением двух элементов (П=А/В), то есть модель кратная.

Алгоритм решения, используемый при этом, показан в таблице:

Плановые (пл) и фактические (ф) значения

Базисные (б) и отчетные (о) значения

Расчет факторного влияния:

ΔП(А) = П(усл. 1) – Ппл;

ΔП(В) = Пф – П(усл. 1).

Третий случай – это смешанные виды моделей:

П = А*(В – С) и П = А/(В – С).

Решение идет аналогично: последовательно А, В и С заменяются на фактическое (или отчетное), после чего определяется их влияние, как показано для первых двух случаев.

Для балансовых соотношений практически не используется.

Пример решения задачи методом цепных подстановок

Задача 1

ООО «Экватор» в 2017 году продало 120 станков стоимостью 300 тыс. руб. каждый; в 2018 году – 119 станков по цене 330 тыс. руб. За счет каких факторов произошел рост выручки, а за счет каких – сокращение?

Сравниваются базисный период – за 2017 г. и отчетный – за 2018 г.

В(2017) = 120*300 = 36000 тыс. руб. – это значение выручки за базисный 2017 г.

В(условие 1) = 119*300 = 35700 тыс. руб. – это условная выручка, когда изменили только количество проданных станков – 119 вместо 120.

В(2018) = 119*330 = 39270 тыс. руб. – это выручка за отчетный 2018 год.

ΔВ(кол-во станков) = 35700 – 36000 = -300 тыс. руб. – за счет сокращения числа проданных станков выручка снизилась на 300 тыс. руб.

ΔВ(цена) = 39270 – 35700 = 3570 тыс. руб. – за счет того, что продажная цена поднялась, выручка увеличилась на 3570 тыс. руб.

ΔВ = 39270 – 36000 = 3270 тыс. руб.

ООО «Экватор» может увеличить выручку, если увеличит число проданных станков. Для этого надо выходить на новые рынки, привлекать новых покупателей.

Источник

Сущность метода цепных подстановок в экономическом анализе

Применяется для определения влияния отдельных факторов на результативный показатель. Может применяться тогда, когда зависимость между изучаемыми явлениями имеет строго функциональный характер – прямая или обратно пропорциональная зависимость. В этих случаях результативный показатель представляют как функцию нескольких переменных. Функцию можно представить в виде алгебраической суммы, произведения, частного.

Метод состоит в последовательной замене плановой величины факториального показателя фактической его величиной, все остальные показатели остаются неизменными, т.е. каждая подстановка связана с отдельным расчетом.

Степень влияния того или иного показателя определяется последующим вычитанием: из второго расчета вычитается первый, из третьего – второй, из четвертого – третий и так далее. В 1- ом расчете все величины плановые – базисные, а в последнем – все величины фактические. Число расчетов в этом методе на единицу больше, чем число факториальных показателей.

Общую схему метода можно представить следующим образом:

ΔТ= ΔТа+ ΔТв+ ΔТс+ ΔТd

При использовании метода очень важно обеспечит строгую последовательность подстановки, т.к. ее произвольное изменение может привести к неправильным выводам. В практике анализа в первую очередь выявляется влияние количественных, а затем качественных показателей. Если требуется определить степень влияния численности работников и производительности труда на размер выпуска продукции, то сначала устанавливается влияние количественного показателя (численность), а затем качественного (производительность). Если требуется определить факторы количества и цен, то в первую очередь определяется влияние количества, а потом уже цен.

Таким образом прежде чем приступить к расчетам необходимо:

1) выявить взаимосвязь между изучаемыми показателями;

2) разграничить количественные и качественные показатели;

3) определить последовательность подстановки.

Произвольное изменение последовательности подстановки будет менять количественную весомость того или иного показателя.

Источник

Тема 4. Метод детерменированного факторного анализа

4.1. Метод цепных подстановок

Метод цепных подстановок заключается в определении ряда промежуточных значений результативного показателя путем последовательной замены базисных значений факторов на отчетные. Данный способ основан на элиминировании. Элиминировать — значит устранить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Предполагается, что все факторы изменяются независимо друг от друга, т.е. сначала изменяется один фактор, а все остальные остаются без изменения, потом изменяются два при неизменности остальных и т.д.

В общем виде применение способа цепных постановок можно описать следующим образом:

где a₀, b₀, c₀ — базисные значения факторов, оказывающих влияние на обобщающий показатель у;
a₁ , b₁, c₁ — фактические значения факторов;
y_a, y_b, — промежуточные изменения результирующего показателя, связанного с изменением факторов а, b соответственно.

Общее изменение Δу = у₁ — у₀ складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов:

Рассмотрим пример. Исходные данные для факторного анализа сведены в таблицу 4.1. На основе этих данных проведем описанным выше способом анализ влияния на объем товарной продукции количества работников и их выработки.

Исходные данные для факторного анализа

Показатели	Услов. обозн-я	Базисные значения (0)	Фактические значения (1)	Изменение
				Абсолютное (+,- )	Относительное (%)
Объем товарной продукции, тыс. руб.	ТП	2920	3400	+480	116,40
Количество работников, чел	Ч	20	25	+5	125,00
Выработка на одного работающего, тыс. руб.	СВ	146	136	-10	93,15

Зависимость объема товарной продукции от данных факторов можно описать с помощью мультипликативной модели:

Тогда влияние изменения величины количества работников на обобщающий показатель можно рассчитать по формуле:

Далее определим влияние изменения выработки работников на обобщающий показатель:

Таким образом, на увеличение объема товарной продукции на 730 тыс. руб. положительное влияние оказало изменение на 5 человек численности работников. Отрицательное влияние оказало снижение выработки на 10 тыс. руб., что вызвало снижение объема на 250 тыс. руб. Суммарное влияние двух факторов привело к увеличению объема продукции на 480 тыс. руб.

Преимущества данного способа: универсальность применения, простота расчетов.

Недостаток метода состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения. Это связано с тем, что в результате применения этого метода образуется некий неразложимый остаток, который прибавляется к величине влияния последнего фактора. На практике точностью оценки факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора. Однако существуют определенные правила, определяющие последовательность подстановки:

• при наличии в факторной модели количественных и качественных показателей в первую очередь рассматривается изменение количественных факторов;
• если модель представлена несколькими количественными и качественными показателями, то в первую очередь определяется влияние факторов первого порядка, затем второго и т.д.

Под количественным факторами при анализе понимают те, которые выражают количественную определенность явлений и могут быть получены путем непосредственного учета (количество рабочих, станков, сырья и т.д.).

Качественные факторы определяют внутренние качества, признаки и особенности изучаемых явлений (производительность труда, качество продукции, средняя продолжительность рабочего дня и т.д.).

4.2. Метод абсолютных разниц

Метод абсолютных разниц является модификацией способа цепной подстановки. Изменение результативного показателя за счет каждого фактора определяется как произведение абсолютного прироста исследуемого фактора на базисную величину факторов, которые находятся справа от него и отчетную величину факторов, расположенных слева от него в модели.

4.3. Метод относительных разниц

Метод относительных разниц также является одной из модификацией способа цепной подстановки. Применяется для измерения влияния факторов на прирост результативного показателя в мультипликативных моделях. Он используется в случаях, когда исходные данные содержат определенные ранее относительные отклонения факторных показателей в процентах.

Для мультипликативных моделей типа у = а · в · с методика анализа следующая:

находят относительное отклонение каждого факторного показателя:

определяют отклонение результативного показателя у за счет каждого фактора

Пример. Воспользовавшись данными табл. 1, проведем анализ способом относительных разниц. Относительные отклонения рассматриваемых факторов составят:

Рассчитаем влияние на объем товарной продукции каждого фактора:

Результаты расчетов те же, что и при использовании предыдущего способа.

4.4. Интегральный метод

Интегральный метод применим к мультипликативным, кратным и смешанным моделям. Метод позволяет получать более точные результаты расчета влияния факторов по сравнению с методами цепной подстановки, абсолютных и относительных разниц. Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер, т. е. можно использовать также уже сформированные рабочие формулы, приводимые в специальной литературе:

4.5. Метод логарифмирования

Метод логарифмирования применяется для измерения влияния факторов только в мультипликативных моделях. Данный метод обеспечивает высокую точность расчетов. При этом результаты не зависят от местоположения факторов в модели. Дополнительный прирост от взаимодействия факторовраспределяется пропорционально доле изолированного влияния каждого фактора на уровень результативного показателя (пропорционально отношениям логарифмов факторных индексов к логарифму результативного показателя). При расчетах используются как натуральный, так и десятичный логарифм.

Рассмотрим возможность использования основных методов детерминированного анализа, обобщим вышеизложенное в виде матрицы (табл. 4.2).

Сферы применения способов детерминированного факторного анализа

Способы	Тип модели
	Мультипликативные	Аддитивные	Кратные	Смешанные
Цепной подстановки	+	+	+	+
Абсолютных разниц	+	—	+	—
Относительных разниц	+	—	—	у = а · (в — с)
Интегральный	+	—	+	у = a / Σвi
Логарифмический	+	—	—	—

Бальжинов А.В., Михеева Е.В. Анализ и диагностика финансово-хозяйственной деятельности предприятия: Учебн.пособ., — Улан-Удэ, 2003.

Источник