Способ цепных подстановок способ абсолютных отклонений

Метод цепных подстановок онлайн

Быстрая навигация по странице:

Общая характеристика метода цепных подстановок

Факторный анализ различных зависимостей достаточно широко применяется в практических расчетах. Наибольшей популярностью при проведении таких исследований пользуется метод цепных подстановок, что связано с его относительной простой и возможностью применения для анализа разных типов факторных моделей: мультипликативных, аддитивных, кратных, смешанных. Сущность рассматриваемого метода заключается в том, что в процессе подстановок производится последовательная замена значений факторов. При этом исходная таблица строится так, чтобы взаимосвязанные факторы всегда размещались по степени уменьшения их количественного влияния, т.е. сначала располагаются количественные показатели, а далее качественные (экстенсивные) факторы. В том случае, когда количественных (качественных) показателей несколько, то вначале размещаются наиболее общие из них. При практических вычислениях определяются некие условные значения результирующего показателя по следующему алгоритму: так, в первой подстановке выполняется замена значения базисного периода первого фактор на его величину в отчетном периоде. Вычитая из полученного условного значения показателя после первой замены его базисную величину, получаем размер влияния первого фактора, т.к. именно с этим фактором связано различие вычисленных величин показателей первой подстановки. Таким образом, приняв условие, что влияние других факторов, кроме первого, исключено (элиминировано), рассчитываем размер его влияния на показатель.

Размещено на www.rnz.ru

В следующей подстановке происходит замена следующего (второго) фактора, а именно его базисная величина заменяется на фактическую. Все прочие показатели берутся из предшествующей (первой) подстановки без замены. То есть, что первый фактор берется его фактической величиной, второй — так же фактической, остальные (если есть) — базисными. В результате полученное значение скорректированного показателя после второй замены будет отличаться от предыдущего только вторым фактором. Для исчисления величины его влияния на показатель требуется от суммы показателя второй подстановки отнять значение показателя первой подстановки. Дальнейшие расчеты производятся по такому же алгоритму. Количество подстановок всегда будет на единицу меньше количества факторов, т.к. в последней подстановке используются все фактические (отчетные) величины показателей. Для расчета величины влияния последнего фактора в моделях с любым их числом требуется от фактического (отчетного) значения итогового показателя отнять величину, полученную при расчете последней подстановки.

Сумма величин влияния всех факторов должна совпадать с величиной общего изменения итогового показателя. Если этого равенства не получается, то необходимо найти ошибку в вычислениях. Существенным условием правильности применения рассматриваемого метода цепных подстановок является соблюдение правила: каждая рядом стоящая замена должна отличаться только одним фактором, величина влияния которого и рассчитывается.

Формула метода цепных подстановок

Формула метода цепных постановок будет зависеть от количества факторов, из которых построена модель анализируемого показателя. Например, для двух факторов и мультипликативной модели применение рассматриваемого метода будет опираться на следующую систему формул:

Формула метода цепных подстановок

Пример анализа методом цепных подстановок

В качестве примера рассмотрим факторный анализ продаж. В общем случае объем продаж предприятия зависит от цены, по которой осуществлялась продажа товаров и от количества проданных товаров. Тогда факторную модель для анализа продаж можно записать следующим образом (мультипликативная модель): W = Q * P, где W — выручка (объем продаж), P — цена единицы товара, Q — количество проданных единиц товара. Таблица исходных данных будет следующая:

Показатель	По плану	Фактически
Продано продукции, шт.	2000	2500
Цена продажи единицы продукции, руб.	5.5	6.2
Объем продаж, руб.	11000	15500

Выполним необходимые расчеты:

W₀ = 2000 * 5.5 = 11000 руб.

W_усл1 = 2500 * 5.5 = 13750 руб.

W₁ = 2500 * 6.2 = 15500 руб.

ΔW_Q = 13750 — 11000 = 2750 руб.

ΔW_P = 15500 — 13750 = 1750 руб.

Проверка: 2750 + 1750 = 4500 = 4500 руб., результаты расчетов совпадают.

Вывод: анализ полученных результатов показывает, что в целом объем продаж увеличился на 4500 руб. Данное изменение произошло под влиянием следующих причин: за счет роста количества проданной продукции на 500 шт. объем продаж увеличился на 2750 руб. За счет роста цены продажи единицы продукции на 0.7 руб. объем продаж увеличился на 1750 руб.

Онлайн-калькулятор метода цепных подстановок

Для проведения факторного анализа методом цепных подстановок приводим простую форму онлайн-калькулятора, используя который, Вы можете самостоятельно выполнить расчет данных показателей и заполнить таблицу. Для получения правильных результатов работы онлайн-калькулятора в процессе ввода данных необходимо внимательно соблюдать размерность полей, что позволит выполнить необходимые вычисления быстро и точно. Дробные величины должны вводиться с ТОЧКОЙ, а не с запятой! В представленной форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как работает факторный анализ способом цепных подстановок онлайн. Для проведения анализа по своим данным просто внесите их в соответствующие поля формы онлайн-калькулятора и нажмите кнопку «Выполнить расчет».

Источник

Метод цепных подстановок

Способ цепных подстановок может быть использован во всех типах детерминированных факторных моделей (аддитивные, мультипликативные, кратные, комбинированные) для расчёта величины влияния фактора на результат.

Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью рассчитывают ряд условных величин, которые учитывают изменение одного, двух и т.д. факторов, допуская, что остальные факторы не меняются. Сравнение величины результата до и после изменения уровня того или иного фактора позволяют элиминироваться от влияний всех факторов, кроме одного.

Алгоритм метода цепных подстановок для многофакторной мультипликативной модели

1. Рассчитываем плановый показатель: Y0 = a0 * b0 * с0* d0;

2. Далее рассчитывается система условных показателей:
Y_усл.1 = a1 * b0 * с0* d0;
Y_усл.2 = a1 * b1 * с0* d0;
Y_усл.3 = a1 * b1 * с1* d0;

3. Рассчитываем фактический показатель: Y1 = a1 * b1 * с1* d1;

4. Путем последовательного вычитания полученных показателей находим изменение результативного показателя за счет факторов:
ΔYа = Y_усл.1 – Y0;
ΔYb = Y_усл.2 – Y_усл.1;
ΔYс = Y_усл.3 – Y_усл.2;
ΔYd = Y1– Y_усл.3;
5. Рассчитываем общее отклонение фактического показателя от планового, которое равно сумме факторных отклонений:
ΔY = Y1 — Y0 = ΔYа + ΔYb + ΔYс + ΔYd

Рекомендации при использовании этого метода:
А) в первую очередь учитываются изменения количественных показателей, затем качественные;
Б) сначала учитываются факторы первого уровня подчинения, затем второго и т.д.

Пример . Исходные данные для расчета влияния факторов базисные: (y0 = 1,58; a0 = 12940; b0 = 8210 ) и фактические: (y1 = 1,53; a1 = 13950; b1 = 9124; ). Рассчитайте влияние на отклонение результативного показателя (y) каждого из определяющих его факторов (a, b).

Источник

Метод цепных подстановок и абсолютных разниц

Метод цепных подстановок является одним из базовых методов экономического анализа, который применяется для анализа мультипликативных моделей. При этом каждый фактор последовательно изменяется с базисного на отчетное значение, тогда как остальные остаются без изменения.

Можно проводить расчеты в таблице. Предположим, что анализируемый показатель «А» представляет собой произведение трех факторов (Ф1, Ф2, Ф3).

Абсолютное изменение показателя известно. Необходимо определить суммы факторного влияния – насколько изменился результирующий показатель под влиянием изменения конкретного фактора. Размер факторного влияния Аф1, Аф2, Аф3 будет определяться следующим образом:

Фактор 1	Фактор 2	Фактор 3	Анализируемый показатель	Размер влияния на анализируемый показатель
Базисный	Базисный	Базисный	Базисный (Б)
Отчетный	Базисный	Базисный	Условный 1 (У1)	Аф1 = У 1 – Б
Отчетный	Отчетный	Базисный	Условный 2 (У2)	Аф2 = У 2 – У 1
Отчетный	Отчетный	Отчетный	Отчетный (О)	Аф3 = О – У 2

Общая сумма факторных отклонений дает абсолютное отклонение (изменение) показателя. Достоинством приема является то, что количество факторов не имеет значения и не влияет на методику расчета, увеличивается только количество «шагов» расчета.

Для примера представим выручку условного транспортного предприятия как произведение следующих факторов – количество машин, количество рейсов одной машины, количество пассажиров за одну поездку и стоимость проезда одного пассажира:

Данные о значении факторов в базисном и отчетном периоде представлены в таблице 7.

Показатель	Обозначение	Базисный период	Отчетный период
Количество машин	М
Количество рейсов	Р
Количество пассажиров	П
Стоимость проезда	С
Выручка	В

Абсолютное отклонение выручки составит + 180000 р.

Рассчитаем факторные отклонения. Если все факторы будут иметь базисное значение, сумма выручки составляет 1500000 р.

Затем мы будем постепенно заменять значения факторов с базисного значения на отчетное:

В базис = 25*10*40*150 =1500000

В усл 1 = 30*10*40*150 = 1800000

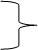
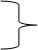
1440000 – 1800000 = — 360000.

В усл 2 = 30*8*40*150 = 1440000

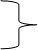
1260000 – 1440000 = — 180000.

В усл 3 = 30*8*35*150 = 1260000

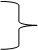
1680000 – 1260000 = + 420000.

В отчет = 30*8*35*200 = 1680000

По итогам расчетов можно сделать вывод, что за счет увеличения количества машин предприятие получило дополнительную выручку в сумме 300000 рублей, а за счет увеличения тарифа – в сумме 420000 рублей. В то же время сказалось отрицательное влияние таких факторов, как уменьшение количества рейсов одной машины и уменьшение количества пассажиров на каждом рейсе (недополучено выручки на сумму360000 и 180000 рублей соответственно).

Прием цепных подстановок считается основным приемом факторного анализа, но имеет существенный недостаток – наличие так называемого «неразложимого остатка». Это означает, что при изменении порядка факторов в модели изменяется сумма факторных отклонений. Поэтому при составлении моделей для проведения факторного анализа существует следующее правило – сначала указываются количественные, а затем стоимостные показатели. Если необходимо обеспечить высокую точность расчетов, используются логарифмический или интегральный прием.

Метод абсолютных разниц является разновидностью приема цепных подстановок. Каждый фактор последовательно представляется в виде разницы между отчетным и базисным значениями. Остальные показатели принимаются в отчетном или базисном значении в зависимости от расположения в формуле (соответственно до анализируемого фактора или после него).

Аф1 = (Ф1о – Ф1б) * Ф2б * Ф3б;

Аф2 = Ф1о * (Ф2о – Ф2б) * Ф3б;

Аф3 = Ф1о * Ф2о * (Ф3о-Ф3б),

где Ф1б, Ф2б, Ф3б – факторы в своем базисном значении;

Ф1о, Ф2о, Ф3о – факторы в своем отчетном значении.

Вопросы для обсуждения:

1. Почему метод абсолютных разниц считается разновидностью метода цепных подстановок? Какой из предложенных приемов факторного анализа проще применять и почему?

2. Можно ли представить модель, предложенную в примере, как произведение большего количества факторов? Как произведение меньшего количества факторов?

Задачи и ситуации:

1. Рассчитать показатели рентабельности продукции и капитала по данным условного предприятия и определить, используя формулу Дюпона, влияние на изменение рентабельности активов изменения рентабельности продукции и оборачиваемости активов. Аналогичные расчеты провести по рентабельности собственного капитала.

Показатель	Прошлый год	Отчетный год
Выручка
Валюта баланса
Прибыль до налогообложения
Собственный капитал

2. Рассчитать при помощи приема абсолютных разниц:

Влияние на суммарные материальные затраты изменений в стоимости сырья и нормы расхода сырья на производство продукции.

Показатели	Прошлый год	Отчетный год
Стоимость 1 кг сырья
Норма расхода, кг
Материальные затраты	?	?

Определить разницу в значении факторных отклонений при изменении места расположения показателей — факторов.

3. Составить мультипликативную модель и определить факторное влияние на изменение товарооборота следующих факторов:

— средняя стоимость товара;

— количество работников торгового зала;

— количество проданных товаров на одного работника.

Источник