Глава 11. Метрические задачи
Глава 11
§ 73. Развертки пирамидальных и конических поверхностей
Развертки пирамидальных и конических поверхностей строят способом триангуляции (способом треугольников). Построение разверток этих поверхностей сводится к многократному построению истинных величин треугольников, из которых состоит поверхность развертываемой пирамиды или которой заменяют развертываемую коническую поверхность.
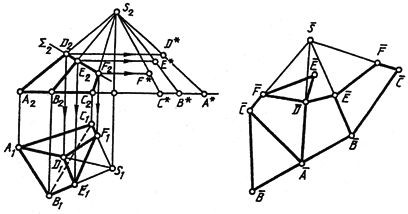
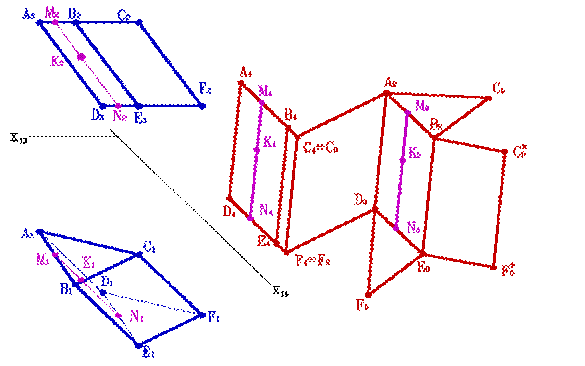
На рис. 148 построена полная развертка пирамиды SABC, усеченной фронтально проецирующей плоскостью Σ(Σ2).
Сначала нужно построить развертку боковой поверхности всей пирамиды (фигуру S С А В С), состоящую из натуральных величин боковых граней. Для этого необходимо определить истинную величину боковых ребер. На рис. 148 истинная величина ребер AS, BS, CS построена способом прямоугольного треугольника. В данном случае одним катетом взято превышение точки S над точками А, В и С, а вторым катетом — горизонтальная проекция соответствующего ребра. Гипотенузы S2C*, S2B* и дают истинную величину боковых ребер. Основание пирамиды расположено горизонтально, поэтому на плоскости П1 имеем истинную величину и самого основания ∆АВС, и его сторон АВ, ВС, АС.
Каждая боковая грань на развертке строится как треугольник по трем сторонам. CS — самое короткое боковое ребро, поэтому рациональнее мысленно разрезать пирамиду по этому ребру.
Для нанесения на развертку точек D, E и F, соответствующих вершинам сечения пирамиды плоскостью Σ, нужно определить истинные расстояния этих точек от вершины S. После построения развертки боковой грани поверхности усеченной части пирамиды нужно пристроить к ней треугольники A B C и D E F, дающие истинную величину основания и сечения пирамиды.
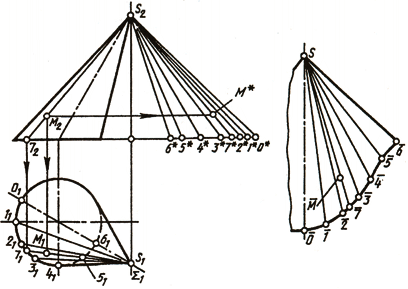
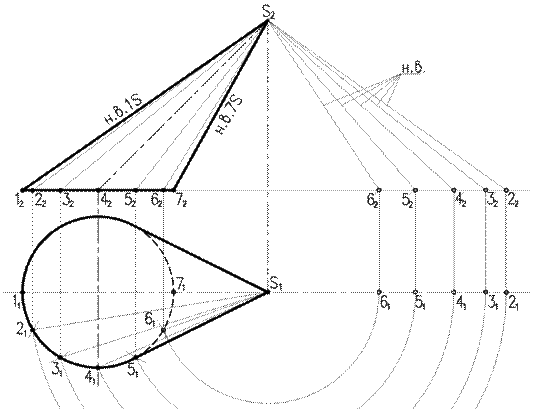
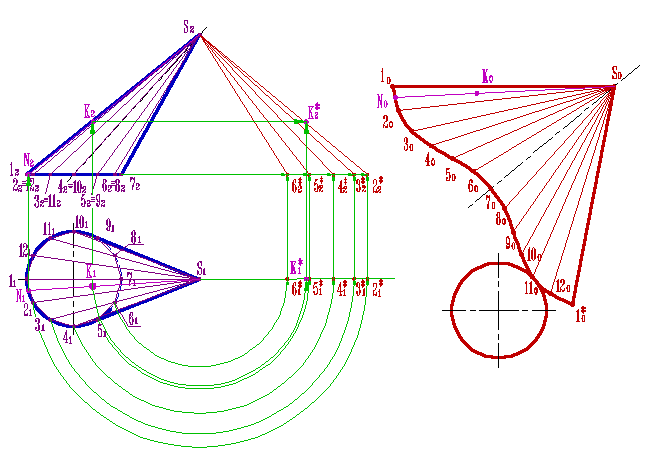
На рис. 149 способом триангуляции построена развертка конической поверхности, которая заменена поверхностью вписанной в нее двенадцатиугольной пирамиды. Развертка представляет собой симметричную фигуру, так как поверхность имеет плоскость симметрии Σ. В этой плоскости лежит самая короткая образующая S-6. По ней и сделан разрез поверхности. Самая длинная образующая S-0 является осью симметрии развертки поверхности.
Натуральные величины образующих определены с помощью прямоугольных треугольников, как в предыдущей задаче на рис. 149. От оси симметрии S-0 строим шесть в одну сторону и шесть в другую сторону примыкающих друг к другу треугольников с общей вершиной S. Каждый из треугольников строим по трем сторонам, при этом две стороны равны истинным величинам образующих, а третья хорде, стягивающей дугу окружности основания между соседними точками деления. Построенные на развертке точки 0, 1, 2, . соединяются.
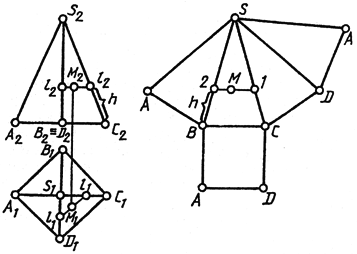
Построение развертки значительно упрощается, если поверхность представлена прямой пирамидой правильной формы или прямым круговым конусом. На рис. 150 приведена развертка четырехгранной прямой пирамиды.
Построение ее упрощается тем, что образующие пирамиды AS и CS параллельны фронтальной плоскости проекций и на нее спроецировались в натуральную величину. Основание же пирамиды ABCD лежит в плоскости, параллельной горизонтальной плоскости проекций, и на нее проецируется в натуральную величину. Для построения развертки достаточно построить стороны AS и сделать засечки радиусом дуги, равным BS и АВ из точек S и А соответственно, получим точку В и т. д. Основание же в натуральную величину можно построить на базе одной из его сторон (на рис. 150 — на базе стороны АВ). Положение точки на поверхности развертки пирамиды определим в следующем порядке: через фронтальную проекцию точки М (М2) проведем горизонтальную линию до пересечения с ребрами А2S2 и B2S2. Получим точки 11 и 22. На линии AS развертки от точки А отложим отрезок h и из полученной точки 1 проведем линию 1, 2 параллельно AD, на которой нанесем точку М в том положении, которое она занимает на горизонтальной проекции линии 1, 2.
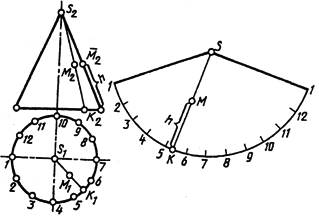
На рис. 151 приведен пример построения развертки прямого кругового конуса. Для построения ее используем то, что очерковая образующая конуса l на фронтальной плоскости изобразилась в натуральную величину. Выбрав положение вершины развертки — точку S, радиусом L проводим дугу и откладываем на ней 12 равных частей, на которые предварительно разделили окружность основания конуса, изображенного на горизонтальной плоскости проекции в натуральную величину. Чем на большее количество равных участков разделим окружность, тем точнее построим развертку.
Положение точки М на развертке поверхности конуса определим следующим образом: через фронтальную проекцию точки проведем образующую и построим горизонтальную ее проекцию. Найдем, что образующая пересекла основание конуса между точками 5 и 6. Точку К переносим на дугу развертки, расположив ее между точками 5 и 6, и соединим с вершиной конуса развертки S. Из точки М2 проведем горизонтальную линию до пересечения с очерковой образующей L и получим точку М2. Расстояние от основания конуса до точки М2 по образующей является высотой точки, которую откладываем на развертке от точки К на линии KS. Полученная точка определит истинное положение точки М на развертке.
Таким образом, развертку конической поверхности построим с помощью соседних точек окружности основания, в которую вписан правильный двенадцатиугольник, т. е. коническая поверхность условно заменена поверхностью, вписанной правильной двенадцатиугольной пирамидой, а для построения развертки применен способ триангуляции.
© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения
Источник
Способ триангуляции
Построение разверток развертываемых поверхностей
Общие сведения
Лекция 3. Построение разверток поверхностей. Аксонометрия
· Построение разверток поверхностей способом триангуляции.
· Построение разверток поверхностей способом раскатки.
· Общие сведения об аксонометрии.
· Стандартные виды аксонометрических проекций.
Разверткой поверхностиназывается плоская фигура, полученная путем совмещения элементов поверхности с плоскостью.
Если для поверхности можно построить её развертку точно без складок и разрывов, то поверхность называется развертываемой, в противном случае – неразвертываемой.
К развертываемым поверхностям относятся все гранные, а из линейчатых только – цилиндрические, конические и поверхности с ребром возврата.
Существуют следующие способы построения разверток развертываемых поверхностей:
1. Способ триангуляции (треугольников);
2. Способ раскатки;
3. Способ нормального сечения.
Способ триангуляции (треугольников)применяется для построения разверток пирамидальных и конических поверхностей. Они выполняются по одному принципу. Каждая грань пирамиды представляет треугольник и для построения развертки необходимо определить натуральные величины всех сторон треугольника. По найденным натуральным величинам сторон вычерчиваются последовательно треугольные грани. Коническая поверхность, заменяется вписанной в нее, пирамидальной и решение задачи ведется аналогично пирамиде.
Рассмотрим пример, построения развертки, конической поверхности (рисунок 3.1)
Для построения развертки в конус вписываем двенадцатигранную пирамиду. Т.к. по условию конус расположен симметрично относительно оси, построим половину развертки.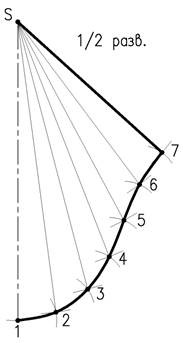 
Образующие конуса имеют разную длину, поэтому натуральную величину определяем вращением до положения параллельного фронтальной плоскости проекций. Только образующие S1 и S7, проецируются в натуральную величину. По полученным натуральным величинам образующих и размерам хорд окружности основания, между образующими, строим половину развертки, состоящую из шести треугольников вписанной в конус пирамиды. Точки основания соединяем плавной кривой линией.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Способ триангуляции (треугольников)
Способ триангуляции (треугольников) применяется для построения разверток пирамидальных, конических и других линейчатых поверхностей, кроме цилиндрических.
Сущность способа сводится к многократному построению натурального вида треугольников, из которых состоит данная пирамидальная поверхность или многогранная поверхность, вписанная (или описанная) в данную коническую или линейчатую поверхность и заменяющая ее.
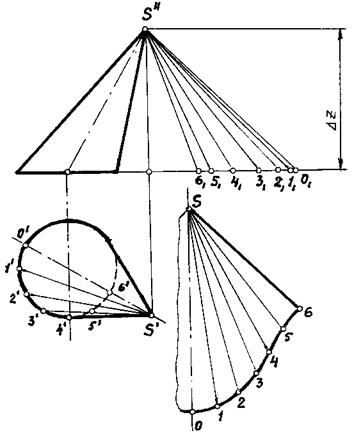
Пример. Построить развертку боковой поверхности эллиптического конуса с круговым основанием (рис. 166).
В данном примере коническая поверхность заменяется поверхностью вписанной двенадцатиугольной пирамиды. Так как коническая поверхность имеет плоскость симметрии, то можно построить развертку только одной половины поверхности. Разделив от точки О половину окружности основания конической поверхности на шесть равных частей и определив с помощью прямоугольных треугольников натуральные величины образующих, проведенных в точки деления, строим шесть примыкающих один к другому треугольников с общей вершиной S (рис. 166). Каждый из этих треугольников строится по трем сторонам; при этом две стороны равны натуральным величинам образующих, а третья — хорде, стягивающей дугу окружности основания между соседними точками деления. После этого через точки 0,1,2. разогнутого по способу хорд основания конической поверхности проводится плавная кривая (рис. 166).
Источник
Способ триангуляции
Способ триангуляции или способ вспомогательных треугольников применяют для построения приближенной развертки неразвертываемых поверхностей.
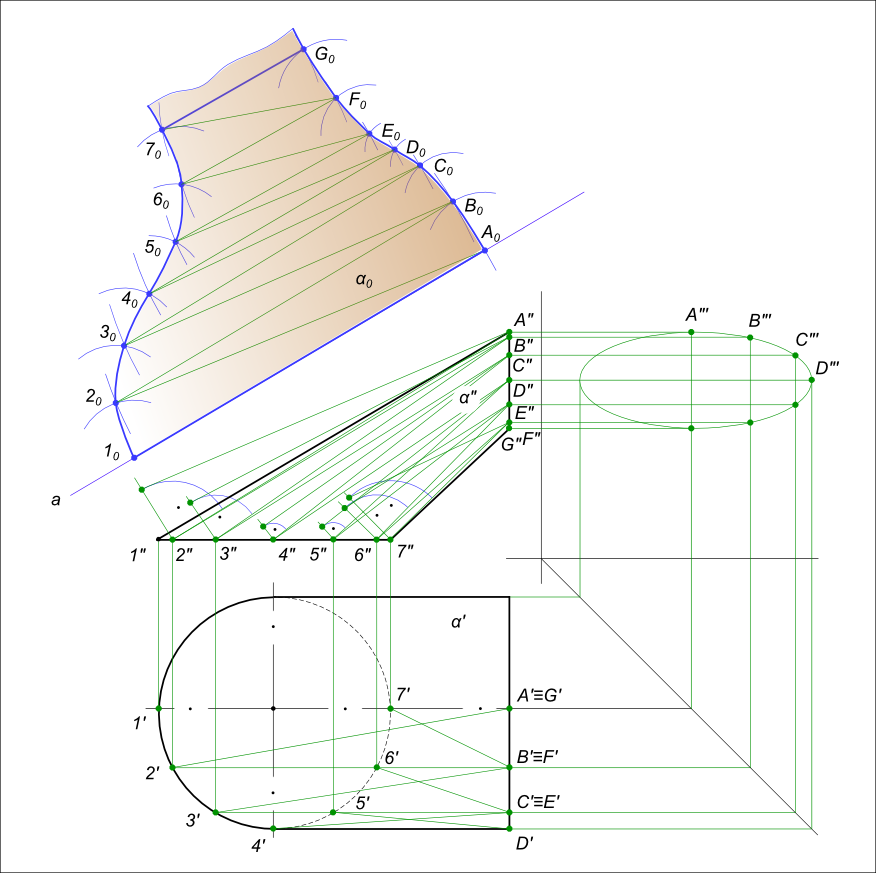
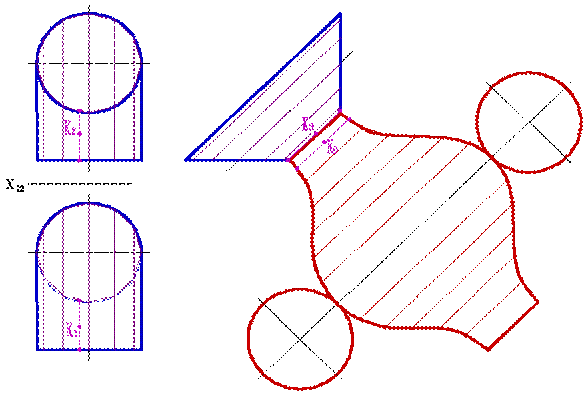
Дан цилиндроид α, сопрягающий две трубы одна круглого сечения другая эллиптического, причем диаметр круглой равен диаметру большой оси эллипса.
У цилиндроида поверхность неразвертываемая. Поэтому применяем способ триангуляции — аппроксимируем ее вписанной многогранной поверхностью состоящей из треугольников. На поверхности цилиндроида проводим ряд прямолинейных образующих, параллельных плоскости параллелизма: — 1A, 2B, 3C, 4D, 5E, 6F и 7G. Здесь плоскостью параллелизма выступает фронтальная плоскость проекции. Участок поверхности между смежными образующими 1A и 2B разделим диагонально 2A на два участка, которые считаем треугольниками. Таким же образом разделим на элементарные треугольники все остальные участки находящиеся между образующими.
Выполняем построение развертки многогранной поверхности состоящей из элементарных треугольников: — проводим на свободном месте чертежа произвольную прямую a; — откладываем на ней первую образующую [10A0] ≅ [1″A»]; — проводим дуги радиусом [1`2`] и радиусом |A`2`|, на их пересечении находим точку 20. Натуральную величину [A2] определяем способом прямоугольного треугольника; — соединяем точки A0 и 20 прямой линией; — из точки 20 строим вторую образующую [20B0] ≅ [2″B»]; — проводим дуги радиусом [2″B»] и радиусом [A»`B»`],на их пересечении находим точку B0; — соединяем точки 20 и B0 прямой линией. Аналогично строим другие точки развертки, которые соединяем плавной кривой. На рисунке показано построение половины развертки потому, что вторая половина ей симметрична.
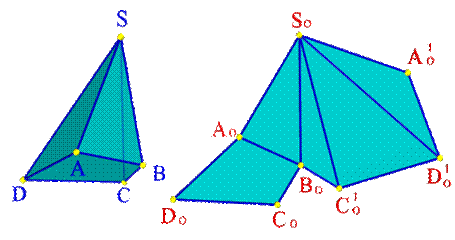
Способ триангуляции применяют для построения развертки поверхности пирамиды: Способ треугольников.
Способ триангуляции или способ треугольников использован для построения развертки поверхности усеченной пирамиды в графической работе №12: Графическая работа 12
Источник
Развертка поверхности. Способы построения разверток
Цель лекции: изучение свойств развертки и способов построения разверток многогранников и поверхностей вращения
· Развертка поверхностей. Общие понятия.
· Способы построения разверток: методы триангуляции, нормального сечения и раскатки.
· Построение разверток гранных поверхностей и поверхностей вращения.
Развертка поверхностей. Общие понятия
| Развертка | плоская фигура, полученная при совмещении поверхности геометрического тела с плоскостью (без наложения граней или иных элементов поверхности друг на друга). Развертку можно рассматривать как гибкую, нерастяжимую пленку. Некоторые из представленных таким образом поверхностей можно путем изгибания совместить с плоскостью. При этом, если отсек поверхности может быть совмещен с плоскостью без разрывов и склеивания, то такую поверхность называют развертывающейся, а полученную плоскую фигуру – ее разверткой. |
| Основные свойства развертки | 1 Длины двух соответствующих линий поверхности и ее развертки равны между собой; 2 Угол между линиями на поверхности равен углу между соответствующими им линиями на развертке; 3 Прямой на поверхности соответствует также прямая на развертке; 4 Параллельным прямым на поверхности соответствуют также параллельные прямые на развертке; 5 Если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая на развертке, то эта линия является геодезической. |
Методы триангуляции, нормального сечения и раскатки
Построение разверток гранных поверхностей и поверхностей вращения
| Существует три способа построения развертки многогранных поверхностей: | ||
| 1-й способ | 2-й способ | 3-й способ |
| Способ триангуляции (треугольника) | Способ нормального сечения | Способ раскатки |
а) Развертка поверхности многогранника.
Разверткой многогранной поверхности называется плоская фигура, получаемая последовательным совмещением всех граней поверхности с плоскостью.
Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины отдельных граней поверхности – плоских многоугольников.
Метод триангуляции
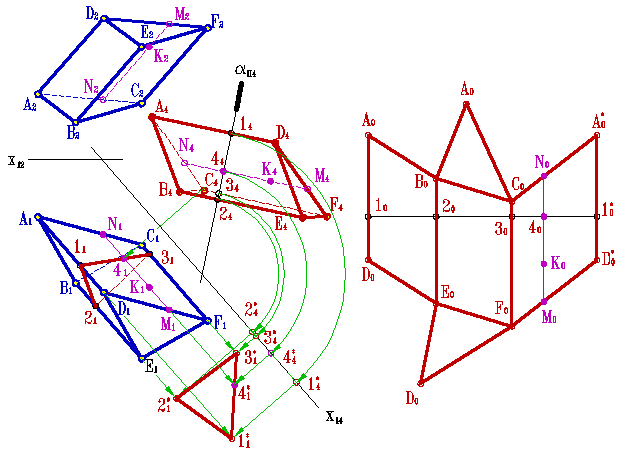
Пример 1. Развертка пирамиды (рисунок 13.1).
При построении развертки пирамиды применяется способ треугольника. Развертка боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников – граней пирамиды и многоугольника — основания. Поэтому построение развертки пирамиды сводится к определению натуральной величины основания и граней пирамиды. Грани пирамиды можно построить по трем сторонам треугольников, их образующих.
Рисунок 13.1. Пирамида и её развертка
Для этого необходимо знать натуральную величину ребер и сторон основания. Алгоритм построения можно сформулировать следующим образом (рисунок 13.2):
| 1 Определяют натуральную величину основания пирамиды (например, методом замены плоскостей проекций) |
| 2 Определяют истинную величину всех ребер пирамиды любым из известных способов (в данном примере натуральная величина всех ребер пирамиды определена методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций и проходящей через вершину пирамиды S) |
| 3 Строят основание пирамиды и по найденным трем сторонам строят какую-либо из боковых граней, пристраивая к ней следующие (рисунок 13.3). |
Рисунок 13.2. Определение истинной величины
основания и ребер пирамиды
Точки, расположенные внутри контура развертки, находят во взаимно однозначном соответствии с точками поверхности многогранника. Но каждой точке тех ребер, по которым многогранник разрезан, на развертке соответствуют две точки, принадлежащие контуру развертки. Примером первой точки на рисунках служит точка К0 и КÎSАD, а иллюстрацией второго случая являются точки М0 и М0 * . Для определения точки К0 на развертке пришлось по ее ортогональным проекциям найти длины отрезков АМ (метод замены плоскостей проекций) и SК (метод вращения). Эти отрезки были использованы затем при построении на развертке сначала прямой S0М0 и, наконец, точки К0.
Рисунок 13.3. Построение развертки пирамиды
Способ нормального сечения
В общем случае развертка призмы выполняется следующим образом. Преобразуют эпюр так, чтобы ребра призмы стали параллельны новой плоскости проекций. Тогда на эту плоскость ребра проецируются в натуральную величину.
Пример 2. Развертка призмы (рисунок 13.4).
Пересекая призму вспомогательной плоскостью α, перпендикулярной ее боковым ребрам (способ нормального сечения), строят проекции фигуры нормального сечения – треугольника 1, 2, 3, а затем определяют истинную величину этого сечения. На примере она найдена методом вращения.
В дальнейшем строям отрезок 10-10 * , равный периметру нормального сечения. Через точки 10, 20, 30 и 10 * проводят прямые, перпендикулярные 10-10 * , на которых откладывают соответствующие отрезки боковых ребер призмы, беря их с новой фронтальной проекции. Так, на перпендикуляре, проходящем через точку 10, отложены отрезки 10D0=14D4 и 10А0=14А4.. Соединив концы отложенных отрезков, получают развертку боковой поверхности призмы. Затем достраивают основание.
Способ раскатки
Пример 3. Развертка призмы, частный случай, когда основание призмы на одну из плоскостей проекций проецируется в натуральную величину (рисунок 13.5).
Развертка боковой поверхности такой призмы осуществляется способом раскатки. Этот способ заключается в следующем. Сначала, как и в предыдущем примере, преобразуют эпюр так, чтобы боковые ребра призмы стали параллельны одной из плоскостей проекций.
Рисунок 13.4. Развертка призмы способом нормального сечения
Рисунок 13.5. Развертка призмы способом раскатки
Затем новую проекцию призмы вращают вокруг ребра С4F4 до тех пор пока грань ACDF не станет параллельной плоскости П4.
При этом положение ребра С4F4 остается неизменным, а точки принадлежащие ребру AD перемещаются по окружностям, радиус которых определяется натуральной величиной отрезков AC и DF (так как основания призмы параллельны П1 то на эту плоскость проекций они проецируются без искажения, т.е. R=A1C1=D1F1), расположенных в плоскостях, перпендикулярных ребру С4F4.
Таким образом, траектории движения точек A и D на плоскость П4 проецируются в прямые, перпендикулярные ребру С4F4.
Когда грань ACDFстанет параллельна плоскости П4, она проецируется на неё без искажения т.е. вершины A и D окажутся удаленными от неподвижных вершин C и F на расстояние, равное натуральной величине отрезков AC и DF. Таким образом, засекая перпендикуляры, по которым перемещаются точки A4 и D4 дугой радиуса R=A1C1=D1F1, можно получить искомое положение точек развертки A0 и D0.
Следующую грань АBDE вращают вокруг ребра AD. На перпендикулярах, по которым перемещаются точки B4и E4 делают засечки из точек A0 и D0 дугой радиуса R=A1B1=D1E1. Аналогично строится развертка последней боковой грани призмы.
Процесс последовательного нахождения граней призмы вращением вокруг ребер можно представить как раскатку призмы на плоскость параллельную П4 и проходящую через ребро С4F4.
Построение на развертке точки К, принадлежащей боковой грани АBDE, ясно из рисунка. Предварительно через эту точку по грани провели прямую NМ, параллельную боковым ребрам, которая затем построена на развертке.
б) Развертка цилиндрической поверхности.
Развертка цилиндрической поверхности выполняется аналогично развертке призмы. Предварительно в заданный цилиндр вписывают n-угольную призму (рисунок 13.6). Чем больше углов в призме, тем точнее развертка (при n →призма преобразуется в цилиндр).
в) Развертка конической поверхности
Развертка конической поверхности выполняется аналогично развертке пирамиды, предварительно вписав в конус n-угольную пирамиду (рисунок 13.6).
Если задана поверхность прямого конуса, то развертка его боковой поверхности представляет круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ=360 о r / l, где r – радиус окружности основания конуса.
Рисунок 13.6. Развертка цилиндрической поверхности
Рисунок 13.7. Развертка конической поверхности
| Запомните! Задание | Существует три способа построения развертки: способ нормального сечения, раскатки и треугольника.Дайтехарактеристику каждому из способов. Внимательно рассмотрите примеры, приведенные в лекции. Выполните построения по рисункам 13.1…13.7. |
Контрольные вопросы
1 Что называют разверткой поверхности?
2 Какие поверхности называют развертывающимися и какие – неразвертывающимися?
3 Укажите основные свойства разверток
4 Укажите последовательность графических построений разверток поверхностей конуса и цилиндра.
5 Какие способы построения разверток многогранников вы знаете?
Источник
