Способ триангуляции для определения горизонтальных смещений

Другие методы определения горизонтальных смещений

При большом уклонении наблюдаемых точек от створа, больших разностях их высот или при расположении точек в различных местах сооружения величины горизонтальных смещений необходимо знать по двум координатам. В таких случаях применяют линейно-угловые построения. Эти построения могут развиваться в виде специальных сетей триангуляции и трилатерации, комбинированных сетей, угловых и линейных засечек, ходов полигонометрии, сетей вытянутых треугольников с измеренными сторонами и высотами. Выбор того или иного построения зависит от характера сооружения и его геометрической формы, требуемой точности и условий измерений, организационных и других факторов. Так, например, угловую и линейную засечки применяют для определения смещений недоступных точек сооружения; триангуляцию, полигонометрию и сети вытянутых треугольников – для протяженных объектов криволинейной формы. Во многих случаях применяют комбинированные схемы, когда, например, триангуляция и трилатерация используется для определения устойчивости исходных пунктов, с которых способами засечек или полигонометрии определяют смещения точек на сооружении.

Применительно к измерениям деформаций каждый из видов линейно-угловых построений обладает своими особенностями. Однако для всех видов характерным является постоянство схемы измерений необходимость получения в конечном итоге не самих координат деформационных точек, а их изменений во времени, т.е. разностей координат в двух циклах.

Триангуляционный метод включает способы собственно триангуляции, трилатерации, направлений, прямых и обратных угловых, комбинированных и линейных засечек [49].

Для исследования горизонтальных смещений линейно-угло­вые построения могут развиваться в виде специальных сетей триангуляции и трилатерации, комбинированных сетей, угло­вых и линейных засечек, ходов полигонометрии (см. рис.8.10) Применение того или иного вида построения зависит от характера соору­жения, его геометрической формы, требуемой точности и усло­вий измерений, организационных и других факторов. Напри­мер, угловую или линейную засечку применяют для определе­ния смещений недоступных точек сооружения, а триангуляцию и полигонометрию — для протяженных сооружений криволиней­ной формы. Во многих случаях применяют комбинированные схемы, в которых триангуляция или трилатерация используют для определения исходных пунктов и временных координат вспомогательных точек, с которых методом засечек или полигонометрии определяют смещения точек на сооружении.

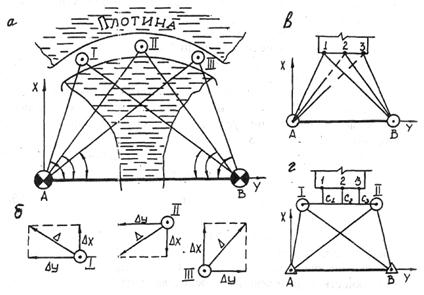
Рис.8.10. Схема наблюдений за горизонтальными смещениями:

а — метод триангуляции; б — схема смещения наблюдательных столбов;

в — метод отдельных направлений; г -комбинированный метод

Применительно к измерениям деформаций каждый из ви­дов линейно-угловых построений обладает рядом специфиче­ских особенностей. Однако для всех видов характерным явля­ется постоянство схемы измерений и необходимость получения в конечном итоге не самих координат деформационных точек, а их изменений во времени, т. е. разностей координат в т-ом и k-ом циклах.

Теория линейно-угловых сетей достаточно хорошо изучена, и преимущества их перед другими видами геодезических по­строений общеизвестны.

Метод триангуляции и угловых засечек следует применять для измерения горизонтальных перемещений фундаментов зданий и сооружений, возводимых в пересеченной или горной местности, а также при невозможности обеспечить устойчивость концевых опорных знаков створа. Этот метод нашел широкое применение при наблюдениях за бетонными арочными плотинами.

Производят высокоточные угловые измерения способом круговых приемов теодолитами Т1, Т2.

Допускается применять ус­ловную систему координат. В этом случае оси координат X и У должны совпадать с поперечной и продольной осями здания или сооружения.

Измерение горизонтальных углов необходимо выполнять с погрешностью, не превышающей приведенной в табл. 8.2.

Класс точности измерений	Допускаемая средняя квадратическая погрешность измерения углов, угл.с, для расстояний, м
I
II
III
IV

Величину и направление горизонтального перемещения фундамента (или его части) следует определять по изменениям координат деформационных марок за промежуток времени между циклами наблюдений по формулам

, (8.24)

где — значения координат в i-ом цикле наблюдений, — значения координат в нулевом цикле наблюдений.

Величина горизонтального перемещения вычисляется по формуле

(8.25)

Средняя квадратическая погрешность определения горизонтального смещения вычисляется по формуле

, (8.26)

где — погрешности определения смещений по осям координат Х и У.

Метод триангуляции трудоемок, но дает высокую точность, поэтому чаще всего он применяется при строительстве и эксплуатации крупных прецизионных сооружений.

В каждом цикле наблюдений относительно опорных пунктов А и В методом триангуляции (рис.8.10,а) определяют координаты наблюдательных столбов I, II, III, закрепленных на сооружении (например плотине). По разности координат вычисляют гори­зонтальное смещение столбов I, II, III по направлениям осей X и У. Длину базиса АВ измеряют с высокой точностью светодальномером.

Величину общего смещения вычисляют как диагональ прямо­угольника (рис.8.10,б) со сторонами Х и У.

При наблюдениях за смещением наблюдаемых точек методом отдельных направлений (рис.8.10,в) выполняют повторные измерения горизонтальных углов в опорных пунктах А и В, акоординаты точек 1,2 и 3 вычисляют угловыми засечками.

При отклонении направлений А1 и Bl, A2 и т.д. от здания до 8° погрешность в определении смещения не будет превышать 1:100 её зна­чения.

Метод полигонометрии используется в стесненных условиях в строительный период для изучения смещений тоннелей, кольцевых сооружений и арочных плотин.

Для измерения углов используют высокоточные теодолиты, для измерения расстояний – светодальномеры. Количество приемов при наблюдениях рассчитывают для каждого случая.

Если ход полигонометрии прокладывают внутри сооружения, то отсутствует возможность азимутальной привязки хода. В этом случае при уравнивании результатов наблюдений используют только координатные условия. Если ход прокладывают снаружи (например, по гребню плотины), то при этом измеряют примычные углы, и уравнивание ведется с использованием координатных и азимутальных условий.

Метод отдельных направлений применяют в тех случаях, когда на здании или сооружении невозможно закрепить створ или обеспечить устойчивость концевых опорных знаков створа, и если количество наблюдаемых точек невелико (3-5 точек). Этот метод не такой точный, как метод триангуляции, но он менее трудоёмок. Оба метода позволяют определять смещения точек по осям X и У с высокой достоверностью, но по сравнению с методом створов они отличаются большим объемом измерений и их обработкой.

Согласно ГОСТ 24846-81 для измерения горизонтальных перемещений методом отдельных направлений необходимо установить не менее трех опорных знаков, образующих треугольник с углами не менее 30°.

Величина горизонтального перемещения q (мм), дефор­мационной марки с каждого опорного знака определяется по рас­стоянию L (мм) от опорного знака до марки (измеряемого с по­грешностью 1/2000) и изменению направления между ориентирным знаком и маркой в двух циклах измерений по фор­муле , где r =206265″.

Расстояние от опорного пункта до наблюдаемых точек должно быть не более 1 км. Для контроля устойчивости опорных знаков используют опорные пункты.

Величину и направление горизонтального перемещения каждой марки допускается определять графически.

В случае несовпадения направления вектора горизонтального перемещения с направлением силы, действующей на фундамент здания (сооружения), величину горизонтального перемещения деформационной марки по направлению силы получают как про­екцию вектора на направление силы.

При измерении сдвигов способом отдельных направлений должны применяться высокоточные теодолиты типа Т1, Т2 (используют способ обратной засечки или способ триангуляции). При этом необходимое число круговых приемов и соответствующие погрешности измерений не должны превышать значений, приведенных в табл. 8.3.

Теодолит	Необходи-мое число круго­вых приемов	Допускаемые погрешности намерений, угл. с
Замыкание горизонта	Колебание направлений в отдельных приемах	Колебание 2С в приеме	Средняя квадратическая погреш­ность направле­ния
Т-05 Т-1	0,5 1,0

Этот метод менее трудоемок по сравнению с методом триангуляции, но уступает ему по точности.

Комбинированные методы сочетают в себе линейно-угловые, створные и другие методы наблюдений за горизонтальными смещениями.

Если концевые точки створа включают в триангуляционную сеть, то применяют комбинированный метод наблюдения за сме­щениями (рис.8.10,г). Этот метод совмещает в себе надежность метода триангуляции и простоту створного метода. Каждый цикл створных наблюдений сопровождается определением координат концевых точек вспомогательного створа I-II и измерением отклонения С₁, С₂ и С₃ от него наблюдаемых точек 1, 2 и 3.

Если смещения концевых точек створа по оси X не превышают погрешностей определения координат в триангуляции, то смещения наблюдаемых точек находят створным методом. В противном случае в результаты измерения отклонений наблюдаемых точек от створа вводят поправки.

При комбинированном методе наблюдений в сравнении с мето­дом триангуляции уменьшается объём измерений, в сравнении со створным методом – выше достоверность результатов измерений за счет определения возможных смещений концевых точек вспомога­тельного створа.

Традиционные методы контроля смещения, например плотины, очень трудоёмки. Использование же лазерной автоматической сис­темы (ЛАС) позволяет автоматизировать процесс измерений и обеспечить оперативность получения информации в текущий момент времени.

Сочетание метода триангуляции и створного метода позволяет уменьшить объем измерений по сравнению с методом триангуляции, при этом достоверность результатов комбинированного метода выше, чем у створного за счет определения смещения концевых точек створа, которые включают в сеть триангуляции и определяют их координаты в каждом цикле створных измерений. Этот метод нашел применение при наблюдениях за сдвигами причальных стен набережных.

Также нашли свое применение такие комбинированные методы как сочетание метода триангуляции с прямыми угловыми засечками, сочетание створного метода с методом отдельных направлений.

Способ отвесов. Обычно способ применяют одновременно с полигонометрическими измерениями. В способе прямого отвеса вертикальная линия фиксируется тонкой проволокой, закрепленной на верхнем ярусе сооружения. Снизу подвешивают груз 20 кг.

Положение проволоки в каждом цикле определяется с помощью оптико-электронного или механического переносного координатометра.

Точность определения смещения этим способом составляет 0,5-1 мм. Основным источником погрешностей в способе отвесов является колебание струны.

На гидротехнических сооружениях применяют способ обратного отвеса, в основе которого лежит закон Архимеда. Отвес крепится в основании сооружения. Сверху отвес жестко связан с полым поплавком, плавающим в сосуде с жидкостью. Силой выталкивания нить натягивается в отвесном направлении.

При появлении в основании каких-либо изменений (горизонтальных смещений) соответственно изменяется положение верхней плавающей точки. Величина верхнего перемещения измеряется относительно осей координатного столика при помощи микроскопа.

Для определения абсолютной величины перемещений из тригонометрических наблюдений необходимо знать изменение положения координатного столика от цикла к циклу.

Стереофотограмметрический метод, основанный на применении результатов обработки снимков фототеодолитной съемки, позволяет получать смещения по трем осям координат. Наличие фотографических изображений исследуемого объекта обеспечивает получение смещений любой изобразившейся точки сооружения со сколь угодно большим разрывом во времени производства съемки и обработки снимков. Потенциальные возможности этого метода велики, но они не реализуются полностью по причине малой длины фокусного расстояния выпускаемых фототеодолитов, что не обеспечивает достаточной точности определения смещений. Поэтому он применим только при исследовании со­оружений небольших размеров.

Метод фотограмметрической съемки позволяет одновременно и, что важно, одним прибором измерять смещения неограниченного количества наблюдаемых точек здания или сооружения по двум направлениям координатных осей: по вертикали Z и слагающей горизонтального смещения Х, а стереофотограмметрический метод – по трем направлениям: X, Y и Z.

Определение деформаций зданий и сооружений фотограмметрическим методом выполняют с помощью фототеодолита и стереофотограмметрических приборов. При строгом соблюдении всех требований, предъявляемых к производству фототеодолитной съемки, деформации зданий и сооружений определяют с точностью до 1-3 мм при удалении базиса фотографирования от наблюдаемых точек на 10-20 м.

Способ струны следует применять при прямолинейности
здания или сооружения для непосредственного получения относи­
тельной величины линейного смещения фундаментов, определяе­-
мого как разность отклонения деформационной марки от линии
створа в двух циклах измерений.

Заметим, прежде всего, что при наблюдениях за деформа­циями центральным вопросом является вопрос надежности их определения. Поэтому количественная характеристика деформаций и надежность их определения яв­ляются основными задачами, решаемыми при обработке по­вторных наблюдений любой геодезической деформационной сети.

Заметим также, что в зависимости от характера объекта наблюдений меняется, на первый взгляд, и качественное со­стояние наблюдаемой линейно-угловой сети. Например, если речь идет о наблюдениях за деформациями бортов крупных открытых карьеров добычи полезных ископаемых, подрабаты­ваемых территорий, оползней, геодинамических полигонов, то здесь деформации подвергаются сами пункты линейно-угловой сети, т. е. сама наблюдаемая геодезическая сеть является де­формационной. Такая сеть создается, как правило, в одну ста­дию. Если же наблюдаются деформации промышленного здания, моста и подобных объектов, то геодезическая сеть явля­ется в этом случае основой для наблюдений за деформацион­ными знаками, установленными на объекте, т. е. здесь сущест­вует двухстадийное (двухступенчатое) построение геодезиче­ской сети, с иной организацией работ и иным объемом сбора измерительной информации в разных циклах наблюдений. Од­нако в обоих случаях проблема чистоты обработки результа­тов измерений не снимается, так как и на первых, и на вторых объектах возникает задача определения стабильных и мобиль­ных пунктов сети лишь по результатам повторных измерений ее элементов, т. е. только по «внутренней» информации. В двух­ступенчатых построениях возникает также проблема учета погрешностей исходных данных на точность определения смещений деформационных марок объекта.

Поскольку составляющими вектора деформаций являются изменения координат наблюдаемых точек, очевидно, что урав­нивание сети целесообразно выполнять параметрическим ме­тодом. Известно также, что при сохранении схемы и программы наблюдений в каждом цикле неизменными ослабевает дей­ствие систематических ошибок в значениях самих деформаций.

Чаще всего сети создаются в условной системе координат как нуль-свободные, т. е. с одним исходным стабильным пунк­том, который и принимают за начало условной системы коор­динат. В качестве исходного направления принимают направ­ление на другой пункт сети, обычно смежный с исходным и связанный с ним измерением.

Исходный пункт стремятся выбрать либо в центре сети, ли­бо в ее левом нижнем углу, придав ему такие значения коор­динат, при которых координаты всех пунктов сети были бы по­ложительны. Дирекционный угол исходного направления назна­чают, как правило, равным 0 или 90°.

В основе такого выбора исходных данных лежит чисто гео­метрический подход и соображения удобства вычислений. Вме­сте с тем очевидно, что в качестве ориентирного пункта следу­ет принимать пункт как можно дальше удаленный от исходно­го (начального). Действительно, действие ошибок исходных данных на точность определения положения пунктов сети ана­логично действию ошибок центрирования и редукций.

studopedia.org — Студопедия.Орг — 2014-2021 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.005 с) .

Источник