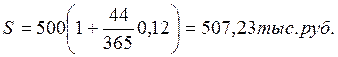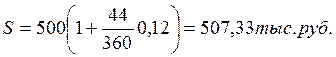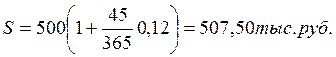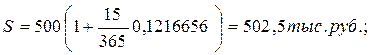Три метода начисления процентов в зависимости от выбранного периода
При использовании простых процентов, когда срок финансовой сделки не равен целому числу лет, периоды начисления процентов выражают дробным числом как отношение числа дней функционирования сделки к числу дней в году:
где t — число дней функционирования сделки (число дней, на которое предоставили кредит);
К— временная база (число дней в году).
В этом случае формула (1.4) примет вид:
(1.5)
В ряде стран для удобства вычислений год делится на 12 месяцев, по 30 дней в каждом, т.е. продолжительность года (К) принимается равной 360 дням. Это так называемая германская практика. Проценты, рассчитанные с временной базой К= 360 дней и приближенным числом дней в месяце (30 дней), называются обыкновенными, или коммерческими.
Существует «французская практика», когда продолжительность года принимается равной К= 360 дней, а продолжительность месяцев в днях соответствует календарному исчислению. Такой метод начисления процентов называют также обыкновенными процентами с точным числом дней ссуды.
И наконец, в ряде стран используется «английская практика», учитывающая продолжительность года в K=365 дней, а продолжительность месяцев — в днях, также соответствующих календарному исчислению, как и при использовании «французской практики», т.е. 28, 29, 30 и 31 день.
В этой связи различают три метода процентных расчетов, которые зависят от выбранного периода начисления.
1. Точные проценты с точным числом дней ссуды («английская практика»). При этом методе определяется фактическое число дней (t) между двумя датами (датой получения и погашения кредита), продолжительность года принимается равной К=365 (366) дней. В этом случае применяется обозначение 365/365.
2. Обыкновенные проценты с точным числом дней ссуды («французская практика»); величина t рассчитывается, как и в предыдущем случае. В этом случае применяется обозначение 365/360.
3. Обыкновенные проценты с приближенным числом дней ссуды («германская практика»); величина t определяется количеством месяцев по 30 дней в каждом? начиная с момента выдачи ссуды и до момента се погашения и точным числом дней ссуды в неполном месяце; продолжительность года К= 360 дней. В этом случае применяется обозначение 360/360.
При точном и приближенном методах начисления процентов день выдачи и день погашения ссуды принимаются за 1 день.
Пример 1.4.
Банк выдал кредит 18 января в размере 500,0 тыс. руб. Срок возврата кредита — 3 марта; процентная ставка — 12,0% годовых; год невисокосный. Определить сумму долга, подлежащую возврату. Необходимо рассчитаем се тремя методами.
Точное число дней ссуды определим по табл. 1 (Приложение 1): 62–18=44 дня.
Такой же результат мы получим, рассчитывая число дней по календарю;
С 18.01 по 31.01 включительно— 14дней;
февраль — 28 дней;
t=45-1=44 дня.
Приближенное число дней ссуды (продолжительность каждого месяца принимается за 30 дней):
январь — 13 дней;
февраль— 30 дней;
t=46-1=45 дней.
Возможные варианты расчета наращенной суммы:
1) по точным процентам с точным числом дней ссуды:
2) по обыкновенным процентам с точным числом дней ссуды:
3) по обыкновенным процентам с приближенным числом дней ссуды:
Приведенный пример свидетельствует, что для кредиторов наиболее предпочтительным является третий вариант начисления процентов.
Между величинами процентного дохода, рассчитанными с использованием различной временной базы (I360 и I365) при равном числе дней ссуды (t) существуют следующие соотношения:
И 
. (1.6)
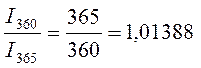
Данные соотношения характеризуют зависимость величины процентного дохода от выбранной временной базы.
По данным примера 1.4(2).
I360=507,33-500=7,33тыс.руб I365=507,23-500=7,23тыс.руб
 |  |
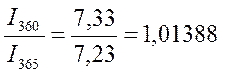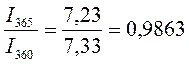Эти соотношения также могут быть использованы при определении эквивалентных процентных ставок, т.е. ставок, приносящих одинаковые процентные доходы при различных временных базах, но равных первоначальных капиталах: ;
Пример 1.5.
При выдаче ссуды 500,0 тыс. руб. на 15 дней по ставке 12% годовых, при К=360 дней, наращённая сумма и процентный доход соответственно составят:
Определить величину процентной ставки, обеспечивающей такой же процентный доход при временной базе К = 365 дней:
i365=1,01388*0,12=0,1216656
Проверим это вычисление:
Как указывалось ранее, при заключении кредитного соглашения может быть установлена постоянная на весь период процентная ставка или изменяющаяся (переменная) процентная ставка. При установлении переменной процентной ставки, т.е. дискретно изменяющейся во времени ставки, наращенная сумма определяется по формуле
(1.8)
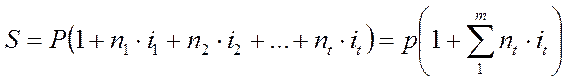
Где it — ставка простых процентов в периоде t;
nt — продолжительность начисления ставки it ;
m — число периодов начисления процентов.
Пример 1.6.
Банк предлагает вкладчикам следующие условия по срочному годовому депозиту: в первое полугодие процентная ставка 12,0% годовых, каждый следующий квартал ставка возрастает на 0,5%, Проценты начисляются только на первоначально внесенную сумму вклада.
Определить наращённую за год сумму, если вкладчик поместил в банк на этих условиях 400,0 тыс. руб.:
Решение:
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Источник
Способ точные проценты с точным числом дней ссуды это
Наращение и дисконтирование по простым процентным ставкам.
2.3 Практика наращеня простых процентов
Поскольку процентная ставка как правило, устанавливается в расчете за год, то при сроке ссуды мене года необходимо определить, какая часть годового процента уплачивается кредитору. Аналогичная проблема возникает и в случаях, когда срок ссуды меньше периода начисления.
Рассмотрим наиболее распространенный в практике случай – с годовыми периодами начисления. Очевидно, что срок ссуды необязательно равен целому числу лет. Выразим срок n в виде дроби
(2.3)
где t — число дней ссуды, K – число дней в году, или временная база начисления процентов ( time basis ).
В этом случае формула 2.3 примет вид
(2.4)
При расчете процентов применяют две временные базы: 
дней (1 месяцев по 30 дней) или 
дней. Если , то получают обыкновенные или коммерческие проценты ( ordinary interest ) , а при использовании действительной продолжительности года (365,366 дней) рассчитывают точные проценты ( exact interest ).
Существует несколько вариантов расчета процентов различным выбором временной базы и способом измерения срока сделки:“Германская практика” – год делиться на 12 месяцев по 30 дней в каждом ( ). Проценты, рассчитываемые с временной базой в 360 дней называют обыкновенными или коммерческими.
“Французская практика” Продолжительность года – 360 дней, а продолжительность месяца в днях соответствует календарю.
“Английская практика” Продолжительность года – 365 дней, а продолжительность месяца в днях соответствует календарю.
Расчет числа дней сделки может быть точным или приближенным. В первом случае вычисляется фактическое число дней между двумя датами. Во втором случае продолжительность сделки определяется числом с месяцев и дней ссуды, при этом продолжительность всех месяцев полагается равным 30 дням. В обоих случаях дата выдачи и дата погашения считается за 1 день.
Возможны применения на практике три варианта расчета простых процентов.
1. Точные проценты с точным числом дней ссуды. Этот вариант, естественно, дает самые точные результаты. Данный способ применяется центральными банками многих стран и крупными коммерческими банками, например, в Великобритании, США. В коммерческих документах он обозначается как 365/365 или АСТ/АСТ.
2. Обыкновенные проценты с точным числом дней ссуды. Этот метод, иногда называемый банковским ( Bankers Rule ), распространен в межстрановых ссудных операциях коммерческих банков, во внутристрановых — во Франции, Бельгии, Швейцарии. Он обозначается, как 365/360 или АСТ/360. Этот вариант дает несколько больший результат, чем применение точных процентов. Заметим. Что при числе дней ссуды, превышающим 360,данный способ приводит к тому, что сумма начисленных процентов будет больше, чем предусматривается годовой ставкой. Например, если t = 364, то n = 364/360 = 1,01111. Множитель наращения за год при условии, что i = 20%, составит 1,20222.
3 . Обыкновенные проценты с приближенным числом дней ссуды. Такой метод применяется тогда, когда не требуется большой точности. Например при промежуточных расчетах. Он принят в практике коммерческих банков Германии, Швейцарии, Дании. Метод условно обозначается как 360/360.
Очевидно, что вариант расчета с точными процентами и приближенным числом дней ссуды лишен смысла и не применяется.
Поскольку точное число дней ссуды в большинстве случаев, но разумеется, не всегда. Больше приближенного (в чем легко убедиться, определив среднее за год, число дней в месяце, которое равно 30,58), то метод начисления процентов с точным числом дней ссуды обычно дает больший рост, чем с приближенным.
Между величиной процентного дохода рассчитанного с использованием различной временной базы при равной продолжительности ссуды существует следующее соответствие:
Эти соотношения могут быть использованы при определении эквивалентных ставок, т.е. ставок, приносящих одинаковые процентные доходы при различных временных базах и равных первоначальных капиталов.
Если общий срок ссуды захватывает 2 смежных календарных года и есть необходимость в делении суммы процентов между ними, то общая сумма начисленных простых процентов составит сумму процентов за каждый год (срок)
,
— части срока, приходящиеся на разные годы.
Источник
Способ точные проценты с точным числом дней ссуды это
Начисление простых процентов
Начисление простых процентов обычно используется в двух случаях: при заключении краткосрочных контрактов (предоставлении краткосрочных кредитов и т.п.), срок которых не превышает одного года, и когда проценты не присоединяются к сумме долга, а выплачиваются периодически.
Ставка процентов обычно устанавливается в расчете за год, поэтому при продолжительности ссуды менее года необходимо выяснить какая часть процента уплачивается кредитору. Для этого величину п выражают в виде дроби
, (1)
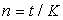
где п — срок ссуды, в долях года,
К — число дней в году (временная база),
t — срок операции (ссуды) в днях.
В этом случае наращенная сумма вычисляется по формуле:
(2)
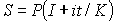
Возможно несколько вариантов расчета процентов, различающихся выбором временной базы К и способом измерения срока пользования ссудой.
Часто за базу измерения времени берут год, условно состоящий из 360 дней (12 месяцев по 30 дней в каждом). В этом случае говорят, что вычисляют обыкновенный или коммерческий процент. В отличие от него точный процент получают, когда за базу берут действительное число дней в году: 365 или 366 (год високосный).
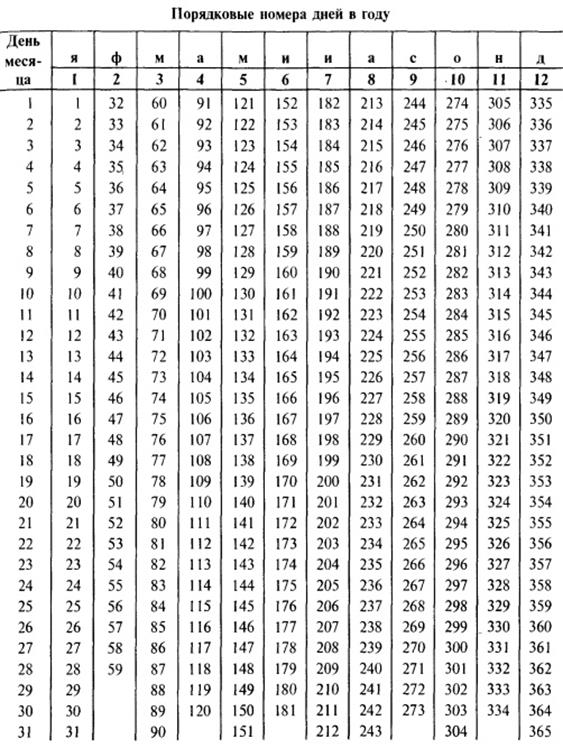
Определение числа дней пользования ссудой также может быть точным или приближенным. В первом случае вычисляют фактическое число дней между двумя датами, во втором — продолжительность ссуды определяется числом месяцев и дней ссуды, приближенно считая все месяцы равными, содержащими по 30 дней. В обоих случаях дата выдачи и дата погашения долга считается за один день. Подсчет точного числа дней между двумя датами можно осуществить, взяв разность этих дат, или с помощью специальной таблицы, в которой представлены порядковые номера дат в году (см. Приложение).
Различные варианты временной базы и методов подсчета дней ссуды, приводят к следующим схемам расчета процентов, применяемых на практике:
— точные проценты с точным числом дней ссуды (британская схема 365/365, когда в году считается 365 дней, полугодие приравнивается к 182 дням и точная длительность месяцев). Используется в Великобритании, США, Португалии;
— обыкновенные проценты с точным числом дней ссуды (французская схема 365/360, в году принимается 360 дней и точная длительность месяцев). Используется во Франции, Бельгии, Испании;
— обыкновенные проценты с приближенным числом дней ссуды (германская схема 360/360, в году считается 360 дней и 30 дней в каждом месяце). Используется в Германии, России, США.
Поскольку точное число дней ссуды в большинстве случаев больше приближенного, то проценты с точным числом дней обычно больше, чем с приближенным.
Вариант расчета с точными процентами и приближенным измерением времени ссуды не применяется.
Точное и приближенное число дней для обыкновенных процентов связаны следующими зависимостями:
i 360 = 0,986301 × i365; i365 = 1,013889 × i360.
Пример 1.
Найти точное и приближенное число дней между 5 марта и 28 сентября.
По таблице (Приложение) 28 сентября является 271 днем, а 5 марта – 64 днем года. Поэтому точное число дней составляет
271 дн. – 64 дн. = 207 дн.
Найдем приближенное число дней между 5 марта и 28 сентября.
5 мес. × 30 дн. + (30 дн. – 5 дн.) + 28 дн. = 203 дн.
Между 5 марта и 28 сентября точное число дней составляет 207, приближенное – 203.
Ссуда в размере 3000 р. положена в банк под 10% годовых с 3 апреля по 29 ноября следующего года (год не високосный). Определить тремя способами наращенную сумму. Какой вариант наращения выгоден банку, а какой вкладчику.
Наращенную сумму найдем по формуле (1.5.).Рассмотрим различные варианты расчета:
1.Точные проценты с точным числом дней ссуды.
Точное количество дней – 604, временная база – 365 дней, тогда
S 1 = 3000 (1 + 0,1 × 604 / 365) = 3496,4 р.
2. Обыкновенные проценты с точным числом дней ссуды.
Точное количество дней – 604, временная база – 360 дней
S 2 = 3000 (1 + 0,1 × 604 / 360) = 3503,3 р.
3. Обыкновенные проценты с приближенным числом дней ссуды
S3 = 3000 (1 + 0,1 × 595 / 360) = 3495,8 р .
Банку выгоден третий вариант расчета наращения. Заемщику – второй вариант расчета наращения.
Источник
