Способ точки встречи прямой с плоскостью

Пересечение прямой с плоскостью

Задача на пересечение прямой с плоскостью — это одна из основных задач, с ее применением сталкиваются при рассмотрении сечения тел плоскостями и пересечения поверхностей.

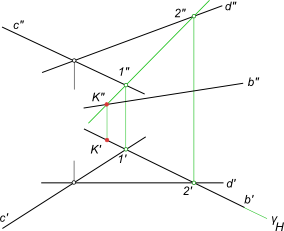
Нахождение точки встречи прямой с плоскостью, заданной пересекающимися прямыми

Плоскость и пересекающая ее прямая занимают общее положение.

(γ ∩ α) = l — прямая, пересекающаяся с прямой b.

На пересечение прямой с плоскостью составляем алгоритм нахождения их точки встречи :

1) проводим через b` горизонтальный след γ_H — горизонтально-проецирующей плоскости γ;

2) определяем фронтальную проекцию линии пересечения l, вспомогательной секущей плоскости γ с данной плоскостью α, используя для этого точки 1` и 2` (принадлежащие данной прямой), в которых горизонтальный след γ_H пересекает прямые c` и d`;

3) определяем точку K»=l»∩b». Зная K», находим K` на пересечении b` с линией проекционной связи.

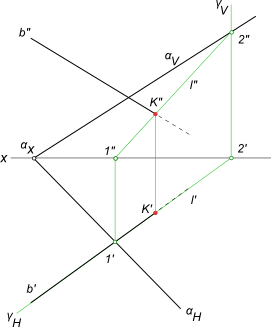
Нахождение точки встречи прямой с плоскостью, заданной параллельными прямыми

Задача по нахождению точки встречи прямой с плоскостью заданной следами.

Алгоритм решения не меняется, если плоскость будет задана параллельными прямыми или прямыми, по которым она пересекает плоскости проекций (следы плоскости).

При решении задач на пересечение прямой с плоскостью в качестве вспомогательных плоскостей применяют проецирующие плоскости. Но в случае, например, профильной прямой они бесполезны и тогда надо применить плоскость общего положения.

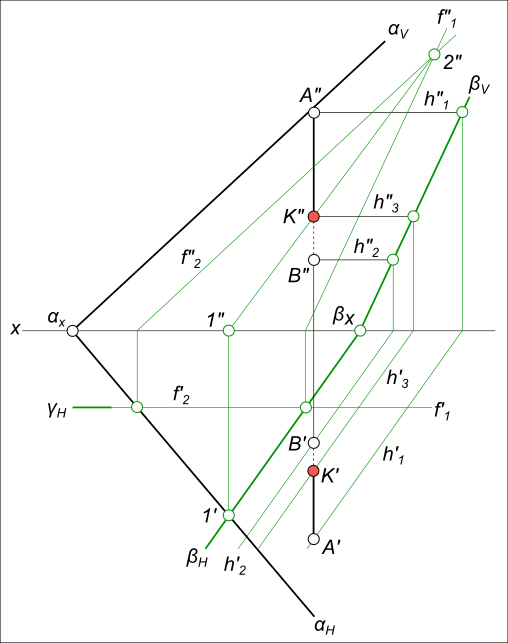
Найти точку встречи профильной прямой AB с плоскостью α заданной следами

Алгоритм выполнения геометрических построений: 1) Заключаем отрезок AB во вспомогательную секущую плоскость общего положения β; 2) Определяем проекции линии пересечения 1-2, вспомогательной секущей плоскости β с данной плоскостью α; 3) Определяем проекцию K» точки K на пересечении 1″-2″ с прямой A»B». Проекция K` точки K может быть найдена: — на пересечении A`B` с 1`-2`; — или как принадлежащая плоскостям α и β.

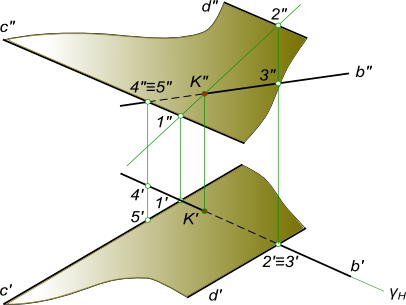
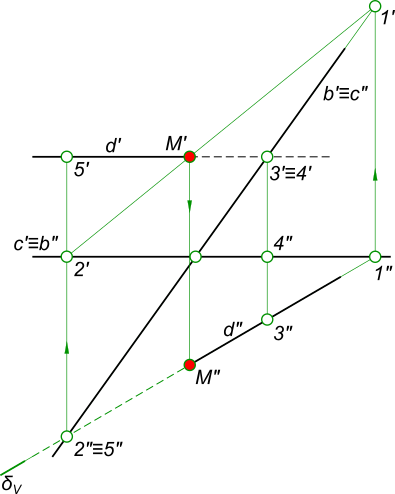
Найти точку встречи прямой d с плоскостью α(b, c), определить видимость

Алгоритм выполнения геометрических построений: 1) Заключаем прямую d во вспомогательную секущую фронтально проецирующую плоскость δ; 2) Определяем проекции линии пересечения 1-2, вспомогательной секущей плоскости δ с данной плоскостью α; 3) Определяем проекцию K` точки K на пересечении 1`-2` с прямой d`. Проекцию K» точки K находим в пересечении d» с линией проекционной связи.

Данный способ решения задачи — найти точку встречи профильной прямой с плоскостью заданной следами применен в статье: Сечение пирамиды плоскостью

Определение видимости пересечения прямой с плоскостью на плоскостях проекций выполняем, используя Конкурирующие точки 2, 3 и 4, 5.

Источник

Способ точки встречи прямой с плоскостью

Контрольные задания по теме:
Рабочая тетрадь задача 39, задача 40а, задача 40б

Точка принадлежит прямой, если её проекции лежат на одноимённых проекциях этой прямой (рис. 21а).

Точка принадлежит плоскости, если она лежит на прямой, лежащей в этой плоскости (рис.21б).

Прямая принадлежит плоскости, если она проходит через две точки, лежащие в этой плоскости (рис.21в).

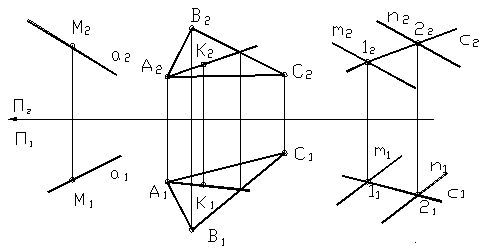
Рисунок 21

Прямая параллельна плоскости, если она параллельна любой прямой, лежащей в этой плоскости. На рисунке 22 изображена прямая t, параллельная прямой b, принадлежащей плоскости Σ: t // b Î Σ (a Ç b).

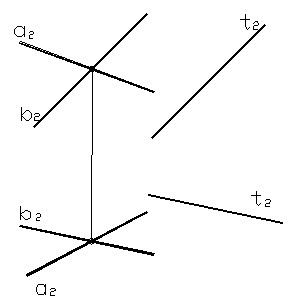
Рисунок 22

Через любую точку пространства можно провести бесконечное множество прямых, параллельных данной плоскости.

Это задача на определение общей точки прямой и плоскости. Её называют также точкой встречи. Рассмотрим пересечение прямой с плоскостью частного положения.

Плоскость Σ задана треугольником АВС и является горизонтально проецирующей плоскостью. Точка встречи прямой k с плоскостью Σ определяется по горизонтальной проекции. Фронтальная проекция точки К достраивается с помощью линии связи. Символическая запись будет выглядеть следующим образом: k Ç Σ (ABC) = K.

Видимость прямой относительно плоскости определяется при помощи фронтально-конкурирующих точек 1 и 2.

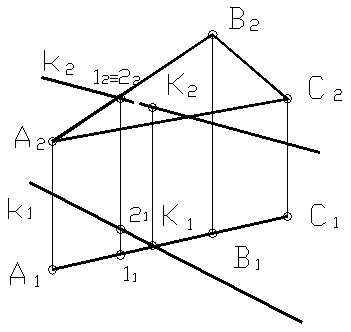
Рисунок 23

Пересечение прямой с плоскостью общего положения изображено на рисунке 24. В этом случае нужно заключить прямую в проецирующую плоскость.

t Î Σ ^ П 2 – прямая t принадлежит плоскости Σ, которая перпендикулярна горизонтальной плоскости проекций. Линия пересечения этой плоскости с данной — линия (1, 2). Затем находится точка пересечения этой линии с прямой t , которая и будет являться точкой встречи прямой и плоскости. Видимость прямой относительно плоскости определяется при помощи конкурирующих точек. Возьмем горизонтально конкурирующие точки 3 и 4. Так как точка 3, принадлежащая прямой, оказалась ниже чем точка 4, следовательно, прямая на горизонтальной плоскости справа от точки пересечения невидима. Затем берем фронтально конкурирующие точки 1 и 5. Точка 1, принадлежащая плоскости, лежит ближе, следовательно, прямая находится за плоскостью, и она на фронтальной проекции невидима от точки 1 до точки К.

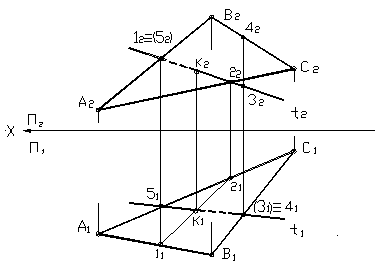
Рисунок 24

К особым прямым, принадлежащим плоскости, относятся горизонталь, фронталь и профильная прямая. Построение этих прямых используется при решении многих задач по начертательной геометрии. Их изображение дано на рисунке 25. Причём на горизонтальной плоскости горизонталь имеет натуральную величину, на фронтальной плоскости — фронталь и на профильной плоскости – профильная прямая.

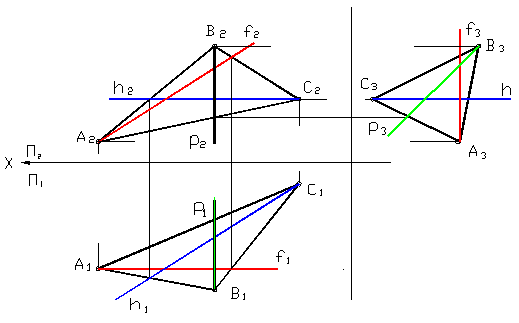
Рисунок 25

1. Сформулируйте условия принадлежности точки плоскости и прямой плоскости.

2. Как построить прямую параллельную заданной плоскости?

3. Вспомните этапы решения задачи на определение точки пересечения прямой и плоскости.

4. Какие точки называются конкурирующими?

5. Как провести в плоскости горизонталь и фронталь?

6. Какие еще особые прямые плоскости вы знаете?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Построение точки пересечения прямой и плоскости

Известно, что прямая пересекает плоскость, если она не принадлежит этой плоскости и не параллельна ей. Следуя приведенному ниже алгоритму, найдем точку пересечения прямой a с плоскостью общего положения α, заданной следами h_0α, f_0α.

1. Через прямую a проводим вспомогательную фронтально-проецирующую плоскость γ. На рисунке обозначены её следы h_0γ, f_0γ.
2. Строим проекции прямой AB, по которой пересекаются плоскости α и γ. В данной задаче точка B’ = h_0α ∩ h_0γ, A» = f_0α ∩ f_0γ. Точки A’ и B» лежат на оси x, их положение определяется по линиям связи.
3. Прямые a и AB пересекаются в искомой точке K. Её горизонтальная проекция K’ = a’ ∩ A’B’. Фронтальная проекция K» лежит на прямой a».

Алгоритм решения останется тем же, если пл. α будет задана параллельными, скрещивающимися прямыми, отсеком фигуры или другими возможными способами.

Видимость прямой a относительно плоскости α. Метод конкурирующих точек

1. Отметим на чертеже фронтально-конкурирующие точки A и С (рис. ниже). Будем считать, что точка A принадлежит пл. α, а С лежит на прямой a. Фронтальные проекции A» и С» совпадают, но при этом т. A и С удалены от плоскости проекций П₂ на разное расстояние.
2. Найдем горизонтальные проекции A’ и C’. Как видно на рисунке, точка C’ удалена от плоскости П₂ на большее расстояние, чем т. A’, принадлежащая пл. α. Следовательно, участок прямой а», расположенный левее точки K», будет видимым. Участок a» правее K» является невидимым. Отмечаем его штриховой линией.
3. Отметим на чертеже горизонтально-конкурирующие точки D и E. Будем считать, что точка D принадлежит пл. α, а E лежит на прямой a. Горизонтальные проекции D’ и E’ совпадают, но при этом т. D и E удалены от плоскости П₁ на разное расстояние.
4. Определим положение фронтальных проекций D» и E». Как видно на рисунке, точка D», находящаяся в пл. α, удалена от плоскости П₁ на большее расстояние, чем т. E», принадлежащая прямой a. Следовательно, участок а’, расположенный правее точки K’, будет невидимым. Отмечаем его штриховой линией. Участок a’ левее K’ является видимым.

Источник

Определение точки встречи прямой с плоскостью

Определение точки встречи прямой общего положения с плоскостью общего положения.

Рис. 67

Эта позиционная задача (как и большинство других позиционных задач) решается с помощью вспомогательной плоскости. Пусть задана прямая n общего положения и плоскость α общего положения. Необходимо найти их точку пересечения К (рис. 67). Задача решается в следующей последовательности.

1. Заданная прямая n заключается во вспомогательную плоскость β: nÌβ.

2. Строится прямая l пересечения заданной плоскости α со вспомогательной плоскостью β: l(12)= α∩β.

3. Построенная прямая 12 и заданная прямая n лежат в одной плоскости β, а значит будут пересекаться между собой: K=l∩n. Их общая точка K является общей для прямой n и плоскостей и β, а значит, является искомой точкой пересечения прямой n и плоскостиα.

В качестве вспомогательной плоскости чаще всего используют проецирующие плоскости.

Рассмотрим пример решения задачи на комплексном чертеже (рис. 68).

Рис. 68

Заключаем прямую n во вспомогательную горизонтально проецирующую плоскость β, которую зададим горизонтальным следом β₁ (горизонтальная проекция плоскости). Причем след β₁ должен совпадать с горизонтальной проекцией прямой n₁. Далее находим прямую l пересечения вспомогательной плоскости β с заданной плоскостью α. Сторона АВ пересекается с плоскостью β в точке 1, а сторона АС – в точке 2. Сначала отмечаем горизонтальные проекции точек 1₁ и 2₁, а затем с помощью вертикальных линий связи находим фронтальные проекции точек 1₂ и 2₂ соответственно на фронтальных проекциях сторон треугольника А₂В₂ и А₂С₂. Таким образом, плоскости пересекаются по прямой l(12). Теперь можно определить фронтальную проекцию К₂ искомой точки. Она будет являться точкой пересечения фронтальных проекций построенной прямой l(1₂2₂) и заданной прямой n₂. Горизонтальная проекция К₁ определяется с помощью вертикальной линии связи на горизонтальной проекции прямой n₁.

Затем нужно определить видимость прямой n относительно плоскости α. Для определения видимости на необходимо воспользоваться горизонтально конкурирующими точками 2 и 3 (точка 2 лежит на стороне АС треугольника, а точка 3 – на прямой n). Видимость прямой на π₂ определяем с помощью фронтально конкурирующих точек 4 и 5 (точка 5 лежит на стороне ВС, а точка 4 – на прямой n). Направление взгляда при определении видимости проекций конкурирующих точек на эпюре показана символом (⇩).

Определение точки встречи прямой общего положения с проецирующей плоскостью.

Постановка задачи. Пусть задана горизонтально-проецирующая плоскость α треугольником ∆АВС и прямая n общего положения (рис. 69). Необходимо определить точку встречи К прямой n с плоскость α: К =n∩α.

Решение. Проекция точки встречи К₁ прямой n с плоскостью α однозначно определяется как точка пересечения горизонтальной проекции плоскости (вырожденной в прямую) с одноименной проекцией прямой: К₁=l₁∩α₁(∆A₁B₁C₁).

Рис. 69

Недостающая фронтальная проекция точки встречи К₂ находится по принадлежности точка К прямой n: КÌn => К₁Ìn₁.

Видимость прямой n относительно плоскости α определяется только для фронтальной плоскости проекций, т.к. на π₁ обе проекции видны. Видимость определяется с помощью фронтально конкурирующих точек 1 и 2 (точка 2 лежит на стороне ВС треугольника, а точка 1 – на прямой n). Направление взгляда при определении видимости проекций конкурирующих точек на эпюре показана символом (⇧).

В задачах, где используется фронтально-проецирующая пло­скость, при определении точки встречи последовательность решения аналогична выше указанному, только в них известной является фронтальная проекция искомой точки.

Определение точки встречи проецирующей прямой с плоскостью общего положения.

Постановка задачи. Пусть задана горизонтально-проецирующая прямая n (рис. 70) и плоскость общего положения α(∆АВС). Необходимо определить точку встречи К прямой n с плоскость α: К =n∩α.

Решение. Очевидно проекция точки встречи К₁ прямой с плоскостью α совпадает с вырожденной проекцией прямой n₁: К₁ ≡n₁: Учитывая то, что точка К принадлежит плоскости α, то задача сводится к определению недостающей проекции точки принадлежащей плоскости. Для этого, вначале, через вырожденную проекцию n₁ проводится проекция вспомогательной прямой l₁ в предположении, что эта прямая l принадлежит плоскости α: lÌα => l₁Ìα₁. Затем, достраивается недостающая фронтальная проекция этой прямой l₂. Точка пересечения фронтальных проекций заданной n₂ и вспомогательной l₂ прямых является искомой проекцией точки встречи К₂.

Видимость прямой n относительно плоскости αопределяется только для фронтальной плоскости проекций, т.к. на π₁ обе проекции видны. Видимость определяется с помощью фронтально конкурирующих точек 2 и 3 (точка 2 лежит на стороне АС треугольника, а точка 3 – на прямой n). Направление взгля­да при определении видимости про­екций конкурирующих точек на эпюре показана символом (⇧).

Рис. 70

В задачах, где используется фронтально-проецирующая прямые, при определении точки встречи последовательность решения аналогична выше указанному, только в них известной является фронтальная проекция искомой точки.

7.4. Контрольные вопросы

1. Какие прямые относятся к главным линиям плоскости?

2. Какая прямая называется горизонталью плоскости и как она строится на эпюре?

3. Какая прямая называется фронталью плоскости и как она строится на эпюре?

4. Какая прямая называется линией наибольшего ската плоскости и как она строится на эпюре?

5. Какая прямая называется линией наибольшего наклона плоскости и как она строится на эпюре?

6. Как строится линия пересечения плоскости общего положения проецирующей плоскостью?

7. Можно ли провести проецирующую плоскость через прямую общего положения?

8. Как определяются точки встречи прямой общего положения с плоскостью общего положения?

9. Как определяется видимость на эпюре прямой относительно плоскости?

10. Как определяются точки встречи проецирующей прямой с плоскостью общего положения?

11. Как определяются точки встречи прямой общего положения с плоскостью частного положения?

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Источник