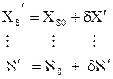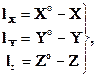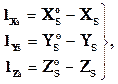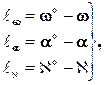Уравнивание связок проектирующих лучей
Математическая модель построения блока на основе уравнивания связок проектирующих лучей является дальнейшим развитием изложенного ранее (§ 87.4) способа построения маршрутной сети на основе уравнивания связок, и заключается в использовании зависимости между координатами точек снимков и местности (3.16, 13.13).
Технологическая последовательность построения и уравнивания блока включает измерение координат и параллаксов точек стереопар, исправление их за влияние систематических деформаций, выбор начальных значений неизвестных (координат определяемых точек и элементов внешнего ориентирования снимков), составление для каждой точки двух уравнений поправок вида (13.15), а для точек с известными координатами -уравнений (13.16), решение методом последова-
тельных приближений под условием [vvp] = min. В результате получают уравненные координаты определяемых точек и элементы внешнего ориентирования всех снимков блока.
При реализации этого решения возникают две проблемы, одна из которых связана с применением метода итераций, а вторая — с совместным решением больших систем нормальных уравнений.
Применение итеративного уравнивания, особенно больших по объему систем, порождает проблему его сходимости, зависящую, в том числе, и от близости начальных значений неизвестных к уравненным, поскольку их существенные различия могут привести к тому, что погрешности отыскания неизвестных окажутся сопоставимыми с самими неизвестными. Кроме того, итеративное уравнивание создает определенные трудности отыскания и локализации ошибочных данных. По этой причине уравниванию связок проектирующих лучей всегда предшествуют фотограмметрические построения иными способами, например, полузависимых моделей с последующим объединением маршрутов в блок. Это позволяет не только получить достаточно близкие к окончательным значения неизвестных, но и проконтролировать результаты измерений путем проверки выполнения тех или иных условий. Так, при взаимном ориентировании проверяется условие равенства нулю остаточных поперечных параллаксов точек стереопары; при объединении смежных моделей — условие равенства длин проектирующих лучей; при объединении маршрутов или моделей в блок — равенство координат связующих точек; при внешнем ориентировании — остаточные расхождения координат опор-ныхОбчекм совместно уравниваемой сети в современных условиях не является определяющим, хотя и создает определенные неудобства. Так, построение и уравнивание среднего по размерам блока, включающего 250 снимков и 2000 определяемых точек (по три в каждой стандартной зоне), требует совместного решения 7,5 тыс. уравнений, избежать которое можно двумя путями, различающимися способами реализации многогруппового метода уравнивания. В обоих случаях в исходных условиях (13.14) выделяется две группы условно независимых параметров: элементы внешнего ориентирования снимков Х$, Ys, Z$, а, со, х и координаты определяемых точек X, Y, Z.
Метод последовательной вставки неизвестных 1 предполагает минимизацию [ии] для каждой точки и каждого снимка в отдельности, т.е. использование двух условно независимых групп
Машимов ММ. Итеративный метод построения и уравнивания пространственной фототриангуляции на ЭЦВМ с последовательной вставкой неизвестных // Изв. ВУЗов, «Геодезия и аэрофотосъемка», вып. 3, 1966.
Процесс итераций состоит в последовательном отыскании точек экстремума функции (13.14) по группам неизвестных (13.26) с одновременным уточнением их приближенных значений. Сначала все точки принимаются за опорные и по ним уточняются элементы внешнего ориентирования снимков; затем за известные принимаются элементы внешнего ориентирования всех снимков, по которым уточняются координаты определяемых точек. Так выполняется несколько приближений, которые заканчиваются, когда изменения элементов внешнего ориентирования и координат определяемых точек в двух соседних приближениях становятся меньше установленного допуска.
Второй путь реализации многогруппового метода уравнивания, широко используемый в исследованиях и компьютерных программах д.т.н. И.Т. Антипова [2], основан на построении матрицы нормальных уравнений неизвестных, распадающейся на четыре подматрицы:
| А С \с Т в | X | 5S ST | + | LS\ LT |
две из которых (Л, В) являются близдиагональными и связаны с выделенными группами условно независимых неизвестных, а две других (С, С 7 ) являются связующими. Подматрица А представлена клетками размером 6×6 элементов, соответствующими элементам внешнего ориентирования одного снимка, а подматрица В — клетками размером 3×3 элементов, соответствующими одной определяемой точке.
Таким образом, при уравнивании сети, состоящей из п снимков и m определяемых точек при решении системы нормальных уравнений (13.27) оперируют с 6п независимыми подматрицами размером 6×6, Зт подматрицами размером 3×3 и одной подматрицей размером бпхЗт.
Принципы уравнивания с самокалибровкой
ч Практическая эффективность строгих способов построения фототриангуляционных построений, базирующихся на уравнивании независимых моделей и связок проектирующих лучей, определяется остаточными влияниями систематических искажений, вызываемых деформацией фотоматериала, атмосферной рефракцией, дисторсией объектива и т.п. Поэтому уравнивание фотограмметрических построений можно назвать строгим только тогда, когда оно предполагает опреде-
ление и учет систематических искажений. Такое уравнивание в фотограмметрической литературе принято называть уравниванием с самокал ибровкой.
Рассматриваемые систематические искажения изображения учитываются путем исправления либо измеренных координат точек снимков, либо фотограмметрических координат точек построенной сети.
Учет искажений координат точек снимков основывается на использовании следующих зависимостей между исправленными х°, у 0 , измеренными х, у координатами точек снимков и их суммарными систематическими ошибками ах. cjy:
где ox, vy — поправки к непосредственно измеренным величинам.
Суммарные систематические искажения а определяются в процессе строгого уравнивания либо как конкретные поправки, либо через параметры функции самокалибровки, описывающей закономерности изменения систематических погрешностей по полю снимка. Во втором случае они представляются полиномами вида
С учетом этого условия (13.14), на основе которых выполняется уравнивание связок проектирующих лучей, примут вид
Источник
Построение и уравнивание маршрутной и блочной фототриангуляции по методу связок
Определение элементов внешнего ориентирования снимка по опорным точкам (обратная фотограмметрическая засечка)
Опорной точкой будем называть точку, опознанную на местности и на снимке, геодезические координаты которой на местности известны.
Для определения элементов внешнего ориентирования снимка воспользуемся уравнениями коллинеарности (1.3.12), которые представим в виде
; (1.5.1)
;
. (1.5.2)
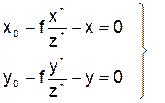
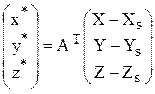
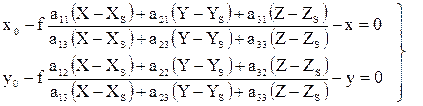
Если на снимке измерены координаты изображений опорных точек, то каждая опорная точка позволяет составить 2 уравнения (1.5.2), в которых известны значения координат х,у изображения опорной точки в системе координат снимка Sxyz, геодезические координаты опорной точки в системе координат объекта OXYZ и элементы внутреннего ориентирования снимка f,x0,y0.
Неизвестными величинами в уравнениях (1.5.2) являются 6 элементов внешнего ориентирования снимка Xs, Ys, Zs, w, a, À.
Следовательно, для определения 6 неизвестных элементов внешнего ориентирования снимка достаточно иметь не менее 3 опорных точек. При этом опорные точки на местности не должны располагаться на одной прямой. Если имеются 3 опорные точки, координаты изображений которых на снимке измерены, можно составить систему из 6 уравнений (1.5.2) с 6 неизвестными. В результате решения этой системы уравнений можно найти значения элементов внешнего ориентирования снимка.
В связи с тем, что уравнения (1.5.2) нелинейные, решение системы уравнений непосредственно достаточно сложно, поэтому систему уравнений (1.5.2) решают методом приближений.
Для этого уравнения (1.5.2) приводят к линейному виду, раскладывая их в ряд Тейлора с сохранением членов только первого порядка малости, и переходят к уравнениям поправок.
. (1.5.3)
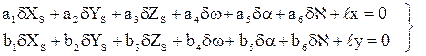
В уравнениях (1.5.3):
dXs, … ,dÀ — поправки к приближенным значениям неизвестных элементов внешнего ориентирования снимка Xs 0 ,…,À 0 ;
ai, bi – частные производные от уравнений (1.5.2) по соответствующим аргументам (например, коэффициент а4 является частной производной от первого уравнения (1.5.2) по аргументу w,то есть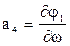
);
ℓх, ℓу – свободные члены.
Значения коэффициентов уравнений (1.5.3) ai, bi вычисляются по известным значениям координат точек снимка и местности х,у и X,Y,Z, известным значениям элементов внутреннего ориентирования снимка f,x0,y0 и приближенным значениям неизвестных Xs 0 ,…,À 0 .
Свободные члены ℓх, ℓу вычисляются по формулам (1.5.2) таким же образом.
В результате решения системы уравнений поправок (1.5.3) находят поправки к приближенным значениям неизвестных и вычисляют уточненные значения неизвестных.
По уточненным значениям неизвестных повторно составляют уравнения поправок (1.5.3) и решают полученную систему уравнений.
Решения повторяют до тех пор, пока величины поправок, найденные в результате решения, не станут пренебрежимо малыми.
В случае если на снимке измерено более трех изображений опорных точек, то для каждой точки составляют уравнения поправок вида:
; (1.5.4)
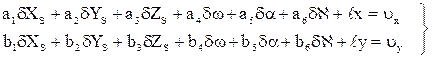
Решение полученной системы уравнений (1.5.4) производят методом приближений, по методу наименьших квадратов (под условием V T V = min).
При построении сети фототриангуляции методом связок для каждого изображения точки (определяемой и опорной), измеренного на снимке составляются уравнения коллинеарности:
(1.6.1)
;
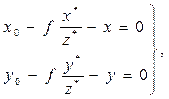
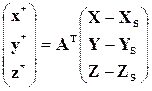
x,y – координаты изображения точки местности, измеренной на снимке;
X,Y,Z – координаты точки местности в системе координат объекта OXYZ;
XS,YS, ZS – координаты центров проекции снимка в системе координат объекта;
А – матрица преобразования координат, элементы a ij которой являются функциями угловых элементов внешнего ориентирования снимка.
 |
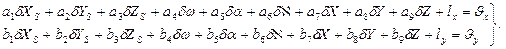Уравнения поправок, соответствующие условным уравнениям (1.5.1) имеют вид: (1.6.4)
Для каждой планово-высотной опорной точки составляются уравнения поправок:
(1.6.5)
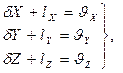
X,Y,Z – измеренные координаты опорной точки,
X o ,Y o ,Z o – приближенные значения координат опорной точки.
Для плановой опорной точки составляются два первых уравнения из системы уравнений (1.6.5), а для высотной опорной точки третье уравнение.
Если с помощью системы GPS были определены координаты центров проекций снимков S, то для каждого центра проекции составляются уравнения поправок:
(1.6.6)
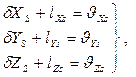
Xs,Ys,Zs – измеренные координаты центров проекции снимков,
X o S, Y o S, Z o S – их приближенные значения.
В случае, если при съемке с помощью навигационного комплекса, включающего инерциальную и GPS системы, были определены угловые элементы внешнего ориентирования снимков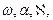 
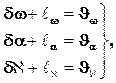
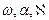
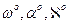
для каждого снимка составляются уравнения поправок:
(1.5.7)
— измеренные значения угловых ЭВО,
— их приближенные значения.
Полученную таким образом систему уравнений поправок решают методом приближений по методу наименьших квадратов под условием V T V=min.
В результате решения находят значения элементов ориентирования всех снимков сети и координаты точек сети в системе координат объекта.
В первом приближении в уравнениях поправок (1.5.5), (1.5.6) и (1.5.7) приближенные значения неизвестных принимаются равными их измеренным значениям.
С геометрической точки зрения сеть фототриангуляции по методу связок строится под условием пересечения соответственных проектирующих лучей связок в точках объекта (рис. 1.6.1):
Общее количество неизвестных, определяемых при построении и уравнивании блочной сети, можно определить по формуле:
(1.6.8)
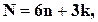
где n – количество снимков в сети;
k – количество определяемых точек (включая опорные геодезические точки).
Общее количество уравнений поправок можно определить по формуле:
, (1.6.9)
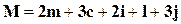
m – общее количество измеренных на снимках точек;
c — количество планово-высотных опорных точек;
i — количество плановых опорных точек;
l – количество высотных опорных точек;
j – количество центров проекций снимков, измеренных с помощью системы GPS.
Рассчитаем величины M и N для блочной сети изображенной на рис. 1.6.2, состоящей из двух маршрутов, в каждом из которых 4 снимка.
 |
 |
 |
| |
 | |
 | |
| | | |
 |
|  |
| |
 |
 |
|
|
 |  |
 | |
 |
| |
| |
Рис. 1.6.2
— 
— главная точка снимка;
— точка сети;
|
— планово-высотная точка;
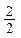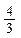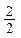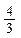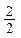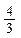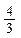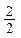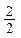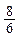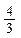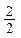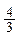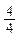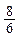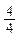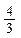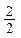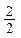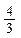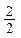— количество точек, измеренных на снимках (в числителе – количество точек, измеренных на стереокомпараторе или аналитической стереофотограмметрической системе, а в знаменателе – количество точек, измеренных на цифровой фотограмметрической системе).
Для блочной сети, изображенной на рис. 1.6.1, n=8, а k=20, поэтому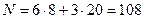 
.
Из рис. 1.6.2 следует, что m=72, если снимки измерялись на стереокомпараторе или аналитическом стереофотограмметрическом приборе, или m=60 в случае, если снимки измерялись на цифровой фотограмметрической системе
, а 
, если снимки измерялись на стереокомпараторе или аналитической стереофотограмметрической системе, и
, если снимки измерялись на цифровой фотограмметрической системе.
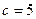
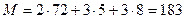
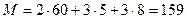
Источник
