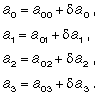5.2.2 Способ свободной станции
Способ рассчитан на выполнение съемки электронным тахеометром, установленным в произвольно выбранной съемочной точке, не привязанной геодезическими измерениями к каким-либо пунктам сети или другим съемочным точкам. Для определения площади способом свободной станции не требуется наличие геодезической сети.
Рис 5.5 Схема измерений на свободной станции
Э 
Направлениями из съемочной точки на пикеты вычисляемая площадь делится на секторы. Площади секторов вычисляют по формуле 
где i – номер сектора; βi = Ni+1 – Ni – острый угол треугольника, вычисляемый как разность направлений на смежные пикеты i и i + 1.
Площадь всего участка найдем, суммируя площади секторов:
Выше уже отмечено, что пикеты 1, 2, . n надо выбирать так часто, чтобы образуемая ломаная линия практически не отличалась от кривой.
Место для съемочной точки А может быть выбрано и вне ограничивающего площадь контура. Необходимость такого выбора может возникнуть, например, при определении площади озера.
Искомая площадь Р (рис. 5.6) в этом случае равна разности площадей
З
Рис. 5.6 Свободная станция вне контура участка
десьР1 – сумма площадей секторов, ограниченных отрезками прямых от съемочной точки А до точек 1, 2, 3, 4, 5, 6, 7, расположенных на дальней границе участка, и Р2 – сумма площадей секторов, ограниченных отрезками прямых от съемочной точки А до точек 7, 8, 9, 10, 11, 1 на ближней границе участка.
Площадь каждого сектора вычисляется по формуле (5.6).
5.2.3 Способы нескольких свободных станций
Если с одной съемочной точки видны не все пикеты, расположенные на границе участка, можно выполнить определение площади, используя несколько свободных станций.
Рис. 5.7 Цепочка свободных станций
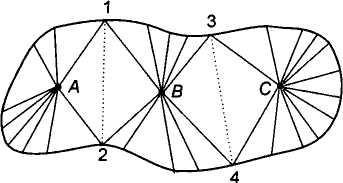
На рис. 5.8 показана схема участка, значительная средняя часть которого недоступна для измерений (залесенность, застройка).
Рис. 5.8 Съемка площади с недоступной частью
Места для установки электронного тахеометра выбраны в точках А, В и С, связанных между собой только общими пикетами 1, 2, 3. Площади, ограниченные границей контура и пунктирными линиями, проведенными через названные пикеты, можно вычислить, измерив показанные на схеме расстояния и горизонтальные направления на точки, аппроксимирующие криволинейную границу участка. При этом площади секторов определятся по формуле (5.6), а вся площадь, окружающая станцию (А, В или С), — по формуле (5.7). Например, площадь РА, окружающая пункт А, будет вычислена как сумма восьми секторов. Аналогично будут вычислены площади РВ и РС.
Для вычисления площади треугольника 123 определим длины его сторон:


Источник
Метод свободной станции

В инженерно-геодезическом обеспечении строительства проблемой является сохранность центров геодезических пунктов, как опорной, так и разбивочных сетей (внешней и внутренних). Удаление центров пунктов от объекта строительства и районов земляных работ затрудняет их использование при обеспечении строительства.
Применение метода свободной станции с применением электронного тахеометра позволяет получить значительный эффект. Особенность этого метода заключается в том, что прибор в процессе измерений устанавливается не над центром исходного или определяемого геодезического пункта, а в некоторой точке, положение которой оптимально для координирования и ориентирования прибора, а также для передачи проектных значений координат и высот на выносимые точки (контрольные точки элементов строительных конструкций, элементов трассы и др.).

Рисунок 1. Схема измерений методом свободной станции: А, Б, В, Г, … – исходные пункты, доступные для измерений с данной станции; а, б, в, г, … – выносимые проектные или координируемые точки; МП – возможное местоположение прибора, предоставляющее видимость на исходные пункты и определяемые точки
Следует отметить, что в режиме свободной станции с помощью электронного тахеометра можно работать в пространственной системе координат (совмещенные плановая и высотная сети – векторная сеть). В зависимости от условий решаемой задачи измерения могут проводиться как с применением отражателя и специальной пленки, так и в безотражательном режиме.
Для однозначного (бесконтрольного) определения планово‑высотного положения геометрического центра прибора и его ориентировки в принятой системе координат достаточно произвести позиционирование на два исходных пункта, планово‑высотные координаты которых известны. Измеряются: две наклонные дальности, один горизонтальный и два вертикальных угла. В современных тахеометрах зарубежных фирм-производителей имеется соответствующее встроенное программное обеспечение, позволяющее работать в различных режимах. На данном этапе следует работать в режиме «координирование прибора».

Например, известны плановые координаты и высоты (отметки) двух пунктов А и Б: Xa, Ya, Ha, Xb, Yb, Hb.
Измерены наклонные дальности Sa, Sb, их горизонтальные направления, по разности которых вычисляют горизонтальный угол Bab, также измерены вертикальные углы βA, βБ.
Вычисляют горизонтальные проложения по известной формуле:
Из решения обратной геодезической задачи вычисляют горизонтальное проложение между центрами исходных пунктов и дирекционные (прямой и обратный) углы:
Значение дирекционного угла определяют по знакам приращений координат, как это принято при решении обратной геодезической задачи.
Из решения треугольника А0 Б0 С по теореме синусов вычисляют его горизонтальные углы при вершинах А и Б:
Наличие одной избыточной величины в треугольнике позволяет провести контроль измерений и вычислений, вычислив невязку в треугольнике:
Ваb +А0 + Б0 –1800 = W
Вычисляют дирекционные углы направлений вдоль измеренных наклонных дальностей:
Вычисляют приращения координат от любой исходной точки до центра прибора по формулам решения прямой геодезической задачи:
Вычисляют координаты центра прибора:
Ориентировкой угломерной шкалы горизонтального круга служат дирекционные углы сторон СА и СБ.
Высотная отметка центра прибора определяется с контролем от двух исходных пунктов по превышениям, получаемым из тригонометрического нивелирования:
В современных электронных тахеометрах все вышеуказанные вычисления ведутся в автоматическом режиме, запоминаются и могут быть использованы в дальнейшей работе. Опыт работы на реальных объектах показывает, что координирование и ориентирование центра прибора указанным методом необходимо производить от трех и более исходных пунктов. В этом случае прибор указывает не только искомые величины, но и ошибки их определения. Более трех исходных пунктов берут в случае, если происходит изменение планово‑высотного положения центров исходных пунктов и необходимо произвести анализ их стабильности.
После того как произведено координирование и ориентирование прибора, приступают в режиме «съемка» к координированию центров разбивочных сетей. При этом в случае необходимости параллельно можно производить вынос в проектное положение элементов строительных конструкций, детальную разбивку элементов трассы и т. п.
С одной свободной станции можно производить координирование и разбивку любого числа видимых точек. В реальных условиях таких свободных станций на объекте может быть любое, достаточное для работы число. Для того чтобы обеспечить необходимую и однородную точность координатных определений, производство уравнительных вычислений и оценку точности результатов измерений, измерения на каждой свободной станции производят с перекрытием, особенно важно выполнение этого условия при создании разбивочных сетей. Особо важные конструктивные элементы должны выноситься с двух станций для контроля и оценки точности результатов.
Вычисление плановых координат и высотных отметок определяемых точек производится по формулам связи параметрического и полярного задания пространственного вектора.
Если необходимо произвести вынос контрольных точек по проектным координатам, то они предварительно заносятся в электронную базу данных прибора. При позиционировании прибор выдает отклонения точки позиционирования от проектного положения по каждой из трех ее координат. По этим данным производится точная доводка до проектного положения.
Достаточно эффективно в координатном режиме выносить центры пересечения строительных осей сооружения.
Опорные геодезические сети на строительных горизонтах создаются для обеспечения необходимых условий по выносу в проектное положение строительных осей и основных элементов строительных конструкций. Для рационального решения этих задач важным моментом является расположение центров пунктов. Их количество, конструкция, а также методы закрепления выбираются в соответствии с требованиями и рекомендациями (ТКП 45-103-26-2006 (02250). Геодезические работы в строительстве. Правила проведения Минархстрой РБ, Минск, 2006, 66 с.). Также используются иные центры геодезических опорных сетей, хорошо себя зарекомендовавшие на других подобных объектах (см. рис. 3). Достоинством таких центров является возможность минимизации погрешностей за центрирование приборов и отражателя, а также возможность их закрепления вне зоны действия строительной техники (на элементах строительных конструкций).
Данные сети создаются как планово‑высотные с совмещенными центрами пунктов. Метод создания – линейно-угловое построение, возможно применение векторной многократной засечки в сочетании с методом «свободной станции».
Поскольку в процессе строительства по мере увеличения массы объекта могут происходить осадки и смещения фундаментов, для инженерно-геодезического обеспечения строительно-монтажных работ в качестве исходной геодезической основы служит опорная геодезическая сеть на нулевом горизонте, центры пунктов которой должны быть закреплены на элементах конструкций фундаментов строительных осей сооружения. По причине сложной геометрии строительных осей и элементов строительных конструкций на объекте их вынос в проектное положение рекомендуется производить координатным методом (проектные координаты контрольных точек выдаются проектной организацией).
При использовании электронных тахеометров с применением световозвращающих пленок центр марки обязательно должен быть зафиксирован из световозвращающего материала, например способом, показанным на рис 4.
По материалам доклада доктора технических наук профессора заведующего кафедрой инженерной геодезии БНТУ В. П. Подшивалова
Источник
РУП «Белстройцентр»
В статье предложен один из возможных методов определения продольной и поперечной ровности дорожного покрытия с использованием современных нивелиров и тахеометров. При использовании тахеометров для определения ровности предлагается метод свободной станции, который также может применяться при инженерно-геодезическом обеспечении дорожного строительства, ремонте и содержании автомобильных дорог.
This article describes one of the possible methods of estimating longitudinal and transverse evenness of the road pavement by using modern levels and tacheometers. When using tacheometers for estimation of the pavement evenness, a free station method is proposed. This can be also used for engineering and geodetic support of construction, maintenance and repair of roads.
ВВЕДЕНИЕ
Ровность дорожных покрытий является одной из важнейших характеристик эксплуатационного состояния автомобильных дорог. Для ее определения применяются различные методы. Среди них – как традиционные, так и с применением новых технических средств. К традиционным можно отнести методы, основанные на использовании измерительных мерных реек, виографов и толчкомеров, а к новейшим – анализаторы ровности, лазерные профилографы, сканирующие установки и др. В качестве показателей ровности используются величина и количество просветов под рейкой, суммарная амплитуда колебания неподрессоренных масс и др. (рис. 1).
Основным показателем ровности в последние годы в мировой практике признан Международный индекс ровности IRI (INTERNATIONAL REFNIS INDECS), который вошел в нормативные документы для оценки качества автомобильных дорог Беларуси. Разработаны и применяются на практике программы перевода различных показателей ровности в систему IRI и это позволяет использовать различные методы, унифицируя окончательные показатели состояния дорог по критерию ровности [1].
Одним из методов сбора первоначальной информации о ровности покрытия можно считать варьирования превышений поверхности покрытия, рассматриваемые в продольном и поперечном направлениях, а также по поверхности. Для этого целесообразно использовать методы нивелирования с применением современных приборов. Методы, основанные на нивелировании, по мнению авторов, предоставляют новые возможности для оценки ровности участков дорожного покрытия различной протяженности и геометрии вероятностно-статистическими методами. Ровность определяется относительно вероятнейших кривых, определенных вдоль дорожного покрытия по материалам нивелирования по методу наименьших квадратов.
Для продольной ровности выбирается линия на проезжей части дороги на расстоянии 0,5–1,0 м от края дорожного покрытия или полосы движения, вдоль которой намечают точки через 0,5 м для установки нивелирной рейки. Отсчеты по рейке производят с точностью до 1,0 мм. Длина исследуемого участка выбирается обоснованно с таким расчетом, чтобы полученные данные можно было считать репрезентативными при оценке рассматриваемого объема. Его длина может варьироваться в пределах от 100 до 2000 м в зависимости от геометрии участка автомобильной дороги.
По мнению авторов, однолинейное геодезическое измерение ровности не является достаточным. Как минимум, продольную ровность покрытия необходимо измерять по ряду параллельных продольных линий, по которым происходит взаимодействие колес подвижного состава с дорогой, а, следовательно, и его вертикальная динамика.
Для оценки поперечной ровности, в том числе и колейности, на полосе движения должны быть выбраны восемь точек: две – по полосам наката, четыре – на расстоянии 20–30 см по обе стороны от полос наката и две – по краям полосы движения. Точность нивелирования должна быть аналогичной, как и в продольном направлении.
При решении поставленной задачи будем иметь в виду, что реальная поверхность дорожного покрытия может иметь различную геометрию. В зависимости от рельефа местности и ситуации участки дороги могут состоять: из прямолинейных участков с поперечным и продольным уклонами; криволинейных участков с виражами и односкатными поперечными профилями. В связи с этим, задача может быть решена в два этапа: первый – восстановление геометрии участка дорожного покрытия (исполнительная съемка); второй – собственно, оценка ровности. На первом этапе производится определение длины исследуемого участка в зависимости от вида его геометрии.
ОБОСНОВАНИЕ МЕТОДА РЕШЕНИЯ ЗАДАЧИ
Автомобильная дорога может иметь различное число полос движения в одном направлении (рис. 2). На качество движения автотранспорта в основном влияет ровность отдельной полосы. Отдельная полоса движения имеет внутреннюю и внешнюю дорожную колею, которые в общем случае представляют собой некоторые пространственные кривые. Уравнения этих кривых должны быть одинаковы на прямолинейных участках дороги (отличие высотных отметок точек на одном поперечнике обусловлено только крутизной ската) и различаться на криволинейных участках (за счет вертикальных кривых на виражах). Следует иметь в виду, что возможны продольные уклоны, а также выпуклые и вогнутые формы дорожного полотна, вызванные рельефом местности.
Представим, что кривые могут быть описаны уравнением параболы
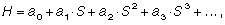
где H – высотная отметка;
ai – коэффициент положительный и отрицательный (параметры параболы);
S – расстояние вдоль оси обследуемого участка трассы.
Степень данного уравнения зависит от геометрии участка трассы, например, на прямолинейных горизонтальных участках трассы коэффициенты ai (i = 2, 3, …) будут стремиться к нулю, и уравнение описывает прямую линию. Чем выше степень уравнения, тем сложнее по форме кривую оно описывает. Учитывая требования к проектированию и строительству дорог, по мнению авторов, достаточно ограничиться третьей степенью в уравнении (1).
В соответствии с ранее оговоренными требованиями, на поперечниках каждой полосы движения должны быть выбраны восемь точек (рис. 3). Следовательно, будут иметь место 8 уравнений вида (1). В этом случае выбирают четыре равномерно расположенные точки вдоль каждой из исследуемых линий, две из которых располагают вначале и конце обследуемого участка. Возможные варианты продольных профилей обследуемых участков дороги приведены на рис. 4.
Для каждой исследуемой линии получают по четыре уравнения вида:
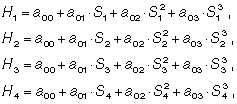
где a0j – приближенное значение коэффициента (параметра кривой);
Hj+1 – измеренная высотная отметка вдоль трассы на расстоянии Si+1 соответственно (j = 0, 1, 2, 3).
Система уравнений (2) линейна относительно искомых параметров aj, решая которую находят их приближенные значения. Вдоль исследуемой линии производят большее число измерений (через расстояния, определенные категорией дороги или техническими условиями). Пусть таких измерений произведено n > 4. В этом случае получают неопределенную систему уравнений:
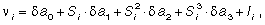
n i – уклонение от измеренных отметок Hi (собственно, неровности);
d ak – поправка к приближенным значениям параметров кривой (k = 1, 2, 3, 4).
Возникает вопрос решения неопределенной системы n уравнений (3), содержащей (n + 4) неизвестных. Здесь целесообразно находить такие значения параметров кривой, при которых уклонения n i будут носить случайный характер. Это будет иметь место, если систему (3) решать при условии
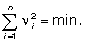
Решение задачи, как видим, сводится к нахождению экстремума квадрата функций (3) и применению метода наименьших квадратов. В результате вычисления производных от квадратов функций (3) и приравнивания их к нулю, приходят к системе нормальных уравнений, в которой число уравнений равно числу искомых поправок d ak:
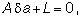
где 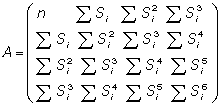
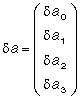
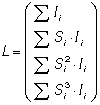
После решения системы уравнений (5) определяются вероятнейшие поправки к приближенным значениям параметров кривой, аппроксимирующей продольный профиль полосы движения дороги. Вероятнейшие значения параметров кривой (1) находят из уравнений:
Из уравнений (3) получаются искомые величины неровностей. Точность их определения может характеризоваться средней квадратической ошибкой
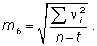
Предлагаемая методика получения вероятнейших выражений для уравнений кривых вида (1) позволяет получить объективные данные, характеризующие профиль дорожного покрытия вдоль линий трассы. Если обследуются восемь линий на дорожном покрытии, аналогичным путем получают восемь уравнений:
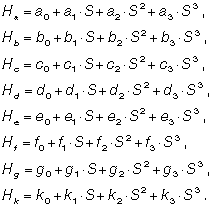
Таким образом, получаем данные для оценки ровности дорожного покрытия на основе вероятностно-статистических методов. При необходимости из уравнений (7) можно получить значения высотных отметок на любом поперечнике, для конкретного значения S, по которым можно оценивать состояние поперечных уклонов, виражей. По мнению авторов, такая методика представляет интерес для оценки качества строительства и эксплуатационного состояния дорог, дает достаточно информации для определения соответствия дорожного покрытия категории дороги, требуемому скоростному режиму и уровню содержания.
Исполнительная съемка при этом производится по поперечникам, которые разбивают через 5–10 м на прямолинейных участках и на кривых. На каждом поперечнике определяют планово-высотное положение указанных ранее восемь точек.
Для однозначного определения параметров параболы (1) необходимо иметь четыре значения H вдоль каждой полосы движения. Как известно, любые измерения сопровождаются ошибками, дорожное покрытие может иметь особенные точки. Поэтому вероятнейшие значения параметров уравнения (1), а, следовательно, вероятнейшие величины отметок дорожного покрытия (при отсутствии неровностей) находят из уравнений, полученных по рассмотренной методике. При этом число поперечников, на которых произведены измерения, может быть существенно меньше, чем число поперечников, исследование которых возможно на основе полученных математических моделей. Выбор числа поперечников зависит от состояния проезжей части и требуемой точности диагностирования ровности.
Для расчета необходимой точности геодезических измерений принимаются параметры необходимой точности строительно-монтажных работ, представленные в проекте. Уравнение (6) позволяет планировать количество точек на кривой n, точность нивелирования.
ПРОИЗВОДСТВО ИЗМЕРЕНИЙ
Наиболее простым методом определения высотных отметок дорожного покрытия может служить метод геометрического нивелирования поперечников. На дорожном покрытии выбирается некоторая точка, отметка которой может быть определена от исходного репера или иметь какое-либо условное значение. При этом нивелир устанавливается в точке, с которой виден исследуемый участок дороги. Если это невозможно по условиям местности, исследуемый участок дороги может разбиваться на несколько частей. Нивелирная рейка последовательно устанавливается на каждой из восьми точек на равноудаленных поперечниках (через 5–10 м), получают значения отметок. Таких значений будет 8n при обследовании восьми линий. На каждой линии выбирают по четыре точки (всего их будет 32), по значениям отметок которых вычисляют приближенные значения параметров парабол из уравнений вида (2). Далее действуют по ранее приведенному алгоритму.
Учитывая, что для решения поставленной задачи требуется большой объем измерений, целесообразно применять современные приборы. Наибольший эффект, по мнению авторов, можно получить, применяя цифровые нивелиры с компенсаторами в комплекте с кодовыми рейками. В этом случае автоматизируется процесс снятия, запоминания и хранения в памяти прибора отчетов по рейке, определяется расстояние до рейки, а также учитывается влияние несоблюдения главного условия нивелира при неравных значениях расстояний от нивелира до рейки (неравенство плеч). Можно также применять ротационные лазерные нивелиры. Такие нивелиры выпускают зарубежные фирмы TRIMDLE, LEICA и др. На территории Республики Беларусь имеются официальные представители этих фирм, у которых можно приобрести приборы.
По мнению авторов, также заслуживает внимания метод тригонометрического нивелирования с применением электронных тахеометров производства фирм TRIMDLE, LEICA и др. Следует заметить, что эти тахеометры всего точностного ряда оснащены стандартными пакетами программ для ЭВМ, встроенных в прибор и позволяющих в автоматическом режиме решать самые разнообразные задачи. Эффективность применения тахеометров существенно возрастает с использованием специальных пакетов программ для ЭВМ.
Электронный тахеометр реализует пространственную линейно-угловую (векторную) засечку, в которой передаются не только высотные, но и плановые координаты. Наибольший эффект при работе электронным тахеометром получают при работе методом «свободной станции». Смысл данного метода заключается в возможности работы тахеометра в двух режимах. Первый режим – координирование и ориентирование прибора от исходных пунктов, координаты которых предварительно занесены в электронную память прибора. Для того чтобы измерения горизонтальных, вертикальных углов и расстояний, а также вычисления координат выполнить с контролем, измерения должны производиться не менее, чем на четыре исходных пункта. Второй режим – съемка, при которой находятся координаты определяемых точек или выносятся точки, проектные координаты которых предварительно внесены в электронную память прибора.
При соответствующей системе нумерации исходных пунктов, а также определяемых точек электронная база прибора хранит всю полноту информации об измерениях, а также координатах исходных пунктов и координатах определяемых точек. Эти данные могут при необходимости передаваться посредством электронной связи.
Приращения координат D x, D y и превышения D h определяемых точек относительно геометрического центра прибора вычисляются по следующим формулам:
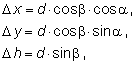
где d – измеренное наклонное расстояние;
a – дирекционный угол;
b – измеренный вертикальный угол.
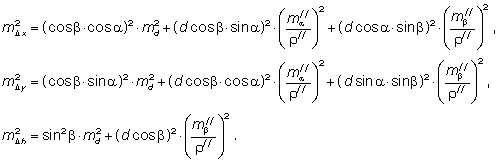
Здесь a и b – дирекционный и вертикальный углы засечки, d – измеренное расстояние, а также их средние квадратические ошибки, зависящие от класса точности прибора. Под средней квадратической ошибкой дирекционного угла здесь понимают среднюю квадратическую ошибку измерения горизонтальных углов.
Для расчета точности векторной засечки (при планировании измерений) можно применять формулы, идентичные формулам (9), выражающие соответствующие относительные средние квадратические ошибки:
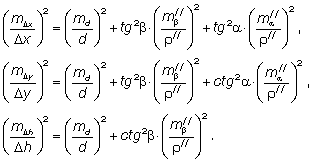
Если требуется определить класс точности приборов и методику измерений при определении планово-высотного положения точек на исследуемых линиях регламентируемой точности, применяют к формулам (10) принцип равных влияний (11):
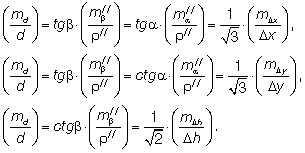
Исходя из реальных условий на объекте, следует учесть наихудшие геометрические параметры засечки, которые могут иметь место. Местоположение свободной станции определяется из соображений обеспечения наивыгоднейших условий для производства измерений.
В случае тригонометрического нивелирования и реализации векторной засечки электронным тахеометром следует иметь в виду, что помимо приборных погрешностей измерения расстояний, вертикальных и горизонтальных углов будут иметь место погрешности наведения на марку или наклон вехи отражателя, расположенного на некоторой высоте вехи H над контрольной точкой (рис. 5). В комплект к тахеометрам входят вехи длиной до 3 м. Отражатель крепится к специальной вехе, имеющей фиксированную и известную длину. В вертикальное положение веха устанавливается с помощью круглого уровня, имеющего определенную точность b (обычно 120–300″).
Приведем расчет погрешности в превышении за наклон мини-вехи. Из рис. 5 видно, что погрешность в измеренном превышении D h, обусловленная наклоном мини-вехи, составит величину, вычисляемую из выражения
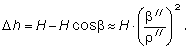
Несложно рассчитать, что данная погрешность практически незначительна. Следовательно, здесь возможно применение отражателя с большой вехой. При этом следует обратить внимание на то, что данные условия влияют и на точность планового определения ?Р. Согласно рис. 5, ?Р определяется по формуле
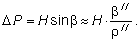
При использовании вехи и отражателя необходимо иметь в виду эти погрешности и устранять их. На основании расчетов, произведенных по формулам (11)–(13), выбираются класс точности прибора, методика измерений, допустимая длина вехи, в обязательном порядке поверяется круглый уровень.
Следует отметить, что погрешность за наклон вехи отражателя в приращения плановых координат существенно больше по сравнению с погрешностью в превышение. Например, если принять H = 3000 мм, b = 300″, то получим соответственно: ?h = 0,7 мм; ?P = 4,5 мм. Зная точность круглого уровня, входящего в комплект отражателей, и необходимую точность определения превышений и приращений координа, можно рассчитать допустимые высоту вехи и ее наклон.
МЕТОД СВОБОДНОЙ СТАНЦИИ
По мере развития геодезического приборостроения существенно расширяются возможности совершенствования технологий инженерно-геодезического производства, направленные на автоматизацию измерительных процессов, оптимизацию геодезических построений, безбумажные методы записи, хранения и передачи на математическую обработку измерительной информации, все возрастающие возможности выдачи геодезических данных потребителям в режиме реального времени [3].
В инженерно-геодезическом обеспечении дорожного строительства большой проблемой является сохранность центров геодезических пунктов как опорной, так и разбивочных сетей. В специальной литературе по геодезическому обеспечению дорожного строительства этот метод не излагается, поэтому авторы считают необходимым в краткой форме пояснить его сущность. Отличие этого метода заключается в том, что прибор в процессе измерений устанавливается не над центром исходного или определяемого геодезического пункта, а в некоторой точке, положение которой оптимально для координирования и ориентирования прибора, а также для передачи координат и высот на контрольные точки.
Приведем схему работы в режиме свободной станции (рис. 6). Следует иметь в виду, что в режиме свободной станции электронным тахеометром можно работать в пространственной системе координат (совмещенные плановая и высотная сети – векторная сеть). Измерения могут вестись как с отражателем на специальную пленку, так и в безотражательном режиме, в зависимости от условий решаемой задачи.
Для однозначного (бесконтрольного) определения планово-высотного положения геометрического центра прибора и его ориентировки в принятой системе координат достаточно произвести позиционирование на два исходных пункта, планово-высотные координаты которых известны. Измеряются: две наклонные дальности, один горизонтальный и два вертикальных угла. В современных тахеометрах зарубежных фирм-производителей имеется соответствующее встроенное программное обеспечение, позволяющее работать в различных режимах. На данном этапе следует работать в режиме «координирование прибора».
Если по каким-либо причинам стандартным программным обеспечением прибора воспользоваться невозможно, решение задачи также можно обеспечить. Приведем сущность решения этой задачи (рис. 7). Здесь известны плановые координаты и высоты (отметки) двух пунктов А и Б: Xa, Ya, Ha, Xb, Yb, Hb. Измерены наклонные дальности Sa, Sb, их горизонтальные направления, по разности которых вычисляют горизонтальный угол Bab; также измерены вертикальные углы b A, b Б.
Вычисляют горизонтальные направления по известной формуле
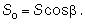
Из решения обратной геодезической задачи вычисляют горизонтальные направления между центрами исходных пунктов и дирекционные (прямой и обратный) углы:
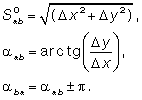
Значение дирекционного угла определяют по знакам приращений координат, как это принято при решении обратной геодезической задачи.
Из решения треугольника А0Б0С по теореме синусов вычисляются его горизонтальные углы при вершинах А0 и Б0:
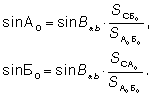
Наличие одной избыточной величины в треугольнике позволяет провести контроль измерений и вычислений, вычислив невязку в треугольнике:
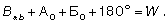
Дирекционные углы направлений вдоль измеренных наклонных дальностей вычисляют по формулам:
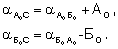
Приращения координат от любой исходной точки до центра прибора определяются по формулам решения прямой геодезической задачи. Они имеют вид:
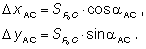
Координаты центра прибора в этом случае будут равны:
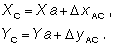
Ориентировкой угломерной шкалы горизонтального круга служат дирекционные углы сторон СА и СБ.
Высотная отметка центра прибора определяется с контролем от двух исходных пунктов по превышениям, получаемым из тригонометрического нивелирования:
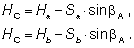
В современных электронных тахеометрах все эти вычисления ведутся в автоматическом режиме, запоминаются и могут быть использованы в дальнейшей работе. Опыт работы на реальных объектах показывает, что координирование и ориентирование центра прибора указанным методом необходимо производить от трех и более исходных пунктов. В этом случае прибор дает не только искомые величины, но и ошибки их определения. Более трех исходных пунктов берут в случаях, когда имеет место изменение планово-высотного положения центров исходных пунктов и необходимо произвести анализ их стабильности.
Произведя координирование и ориентирование прибора, приступают (в режиме «съемка») к координированию контрольных точек. С одной таким образом определенной свободной станции можно производить координирование и разбивку любого числа видимых точек. В реальных условиях таких свободных станций на объекте может быть любое, достаточное для работы число. Для обеспечения необходимой и однородной точности координатных определений, производства уравнительных вычислений и оценки точности результатов измерений на каждой свободной станции измерения производят с перекрытием.
ВЫВОДЫ
На основании приведенного выше анализа существующей проблемы по определению ровности покрытия и теоретических исследований можно сделать следующие выводы.
1 Традиционные методы определения ровности дорожного покрытия не в полной мере отражают состояние дорожного покрытия.
2 Предлагаемая методология, основанная на результатах нивелирования и вероятностно-статистическом методе аппроксимации, может давать достаточную информацию о геометрии дорожной полосы и ровности дорожного покрытия, а также для определения международного индекса ровности (IRI).
3 Использование цифровых нивелиров и электронных тахеометров позволит обеспечить необходимую точность, существенно снизить трудоемкость и повысить производительность полевых работ.
4 Метод свободной станции, реализуемый при работе с электронным тахеометром, может давать значительный эффект, как для определения ровности дорожного покрытия, так и при геодезическом обеспечении строительства автомобильных дорог.
СПИСОК ЛИТЕРАТУРЫ
1. Леонович, И. И. Диагностика автомобильных дорог / И. И. Леонович, С. В. Богушович, И. В. Нестерович. – М.: ИНФРА, 2011. – 350 с.
2. Нестерович, И. В. Критерии ровности асфальтобетонных дорожных покрытий и их использование при оценке эксплуатационного состояния автомобильных дорог: автореф. … дис. канд. техн. наук / И. В. Нестерович. – Минск, 2004 – 23 с.
3. Подшивалов, В. П. Особенности инженерно-геодезического обеспечения строительства / В. П. Подшивалов, В. В. Ялтыхов, А. И. Козакевич // Архитектура и строительство. – 2009. – С. 22–26.
Источник