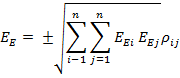Математическая энциклопедия
СУММИРОВАНИЯ МЕТОДЫ
СУММИРОВАНИЯ МЕТОДЫ — способы построения обобщенных сумм рядов, обобщенных пределов последовательностей, значений несобственных интегралов.
В математич. анализе возникает потребность обобщить понятие суммы ряда (предела последовательности, значения интеграла) на случай, когда в обычном смысле ряд (последовательность, интеграл) расходится. Такое обобщение задают обычно в виде нек-рого правила или операции и называют методом суммирования.
1) Ряд Фурье непрерывной 



равномерно сходится на всей оси Ох к функции f(х), Если сумму ряда определить как

то в этом смысле ряд Фурье 

полученный в результате умножения двух рядов

сходящихся соответственно к Аи В, может оказаться расходящимся. Если сумму ряда (2) определить, как в примере 1), т. е. как предел последовательности средних арифметических первых пчастичных сумм, то в этом смысле произведение указанных рядов будет сходиться к сумме С=АВ.
3) Степенной ряд

сходится для |z|

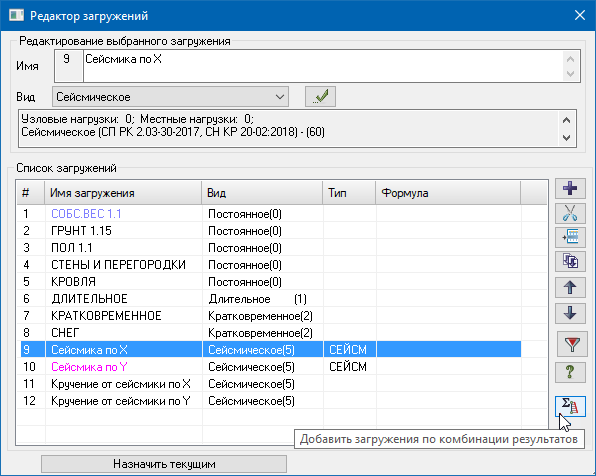
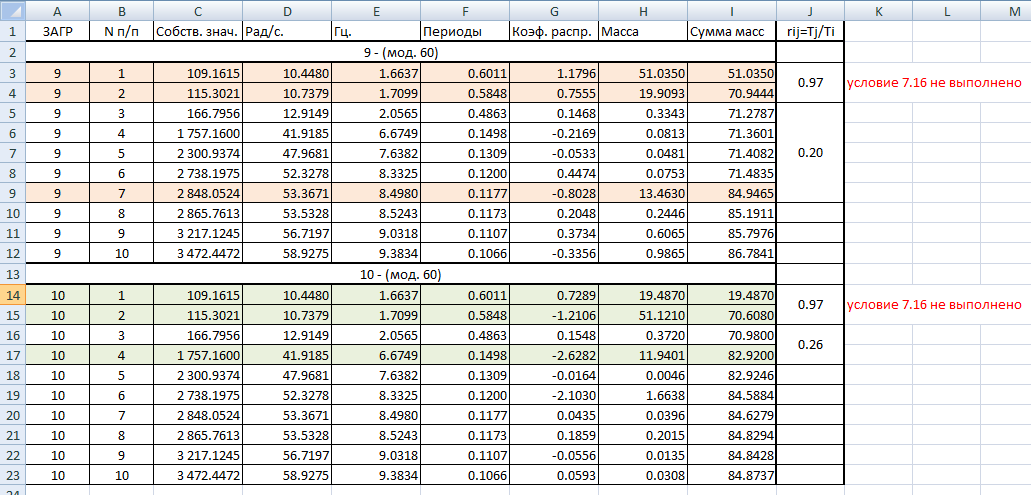
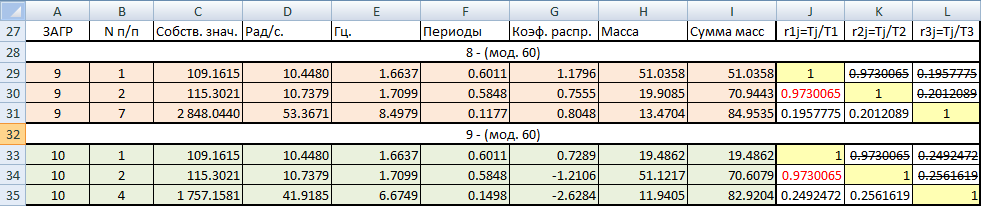
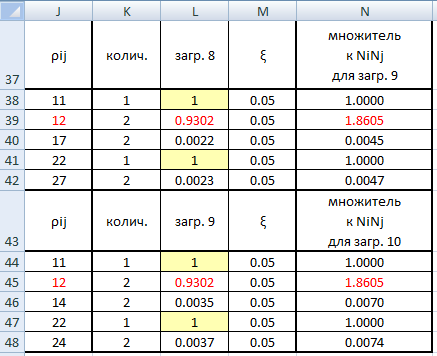
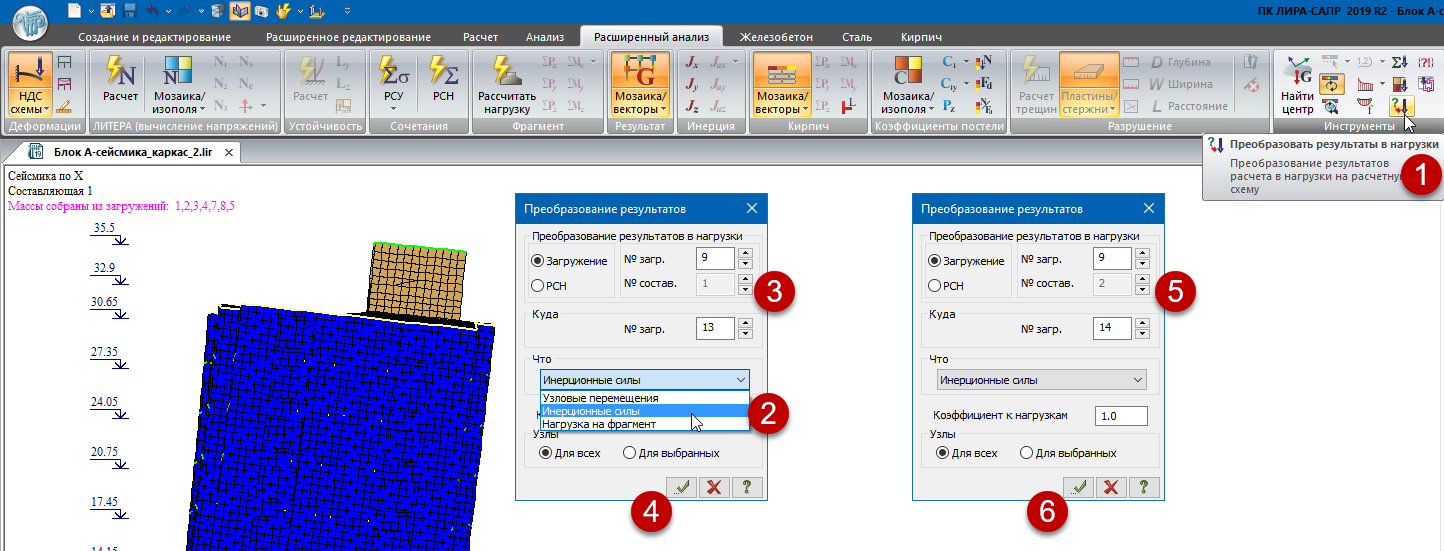
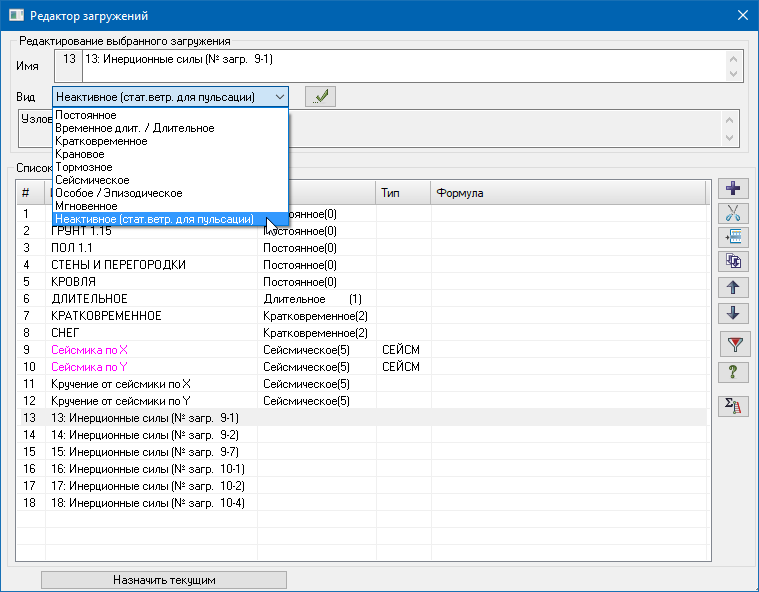
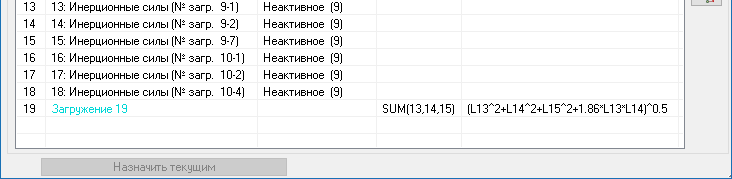
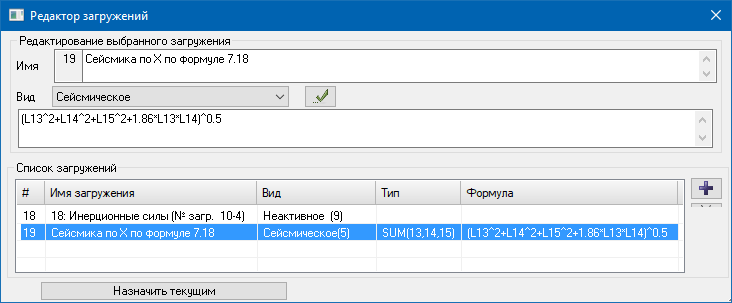
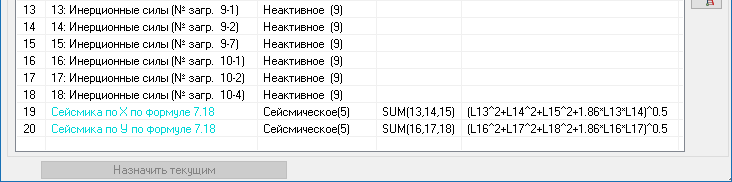
где sn — частичные суммы ряда (3), то в этом смысле ряд (3) будет сходиться для всех z, удовлетворяющих условию Rez Важнейшими свойствами С. м. являются регулярность (см. Регулярные методы суммирования )и линейность (см. Линейный метод суммирования). Наиболее распространенные С. м. обладают этими свойствами. Многие из методов обладают также свойством транслятивности (см. Транслятивность метода суммирования). Широкий класс С. м. составляют матричные методы суммирования и полунепрерывные методы суммирования. Эти методы являются линейными и для них установлены условия регулярности. К матричным С. м., в частности, относятся Вороного метод суммирования, Чезаро методы, суммирования. Подкласс матричных С. м. составляют методы, определенные конечнострочными матрицами (см. Конечнострочный метод суммирования) и в частности треугольными матрицами (см. Треугольный метод суммирования). Полунепрерывными методами суммирования являются Абеля метод суммирования, Бореля метод суммирования, Миттаг-Леффлера метод суммирования, Линделёфа метод суммирования, Рисса метод суммирования. Существуют С. м., не относящиеся к указанным видам, напр. интегральный метод суммирования Бореля, Гёльдера методы суммирования. Одна и та же последовательность (ряд) может быть суммируема одним методом и не суммируема другим. Множество всех последовательностей (рядов), суммируемых данным методом, наз. суммируемости полем данного метода. Если рассматривают два С. м., и поле суммируемости одного метода содержит поле другого метода, то говорят о включении методов суммирования;в случае совпадения полей говорят о равносильности методов суммирования. Если поле С. м. состоит только из сходящихся последовательностей, то говорят, что С. м. эквивалентен сходимости. Установление условий, при к-рых имеет место включение С. м., является одной из задач теории суммируемости. Два или несколько С. м. могут быть совместными и несовместными. С. м. наз. совместными методами суммирования, если они не могут суммировать одну и ту же последовательность к различным пределам. В тех случаях когда из суммируемости ряда методом Авсегда следует суммируемость ряда методом В, говорят, что числа Относительно С. м. различают два типа теорем. В теоремах 1-го (абелевого) типа из свойств последовательности делают заключение о свойствах средних этой последовательности, полученных в результате преобразования, определяющего С. м. Напр., теорема Коши, устанавливающая, что из По аналогии с обычной сходимостью вводят понятия специальных видов суммируемости: абсолютной суммируемости, безусловной суммируемости, сильной суммируемости, почти-суммируемости, Понятие обобщенного предела вводят также для функций и интегралов. В этих случаях говорят о суммировании функции (соответственно интеграла). Напр., для функции s(y), определенной для всех у, С. м., аналогичный матричному С. м. последовательностей, состоит в том, что рассматривается интегральное преобразование типа с ядром с( х, у), и функции s(y) в качестве ее обобщенного предела при Аналогично, один из С. м. несобственных интегралов состоит в том, что рассматривают преобразования с ядром К( х, t),n интеграл (4) называют суммируемом к значению s, если Определение С. м., введенное для суммирования числовых и функциональных последовательностей, обобщается на последовательности из элементов любого множества и общее определение С. м. может быть сформулировано так: пусть X — заданное множество, s(X) — множество последовательностей Лит.:[1] Харди Г., Расходящиеся ряды, пер. с англ., М., 1951; [2] Кук Р., Бесконечные матрицы и пространства последовательностей, пер. с англ., М., 1960; [3] Кангро Г. Ф., в сб.: Итоги науки и техники, Математический анализ, т. 12, М., 1974, с. 5-70; [4] Барон С., Введение в теорию суммируемости рядов, Таллин, 1977; [5] Реуеrimhoff A., Lectures on summability, В.- Hdlb.- N. Y., 1969; [6] Кnоpp K., Theory and application on infinite series, L., 1966; [7] Zeller K., Beekmann W., Theorie der Limitierungsverfahren, 2 Aufl., В.-Hdlb.-N. Y., 1970; [8] Pitt H., Tauberian theorem’s, L., 1958; [9] Gane1ius Т. H., Tauberian remainder theorems, В.-[а. о.], 1971; [10] Petersen G. M., Regular matrix transformations, N. Y.-Toronto-Sydney, [1966]; [11] Брудно А. Л., лМатем. сб. Источник Суммирование форм CQC по формуле 7.18 СП РК 2.03-30-2017 в ЛИРА-САПР 2019R2 Чтобы реализовать суммирование форм по формуле 7.18 (СП РК 2.03-30-2017) при несоблюдении условия 7.16 (отношение периодов форм более 10%) во втором релизе версии Лира-САПР 2019 можно в «Редакторе загружений» воспользоваться новой функцией «Добавить загружение по комбинации результатов». Для этого нужно сделать расчет схемы с заданным сейсмическим воздействием. Получить периоды колебания и сбор модальных масс. Оценить отношение периодов тех форм, чей вклад в модальную массу более 5% (см. п. 7.8.2 СП РК 2.03-30-2017). Рассмотрим на конкретном примере полученную таблицу «Периоды колебаний»: В соответствии с формулой 7.18 мы должны составить такую новую сумму отдельных форм: На примере с тремя формами мы получим под корнем такое произведение: ρ11 N1N1 + ρ12 N1N2 + ρ13 N1N3 + ρ12 N2N1 + ρ22 N2N2 + ρ23 N2N3 + ρ13 N3N1 + ρ23 N3N2 + ρ33 N3N3 = Здесь: Сделаем вычисления коэффициентов к произведению форм в Excel, приняв величину демпфирования ξ равную 0.05 (см. п. 3.33 СП РК 2.03-30-2017): Теория (в исходном тексте СП РК 2.03-30-2017 в формуле 7.19 в знаменателе потерян квадрат): Для начала получим коэффициенты rij (учитывая, что мы всегда делим меньшую величину периода на большую): Далее по формуле 7.19 получаем множители к произведению форм с неодинаковыми номерами: Исключим из внимания множители менее 0.05 (ме6нее 5% от произведения разных форм), как несущественные. Получается, что нам нужно к сумме квадратов форм добавить одно произведение форм 1 и 2 (отношение периодов которых как раз было менее 10%). В итоге мы должны получить следующую комбинацию форм: (N1^2+N2^2+N3^2+ ρ12 N1N2)^0.5 = (N1^2+N2^2+N3^2+ 1.86 N1N2)^0.5 В формуле выше для загружения 9 (сейсмика по Х) N3 – это форма 7, для загружения 10 (сейсмика по У) N3 – это форма 4, т.е. это ближайшие формы давшие вклад в модальную массу более 5%. Теперь, в уже посчитанной ранее задаче, нам нужно из форм колебаний 1, 2 и 7 для загружения 9, и 1, 2 и 4 для загружения 10 передать в исходные данные полученные инерционные силы. Для этого мы: После копирования нужных форм сохраняем задачу с другим именем, чтобы не потерять ранее рассчитанную задачу (на всякий случай). В исходных данных в «Редакторе загружений» видим новые загружения, с именами полученными автоматически, и для них указываем и применяем вид «Неактивное», поскольку эти загружения отдельно сами по себе нигде в комбинациях, в данном случае, участвовать не будут: Нажимаем новую кнопку «Добавить загружения по комбинации результатов»: Получаем диалог суммирования по формуле, в котором выбираем «Произвольная» и вводим формулу суммирования новых загружений с инерционными силами, как узловыми нагрузками: (L13^2+L14^2+L15^2+ 1.86 *L13*L14)^0.5 где: В итоге получили новое загружение 19: Поменяем вид загружения (на «сейсмика») и название: Повторим то же самое для загружений 16-18: В комбинациях РСУ (и РСН, если нужно) задаем параметры этих новых загружений «с сейсмикой» по Х и У точно такие же, как задавали для исходных «сейсмики по Х (по У)» в загружениях 9 и 10 (из которых мы копировали формы), только добавляем номер группы взаимоисключения между этими загружениями, чтобы «сейсмика по Х (по У)» не была учтена дважды. В данном случае предлагаем не исключать из комбинаций нагрузок сейсмику с суммированием форм полученной как корень квадратный из суммы квадратов (привычным способом), чтобы получить худший результат из обоих способов суммировнаия. Обратите внимание на рисунок ниже – в новом загружении 20 «Сейсмика по У по формуле 7.18» задали все те же параметры, что были заданы для загружения 10 «Сейсмика по Y»: знакопеременность, сопутствие загружения 12 (кручение от сейсмики по У), коэффициент сочетания 0.3 в столбце 3 (особое сочетание с сейсмикой), коэффициент сочетания 1 в столбце 7 (особое сочетание с сейсмикой), только добавился номер группы взаимоисключений 3 (между собой, между загружением 10 и 20). Источник




















Суммирование форм CQC по формуле 7.18 СП РК 2.03-30-2017
ρ11 N1^2 + ρ22 N2^2 + ρ33 N3^2 + 2* ρ12 *N1*N2 + 2* ρ13 * N1*N3 + 2* ρ23 * N2*N3
— произведения N1N2 и N2N1 одинаковы, поэтому получаем «2* ρ12 *N1*N2 »;
— коэффициенты ρii к произведению форм самих на себя (ρ11, ρ22, …) по формуле 7.19 равны 1.
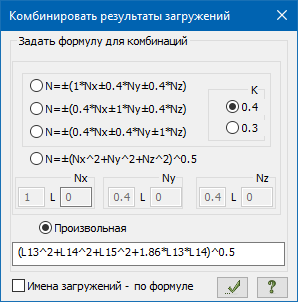
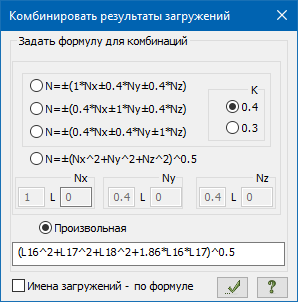
L13 – усилия загружения 13, L14 – усилия загружения 14 и т.д.;
1.86 – коэффициент ρ12 посчитанный в Excel;
(…)^0.5 – корень квадратный (все, что в скобках в степени 1/2).