- Геодезия
- Разделы
- Определение веса измеряемых величин
- Неравноточные измерения в геодезии
- Определение неравноточных измерений производимых не в одинаковых условиях с различными дисперсиями и средними квадратическими погрешностями. Вычисление среднего весового значения или арифметической средины квадратической погрешности измерений угла.
- Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Геодезия
Для студентов аспирантов и преподавателей
Разделы
- Сила тяжести и уровенные поверхности земли
- Геоид и квазигеоид
- Общий земной эллипсоид
- Нормальная земля и фигура реальной земли
- Референц-эллипсоид Красовского
- Координаты и азимуты
- Уклонения отвесных линий
- Азимуты лапласа
- Понятие о редукционной задаче
- Геодезические сети и их назначение
- Основной принцип построения геодезической сети
- Плотность пунктов государственной
- Необходимая точность построения ггс
- Основные методы создания ггс
- Сведения о других методах создания ггс
- Опорные геодезические сети в дореволюционной России
- Схема и программа Ф.Н. Красовского построение государственной триангуляции
- Государственная геодезическая сеть в СССР
- Последовательность выполнения основных геодезических работ
- Пути cовершенствования ггс
- Общие сведения о проектировании ггс
- Рекогносцировка геодезических пунктов
- Расчет высоты геодезических знаков
- Геодезические знаки
- Центры геодезических пунктов
- Априорная оценка точности геодезических сетей
- Определение веса измеряемых величин
- Вычисление обратного веса уравненных элементов
- Априорная оценка точности ггс с моделированием результатов измерений на компьютере
- Оценка точности триангуляции
- Оценка точности рядов и сетей трилатерации по приблеженным формулам
- Оценка точности звеньев полигонометрии
- Согласование точности измерения горизонтальных направлений, азимутов и длин сторон в геодезических сетях
- Условия эксплуатации высокоточных теодолитов
- Общие сведения о высокоточных теодолитах
- Геометрическая схема высокоточного теодолита
- Осевые системы и уровни теодолита
- Лимб высокоточного оптического теодолита
- Зрительные трубы высокоточных теодолитов
- Отсчетное устройство оптического теодолита
- Принцип совмещенного отсчета
- Поверки и исследования высокоточных теодолитов
- Определение рена оптического микрометра
- Погрешности шкалы оптического микрометра
- Определение эксцентриситета алидады и лимба
- Отдельное спасибо
- return_links(2); ?>
Определение веса измеряемых величин
Достоверность и точность уравненных элементов геодезической сети во многом зависит от правильности установления реального веса каждой измеряемой величины. В общем случае вес каждой непосредственно измеренной величины должен вычисляться по формуле
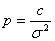
где с — постоянная для сети безразмерная величина (c=const), устанавливаемая до некоторой степени произвольно; 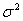
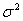
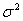
На стадии проектирования средние квадратические ошибки т измеряемых величин задают с учетом имеющегося опыта измерений таких величин в ранее построенных геодезических сетях. В этом случае вес запланированных к измерению в проектируемой сети горизонтальных направлений N, азимутов а, расстояний s вычисляют по формулам
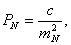
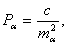
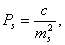
Горизонтальные направления на пунктах геодезической сети каждого данного класса измеряются равноточно. Поэтому целесообразно принять с=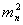
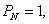
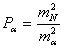
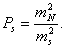
Средние квадратические ошибки измеренных направлений, азимутов, длин сторон можно найти разными способами и получить соответственно разные значения ошибки для одной и той же величины. Например, ошибку измеренного угла в триангуляции можно найти из уравнивания угловых измерений на станции (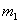
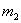
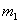
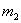
Известно, что совокупное влияние случайных и систематических ошибок на результаты измерений однородных величин наиболее полно сказывается на величинах свободных членов условных уравнений. Поэтому, чтобы получить средние квадратические ошибки, характеризующие реальную точность измерений, следует использовать невязки (свободные члены) условных уравнений.
В триангуляции среднюю квадратическую ошибку измеренного угла вычисляют по невязкам треугольников, используя формулу Ферреро
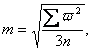
где п — число невязок со треугольников;
средняя квадратическая ошибка измеренного направления равна
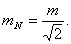
Для определения 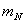
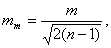
где п — число измерений, т. е. невязок треугольников в данном случае.
При свето- и радиодальномерных измерениях расстояний среднюю квадратическую ошибку 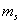
где а0 и а1 — эмпирические коэффициенты. Они указываются в паспорте прибора, а определяются из обработки измерений расстояний разной длины на эталонном полигоне. Однако практика показывает, что реальная точность измерений расстояний далека от величины, получаемой по формуле (5.9).
Наиболее достоверное значение средней квадратической ошибки измерения расстояний в сетях трилатерации и в линейно-угловых сетях можно вычислить по свободным членам со условных уравнений центральных систем и геодезических четырехугольников с измеренными в них длинами сторон:
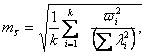
где 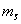
средней длины 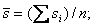
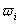
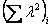
Если известны 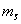
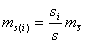
Формулы (5.10) и (5.11) дают несравненно более точные результаты, чем формула (5.9), поэтому их следует применять при вычислении по формулам (5.4) или (5.5) веса измеренных сторон.
Среднюю квадратическую ошибку определения астрономических азимутов на пунктах Лапласа вычисляют обычно по отклонениям значений азимута в приемах от его среднего значения. Величина полученной таким образом ошибки 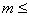
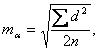
где п — число разностей d; в среднем тa =1,0″, что достаточно хорошо согласуется с другими оценками, полученными, например, при уравнивании обширных блоков астрономо-геодезической сети ( тa 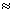
Вопросы надежной оценки точности измерений каждой базисной стороны и каждого азимута на пунктах Лапласа (не по сходимости результатов измерений в приемах) нуждаются в дальнейшем изучении и решении.
Источник
Неравноточные измерения в геодезии
Определение неравноточных измерений производимых не в одинаковых условиях с различными дисперсиями и средними квадратическими погрешностями. Вычисление среднего весового значения или арифметической средины квадратической погрешности измерений угла.
| Рубрика | Геология, гидрология и геодезия |
| Вид | практическая работа |
| Язык | русский |
| Дата добавления | 28.10.2017 |
| Размер файла | 29,6 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
1. ОБЩИЕ СВЕДЕНИЯ
2. ОБРАБОТКА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
3. РЕШЕНИЕ ЗАДАЧ
1. ОБЩИЕ СВЕДЕНИЯ
Неравноточными называют измерения производимые не в одинаковых условиях с различными дисперсиями, и средними квадратическими погрешностями.
2. ОБРАБОТКА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
При обработке неравноточных измерений вводят новую характеристику точности измерения, называемую весом измерения:
где k произвольно выбранное число, единое для всех весов, участвующих в решении задачи; д дисперсия результата измерения.
Так как точное значение никогда не известно, вес принимают:
где m -средняя квадратическая погрешность, по результам измерений.
Так как k произвольное число, то вес дает представление о точности результата только при сравнении его с весами других результатов.
1 Свойство весов: Отношение весов не изменяется, если все веса увеличить или уменьшить в одно и то же число раз.
2 Свойство весов:
Веса двух измерений обратно пропорциональны квадратам средних квадратических погрешностей этих измерений.
Из определения веса следует, что равноточные измерения имеют равные веса, а неравноточные — неравные веса. Приняв вес одного измерения за единицу, т. е. p = 1, вес среднего арифметического становится равным числу измерений P=n.
Если известны веса аргументов функции, то можно найти и вес самой функции. При k=1 вес р равен , откуда. Величину называют обратным весом.
Среднее весовое значение или арифметическая средина вычисляется:
а с приближенными значениями эта формула имеет вид:
В случае, когда из результатов измерений получено среднее весовое значение, вводят поправки: х=L.
Средняя квадратическая погрешность единицы веса через вероятнейшие поправки:
Средняя квадратическая погрешность общей арифметической средины имеет вид: , выражение средней квадратической погрешности общей арифметической средины через вероятнейшие поправки:
Средняя квадратическая погрешность единицы веса, если в разностях нет систематической погрешности:
В случае их наличия они исключаются из разностей. Систематическая погрешность обозначается И и определяется по формуле:
При расчете двойных линейных измерений, если в разностях нет И, средняя квадратическая погрешность единицы веса:
если она имеется, то
3. РЕШЕНИЕ ЗАДАЧ
Произвести обработку результатов ряда неравноточных измерений. Найти среднюю весовую и среднюю квадратическую погрешность средневесового. неравноточный угол погрешность весовой
Таблица 1. Результаты обработки ряда неравноточных измерений угла
Источник





