Уравнивание теодолитного хода как неотъемлемая часть геодезических работ
Основная цель уравнивания состоит в оценке точности выполненных на натуре измерений. Вычисленные невязки сравнивают с предельно допустимыми, что и позволяет определить, соответствует ли их значение нормативным требованиям.
Впоследствии они распределяются между пунктами для определения исправленных значений и вычисления координат точек. Проводится при расчетах как одиночного теодолитного хода разомкнутого и замкнутого типа с одной узловой точкой, так и целых систем.
Для чего оно выполняется?
Теодолитные ходы довольно часто прокладываются для развития планового обоснования на застроенных территориях. В свою очередь они формируют два вида систем:
- Свободные системы. Для таких ходов характерно наличие только одного твердого пункта и одной линии, чей дирекционный угол (азимут) известен. Строится в виде замкнутого полигона или их систем.
- Несвободные системы. Опираются на два твердых пункта и более. Это одиночные ходы, концы которых закреплены на жестких пунктах или узловых точках, опирающихся на них.
Различают для вида уравнивания:
- Строгое. Основано на методе наименьших квадратов и используются при обработке геодезических сетей.
- Нестрогое или упрощенное. Проводится при упрощении вычислений и применяется именно при уравнивании теодолитного хода.
В зависимости от теодолитного хода и количества узловых точек зависят дальнейшие уравнительные вычисления. Проблема уравнивания всегда была достаточно важной в геодезии, особенно при создании опорных сетей на земной поверхности и в ее недрах.
К основным его задачам относят:
– определение точных значений искомых величин и их функций по результатам проводимых измерений;
– оценка точности измерений;
– оценка точности функций измеренных данных.
Даже самое точное и многократно повторяющееся измерение одной точки невозможно без погрешностей, появление которых провоцируют множество факторов. Это могут быть как погрешности прибора, условия внешней среды, так и сам человек.
По этой причине даже при вычислении суммы углов полигона появляются невязки, которые вносят неоднозначность в данные. На практике, при уравнивании хода находят эти невязки, устраняя их или сведя к минимуму, определив наиболее вероятное значение измеренных величин.
Однако из-за уравнивания углов некоторые могут быть искажены, ведь при введении поправок в измерения некоторые величины исправятся в большую или меньшую сторону. Это компенсируется тем, что значения неправильно измеренных углов станут более точными.
Уравнивание в замкнутом теодолитном ходе
Сложные системы ходов разбиваются на два порядка увязки. Основные системы составляют первый порядок увязки и охватывают всю территорию съемки, а второго порядка – заполняют опирающиеся на них точки.
За исходные данные берутся:
– координаты и их приращения.
Расчеты отдельного полигона выполняются в специальной ведомости установленной формы. Кроме того, на каждый ход, который является частью системы обоих порядков, необходимо выделить отдельную ведомость.
Сами вычисления имеют такую последовательность:
- Вычисление практической суммы углов \(\sum \beta _<пр>\) и \(\sum \beta _<теор>\).
- Определение угловой невязки:
Далее следует вычисление дирекционных углов и азимутов:
Где \(\alpha _
\(\beta _<лев>\) –левый угол, а \(\beta _<пр>\) – правый.
\(\Delta X=s\cdot cos\cdot \alpha \)
\(\Delta Y=s\cdot sin\cdot \alpha \)
Уравнивание разомкнутой фигуры
В качестве рассмотрения возьмем ход между двумя жесткими пунктами с измеренными примычными и горизонтальными углами, а также расстояниями между ними. Производится уравнивание такого теодолитного хода следующим образом:
- Рассчитывается теоретическая сумма углов:
Правые углы:
Где \(\alpha _ <1>\) – дирекционный угол (азимут) начальной линии, а \(\alpha _
\(n\)– количество углов теодолитного хода (учитываются и примычные).
Где \(X_<1>,Y_<1>\) – координатные значения начального опорного пункта, а \(X_<2>,Y_<2>\) – конечного опорного пункта.
Определяют невязки в приращениях \(f_
\(f_
\(f_
Вычисляется абсолютная невязка \(f_\) в периметре теодолитного хода:
Другие методы уравнивания
Системы свободных теодолитных ходов часто требуют использования способов узлов или полигонов В.В. Попова. Они подразумевают составление и решение уравнений поправок при помощи красных чисел. Первый является более строгим, но разница в поправках обоих способов в уравнивании углов хода доходит до 0,3´, а в приращениях – до 0,01 м.
Если в системе минимуму из трех ходов присутствует одна узловая точка, необходимо найти дирекционный угол по формуле общей арифметической середины. Уравнивание совместной системы полигона с твердыми пунктами полигонометрии требует применения методов эквивалентной замены.
При уравнивании задача геодезиста состоит в определении значений поправок при помощи наиболее подходящего под ситуацию математического метода.
В целом, для решения задач, связанных с уравниванием теодолитного хода и других геодезических построений, прибегают к следующим разделам высшей математики:
– дифференцирование и интегрирование;
– теория матриц и линейных уравнений и т.д.
Как выполняется уравнивание сегодня
Раньше все расчеты выполнялись вручную, а в некоторых случаях с использованием специальных ЭВМ, которые по своим мощностям никак нельзя сравнить с современными компьютерами. Это имело ряд существенных недостатков, начиная с того, что все результаты хранились исключительно в бумажном виде и занимали большое количество времени.
Сегодня обработка измерений стала куда менее трудоемкой задачей. Специалисту достаточно только ввести необходимые переменные, выбрать способ обработки, внеся ряд коррективов, чтобы результат был рассчитан программой.
Однако геодезисту все равно необходимо знать все способы проведения работ, даже если они в настоящее время они не применяются на практике. В этом и состоит его ценность как квалифицированного специалиста, который может выполнить работы даже в случае возникновения непредвиденных обстоятельств, от которых не застрахованы ни на одном производстве.
Источник
Уравнивание системы нивелирных ходов с одной узловой точки
Б3.Б.5 ГЕОДЕЗИЯ
Б3.Б.2 ГЕОДЕЗИЯ
Практическое занятие.
Уравнивание системы нивелирных и теодолитных ходов
Направление: 120700 Землеустройство и кадастры
120100 Геодезия и дистанционное зондирование
Рекомендовано к изданию методической комиссией факультета землеустройства и лесного хозяйства (протокол № 1 от 03. 09. 2012 г.)
Составители: доцент Ишбулатов М.Г., ст. преп. Яковлева Ю.Н.
Рецензент: доцент, к.т.н. Лемешев А.И.
Ответственный за выпуск: заведующий кафедрой кадастра
недвижимости и геодезии, к.с-х..н., доцент Ишбулатов М.Г.,
г. Уфа, БГАУ, кафедра кадастра недвижимости и геодезии
Общие сведения
Съемочная сеть, делится на плановую и высотную.
Плановая высотная сет в зарыто местности строится в виде отдельных теодолитных ходов или систем теодолитных ходов, опирающихся на пункты исходной геодезической сети, а также в виде свободных сетей теодолитных полигонов.
Высотная геодезическая сеть строится методом геометрического или тригонометрического нивелирования. Она может состоять из отдельных нивелирных ходов или систем нивелирных ходов, опирающихся на пункты исходной высотной сети более высокого класса, а также в виде сетей свободных полигонов.
При уравновешивании несвободных съемочных сетей координаты или отметки пунктов исходной сети должны быть известны, при этом они рассматриваются как безошибочные и не подлежат исправлению. Поэтому такие пункты часто называют твердыми.
Рассмотрим уравновешивание свободных и несвободных сетей ходов. Для этих сетей существуют различные способы уравновешивания.
Уравнивание системы нивелирных ходов с одной узловой точки
Требуется уравновесить систему нивелирных ходов с одной узловой точки по рисунку 1, опирающуюся на пункты нивелирования ранее построенной сети более высокого класса, если известны: отметки исходных пунктов На, Нв, Нд, суммы измеренных превышений по ходам h1 h2, h3, длина ходов L1 L2,L3.
Рисунок 1 Схема нивелирных ходов
Составляется схема ходов, и вычисляются невязки с суммой превышений по наиболее коротким ходам. Для определения достоверности вычисляют допустимую невязку по формуле 2.1..
где Z — длина хода (км).
Определяется отметка узловой точки по каждому ходу.
Для нивелирного хода определяется вес.
Средне весовое значение отметки определяется формулой 2.2.

где
Вычисляются невязки превышений по каждому ходу.
Полученные невязки распределяются на превышения соответствующих
ходов и определяются отметки точек.
Производится оценка точностей полевых работ, определяется средняя квадратическая погрешность единицы веса по формуле 2.3.

где N — количество ходов
Средняя квадратическая погрешность определения узловой точки определяется по формуле 2.4.

3 Уравнивание теодолитных ходов с одной узловой точки
Требуется уравнять систему теодолитных ходов с одной узловой точкой, опирающихся на пункты и стороны ранее построенной сети более высокого класса (рисунок 2), если известны: координаты пункты В, Д, F и дирекционные углы сторон АВ, СД, ЕF исходной сети и измеренные значения углов и длин теодолитных ходов уравниваемой системы.
Теодолитные хода уравновешивают упрощенно: вначале уравновешивают углы, затем вычисляют приращения координат, которые уравновешивают, условно считая их независимыми. Такой способ называют способом раздельного уравнивания.
Рисунок 2 Схема теодолитных ходов
Узловая сторона 2-3. Для этой линии находим значения дирекционных углов каждого хода по формуле 3.1.
где исходной формулой будет формула 3.2
По найденным значениям α находят угловые невязки по формулам 3.3, по ходам заключенными между исходными дирекционными углами, выбираем два хода с наименьшим числом углов.
Если полученные невязки оказываются допустимыми, то определяют вес каждого направления на основании формулы 3.4
где n– количество углов, k = const.
По формуле 3.5 вычисляют средне весовое значение дирекционного угла узловой линии.
α = 

Вычисление невязок, по ходам 1, 2, 3 по формуле 3.6
Σ β теор = (для разомкнутого хода) = α нач + 180 ° ·n – α кон
f βi = α – ( αi исх + 180 ° ·n – Σ βi исх ) или f βi = α – αi
f βi = α – αi – если в формуле применялись измеренные правые по ходу углы
f βi = αi – α – если в формуле применялись измеренные левые по ходу углы
Контролем правильности вычисления дирекционного угла α и невязки fβi является формула: [ p f β] = 0
Если невязки являются допустимыми, их распределяют с противоположным знаком в соответствующие ходы (поровну на каждый угол).
Вычисляют дирекционные углы всех сторон.
Средняя квадратическая ошибка измеренного угла определяется по формуле 3.7:
m = 
Средне квадратическая ошибка единицы веса определяется формулой 3.8:
μ = 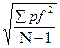
где N– число ходов.
При малом количестве числа ходов оценка точности является грубой.
По вычисленным дирекционным углам и длинам сторон вычисляют приращение координат и их суммы по ходам. Уравнивание приращений координат производится, так же как и уравнивание углов.
Для проверки правильности линейных измерений вычисляют невязки, по двум наиболее коротким ходам.
Если невязка допустима, вычисляют веса, для каждого значения координат узловой точки.
у= 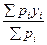
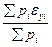

По этим координатам вычисляют невязки приращения по каждому ходу
Правильность вычисления окончательных координат узловой точки и невязку приращения координат, определяется по формуле:
[ p f x ] = 0; [ p f у ] = 0
Полученные невязки с противоположным знаком распределяются на приращения соответствующих ходов, пропорционально длинам этих ходов. После распределения невязок вычисляют координаты всех вершин теодолитных ходов.
Таблица 1 Варианты уравнивания нивелирной сети с одной узловой точкой
| Вариант | Реперы | Превышения | Расстояния | |||||
| Pn 10 | Pn ll | Pn l2 | h 1 | h 2 | h 3 | L 1 | L 2 | L 3 |
| 101,242 | 151,278 | 136,539 | 28,111 | -21,921 | -7,182 | 3,9 | 4,4 | 4,2 |
| 139,567 | 125,872 | 137,939 | -10,182 | 3,599 | -8,554 | 3,7 | 4,2 | 4,3 |
| 123,829 | 132,534 | 121,765 | 5,519 | -3,142 | 7,638 | 4,0 | 4,1 | 4,2 |
| 117,678 | 129,975 | 102,761 | -1,795 | -14,065 | 13,121 | 3,1 | 3,9 | 3,6 |
| 126,721 | 101,975 | 103,761 | -10,839 | 13,909 | 12,122 | 3,8 | 4,1 | 3,7 |
| 135,562 | 115,782 | 112,781 | -13,782 | 5,997 | 8,997 | 3,7 | 1,0 | 4,1 |
| 129,781 | 134,642 | 102,698 | -8,007 | -12,891 | 19,052 | 3,9 | 4,2 | 4,1 |
| 101,597 | 136,246 | 145,756 | 20,149 | -14,471 | -23,980 | 4,1 | 4,0 | |
| 159,761 | 161,523 | 127,693 | -17,421 | -19,182 | 14,678 | 3,8 | 4,3 | 4,2 |
| 160,843 | 131,372 | 126,593 | -18,497 | 10,971 | 15,748 | 3,6 | 3,9 | 3,5 |
| 25,92 | 27,861 | 32,676 | 4,669 | 2,721 | -2,095 | 3,2 | 4,1 | 3,6 |
| 28,21 | 31,672 | 54.925 | 2,489 | -1,062 | -4,235 | 3,5 | 4,2 | 3,3 |
| 34,26 | 32,821 | 28,563 | -4,142 | -2,239 | 2,018 | 3,8 | 4,0 | 4,1 |
| 58,263 | 62,973 | 52,821 | -1,468 | -6,198 | 3,981 | 4,0 | 3,9 | 3,9 |
| 66,627 | 59,947 | 51,088 | -3,838 | -3,145 | 5,719 | 3,7 | 4,1 | 3,3 |
| 51,623 | 46,264 | 41,889 | -5,921 | -0,581 | 3,812 | 3,4 | 3,9 | 4,1 |
| 40,005 | 43,580 | 50,989 | 5,695 | 2.115 | -5,312 | 3,6 | 3,2 | 3,8 |
| 151,621 | 124,735 | 132,534 | -11,050 | 15,830 | 8,032 | 2,8 | 3,1 | 2,7 |
| 79,777 | 65,621 | 64,328 | -7,650 | 1 6,505 | 7,810 | 3,2 | 2,9 | 3,6 |
| 98,126 | 102,435 | 105,272 | 14,340 | 10,035 | 7,200 | 2,5 | 3,0 | 3,2 |
| 103,626 | 107,534 | 112,439 | -3,630 | -7,542 | -12,450 | 3,1 | 3,2 | 3,7 |
| 83,555 | 94,121 | 80,666 | 12,340 | 1,772 | 15,226 | 3,1 | 3,5 | 2,6 |
| 41,333 | 43,222 | 50,721 | 8,560 | 6,672 | -0,837 | 3,2 | 3,7 | 3.1 |
| 54,768 | 56,852 | 59,747 | 5,680 | 3,590 | 0,697 | 4,2 | 3,8 | 2,6 |
| 99,999 | 100,500 | 87,645 | -10,005 | -10,510 | 2,350 | 3,6 | 3,7 | 3,8 |
| 74,688 | 82,539 | 76,561 | 10,320 | 2,460 | 8,448 | 3,9 | 2,1 | 3,7 |
| 80,532 | 85,679 | 73,468 | 1,460 | -3,685 | 8,530 | 3,4 | 3,3 | 2,6 |
| 120,571 | 130,232 | 122,643 | 4,436 | -5,230 | 2,366 | 3,4 | 2,8 | 3,6 |
| 40,263 | 37,563 | 48,711 | -6,036 | 15,123 | 2,418 | 3,2 | 4,1 | 2,9 |
| 70,325 | 62,888 | 60,222 | 4,470 | 2.972 | +5,628 | 5,1 | 4,2 | 4,3 |
| 81,232 | 71,242 | 80,335 | -3,082 | 6,000 | -3,981 | 4,8 | 5,2 | 3,9 |
| 38,262 | 44,356 | 46,555 | -4,637 | -2,428 | 3,666 | 3,8 | 2,6 | 2,5 |
| 41,444 | 49,566 | 40,838 | 3,956 | -4,780 | 3,336 | 6,4 | 5,2 | 4.3 |
1. Маслов А.В. и др. Геодезия. – М.: Недра, 1980. – 528 с.
2. Баканова В.В. и др. Практикум по геодезии. – М.: Недра, 1983.– 240 с.
3. Шестюков А.Д., Баканова А.И. Справочное пособие по геодезическим работам при возведении гидротехнических сооружений. М.: Недра,
Источник












