Способ сравнения площади фигур

Площадь фигуры

В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.

Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией

Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.

Например, площадь в городе — это чаще всего красивое место с клумбами, фонтаном и памятниками.

Посевная площадь — это участок земли, предназначенный для сельскохозяйственных целей.

Сравнение площадей фигур

При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.

Например, сравним площади двух фигур: треугольника и круга.

Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.

Сравнение площадей способом наложения

Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:

Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.

Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.

Сравнение площадей заданной меркой

Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:

В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.

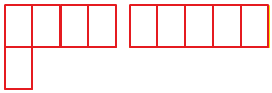
Например, меркой может быть вот такой прямоугольник :

В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.

Единицы площади

В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.

Квадратный сантиметр

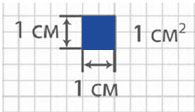
Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²

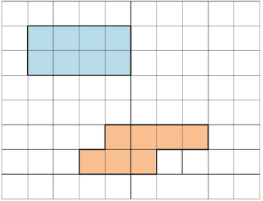
Определим площадь данных фигур:

В синей фигуре 8 см², а в красной фигуре – 7 см².

8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.

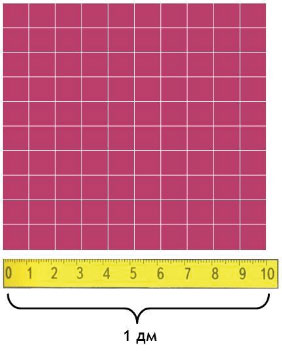
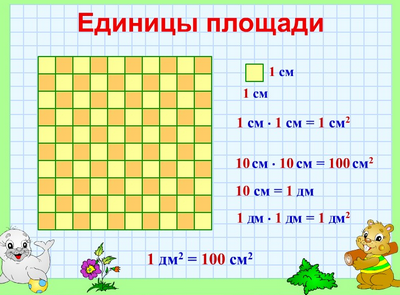
Квадратный дециметр

Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²

Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:

Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть

Значит, 1 дм² = 100 см²

Квадратный метр

Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²

Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.

1 м² = 100 дм²

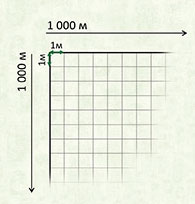
Квадратный километр

Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²

Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.

1 км² = 1000000 м²

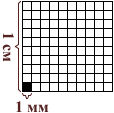
Квадратный миллиметр

Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²

Этой единицей мы пользуемся для измерения очень маленьких площадей.

1 см² = 100 мм²

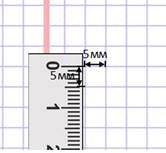
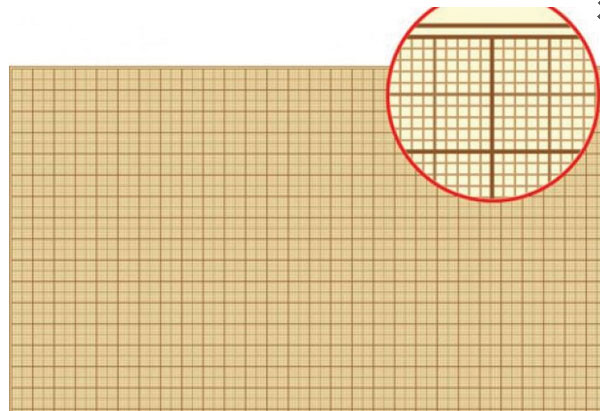
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.

Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.

Ар

Ар — это площадь квадрата со стороной 10 м.

Слово «ар» при числах сокращённо записывают так:

1 а 2 = 100 м 2 , поэтому ар часто называют соткой.

Гектар

Гектар — это площадь квадрата со стороной 100 м.

Слово «гектар» при числах сокращённо записывают так:

1 га, 20 га, 530 га.

Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.

Ар и гектар используются при измерении земельных участков.

Поделись с друзьями в социальных сетях:

Источник

Математика. 3 класс

Конспект урока

Математика, 3 класс

Урок №21. Площадь. Способы сравнения фигур по площади. Единица площади – квадратный сантиметр

Перечень вопросов, рассматриваемых в теме:

— что такое площадь фигуры?

— какие есть способы сравнения фигур по площади?

— что такое квадратный сантиметр?

Глоссарий по теме:

Площадь – внутренняя часть любой плоской геометрической фигуры.

Квадрат – это прямоугольник, у которого все стороны равны.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 56-59.

2. Рудницкая В. Н. Тесты по математике:3 класс. М.:Издательство «Экзамен», 2016 с. 38-43.

3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС. М.: Издательство «Экзамен», 2018, с. 36-53.

Теоретический материал для самостоятельного изучения

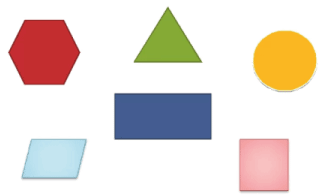
Сравним фигуры и расставим их в порядке убывания их площади.

Фигуры расположили в следующем порядке: 4, 2, 1, 6, 5, 3.

В математике говорят: площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией. Когда мы сравниваем площади фигур, мы выясняем, больше или меньше места занимает данная фигура на плоскости. Мы сравнивали эти фигуры способом, который называется «на глаз».

Сравним фигуры и выясним, площадь какой фигуры больше.

Способом сравнения на глаз, определить площадь какой фигуры невозможно.

Для этого существует способ сравнения: наложения.

Вывод: площадь прямоугольника больше площади круга.

Сравним две фигуры.

Изученными способами сравнить площади не получается. Есть еще один способ сравнения: подсчет количества одинаковых мерок.

Посчитаем количество мерок в фигурах: в синей фигуре содержится 6 мерок, в красной-5 мерок, следовательно, площадь синей фигуры больше площади красной, т. к. в синей фигуре 6 мерок-квадратов, а в красной — 5.

В математике мерка- квадрат. А квадрат со стороной 1 см называется квадратный сантиметр и обозначается см 2. .

Задания тренировочного модуля:

1.Выберите правильное высказывание:

Площадь фигуры — это…..

1. сумма длин всех сторон

2. внутренняя часть фигуры

2. внутренняя часть фигуры

2. Выделите фигуры с одинаковой площадью.

Источник

Разработка конспекта урока по математике на тему «Площадь. Способы сравнения фигур по площади.» (3 класс)

Муниципальное общеобразовательное учреждение

«Школа № 106 города Донецка»

Учитель Алексеенко Виктория Петровна

Тема: Площадь. Способы сравнения фигур по площади.

Цели: познакомить с различными способами сравнения площади разных фигур : «на глаз», путём наложения одной фигуры на другую, путём подсчета клеток одинаковой величины ; совершенствовать вычислительные навыки и умение решать текстовые задачи; развивать внимание и логическое мышление; воспитывать сотрудничество.

Планируемые результаты: учащиеся будут понимать значение понятия «площадь»; научатся самостоятельно сравнивать разными способами площади фигур; в дальнейшем будут применять теоретические знания на практике.

Оборудование: большие геометрические фигуры (треугольник, квадрат, круг, прямоугольник, овал, пятиугольник); раздаточный материал: 17 красных кругов, 17 синих кругов, 17 зелёных квадратов, 17 белых прямоугольников, 17 белых квадратов, 17 красных прямоугольников; 4 конверта с заданиями для групп, музыкальный центр, проектор, экран.

Учебник: Математика. 3 класс. Учебник для общеобразовательных организаций. В 2 частях. Часть 1 / [М. И. Моро, М. А. Бантова,

Г. В. Бельтюкова и др.]. – 6-е издание. – М.: Просвещение, 2016. – 112с.: ил. – (Школа России).

І . Организационный момент.

Проверяй скорей, дружок:

Ты готов начать урок?

Все ль на месте,

Всё ль в порядке:

Ручка, книжка и тетрадка?

Все ли правильно сидят?

Все ль внимательно глядят?

Каждый хочет получать

Только лишь оценку «пять». (Слайд 2)

ІІ . Актуализация знаний.

а) На столе 4 яблока. Одно из них разрезали пополам. Сколько яблок на столе? (4)

б) Кролики прыгали: 1-й между 2-ым и 3-им в ряд; 1 впереди, а 2 позади; 1 позади, а 2 впереди. Сколько было кроликов? (3)

в) Ряд начинается с числа 4, а каждое следующее число в нем на 1 больше предыдущего. Назовите пятое число в этом ряду. (8)

— Увеличь в 7 раз 8, 3, 5, 7.

— Уменьши в 6 раз 42, 36, 6, 54.

— Увеличь на 7 числа 14, 63, 21, 35.

— Уменьши на 6 числа 30, 42, 24, 18. (Слайд 3)

3. Создание проблемной ситуации.

— Ребята, какие геометрические фигуры вы знаете? (Круг, овал, треугольник, квадрат, четырехугольник, многоугольник, прямоугольник) (Слайд 4)

— Чем фигуры отличаются одна от другой? (Формой, размером, количеством углов или их отсутствием, цветом)

— Назовите свойства данных фигур.

— Какая из них больше всего занимает места? (Квадрат)

— Как определили? (Видно «на глаз», что квадрат больше, чем другие фигуры.

Значит, он места займёт больше)

Беру квадрат, прикладываю к доске, обвожу его мелом по контуру и убираю фигуру.

— Что видите? (Квадрат на доске занимает определенное место)

— Предположите: как называется место, которое занимает фигура? (Ответы детей)

— Обратимся к словарю Ожегова. Это понятие объясняется так: «Величина, которая указывает на то, сколько места занимает фигура на плоскости – называется площадью». (Слайд 5)

Заучивание определения наизусть.

— Повторим новое математическое понятие. (Слайд 6)

— Прочитайте ещё раз это слово на экране. Назовите изученные орфограммы.

Вывод: Каждая фигура занимает в пространстве определенное место и имеет площадь.

ІІІ . Определение темы урока, постановка учебной задачи.

— Предположите, какая у нас сегодня тема урока? (Площадь.)

После ответов учащихся появляется (Слайд 7) «Тема: «Площадь. Способы сравнения фигур по площади»

— Как вы думаете, чему мы будем сегодня учиться? (Учиться сравнивать и определять: площадь какой фигуры больше или меньше)

— Сегодня на уроке вы будете исследователями и самостоятельно узнаете, как можно сравнивать площади фигур.

IV . Работа над новым материалом.

1. Работа в парах (с раздаточным геометрическим материалом).

— Какие геометрические фигуры лежат у вас на столе? (Круги, квадраты, прямоугольник). (Слайд 8)

Задание 1 . Что можете сказать о площади прямоугольника по сравнению с площадью других фигур? (Прямоугольник больше по размеру, следовательно, его площадь больше площади других фигур).

— Каким способом определили? (Определили «на глаз»)

— Назовите предметы в классе, которые имеют площадь. (Доска, картина, стенд, парта и т.д.)

— Площадь какого предмета больше? (Площадь доски)

— Каким способом пользовались? («На глаз»)

Задание 2. Возьмите красный круг и зелёный квадрат. (Слайд 9)

Можно ли «на глаз» сравнить их площади? (Нет)

— Почему? (Это сделать трудно. Одна фигура с углами, у второй углы отсутствуют)

— Найдите другой способ сравнения. (Наложить одну фигуру на другую)

— Какой вывод можно сделать?

Вывод: Так как круг полностью поместился в квадрат, площадь квадрата больше площади круга, а соответственно площадь круга меньше площади квадрата.

Задание 3. Возьмите 2 круга (красный и синий). (Слайд 11) Сравните их площади. Что заметили? (Площади одинаковые) Каким способом пользовались? (Можно наложением или «на глаз»)

Вывод: при наложении фигуры полностью совпали, значит их площади равны.

Задание 4. Сравните площади тетради и учебника. Что можете сказать об их

площадях? (Площадь учебника больше площади тетради, соответственно площадь тетради меньше) (Слайд 12)

Задание 5. Возьмите белые квадрат и прямоугольник. Сравните. Можно ли «на глаз» сравнить их площади? (Нет) Почему? (Трудно это сделать)

А наложением? (Нет) Почему? (Ответы детей)

Проблема: как сравнить площади фигур, если «на глаз» и наложением одной на другую не получается?

— Чтобы ответить на этот вопрос, переверните фигуры. Что вы видите? (Фигуры поделены на клетки) (Слайд 13)

— Что можете сказать о размерах клеток? (Они одинаковые)

— Что можно сделать? (Посчитать количество клеток в каждой фигуре. Сравнить)

Вывод: в квадрате 9 клеток, а в прямоугольнике – 8. 9>8. Значит, площадь квадрата больше площади прямоугольника.

V . Физкультминутка. (Слайд 14)

Мы похлопаем в ладоши

Наши ножки постучали

По коленочкам ударим

Наши ручки, поднимайтесь

Наши ручки закружились,

VI . Закрепление нового материала.

Работа в группах

— Повторим правила работы в группе

* Работают все члены … (группы)

* Говорим в полголоса, чтобы… (не мешать другим)

* Внимательно слушаем друг друга, не… (перебиваем)

* Один ученик защищает работу группы, говорит… (громко и четко)

Задания выдаю в конвертах.

1 группа. Каждый из 2 прямоугольников состоит из 4-х квадратов разной

«Сравните площади фигур и сделайте вывод».

(Сосчитав количество квадратов в каждой фигуре, учащиеся могут прийти к ложному выводу, что площади данных фигур равны, так как число квадратов оказывается одинаковым. Возможно, дети сразу придут к верному решению).

— В чём дело? Может, вы ошиблись в подсчётах квадратов? (Та и другая фигура состоят из четырёх квадратов. Но квадраты разной величины. Видно «на глаз», что фигура 1 больше фигуры 2).

Вывод: при сравнении площадей фигур необходимо пользоваться одной и той же единицей измерения площади.

— О необходимости измерять площадь одной единицей измерения мы поговорим завтра.

2 группа. 2 различные фигуры изображены на клетчатой бумаге.

Задание. «Сравните площади фигур А и В. Докажите правильность полученного результата».

(А>B, т.к. фигура А составлена из 10 клеток, а фигура В — из 8; 10>8).

3 группа. Работа по учебнику с.57. Задача на смекалку.

Задание. «Как легче узнать, площадь какой фигуры больше?»

(Сосчитать клетки. Площадь собаки больше, т.к. она из 48 клеток, а заяц из 42).

Задание. «На рисунке изображены фигуры, которые при наложении не совпадут. Докажите, что их площади равны».

(Площади равны, т.к. каждая фигура состоит из 4 квадратов (клеток)).

VII . Обобщение и систематизация выученного ранее материала.

Решение примеров с.57 № 2 (дети выходят к доске по одному цепочкой и выполняют задание)

Решение задачи с.57 № 4 (коллективно)

Решение уравнений с.57 № 5 (1-е уравнение – 1 вариант; 2-е уравнение – 2 вариант)

VIII . Подведение итогов. Рефлексия.

— Наш урок подходит к завершению, давайте подведем итог.

— Назовите тему урока.

— Что называют площадью фигуры?

— Какими способами мы можем сравнить площади фигур?

— Каким по сложности вам показался урок?

— Оцените свою работу на уроке. (Слайд 16) Выберите тот смайлик, который отвечает вашему настроению, характеризует вашу работу на уроке и нарисуйте его в тетради. (Слайд 17)

Домашнее задание: с.57 № 3; № 5 (3-е и 4-е уравнения).

Источник