- Математика открытый урок по теме: «Закрепление изученного. Сравнение длин отрезков план-конспект урока по математике (1 класс) на тему
- Скачать:
- Предварительный просмотр:
- Подписи к слайдам:
- Предварительный просмотр:
- Сравнение отрезков
- Метод наложения:
- Измерение длин:
- Как сравнить длины отрезков?
- Метод наложения
- Измерение длин:
- Как сравнить 2 отрезка: способы решения задачи
- Что такое отрезок
- Сравнение двух отрезков
- Вывод
- Прямая и отрезок, измерение и сравнение отрезков
- Отрезок
- Сравнение отрезков
- Как сравнить длины отрезков: наложение и измерение, объяснение и примеры
- Способы сравнения двух отрезков
- Измерение длины
- Наложение друг на друга
Математика открытый урок по теме: «Закрепление изученного. Сравнение длин отрезков
план-конспект урока по математике (1 класс) на тему
Конспект открытого урока. Презентация
Скачать:
| Вложение | Размер |
|---|---|
| Презентация по теме урока | 1.52 МБ |
| Конспект открытого урока | 21 КБ |
Предварительный просмотр:
Подписи к слайдам:
На день Рождения к лисе медведь пришел позже, ч ем заяц, а волк- раньше, чем заяц. Кто пришёл на день рождения к лисе первым?
Предварительный просмотр:
по математике в 1 классе
по теме: «Закрепление изученного.
Сравнение длин отрезков.
учитель 1 «Б» класса
Цели: Познакомить со способами сравнения отрезков., закреплять навыки прибавления и вычитания числа., с помощью разложения числа.
Планируемые результаты: учащиеся научаться сравнивать отрезки, измерять отрезки новыми способами, анализировать и решать текстовые задачи (ИКТ), закрепление прибавления и вычитания числа 3, работать в парах и оценивать товарища, оценивать свои достижения, границы своего знания и незнания.
Приготовили рабочее место, учебник и тетради положили на край стола, пенал посередине. Проверили свою посадку за столом.
- Актуализация знаний.
- Заполняем домики (состав числа на 7,8,9,10.).Работа в парах.
- Презентация ИКТ- решение задачи на внимание.
На день рождения к лисе медведь пришёл позже, чем заяц, а волк- раньше, чем заяц. Кто пришёл на день рождения к лисе первым? (Волк).
- Устный счет.
- Увеличь 4 на 3,
- Уменьши 9 на 0
- Найди сумму чисел 5 и 4
- Найди сумму чисел 4 и 4
- Чему равно второе слагаемое, если первое равно 3. А сумма 9?
- Самоопределение к деятельности. (Заранее учитель раздает детям нитки разной длины)
Внимание! Посмотрим на экран.
Жил у бабушки- котенок, он был шалун, увидел он у нее мотки с нитками, подхватил он клубок и давай его гонять. Перепутал бабушке все нитки. Ох и разозлилась бабушка на котенка! А делать нечего, все равно придется нитки разбирать. Что-то распутала, а что пришлось и отрезать. Посмотрите, какие части получились. Скажите пожалуйста, все ли нитки мы можем на глаз сравнить друг с другом? (Нет, а почему?) Они не ровные .
Самые ровные я подобрала вам и предлагаю их померить на глаз, сравнить между собой, и измерить с помощью линейки. Вот цель нашего сегодняшнего урока.
(На партах у учащихся по два отрезка: красный- 5 см и синий 8 см.)
-Какой отрезок длиннее? — синий.
-Почему так решили? – (это видно на глаз.)
-Как проверить, не ошиблись ли мы? — (измерить длины отрезков). Какой отрезок длине на сколько см? – (синий отрезок на 3 см дине, т.к 8 см- 5 см= 3 см.)
-Каким способом можно еще сравнить длины отрезков? – (наложением).
— Как правильно наложить отрезки? – (совместить начало отрезков)
-Какой отрезок длиннее и на сколько? – (синий, на незакрытую часть.)
-Какой отрезок короче? – ( красный короче на отогнутую часть).
-Как думаете, чему равна длина отогнутого отрезка?
— Давайте измерим ее длину! (3 см)
Встали мы с рабочих мест
Руки в стороны разведем
И на поясе сомкнем
Грозно топнем правой ножкой
Левой, шаркнем не спеша
И за стол тихонько — скок
И продолжим наш урок.
- Закрепление изученного материала. Работа в тетради.
Открывайте учебник на стр.108, задание №2. Откройте тетради, запишите число.(Сегодня 8 декабря).Четыре клетки вниз от предыдущего задания на пятой строчке пишем число. Давайте измерим отрезки в книге, чему они равны, и начертим их в тетради. Как вы думаете в книге какой способ показан? — (на глаз).
Мы начертим отрезки , чтобы померить линейкой и сравнить.
— Чему равен розовый отрезок (10 см)
-Чему равен голубой отрезок (9 см)
Который из них длиннее и на сколько? (Розовый и на 1 см). Отложили тетради, поработаем устно.
Составляем задачу со знаком + ( с места ответ ученика)
Составляем задачу со знаком – (с места ответ ученика).
Чему мы сегодня научились на уроке. Кто научился измерять и сравнивать отрезки?
Оцените свои достижения с помощью светофора.
— Какие способы сравнения отрезков вы узнали? На этом наш урок окончен.
Источник
Сравнение отрезков
Одной из простейших геометрических фигур является отрезок. Для того чтобы сравнивать отрезки, можно использовать два способа:
Метод наложения:
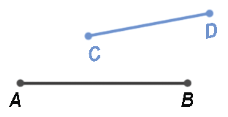
Пусть нам даны два отрезка AB и СD:
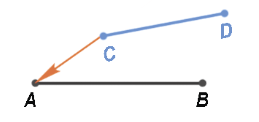
Совместим начало отрезка AB и СD (точки A и С).
Затем повернем отрезок СD так, чтобы он совпал с отрезком AB.
Мы видим, что отрезок СD составляет часть отрезка AB, следовательно, мы можем сделать вывод, что отрезок AB больше отрезка СD.
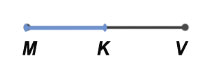
Если точка делит отрезок на равные отрезки, то эту точку называют серединой отрезка.
MK = KV, K — середина отрезка.
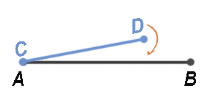
Рассмотрим еще одну пару отрезков HG и ST.
Совместим начало отрезка HG и ST.
Затем повернем отрезок ST так, чтобы он совпал с отрезком HG.
В данном случае мы видим, что совпали не только точки S и H (начала отрезков HG и ST), но и точки G и T (концы отрезков HG и ST), то есть отрезки совпадают, а нам известно, что две геометрические фигуры называются равными, если их можно совместить наложением.
Вывод:
Измерение длин:
Для измерения отрезков, необходимо наложить на него единичные отрезки, и длиннее будет считаться тот отрезок, которому соответствует большее число единичных отрезков.
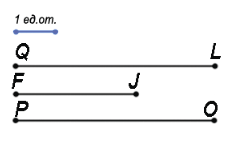
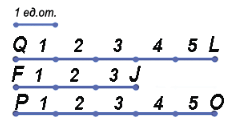
Пример: Пусть у нас есть единичный отрезок. Рассмотрим три отрезка QL, FJ и PO.
Наложим единичный отрезок на данные.
Посчитаем, какое количество единичных отрезков накладывается на каждый из отрезков, получаем: QL = 5 ед.от., FJ = 3 ед.от., PO = 5 ед. от.
Сравним отрезки: QL > FJ (т.к. 5 > 3), FJ
- Если при наложении отрезков оба их концасовмещаются, значит отрезкиравны.
- Если при измерении отрезков их длиныравны, то отрезки равны.
Поделись с друзьями в социальных сетях:
Источник
Как сравнить длины отрезков?
Сравнить 2 отрезка на плоскости — это типичная задача по геометрии для учеников 7 класса. Существует несколько разных методов выполнения данного сравнения, и мы подробно расскажем о каждом из них.
Подобного рода задачи выполняются элементарно и являются основой для изучения дальнейшего материала. Стоит один раз запомнить этот несложный процесс, и в дальнейшем уже не возникнет никаких трудностей с аналогичными заданиями.
Метод наложения
Одной из простейших геометрических фигур является отрезок . Для того чтобы сравнивать отрезки, можно использовать два способа:
Пусть нам даны два отрезка AB и СD:
Совместим начало отрезка AB и СD (точки A и С).
Затем повернем отрезок СD так, чтобы он совпал с отрезком AB.
Мы видим, что отрезок СD составляет часть отрезка AB, следовательно, мы можем сделать вывод, что отрезок AB больше отрезка СD.
Если точка делит отрезок на равные отрезки, то эту точку называют серединой отрезка.
MK = KV, K — середина отрезка.
Рассмотрим еще одну пару отрезков HG и ST.
Совместим начало отрезка HG и ST.
Затем повернем отрезок STтак, чтобы он совпал с отрезком HG.
В данном случае мы видим, что совпали не только точки S и H (начала отрезков HG и ST), но и точки G и T (концы отрезков HG и ST), то есть отрезки совпадают, а нам известно, что две геометрические фигуры называются равными, если их можно совместить наложением.
Вывод:
Измерение длин:
Для измерения отрезков, необходимо наложить на него единичные отрезки, и длиннее будет считаться тот отрезок, которому соответствует большее число единичных отрезков.
Пример: Пусть у нас есть единичный отрезок. Рассмотрим три отрезка QL, FJ и PO.
Наложим единичный отрезок на данные.
Посчитаем, какое количество единичных отрезков накладывается на каждый из отрезков, получаем: QL = 5 ед.от., FJ = 3 ед.от., PO = 5 ед. от.
Сравним отрезки: QL > FJ (т.к. 5 > 3), FJ https://budu5.com/manual/chapter/3301
Как сравнить 2 отрезка: способы решения задачи
Что такое отрезок
Прежде чем рассказать, как сравнить 2 отрезка, давайте разберем, что такое отрезок на плоскости.
Определение из учебника по геометрии гласит, что отрезок — это часть прямой, которая с двух сторон ограничивается двумя точками.
Если рассматривать одну прямую, отрезком будет считаться множество, которое состоит из двух разных точек этой прямой (собственно, концов отрезка), а также остального множества из всех точек, которые располагаются между ними (так называемых внутренних точек).
Сравнение двух отрезков
Итак, в вопросе о том, как сравнить 2 отрезка, можно выделить следующие методы:
- Наложение. Для того чтобы выполнить сравнение двух отрезков, нужно выполнить наложение одного из них на другой. Соответственно, тот отрезок, который будет содержать внутри себя второй отрезок целиком, больше. Если концы этих отрезков совпали — значит, их длины равны.
- Второй способ, как сравнить 2 отрезка в геометрии — это выяснить, на какое количество единиц отличается их длина. Для этого нужно при помощи линейки с одинаковыми значениями провести измерение сначала одного отрезка, затем другого, и из первого результата вычесть второй.
В том случае, если разность составит положительное число, значит, первый отрезок длиннее второго на соответствующее количество единиц. Если в результате получено нулевое значение — отрезки равны. А если в ответе отрицательное число, следовательно, второй отрезок длиннее первого.
Вывод
Итак, мы выяснили, как сравнить 2 отрезка. Первый способ указывает только на то, какой из них будет длиннее, а какой — короче, а второй показывает числовое значение разницы в длине.
Прямая и отрезок, измерение и сравнение отрезков
Понятие прямой, также как и понятие точки является основными понятиями геометрии. Как известно основные понятия не определяется. Это не является и исключением для понятия прямой. Поэтому рассмотрим суть этого понятия через его построение.
Возьмем линейку и, не отрывая карандаша, проведем линию произвольной длины.
Полученную линию мы и будем называть прямой. Однако тут необходимо отметить, что это не вся прямая, а только её часть. Всю же прямую построить не имеется возможным, она является бесконечной на обоих своих концах.
Прямые будем обозначать маленькой латинской буквой, либо двумя её точками в круглых скобках.
Понятия прямой и точки связаны тремя аксиомами геометрии:
- Аксиома 1: Для каждой произвольной прямой существует как минимум две точки, которые на ней лежат.
- Аксиома 2: Можно найти как минимум три точки, которые не будут лежать на одной и той же прямой.
- Аксиома 3: Через $2$ произвольные точки всегда проходит прямая, причем эта прямая единственна.
Для двух прямых актуально их взаимное расположение. Возможны три случая:
- Две прямые совпадают. В этом случае каждая точка одной будет также и точкой другой прямой.
- Две прямые пересекаются. В этом случае только какая-то одна точка из одной прямой будет также принадлежать и другой прямой.
- Две прямые параллельны. В этом случае у каждой из этих прямых свой набор различных друг от друга точек.
В этой статье мы не будем подробно останавливаться на этих понятиях.
Отрезок
Пусть нам дана произвольная прямая и две точки, принадлежащие ей. Тогда отрезком будет называться часть прямой, которая ограничена двумя ее произвольными различными точками. Точки, которыми ограничен отрезок в рамках определения 1 называются концами этого отрезка.
Отрезки будем обозначать двумя её точками концов в квадратных скобках.
Сравнение отрезков
Рассмотрим два произвольных отрезка. Очевидно, что они могут быть либо равными, либо неравными. Чтобы разобраться в этом, нам нужна следующая аксиома геометрии.
Аксиома 4: Если оба конца двух различных отрезков совпадут при их наложении, то такие отрезки будут равными.
Итак, для сравнения выбранных нами отрезков (обозначим их отрезок 1 и отрезок 2) наложим конец отрезка 1 на конец отрезка 2, так, чтобы, отрезки оставались по одну сторону от этих концов. После такого наложения возможны два следующих случая:
- Вторые концы этих отрезков также совпадут. В таком случае по аксиоме 5 мы получим, что такие отрезки будут равны друг другу.
- Вторые корцы не совпадут. Здесь, без ограничения общности, будем считать, что конец отрезка 1 будет принадлежать отрезку 2. Тогда здесь мы говорим, что данные отрезки не равны, причем отрезок 1 короче отрезка 2.
Как сравнить длины отрезков: наложение и измерение, объяснение и примеры
Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.
Способы сравнения двух отрезков
В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.
Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.
Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (>; АБ.
Это интересно: как разложить на множители квадратный трехчлен?
Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:
- визуальный способ;
- измерительный;
- сравнение наложением;
- сравнение в координатной сетке.
Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.
Измерение длины
Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.
Наложение друг на друга
Как происходит совмещение АБ и ВГ:
- Нужно конец, А одного из них совместить с концом В другого, если совпадают и другие концы этих отрезков — Б и Г, значит, они равны, что записывается с помощью знака равно.
- Если нет, значит, один из них длиннее другого, и записывается это также с помощью математических знаков больше или меньше (> или √ 73, значит, Da > Db.
- Также можно сравнить отрезки, находящиеся в трехмерной системе координат, надо учитывать не две, а три координаты каждого из них.
Источник