Способ создания кворумных ключей схема шамира

Что такое Shamir Backup, новейший стандарт безопасности?

Биткоин предполагает высокий уровень независимости и автономности: своими ключами и монетами вы владеете и распоряжаетесь по собственному усмотрению. Но что произойдет, если вы потеряете ключи, которые защищены всего лишь одной seed-фразой?

Как незаметно хранить и защищать seed-фразы от всех возможных рисков, которые могут поджидать вас на жизненном пути?

Для безопасного хранения seed-фраз необходимо свести к минимуму любые факторы риска, что иногда может оказаться достаточно сложным. Создание копий вашей seed-фразы снижает риск потери или уничтожения, но одновременно увеличивает вероятность того, что вашу кодовую фразу могут выкрасть.

Потеря, уничтожение и кража являются самыми серьезными факторами риска при использовании seed-фраз, однако, наряду с ними, существует также ряд других моментов, на которые следует обратить внимание. Например, кто получит доступ к вашим средствам, если с вами что-то случится? Возможна ли такая ситуация, при которой злоумышленники могут вынудить вас сообщить свою seed-фразу?

Мы, к сожалению, не знаем таких магических заклинаний, которые могли бы целиком и полностью защитить вас от любых рисков. Но мы, как никто другой, в состоянии помочь вам надежно хранить и защищать резервные копии ваших ключей безопасности несмотря ни на какие жизненные невзгоды и испытания.

Новейший стандарт безопасности, доступный только на аппаратном кошельке Trezor Model T, позволяет защитить ваши ключи безопасности более надежно, чем когда-либо прежде — ShamirBackup (резервное копирование по схеме Шамира).

Мы в SatoshiLabs гордимся тем, что являемся создателями как первого аппаратного кошелька, так и всей сопутствующей отрасли. Сегодня настало время еще более раздвинуть границы и сделать очередной шаг в будущее. Мы с гордостью сообщаем, что TrezorModel T является первым и единственным в мире аппаратным кошельком, в котором реализован полностью функциональный стандарт безопасности SLIP-0039: ShamirBackup илирезервное копирование по схеме Шамира.

В основу Shamir Backup положен криптографический алгоритм, созданный Ади Шамиром и широко известный как схема разделения секрета Шамира. Резервное копирование по схеме Шамира произвело революцию в использовании, хранении и защите копий ваших личных ключей. При создании нового кошелька с помощью резервного копирования по схеме Шамира Model T, вместо создания одной seed-фразы, генерирует доли, количество которых задано пользователем и длина каждой из которых составляет 20 слов. Затем пользователь устанавливает порог (количество долей, необходимое для восстановления кошелька). Вы можете генерировать до 16 долей, но мы рекомендуем использовать простую и при этом достаточно безопасную схему (2; 3) или (3; 5) в качестве идеального порога для восстановления кошелька. Например, можно создать 6 долей и установить порог на уровне 4 долей. Это означает, что для восстановления кошелька вам нужно будет ввести любые 4 доли. Более того, даже не нужно вводить все 4 доли одновременно: вы можете отключить устройство и через время продолжить восстановление. Далее вы сами решаете, как будете хранить доли. Вы можете спрятать их, поделиться ими с людьми, которым доверяете, или же предпринять одновременно и то, и другое.

SatoshiLabs продолжает работать над усовершенствованием принципов и технологий безопасности, создавая новые отраслевые стандарты, такие как ShamirBackup, благодаря которым вы можете найти самое лучшее решение, удовлетворяющее всем вашим требованиям. Мы всегда сообщаем открытые исходные коды и приглашаем другие компании, работающие в сфере безопасности, присоединиться к нашей революции. Мы считаем, что стандарт ShamirBackup получит признание во всей отрасли и еще больше повысит стандарты безопасности аппаратных кошельков.

Если вы хотите узнать больше о резервном копировании по схеме Шамира, предлагаем ознакомиться с нашим постом в Dev Corner под названием A Detailed Guide to Shamir Backup (Подробное руководство по резервному копированию с применением криптографической схемы Шамира).

Источник

Защита приватных ключей: Схема Мультисиг против схемы Разделения Cекрета Шамира

Криптовалюты работают по основному криптографическому принципу (связке публичного и приватного ключей), что позволяет получать и отправлять транзакции. Публичные ключи подобны имени пользователя электронного почтового ящика, доступного всем желающим для просмотра и отправки криптовалюты. Приватные ключи, в свою очередь, известны только пользователю (что-то вроде пароля) и помогают их обладателю авторизовать транзакцию. Проблема заключается в том, что в отличие от паролей, приватные ключи не могут быть восстановлены для получения доступа к средствам/счетам.

Недостатком безопасного хранения любой конфиденциальной информации, такой как приватные ключи, является проблема безопасности данных:

• ПОТЕРЯ ДАННЫХ: потеря доступа к необходимым данным.
• КРАЖА ДАННЫХ: возможность доступа к конфиденциальным данным для третьих лиц.

Давайте предположим, что вы должны охранять что-то ценное, например, рецепт колы. У вас с собой только одна копия. Вы можете защитить рецепт любым из следующих способов, указанных ниже:

1. Защитить рецепт с помощью шифрования. Данный метод кажется очевидным для защиты рецепта, но, на самом деле, он просто смещает вектор атаки с нахождения рецепта на подбор ключа шифрования.
2. Оставить рецепт на хранение в банковском хранилище. Данный подход по своей сути основан на том, что банковские хранилища воспринимаются как очень безопасные. Но что произойдет в случае, если хранилище будет уничтожено по какой-либо причине, например, в результате стихийного бедствия? Вы теряете рецепт, и это становится проблемой, так как у вас в наличии имеется лишь один экземпляр данного рецепта. Что происходит в случае, если кто-то вломится в хранилище и опустошит каждый шкафчик? В подобном случае, вы не только теряете единственную копию рецепта, но его приобретает и кто-то другой, кто получает возможность извлечь из этого свою собственную выгоду. Помимо этого, восстановить рецепт по памяти не представляется возможным в силу его сложности. Очевидно, что данный подход не решает ни проблему потери данных, ни проблему их кражи.
3. Сделать несколько копий рецепта и хранить их в разных хранилищах по всему миру. Теперь, в случае, если какое-либо из хранилищ будет взломано, у вас все еще есть рецепт, и, следовательно, риск потери рецепта снижается благодаря устранению единственной точки уязвимости (single point of failure). Хотя вы по-прежнему имеете доступ к оригинальному рецепту, точная копия этого рецепта попадает к третьему лицу, которое может им воспользоваться без вашего согласия, что в данном случае является основным недостатком. Следовательно, подобный способ не решает проблему кражи данных.
4. Разбить сложный рецепт на несколько частей и хранить их в разных местах. Теперь, если что-то случится с одним из хранилищ, вы потеряете только часть рецепта, но будете иметь доступ к остальным данным. Недостатком такого подхода является то, что рецепт бесполезен по частям и имеет ценность только при условии наличия всех частей. Это приведет к сложности восстановления недостающей части и, в конечном счете, рецепта в целом. Таким образом, данный способ не решает проблему потери данных.

Подобным образом обстоит ситуация с приватными ключами, имеющими единственную точку уязвимости в блокчейне. Для более детального объяснения рекомендуем просмотреть блог, где мы сравниваем централизованную архитектуру с децентрализованной.

Мультисиг

С целью решения данной проблемы разработчики Биткоин-протокола внедрили мульти-подпись или, как это принято называть, мультисиг. Идею, стоящую за внедрением мультисига, можно понять, взяв в качестве примера банковскую ячейку. Для открытия ячейки понадобится 2 ключа: один принадлежит клиенту, а второй хранится в банке. Аналогичным образом, используя мультисиг, любой может быть уверен, что сделки могут совершаться только при условии их одобрения минимальным количеством лиц, уже обладающих ключами.

Несмотря на то, что подход, основанный на использовании нескольких ключей, является очень надежным, у него есть и свои недостатки:

• Не существует стандартной реализации схемы мультисиг для различных поддерживающих его блокчейнов. Существуют различные реализации, предложенные разными организациями, код некоторых из них даже не является открытым. Кроме того, существуют риски, связанные с изменениями on-chain протоколов, которые в идеале должны оставаться неизменными.
• При использовании несколькими участниками схемы мультисиг имеет место потеря конфиденциальности в отношении средств среди соавторов подписей. Таким образом, если третье лицо выступает в роли соавтора подписи, оно может легко отследить объемы средств. Если это третье лицо окажется злоумышленником, оно может использовать полученную информацию в собственных интересах.
• Лишь некоторые блокчейны на данный момент поддерживают схему мультисиг. Мультисиг не является универсальным решением и должно быть реализовано для каждого блокчейна отдельно, что препятствует распространению схемы. Кроме того, они не могут привычным способом быть использованы для обеспечения безопасности других цифровых активов, таких как ключи SSH.
• Сделка с несколькими центрами передачи данных сопряжена с более высокими затратами по сравнению со сделкой, совершаемой с помощью одного ключа.
• Существует ограничение на число соавторов, приемлемое для использования системы мультисиг.
• Смена схемы является нелегкой задачей. Например, если один из приватных ключей при использовании схемы “3 из 5” скомпрометирован, появляется необходимость обновить данную схему, что, в свою очередь, потребует выполнения дополнительных шагов для отправки монет на новый адрес, а именно:
• сгенерировать новый адрес мультисиг с новым приватным ключом,
• собрать как минимум 3 из 5 подписей к старому адресу

Основной альтернативой схеме мультисиг является схема разделения секрета Шамира.

Разделение секрета Шамира

Разделение секрета Шамира (РСШ) позволяет разделить секрет на определенное количество частей — n таким образом, что с помощью любых m-из-n частей можно восстановить исходный секрет. При этом, обладая лишь m-1 частями, раскрыть секрет невозможно. Это позволяет пользователю установить порог безопасности, равный количеству = ‘m’ требуемых частей. Секрет расшифровывается обладателями частей приватного ключа при достижении минимального порога с помощью Интерполяционного многочлена Лагранжа. Методика очень похожа на мультисиг, но РСШ выполняется офчейн (вне цепочки), в то время как мультисиг полностью реализован ончейн (в самой цепочке). В случае с мультисиг различные приватные ключи используются при генерации мультисиг-адреса, в то время как в РСШ один приватный ключ разбивается на несколько частей. С точки зрения баланса между удобством и безопасностью, схема РСШ предпочтительнее для физических лиц, в то время как схема мультисиг лучше подойдет предприятиям.

У схемы РСШ есть ряд преимуществ, которые ставят ее в выигрышную позицию по сравнению со схемой мультисиг:

• Поскольку вычисления производятся офчейн, можно реализовать иерархическую систему РСШ, в которой РСШ далее применяется на каждой самой части секрета. Это позволяет осуществлять многомерный контроль доступа, не представляющийся возможным при использовании мультисиг. В связи с офчейн реализацией отсутствует риск изменения протокола ончейн.
• Так как схема РСШ может быть применена к любой конфиденциальной информации, в отличие от мультисиг, стандартизированная реализация возможна для защиты любой конфиденциальной информации, такой, как приватные ключи на блокчейне, корневые ключи сервера, PGP/GPG сертификаты и т. д.
• В отличие от схемы мультисиг, РСШ может работать с любым блокчейном. Защита сид-фразы протокола BIP39 с помощью РСШ избавляет приватные ключи от проблемы единой точки отказа и позволяет защитить приватные ключи любого блокчейна.
• Конфиденциальность не теряется при условии, что совладельцы не имеют информации об открытом ключе.
• Использование одного приватного ключа приводит к снижению затрат на транзакцию.
• Количество частей, сгенерированных с помощью РСШ, практически неограничено.
• Процесс изменения схемы при использовании РСШ упрощен. Например, при использовании установки “3 из 5” РСШ, где одна из частей ключа оказалась скомпрометированной, вам просто потребуется сгенерировать новые части приватного ключа. То есть, не возникнет необходимости совершать какие-либо дополнительные операции.

В аппаратном кошельке Cypherock X1 для создания криптографических составляющих используется схема РСШ. Это гарантирует разделение фазы восстановления кошелька между различными защищенными от взлома устройствами. Результатом является обеспечение эффективности и безотказности механизма восстановления кошелька. Целью Cypherock является решение проблемы восстановления кошелька и передачи криптографических валют по наследству. Команда Cypherock заинтересована в спокойствии и абсолютной уверенности пользователей в безопасности их криптовалютных сбережений.

Заказать Cyperock X1 можно, перейдя по ссылке.

Источник

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Вспомогательная страница к разделу ИНТЕРПОЛЯЦИЯ

Разделение секрета

Помещение имело две двери, каждая с тремя замками. Ключи от этих замков находились во владении различных цехов. Документы хранились в шкафу, запиравшемся на три замка. Один ключ от шкафа хранился у фогта 1) а два других –– у главного шеффена 2) Таким образом, получить доступ к документам могли только совместно собравшиеся представители трех цехов, фогт и шеффен.

Пусть требуется «расщепить» натуральное число (ключ) $ S $ на $ n $ частей, т.е. создать новые натуральные числа (доли) $ S_1,\dots, S_n $ и распределить их среди $ n $ участников некоторого консорциума дольщиков (акционеров). Разделение должно быть организовано таким образом, чтобы для данного значения (порога 3) ) $ k 1. можно восстановить из любой подсистемы $ \< S_,\dots, S_ \> \subset \ $, содержащей $ k $ долей;

2. нельзя восстановить из меньшего числа долей.

Создание собственно ключа $ S $, а также организация вычисления его долей и распространения между дольщиками доверяются честному посреднику (дилеру). Такая схема разделения секрета называется $ (k,n) $-пороговой.

Схема Шамира разделения секрета

Среди нескольких существующих алгоритмов разделения секрета имеется следующая схема, предложенная Шамиром [1]. Она основана на решении задаче полиномиальной интерполяции. Сначала посредник выбирает достаточно большое простое число $ p> S, p \gg n $ и составляется полином степени $ k-1 $ $$ f(x):=S+a_1x+a_2x^2+\dots + a_ x^ , \quad \ \> \subset \ <0,1,\dots, p-1 \>\, . $$ Свободный член совпадает с ключом, а все остальные коэффициенты — произвольные. Далее, посредник нумерует акционеров числами $ 1,2 \dots, n $, и $ j $-му из них сообщает значение $ y_j= f(j) \pmod p $; это значение и считается $ j $-й долей секретного ключа $ S $. Для восстановления секрета $ S $, дольщики должны собрать не менее $ k $ пар $ (j, y_j) $. Далее, по формуле Лагранжа восстанавливается полином $ f(x) $ степени $ k-1 $ по модулю $ p $. Этот полином единствен и не может быть вычислен по любому набору долей, количество которых меньше $ k $. Свободный член этого полинома совпадает с $ S $. Единственной спецификой вычислений в $ \mathbb Z_p $ является та, что операцию деления, используемую в формуле Лагранжа, следует интерпретировать как операцию обращения знаменателя по модулю $ p $.

Вероятность подбора ключа случайным перебором может быть сведена к минимуму увеличением $ p $ (и техническим ограничением числа допустимых попыток его проверки).

Децентрализованный протокол голосования

Предположим, что в консорциуме из $ n $ участников нужно провести голосование — анонимное и бинарное («за» или «против»). Имеется некоторое количество $ k>2 $ администраторов — счётчиков голосов, которым каждый участник посылает свои сообщения, но, которым не доверяет результатов подсчета голосов. Как организовать подсчет результатов так, чтобы избежать их подделки?

Нумеруем голосующих и администраторов. Организуем разделение секрета. С этой целью $ \ell $ый администратор придумывает и выкладывает в открытый доступ произвольное ненулевое целое число $ x_ <\ell>$. Полученные $ k $ чисел $ x_1,\dots, x_k $ должны быть различными (если это не так, то коллизии нужно устранить).

В то же время, $ j $-й голосующий придумывает полином $ f_j(x) $ c целыми коэффициентами степени $ \le k-1 $, и с фиксированным свободным членом $ f_j(0)=+1 $ если он голосует «за» и $ f_j(0)=-1 $ если он голосует «против». Этот полином он держит в секрете.

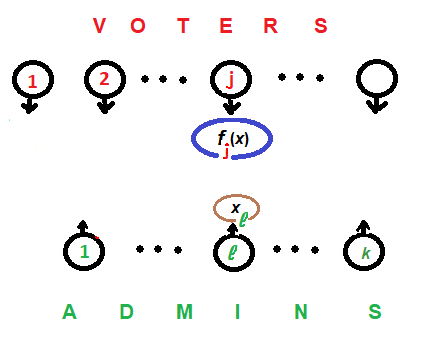
Таким образом, у участников голосования образуются система полиномов $ f_1(x),\dots, f_n(x) $ таких, что составленная из них сумма, т.е. полином $$ F(x)=\sum_^n f_j(x) $$ обладает степенью $ \deg F \le k-1 $ и свободным членом равным количеству голосов «за» минус количество голосов «против», т.е. как раз результату голосования $ S $.

Теперь осталось организовать вычисление полинома $ F(x) $ при условии, что полиномы $ \_^n $ остаются секретными.

$ j $-й голосующий вычисляет значения своего полинома при аргументах $ x_1,\dots, x_k $ и посылает получившиеся значения соответствующим администраторам: число $$ f_j(x_<\ell>) $$ отсылается от $ j $-го голосующего $ \ell $-му администратору. Фактически $ j $-й голосующий разделяет между администраторами свой секрет (результат своего голосования) по ☝ схеме Шамира.

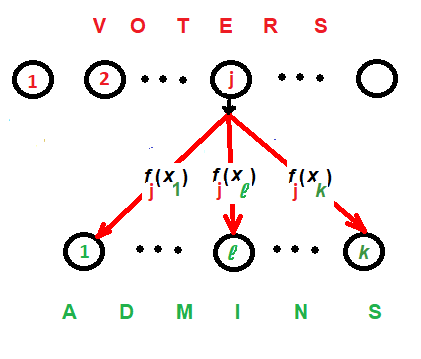
Каждый администратор суммирует полученные им значения $$ Y_<\ell>=\sum_^n f_j(x_<\ell>) $$ и выкладывает $ Y_ <\ell>$ в открытый доступ.

Очевидно $ Y_<\ell>= F(x_<\ell>) $, т.е. в открытом доступе оказываются $ k $ значений полинома $ F(x) $, степень которого не превышает $ k-1 $. Значениями $ \\>_<\ell=1>^k $ полином $ F(x) $ восстанавливается однозначно, и, следовательно, любой участник процесса голосования способен определить его результат по значению $ F(0) $.

Возможности фальсификации

$ <\color1.> $ Что препятствует подделке результата голосования $ \ell $-м администратором? — Отсутствие видимой связи полученного им числа $ f_j(x_<\ell>) $ с числом $ f_j(0) $ (результатом голосования участника). В какую сторону его подделывать, чтобы добиться нужного жулику изменения результата голосования? Тем не менее, можно предположить, что в половине случаев случайное изменение доли секрета приведет именно к желаемой для жулика коррекции.

$ <\color2.> $ Сами участники голосования предполагаются честными. Если $ j $-й из них сгенерирует полином $ \widetilde f_j(x) $ такой, что $ \widetilde f_j(0)=+3 $ и потом разошлет администраторам значения $ \widetilde f_j(x_<\ell>) $, то результатом подсчета голосов будет $ +2 $ лишних голоса «за»…

Как проконтролировать возможность подделки значений $ Y_1,Y_2,\dots $ администраторами? Заметим, что подмена истинного значения $ Y_ <\ell>$ может произойти и неумышленно, а именно, в результате искажения при пересылке какой-то доли $ y_ $. Таким образом, мы получаем задачу о восстановлении истинных значений полинома в узлах интерполяции, количество и расположение которых исходно не известно. Подобные задачи возникают в теории кодов, исправляющих ошибки. Конструктивное решение этой задачи возможно при условии, что количество истинных значений полинома $ F(x) $ значительно превосходит потенциальное количество искаженных. Более того, этих истинных значений должно быть в избытке и по отношению к количеству коэффициентов полинома, т.е. к его степени.

В схеме предыдущего пункта будем по-прежнему считать, что степень полинома $ F(x) $ не превосходит $ k-1 $. Но вот количество администраторов увеличим: пусть их теперь будет $ K>k $.

Интерполяция по избыточной таблице

Подробное изложение математических результатов настоящего пункта ☞ ЗДЕСЬ

Предположим, что задана таблица рациональных чисел $$ \begin x & x_1 & x_2 & \ldots & x_K \\ \hline y & y_1 & y_2 & \ldots & y_K \end \quad \quad \_^K \subset \mathbb Q, $$ узлы $ \_^K $ — все различны. Эта таблица однозначно определяет полином $ f(x) \in \mathbb R[x] $ такой, что $ \left\_^K $ и $ \deg f \le K-1 $. Если же оказывается, что $ k=\deg f ☞ ЗДЕСЬ. Но мы ограничимся здесь тем коэффициентом, который только и существен для нашей задачи разделения секрета.

Доказать, что при условии $ \_^K $ свободный член интерполяционного полинома можно вычислить по формуле

Предположим теперь, что некоторые из значений $ y_1,\dots, y_K $, исходно сгенерированные полиномом степени $ k 4) полиномом локаторов ошибок для избыточной, но кое-где ошибочной интерполяционной таблицы. ♦

Эмпирически обнаруженный факт обосновывается следующим общим теоретическим результатом, в котором предполагается, что число ошибочных значений $ y $ в интерполяционной таблице равно $ E $.

Теорема 2. Пусть $ E \in \ <1,2,\dots, \lfloor K/2 \rfloor-1 \>$ и $ e_1,\dots,e_E $ — различные числа из $ \ <1,2,\dots, K\>$. Пусть полином $ f(x) $ имеет степень $ k k-1 \ge \deg f_j(x) -1 $. Алгоритм обнаружения ошибок работает следующим образом.

Алгоритм обнаружения ошибок

1. Последовательно вычисляем величины $ \tau_0,\dots, \tau_ $. Если все они равны нулю, то считаем, что ошибки не обнаружены.

2. Если какое-то из этих чисел обращается в нуль, факт наличия ошибки считается установленным. Последовательно вычисляем полиномы $$ \mathcal H_ <1>(x;\<\tau\>), \mathcal H_ <2>(x;\<\tau\>), \dots $$ Для каждого полинома $ \mathcal H_ (x;\<\tau\>) $ (отличного от тождественного нуля) проверяем находятся ли его корни во множестве $ \ $.

3. Пусть $ \mathcal H_ (x;\<\tau\>) $ с $ E 4. Если ни один из полиномов $$ \mathcal H_ <1>(x;\<\tau\>),\dots, \mathcal H_ <\lfloor (K-k+1)/2 \rfloor-1>(x;\<\tau\>) $$ не обладает свойством из пункта 3 , то число ошибочных долей превосходит предположенное ограничение на их количество, и локализация этих ошибок невозможна.

Контроль корректности поведения голосующих

Теперь обратимся ко второй проблеме, поставленной в пункте ☝ ВОЗМОЖНОСТИ ФАЛЬСИФИКАЦИИ: как проверить корректность голосования каждого участника, не нарушив при этом принципа конфиденциальности?

Источники

[1]. Kersten A.G., Shared Secret Schemes aus geometrischer Sicht. Dissertation, Mitteilungen aus dem Mathematischen Seminar Gießen, Hefte 208, 1992

[2]. Gent und seine Schönheiten. Thill Verlag, Brüssel,1990

[3]. Блох М. Феодальное общество. М.Наука, 1986

[4]. Shamir A., How to share a secret, Communications of the ACM, 1979, 22 (11),pp. 612–613

Источник