Способ создания кворумных ключей схема rsa

Иллюстрация работы RSA на примере

Вокруг алгоритмов шифрования с отрытым и закрытым ключом существует множество недопониманий и мистификаций. Здесь я хотел бы предельно коротко и наглядно, с конкретными числами и минимумом формул, показать, как это работает.

Я не вдаюсь в теорию (не очень понятно, на какой уровень подготовки читателя следует рассчитывать), но я уверен, что прочитав эту короткую иллюстрацию, любому человеку будет проще разобраться в формулах и строгих доказательствах.

Итак. Допустим, я хочу получить от вас некие данные. Мы с вам не хотим, чтобы эти данные узнал кто-то, кроме нас. И у нас нет никакой уверенности в надёжности канала передачи данных. Приступим.

Шаг первый. Подготовка ключей

Я должен проделать предварительные действия: сгенерировать публичный и приватный ключ.

• Выбираю два простых числа. Пусть это будет p=3 и q=7 .
• Вычисляем модуль — произведение наших p и q : n=p×q=3×7=21 .
• Вычисляем функцию Эйлера: φ=(p-1)×(q-1)=2×6=12 .
• Выбираем число e , отвечающее следующим критериям: (i) оно должно быть простое, (ii) оно должно быть меньше φ — остаются варианты: 3, 5, 7, 11, (iii) оно должно быть взаимно простое с φ ; остаются варианты 5, 7, 11. Выберем e=5 . Это, так называемая, открытая экспонента.

Теперь пара чисел — это мой открытый ключ. Я отправляю его вам, чтобы вы зашифровали своё сообщение. Но для меня это ещё не всё. Я должен получить закрытый ключ.

Мне нужно вычислить число d , обратное е по модулю φ . То есть остаток от деления по модулю φ произведения d×e должен быть равен 1. Запишем это в обозначениях, принятых во многих языках программирования: (d×е)%φ=1 . Или (d×5)%12=1 . d может быть равно 5 ( (5×5)%12=25%12=1 ), но чтобы оно не путалось с e в дальнейшем повествовании, давайте возьмём его равным 17. Можете проверить сами, что (17×5)%12 действительно равно 1 ( 17×5-12×7=1 ). Итак d=17 . Пара — это секретный ключ, его я оставляю у себя. Его нельзя сообщать никому. Только обладатель секретного ключа может расшифровать то, что было зашифровано открытым ключом.

Шаг второй. Шифрование

Теперь пришла ваша очередь шифровать ваше сообщение. Допустим, ваше сообщение это число 19. Обозначим его P=19 . Кроме него у вас уже есть мой открытый ключ: = <5, 21>. Шифрование выполняется по следующему алгоритму:

• Возводите ваше сообщение в степень e по модулю n . То есть, вычисляете 19 в степени 5 (2476099) и берёте остаток от деления на 21. Получается 10 — это ваши закодированные данные.

Строго говоря, вам вовсе незачем вычислять огромное число «19 в степени 5». При каждом умножении достаточно вычислять не полное произведение, а только остаток от деления на 21. Но это уже детали реализации вычислений, давайте не будем в них углубляться.

Полученные данные E=10 , вы отправляете мне.

Здесь надо заметить, что сообщение P=19 не должно быть больше n=21 . иначе ничего не получится.

Шаг третий. Расшифровка

Я получил ваши данные ( E=10 ), и у меня имеется закрытый ключ = <17, 21>.

Обратите внимание на то, что открытый ключ не может расшифровать сообщение. А закрытый ключ я никому не говорил. В этом вся прелесть асимметричного шифрования.

• Я делаю операцию, очень похожую на вашу, но вместо e использую d . Возвожу E в степень d : получаю 10 в степени 17 (позвольте, я не буду писать единичку с семнадцатью нулями). Вычисляю остаток от деления на 21 и получаю 19 — ваше сообщение.

Заметьте, никто, кроме меня (даже вы!) не может расшифровать ваше сообщение ( E=10 ), так как ни у кого нет закрытого ключа.

В чём гарантия надёжности шифрования

Надёжность шифрования обеспечивается тем, что третьему лицу (старающемуся взломать шифр) очень трудно вычислить закрытый ключ по открытому. Оба ключа вычисляются из одной пары простых чисел ( p и q ). То есть ключи связаны между собой. Но установить эту связь очень сложно. Основной загвоздкой является декомпозиция модуля n на простые сомножители p и q . Если число является произведением двух очень больших простых чисел, то его очень трудно разложить на множители.

Постараюсь это показать на примере. Давайте разложим на множители число 360:

• сразу ясно, что оно делится на два (получили 2)
• оставшееся 180 тоже, очевидно чётное (ещё 2)
• 90 — тоже чётное (ещё двойка)
• 45 не делится на 2, но следующая же попытка оказывается успешной — оно делится на три (получили 3)
• 15 тоже делится на 3
• 5 — простое.

Мы на каждом шагу, практически без перебора, получали всё новые и новые множители, легко получив полное разложение 360=2×2×2×3×3×5

Давайте теперь возьмём число 361. Тут нам придётся помучиться.

• оно не чётное
• три — нет, не делится
• пять (допустим, мы поступаем умно и перебираем только простые числа, хотя, на практике, поиск больших простых чисел, сам по себе, является сложной задачей) — не подходит
• семь? — нет.
• …
• и только 19 даст нам ответ: 361=19×19.

При использовании больших чисел, задача становится очень сложной. Это позволяет надеяться, что у взломщика просто не хватит вычислительных ресурсов, чтобы сломать ваши шифр за обозримое время.

А как это всё работает на практике?

Многие читатели спрашивают, как всё это применяется на практике. Давайте рассмотрим чуть более приближенный к жизни пример. Зашифруем и расшифруем слово «КРОТ», предложенное одним из читателей. А заодно, бегло рассмотрим, какие проблемы при этом встречаются и как они решаются.

Сперва сгенерируем ключи с чуть бо́льшими числами. Они не так наглядны, но позволят нам шифровать не только числа от нуля до 20.

Оттолкнёмся от пары простых чисел = <17, 19>. Пусть наш открытый ключ будет = <5, 323>, а закрытый = <173, 323>.

Мы готовы к шифрованию. Переведём наше слово в цифровое представление. Мы можем взять просто номера букв в алфавите. У нас получится последовательность чисел: 11, 17, 15, 19.

Мы можем зашифровать каждое из этих чисел открытым ключом = <5, 323>и получить шифровку 197, 272, 2, 304. Эти числа можно передать получателю, обладающему закрытым ключом = <173, 323>и он всё расшифрует.

Немного о сложностях

На самом деле, изложенный способ шифрования очень слаб и никогда не используется. Причина проста — шифрование по буквам. Одна и та же буква будет шифроваться одним и тем же числом. Если злоумышленник перехватит достаточно большое сообщение, он сможет догадаться о его содержимом. Сперва он обратит внимание на частые коды пробелов и разделит шифровку на слова. Потом он заметит однобуквенные слова и догадается, как кодируются буквы «a», «и», «o», «в», «к»… Путём недолгого перебора, он вычислит дополнительные буквы по коротким словам, типа «но», «не», «по». И по более длинным словам без труда восстановит все оставшиеся буквы.

Таким образом, злоумышленнику не придётся отгадывать ваши секретные ключи. Он взломает ваше сообщение, не зная их.

Чтобы этого не происходило, используются специальные дополнительные алгоритмы, суть которых в том, что каждая предыдущая часть сообщения начинает влиять на следующую.

Упрощённо, это выглядит так. Перед шифрованием, мы применяем к сообщению правило: b := (b + a) % n . Где a — предыдущая часть сообщения, а b — следующая. То есть наше сообщение (11, 17, 15, 19) изменяется. 11 остаётся без изменений. 17 превращается в (11 + 17) % 323 = 28 . 15 становится (15 + 28) % 323 = 43 . A 19 превращается в 62.

Последовательность (11, 28, 43, 62) получается «запутанной». Все буквы в ней как бы перемешаны, в том смысле, что на каждый код влияет не одна буква, а все предыдущие.

Тот, кто получит ваше сообщение, должен будет проделать обратную операцию, со знаком «минус»: b := (b — a) % n . И только тогда он получит коды букв.

На практике, в исходное сообщение специально добавляются случайные и бессмысленные буквы в начало. Чтобы даже по первому коду было невозможно ничего понять. Получатель просто отбрасывает начало сообщения.

То есть мы можем добавить случайное число в начало и получить (299, 11, 17, 15, 19). После перемешивания получится: 299, 310, 4, 19, 38. После шифрования уже невозможно будет догадаться где была какая буква.

В реальной жизни всё ещё немного сложнее. Блоки, на которые бьётся сообщение длиннее одной буквы. Поэтому, сперва применяются алгоритмы выравнивания, потом алгоритмы разбиения на блоки с перепутыванием, и только потом применяется само RSA-шифрование.

Получатель делает всё в обратном порядке: расшифровывает, «распутывает» блоки и отбрасывает ненужную информацию, добавленную просто для выравнивания (чтобы сообщение можно было разбить на целое число блоков).

Детали и принципы формирования блоков можно почитать тут. Я же в этой заметке хотел рассказать только про RSA. Надесь, удалось.

Источник

Способ создания кворумных ключей схема rsa

Криптосистема [math]\mathtt[/math] стала первой системой, пригодной и для шифрования, и для цифровой подписи.

Содержание

Реализация [ править ]

Алгоритм [math]\mathtt[/math] включает в себя четыре этапа: генерация ключей, передача ключей, шифрование и расшифрование.

Криптографические системы с открытым ключом используют так называемые односторонние функции.

Определение:

Односторонняя функция (англ. one-way function) — математическая функция, которая легко вычисляется для любого входного значения, но задача нахождения аргумента по заданному значению функции относится к классу NP-полных задач.

Под односторонностью понимается не теоретическая однонаправленность, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства, за обозримый интервал времени.

В основу криптографической системы с открытым ключом [math]\mathtt[/math] положена сложность задачи факторизации произведения двух больших простых чисел. Для шифрования используется операция возведения в степень по модулю большого числа. Для дешифрования (обратной операции) за разумное время необходимо уметь вычислять функцию Эйлера от данного большого числа, для чего необходимо знать разложение числа на простые множители. В криптографической системе с открытым ключом каждый участник располагает как открытым ключом (англ. public key), так и закрытым ключом (англ. private key). В криптографической системе [math]\mathtt[/math] каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и закрытый ключ самостоятельно. Закрытый ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их. Открытый и закрытый ключи каждого участника обмена сообщениями в криптосистеме [math]\mathtt[/math] образуют «согласованную пару» в том смысле, что они являются взаимно обратными. То есть для любых допустимых пар открытого и закрытого ключей [math](p,s)[/math] существуют соответствующие функции шифрования [math]E_p(x)[/math] и расшифрования [math]D_s(x)[/math] такие, что для любого сообщения [math]m \in M[/math] , где [math]M[/math] — множество допустимых сообщений, [math]m=D_s(E_p(m))=E_p(D_s(m)).[/math]

Создание открытого и секретного ключей [ править ]

[math]\mathtt[/math] -ключи генерируются следующим образом:

1. Выбираются два различных случайных простых числа [math]p[/math] и [math]q[/math] заданного размера (например, [math]1024[/math] бита каждое).
2. Вычисляется их произведение [math]n=p\cdot q[/math] , которое называется модулем.
3. Вычисляется значение функции Эйлера от числа [math]n[/math] : [math]\varphi(n) = (p-1)\cdot (q-1).[/math]
4. Выбирается целое число [math]e[/math] ( [math]1 \lt e \lt \varphi(n)[/math] ), взаимно простое со значением функции [math]\varphi(n)[/math] . Обычно в качестве [math]e[/math] берут простые числа, содержащие небольшое количество единичных бит в двоичной записи.
   • Число [math]e[/math] называется открытой экспонентой (англ. public exponent)
   • Время, необходимое для шифрования с использованием быстрого возведения в степень, пропорционально числу единичных бит в [math]e[/math] .
   • Слишком малые значения [math]e[/math] , например [math]3[/math] , потенциально могут ослабить безопасность схемы [math]\mathtt[/math] .
5. Вычисляется число [math]d[/math] , мультипликативно обратное к числу [math]e[/math] по модулю [math]\varphi(n)[/math] , то есть число, удовлетворяющее сравнению: [math]d\cdot e \equiv 1 \pmod<\varphi(n)>.[/math] Примечание Сравнеие двух целых чисел по модулю натурального числа [math]m[/math] — математическая операция, позволяющая ответить на вопрос о том, дают ли два выбранных целых числа при делении на [math]m[/math] один и тот же остаток. Любое целое число при делении на [math]m[/math] дает один из [math]m[/math] m возможных остатков: число от [math]0[/math] до [math]m-1[/math] .
   • Число [math]d[/math] называется секретной экспонентой. Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.
6. Пара [math]\left\< e, n \right\>[/math] публикуется в качестве открытого ключа [math]\mathtt[/math] (англ. [math]\mathtt[/math] public key).
7. Пара [math]\left\< d, n \right\>[/math] играет роль закрытого ключа [math]\mathtt[/math] (англ. [math]\mathtt[/math] private key) и держится в секрете.

Определение:

Случайное простое число (англ. random prime numbers) — в криптографии, простое число, содержащее в двоичной записи заданное количество битов.

Передача ключей [ править ]

Предположим, что Боб хочет отправить Алисе информацию . Если они решат использовать [math]\mathtt[/math] , Боб должен знать открытый ключ Алисы для того чтобы зашифровать сообщение, а Алиса должна использовать свой закрытый ключ для расшифрования сообщения. Чтобы позволить Бобу отправлять свои зашифрованные сообщения, Алиса передает свой открытый ключ Бобу через надежный, но не обязательно секретный маршрут. Закрытый ключ Алисы никогда никому не передается.

Шифрование [ править ]

Предположим, Боб хочет послать Алисе сообщение [math]m[/math] . Сообщениями являются целые числа в интервале от [math]0[/math] до [math]n — 1[/math] , то есть [math]m \in \mathbb_[/math] . Алгоритм:

• Взять открытый ключ [math](e,n)[/math] Алисы
• Взять открытый текст [math]m[/math]
• Зашифровать сообщение с использованием открытого ключа Алисы: [math]c = E(m) = m^e \mod n

Расшифрование [ править ]

• Принять зашифрованное сообщение [math]c[/math]
• Взять свой закрытый ключ [math](d,n)[/math]
• Применить закрытый ключ для расшифрования сообщения: [math]m = D(c) = c^d \mod n

Корректность схемы [math]\mathtt[/math] [ править ]

Доказательство: [math]\triangleright[/math]

Действительно, для [math]\forall m \in \mathbb_[/math]

[math]\forall m \in \mathbb_: m^ \equiv m \pmod

[/math] .

Возможны два случая:

Поскольку числа [math]e[/math] и [math]d[/math] являются взаимно обратными относительно умножения по модулю [math]\varphi(n)=(p-1)(q-1)[/math] , то есть

[math]ed=1+k(p-1)(q-1)[/math] для некоторого целого [math]k[/math] ,

[math]\begin m^ & \equiv m^ <1 + k\left(

\right)\left( \right)> \pmod

\\ & \equiv m\left( > \right)^ \right)> \pmod

\\ & \equiv m\left( 1 \right)^ \right)> \pmod

\equiv m \pmod

\end[/math]

где второе тождество следует из теоремы Ферма.

• Рассмотрим второй случай:

[math]m \equiv 0 \pmod

[/math] , то есть [math]m[/math] кратно [math]p[/math] . Значит, [math]m^[/math] кратно [math]p[/math] ,

[math]m^ \equiv 0 \pmod

\equiv m \pmod

[/math]

Таким образом, при всех [math]m[/math] выполняется равенство

[math]m^ \equiv m \pmod

[/math]

Аналогично можно показать, что:

[math]\forall m \in \mathbb_: m^ \equiv m \pmod[/math] .

[math]\forall m \in \mathbb_: m^ \equiv m \pmod[/math] [math]\triangleleft[/math]

Криптографическая стойкость [ править ]

Стойкость алгоритма основывается на сложности вычисления обратной функции к функции шифрования

[math]c = E(m) = m ^ e \mod n[/math] .

Для вычисления [math]m[/math] по известным [math]c, e, n[/math] нужно найти такой [math]d[/math] , чтобы

[math]e \cdot d \equiv 1 \pmod<\varphi(n)>,[/math]

Вычисление обратного элемента по модулю не является сложной задачей, однако злоумышленнику неизвестно значение [math]\varphi(n)[/math] . Для вычисления функции Эйлера от известного числа [math]n[/math] необходимо знать разложение этого числа на простые множители. Нахождение таких множителей и является сложной задачей, а знание этих множителей — «потайной дверцей» (англ. backdoor), которая используется для вычисления [math]d[/math] владельцем ключа. Существует множество алгоритмов для нахождения простых сомножителей, факторизации, самый быстрый из которых на сегодняшний день — общий метод решета числового поля, скорость которого для k-битного целого числа составляет

[math] \exp (( c + o(1))k^<\frac<1><3>> \log^<\frac<2><3>>k)[/math] для некоторого [math]c \lt 2[/math] .

В [math]2010[/math] году группе учёных из Швейцарии, Японии, Франции, Нидерландов, Германии и США удалось успешно вычислить данные, зашифрованные при помощи криптографического ключа стандарта [math]\mathtt[/math] длиной [math]768[/math] бит. Нахождение простых сомножителей осуществлялось общим методом решета числового поля. По словам исследователей, после их работы в качестве надежной системы шифрования можно рассматривать только [math]\mathtt[/math] -ключи длиной [math]1024[/math] бита и более. Причём от шифрования ключом длиной в [math]1024[/math] бит стоит отказаться в ближайшие три-четыре года. С [math]31[/math] декабря [math]2013[/math] года браузеры Mozilla перестали поддерживать сертификаты удостоверяющих центров с ключами [math]\mathtt[/math] меньше [math]2048[/math] бит.

Применение [ править ]

Система [math]\mathtt[/math] используется для защиты программного обеспечения и в схемах цифровой подписи. Также она используется в открытой системе шифрования PGP [1] и иных системах шифрования (к примеру, DarkCryptTC [2] и формат xdc [3] ) в сочетании с симметричными алгоритмами.

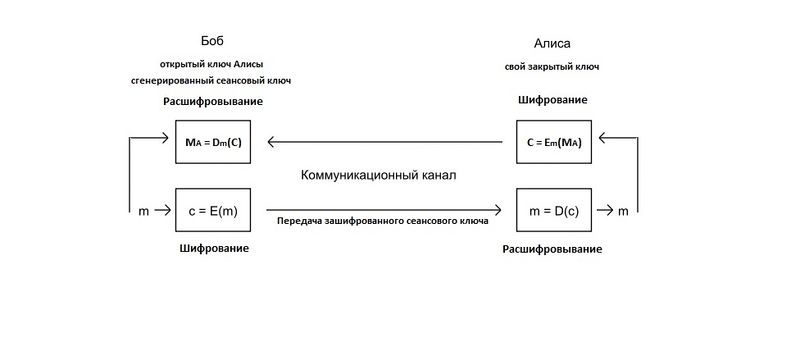
Наиболее используемым в настоящее время является смешанный алгоритм шифрования, в котором сначала шифруется сеансовый ключ, а потом уже с его помощью участники шифруют свои сообщения симметричными системами. После завершения сеанса сеансовый ключ, как правило, уничтожается.

Алгоритм шифрования сеансового ключа выглядит следующим образом:

Шифрование [ править ]

• Взять открытый ключ [math](e,n)[/math] Алисы
• Создать случайный сеансовый ключ [math]m[/math]
• Зашифровать сеансовый ключ с использованием открытого ключа Алисы: [math]c = E(m) = m^e \mod n[/math]
• Расшифровать сообщение [math]C[/math] с помощью сеансового ключа симметричным алгоритмом: [math]M_A = D_m(C)[/math]

Расшифрование [ править ]

• Принять зашифрованный сеансовый ключ Боба [math]c[/math]
• Взять свой закрытый ключ [math](d,n)[/math]
• Применить закрытый ключ для расшифровывания сеансового ключа: [math]m = D(c) = c^d \mod n[/math]
• Зашифровать сообщение [math]M_A[/math] с помощью сеансового ключа симметричным алгоритмом: [math]C = E_m(M_A)[/math]

Минусы [ править ]

Алгоритм [math]\mathtt[/math] намного медленнее, чем AES [4] и другие алгоритмы, использующие симметричные блочные шифры.

При неправильной или неоптимальной реализации или использовании алгоритма возможны специальные криптографические атаки, такие как атаки на схемы с малой секретной экспонентой или на схемы с общим выбранным значением модуля.

Из-за низкой скорости шифрования (около [math]30[/math] кбит/с при [math]512[/math] битном ключе на процессоре [math]2[/math] ГГц), сообщения обычно шифруют с помощью более производительных симметричных алгоритмов со случайным сеансовым ключом (например, IDEA [5] , Serpent [6] , Twofish [7] ), а с помощью [math]\mathtt[/math] шифруют лишь этот ключ, таким образом реализуется гибридная криптосистема.

Источник