Способ совмещения начертательная геометрия

Способ совмещения

Вращение плоскости вокруг оси, совпадающей с плоскостью проекций, т.е. вокруг следа плоскости, является частным случаем вращения вокруг линии уровня плоскости.

Способ совмещения заключается в том, что заданную плоскость Р вместе с расположенными в ней геометрическими элементами вращают вокруг одного из ее следов Р_Н или Р_V до совмещения с соответствующей плоскостью проекций Н или V.

Все геометрические элементы (прямые и другие линии, фигуры), лежащие в заданной плоскости, изображаются в натуральную величину на плоскости проекций, с которой производится совмещение. Совмещение позволяет найти величину плоской фигуры по ее проекциям или построить проекции плоской фигуры, лежащей в какой-либо плоскости, по заданным ее размерам.

Если плоскость задана следами, то задача совмещения ее с плоскостью проекций сводится к построению совмещенного положения одного из следов, так как другой след, принимаемый за ось вращения, не меняет своего положения.

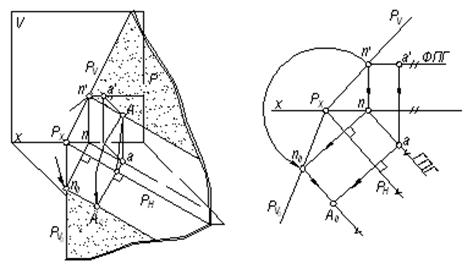
Как видно из рис. 5.14, для определения совмещенного следа Pv₀ при вращении плоскости Р вокруг следа Р_H достаточно найти совмещенное положение N₀ любой точки N следа Р_V. На рис. 5.14 показано также совмещение точки А (а, а’), лежащей в плоскости Р,с плоскостью Н при использовании горизонтали.

Задача.Найти натуральную величину треугольника ABC,расположенного в плоскости Р общего положения (рис. 5.15).

Плоскость Р совмещаем с плоскостью Н вращением вокруг следа Р_Н.. Используя горизонтали плоскости, на которых лежат вершины треугольника, находим совмещенные положения А₀, В₀, С₀ этих вершин и получаем треугольник А₀В₀С₀, равный заданному.

Источник

Способ совмещения

Способ плоскопараллельного перемещения.

Применение способа вращения часто приводят к тому, что преобразованная проекция фигуры накладывается на заданную. Построение и чтение такого чертежа затрудняется.

Этого недостатка лишен способ плоскопараллельного перемещения. Так называют плоское движение геометрического объекта, при котором все ее точки движутся параллельно некоторой плоскости.

Этот способ является частным случаем способа вращения. Свойства проекций, указанные в способе вращения, позволяют производить вращение объекта, не нанося на чертеже оси вращения, а выбирая только ее направление (рис.33).

Рис. 33

Частным случаем способа вращения является совмещение.

Совмещением называется вращение плоскости вокруг одного из ее следов до совмещения этой плоскости с плоскостью проекций. Этот прием целесообразно применять для определения действительных размеров плоских фигур, расположенных в плоскостях, заданных следами.

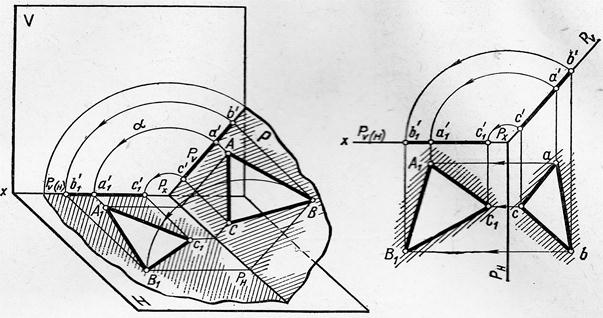
Если фронтально проецирующую плоскость Р (рис. 34) повернуть вокруг ее горизонтального следа Р_н на угол α, то она совместится с горизонтальной плоскостью проекции Н. Расположенный в плоскости Р треугольник АВС также совместиться с плоскостью Н и изобразиться на ней без искажения.

Рис. 34

Фронтальный след Р_v при совмещении Р с Н займет положение Р_v(н) – сольется с осью x. Так как в данном случае вращение осуществляется вокруг оси, перпендикулярной к плоскости проекции V (след Р_н перпендикулярен к плоскости V), то фронтальные проекции аʹ, bʹ, cʹ точек, лежащих в плоскости Р, будут перемещаться по окружности , а их горизонтальные проекции a, b – по прямым, перпендикулярным к оси вращения Р_н. При совмещении плоскостей Р и Н фронтальные на оси x — aʹ₁ bʹ₁ cʹ₁, а горизонтальные займут положение А_1, В₁, С₁.

Получившаяся при этом фигура А₁В₁С₁ равна треугольнику АВС, расположенному в плоскости Р.

Рис. 35.

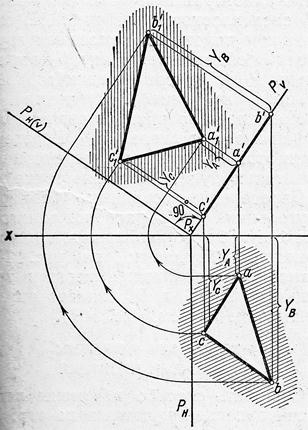
Указанную задачу можно решить вращением плоскости Р вокруг ее фронтального следа Р_v до совмещения с плоскостью V (рис. 35) .

Контрольные вопросы

1. В чем заключается сущность способов вращения и перемены плоскостей проекций? С какой целью используют указанные способы в начертательной геометрии и черчении?

2. Как перемещаются фронтальная и горизонтальная проекции точки при вращении ее вокруг оси, перпендикулярной к плоскости Н?

3. Что такое совмещение? В каких случаях целесообразно использовать этот прием?

4. В чем заключается способ плоскопараллельного перемещения?

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Способ совмещения начертательная геометрия

Нахождение натуральной величины способом совмещения

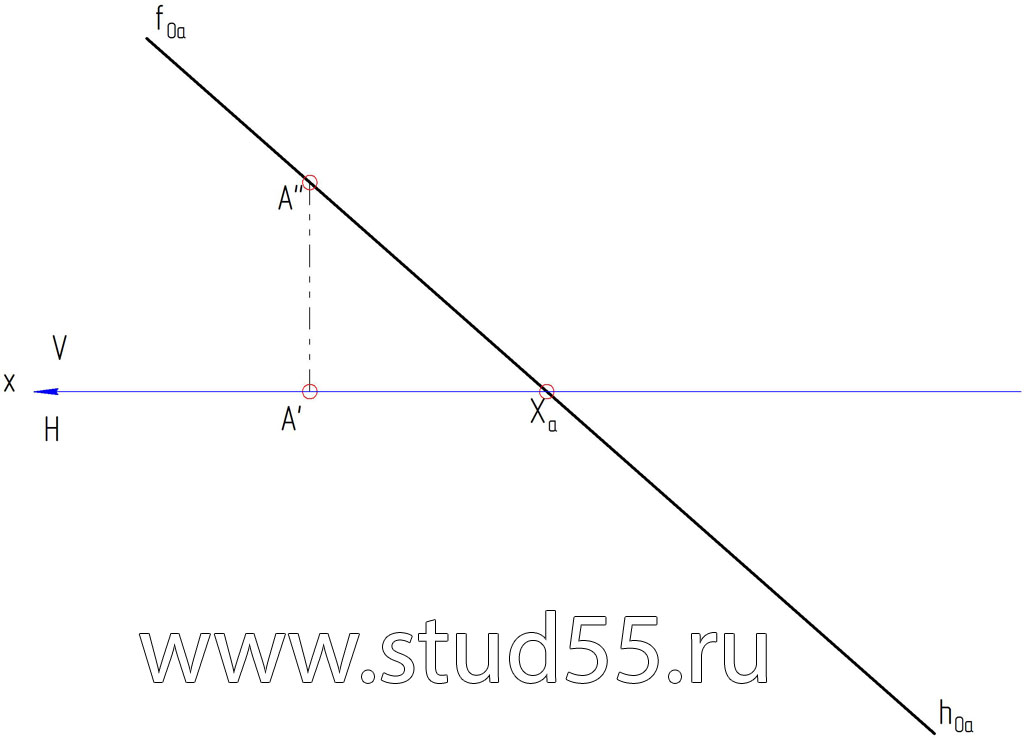
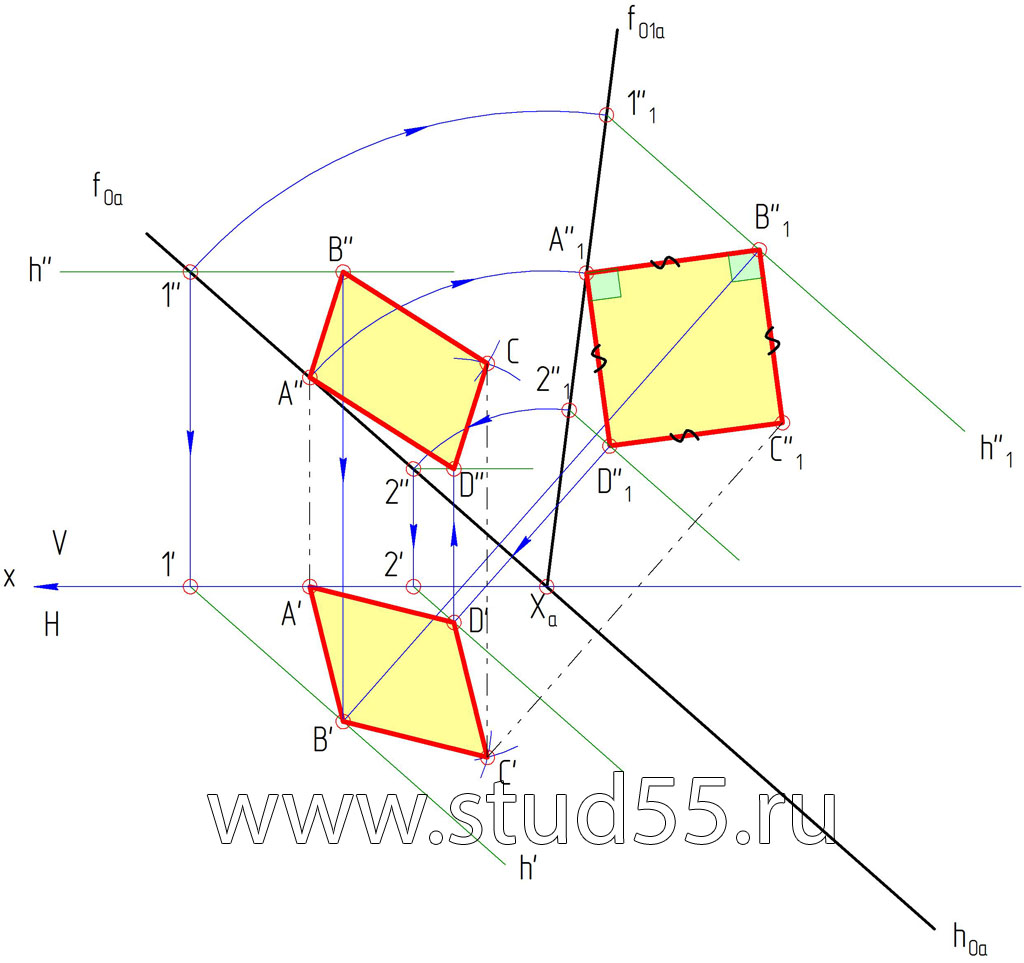
Задача: В плоскости, заданной следами, взять произвольный отрезок АВ. Способом совмещения определить его истинную величину. Принимая отрезок за сторону правильной плоской фигуры (квадрат), построить эту фигуру.

Теория

Способ совмещения заключается в том, что заданную плоскость а (альфа) вместе с расположенными в ней геометрическими элементами вращают вокруг одного из ее следов f_oa или h_oa до совмещения с соответствующей плоскостью проекций Н или V.

Все геометрические элементы (прямые и другие линии, фигуры), лежащие в заданной плоскости, изображаются в натуральную величину на плоскости проекций, с которой производится совмещение. Совмещение позволяет найти величину плоской фигуры по ее проекциям или построить проекции плоской фигуры, лежащей в какой-либо плоскости, по заданным ее размерам.

Пошаговое решение:

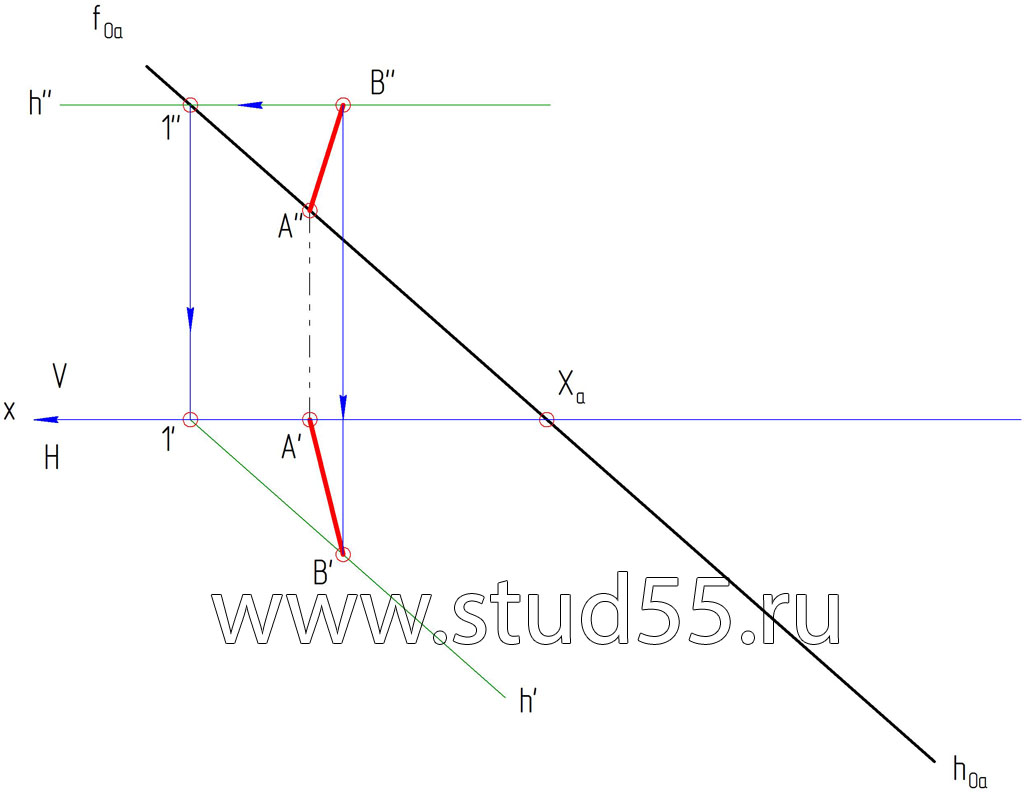
1) Берем произвольную проекцию точки В (B») во фронтальной плоскости V, находим ее проекцию B’ горизонтальной плоскости проекций Н, из у словия, что отрезок АВ лежит в плоскости альфа.

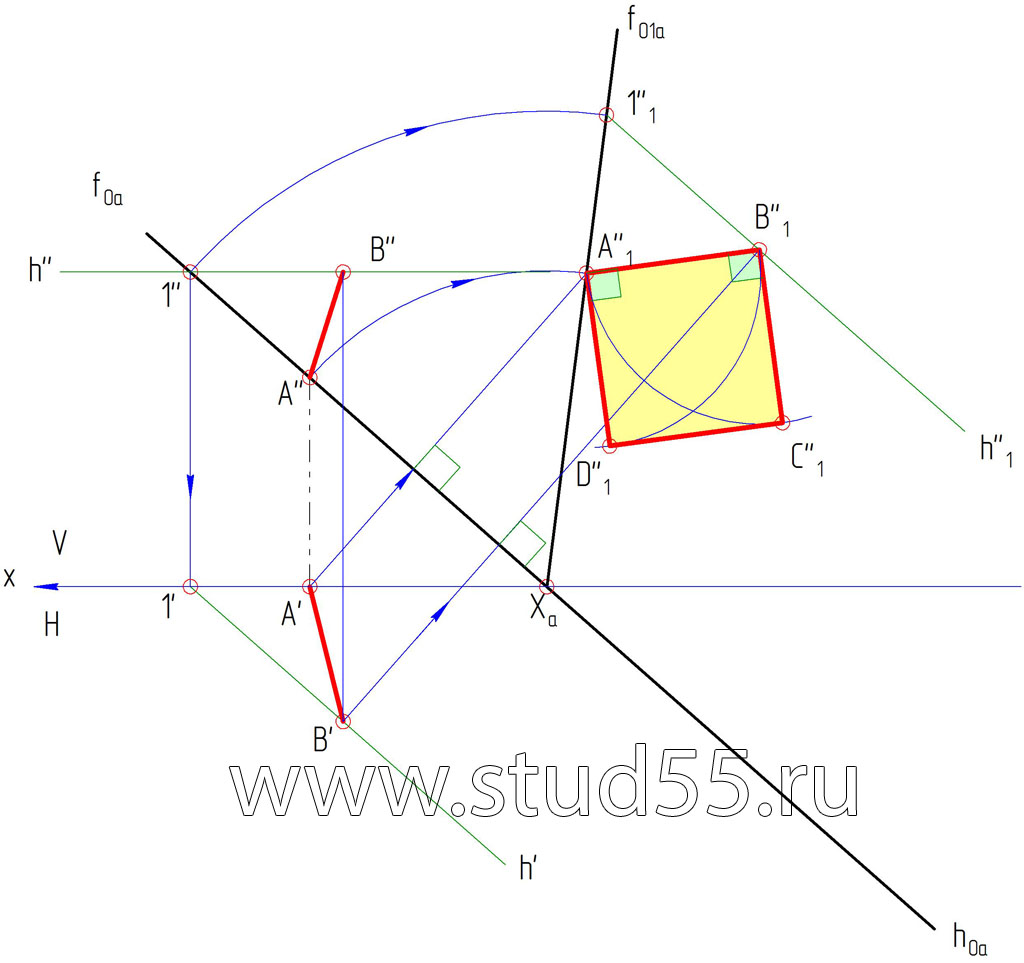
2) Т.к. плоскость задана следами, то задача совмещения ее с плоскостью проекций сводится к построению совмещенного положения одного из следов — f_o1a, так как другой след — h_oa, принимаемый за ось вращения, не меняет своего положения.

Отрезок АВ, лежащий в заданной плоскости, изображается в истинную величину (И.в.) на новой плоскости проекций, с которой мы произвели совмещение.

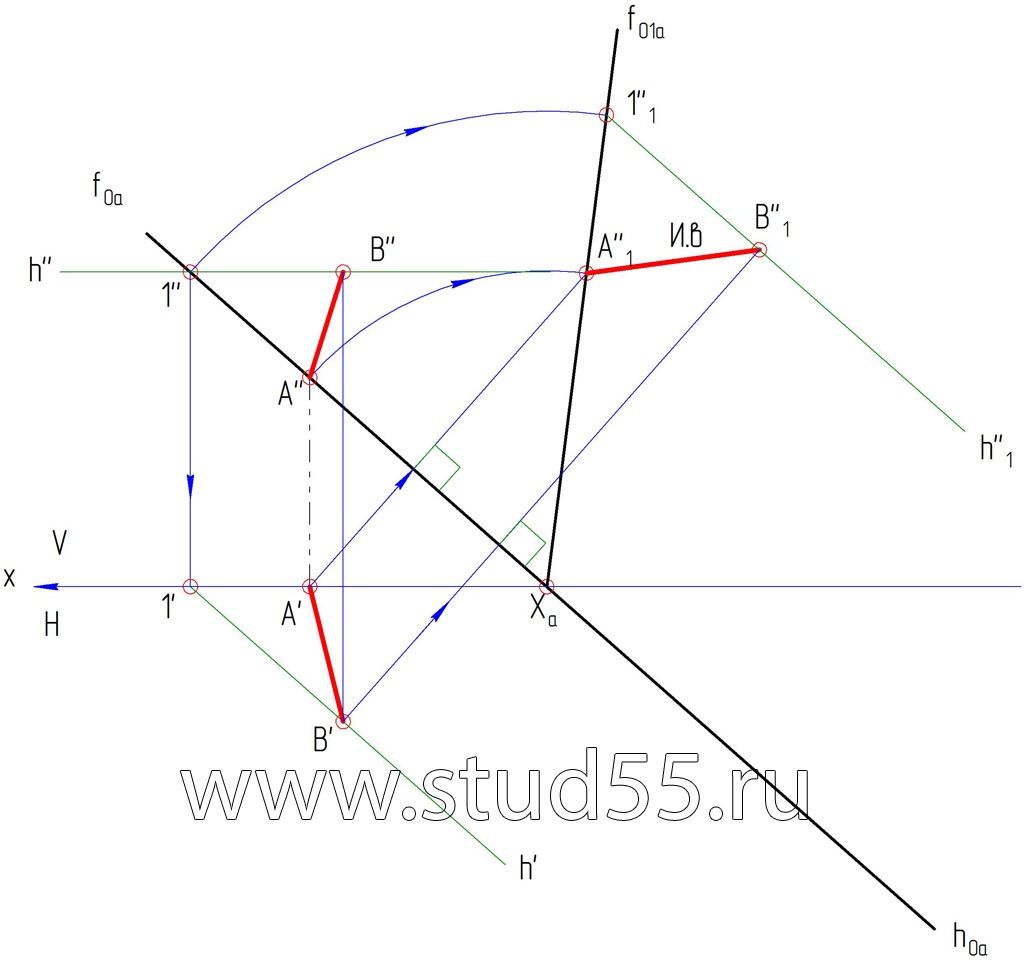
3) В совмещенной плоскости достраиваем искомую фигуру (квадрат со стороной АВ).

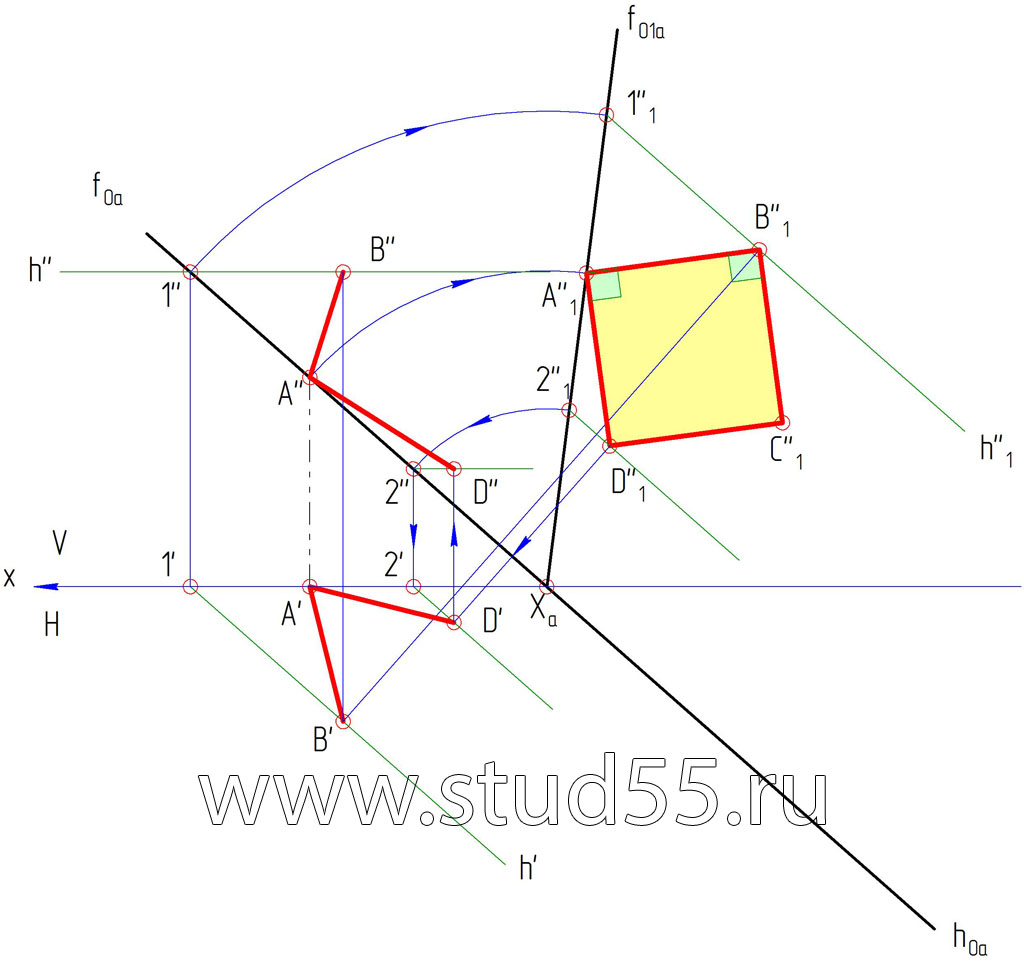
4) В совмещенной плоскости проводим горизонталь через проекцию точки D ( D»1), обратным вращением при помощи точки 2, находим горизонталь в плоскостяи проекций V, затем в H, а также проекции точки D — D’, затем по линии связи — D».

5) Проекции точки С (С» и C’) можно найти аналогичным способом, также как и нахождение точки D, или простыми построениями параллелограммов (квадрат отображается в виде параллелограмма).

У кого есть вопросы, пишите в комментариях!

Источник

9.5. Метод совмещения плоскостей

Этот метод является частным случаем метода вращения вокруг линии уровня. В качестве оси вращения выбирается линия пересече­ния плоскости, в которой лежит та или иная фигура, с одной из плос­костей проекций. Иначе говоря, осью вращения служит горизонталь­ный или фронтальный след плоскости. При этом каждая точка, при­надлежащая рассматриваемой фигуре, при вращении перемещается в плоскости, перпендикулярной к следу той плоскости, в которой она лежит. Например, плоскость , заданную своими следами и , не­обходимо совместить с горизонтальной плоскостью проекций П₁ (рис. 9.7).

Для решения поставленной задачи берут на фронтальном следе плоскостипроизвольную точку 1₂ и находят ее горизонтальную проекцию 1, которая лежит на оси х. Далее из точки 1₁ проводят луч, перпендикулярный к горизонтальному следу плоскости (любаяточка при вращении должна перемещаться в плоскости, перпендику­лярной к оси поворота). На нем находят совмещенное положение точ­ки 1 — точку 1₀, как точку пересечения луча с дугой окружности радиусом . Точка 1₀ принадлежит одновременно и плоскости П₁ и новому (совмещенному) положению плоскости . Через точку 1₀ проводят новый фронтальный след ₀ плоскости . Следы ₁ и ₀ ха­рактеризуют новое (совмещенное) положение плоскости .

9.6. Вопросы для самопроверки

В чем состоит сущность преобразования ортогональных проек­ций способом замены плоскостей проекций?

Сколько замен плоскостей проекций и в какой последователь­ности необходимо выполнить, чтобы перевести отрезок прямой обще­го положения в отрезок прямой частного положения?

Сколько замен плоскостей проекций и в какой последователь­ности необходимо выполнить, чтобы определить натуральную вели­чину плоской фигуры?

В чем заключается способ вращения вокруг проецирующейоси?

В каких плоскостях перемещается точка, вращаемая вокруг оси, перпендикулярной к плоскостям П₁ и П₂?

Сущность способа плоскопараллельного перемещения.

Что представляет собой преобразование чертежа способом вра­щения вокруг линии уровня?

В чем заключается преобразование чертежа способом совмеще­ния?

9.7. Примеры решения задач

Ниже приведены решения одной и той же задачи вышеописанны­ми методами.

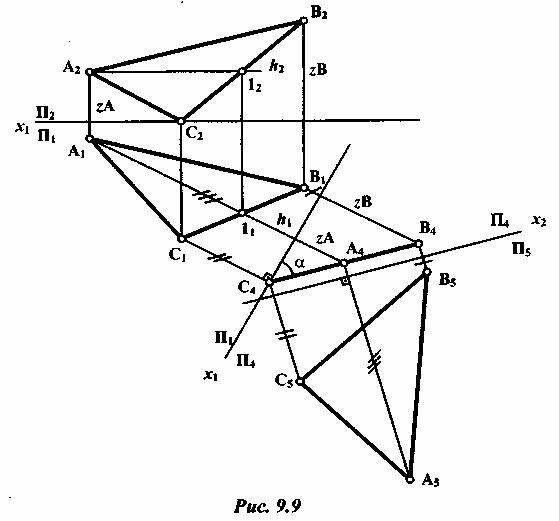
1) Решение методом замены плоскостей проекций (рис. 9.9).

Плоскость треугольника спроецируется в натуральную величину в том случае, если она будет в пространстве параллельна одной из плоскостей проекций. Одним преобразованием задачу решить невоз­можно. Она решается в два этапа: при первой замене плоскостей про­екций получают плоскость треугольника ABC, перпендикулярную к новой плоскости проекций, при второй замене — получают плоскость треугольника, параллельную новой плоскости проекций.

Первый этап. Одним из условий перпендикулярности двух плос­костей является наличие прямой, принадлежащей одной из плоско­стей, перпендикулярной к другой плоскости. Используя этот признак, проводят через точку А в плоскости треугольника горизонталь (h). За­тем на произвольном расстоянии от горизонтальной проекции тре­угольника A₁B₁C₁ проводят ось x₁ новой системы плоскостей проек­ций П₁/П₄ перпендикулярно к горизонтальной проекции горизонта­ли h₁. В новой системе треугольник ABC стал перпендикулярен к но­вой плоскости проекций П₄.

На линиях проекционной связи в новой системе откладывают ко­ординаты z точек А, В, С с фронтальной проекции исходной системы плоскостей П₁/П₂. При соединении новых проекций А₄, B₄, С₄ полу­чают прямую линию, в которую спроецировалась плоскость тре­угольника ABC. На этом этапе определяется угол наклона плоскости треугольника к горизонтальной плоскости проекции П₁ — угол . Начертеже это угол между осью x₁ и проекцией С₄А₄В₄.

Второй этап. Выбираем новую плоскость проекции П₅, парал­лельную плоскости треугольника, т.е. новую ось x₂ проводят парал­лельно С₄А₄В₄ на произвольном расстоянии. Получают новую систе­му П₄/П₅. Полученный треугольник А₅В₅С₅ и есть искомая натураль­ная величина треугольника ABC.

2) Решение методом вращения вокруг проецирующей оси

Задача решается в два этапа. На первом этапе выполняют враще­ние так, чтобы плоскость треугольника ABC преобразовалась в проецирующую плоскость, т.е. стала перпендикулярна к одной из плос­костей проекций. Для этого на фронтальной проекции чертежа прово­дят горизонталь h₂ через точку А₂. Затем строят горизонтальную про­екцию h₁ горизонтали h через точки A₁ и 1₁ Через точку 1 проводят ось i — ось вращения треугольника так, чтобы она была перпендику­лярна к П₁. На фронтальной проекции через вершины А₂ и В₂ прово­дят горизонтальные плоскости уровня ₂ и ₂. Вершина С принадле­жит плоскости П₁ поэтому ее плоскостью вращения будет плоскость проекций П₁. На горизонтальной проекции, взяв за центр вращения проекцию i₁ поворачивают горизонталь А так, чтобы на плоскость П₂ она спроецировалась в точку. На чертеже это выразится тем, что h’₁ займет новое положение — перпендикулярно к оси х. При этом на фронтальной проекции точка А₂ перемещается по следу плоскости ₂ до пересечения с линией связи, проведенной через точку a’₁. На гори­зонтальной проекции поворачиваем оставшиеся вершины В и С во­круг оси так, чтобы . На фронтальной проекциивершина В перемещается по следу плоскости ₂, а вершина С — по оси х. Соединив новое положение всех вершин треугольника ABC, получают проекцию А’₂В’₂С’₂, сливающуюся в линию. Этим достига­ют проецирующего положения треугольника ABC. На данном этапе, при необходимости, находят угол наклона плоскости треугольника ABC к П₁ — .

На втором этапе проводят ось i` через вершину С так, чтобы ось была фронтально проецирующая. При этом С’<sub>2</sub> = /’<sub>2</sub>, а горизонтальная проекция i’<sub>1</sub> пройдет через проекцию С’<sub>1</sub>. Вокруг оси поворачивают треугольник так, чтобы он стал параллелен горизонтальной плоскости проекций. В данной задаче вращают точки А’<sub>2</sub> и В’<sub>1</sub>, вокруг i`₂ = С’₂ до совмещения с осью х, при этом горизонтальные проекции B’₁ и A’₁ будут перемещаться в горизонтально проецирующихся плоскостях уровня иP₁ и займут новое положение В»₁, и А»₁ вершина С оста­нется на месте. Соединив новые точки между собой, получают тре­угольник ABC в натуральную величину.

3) Решение методом плоскопараллельного перемещения (рис. 9.11).

Задача решается в два этапа. На первом этапе преобразовывают чертеж так, чтобы плоскость треугольника ABC стала перпендику­лярна к одной из плоскостей проекций, т.е. должна в себе содержать прямую, перпендикулярную к этой плоскости. Для этого проводят в

плоскости треугольника горизонталь h (фронтальная проекция А₂1₂ // х, а горизонтальная — A₁1₁). Каждую вершину треугольника заключают в свою плоскость уровня, параллельную плоскости П₁. В рассматриваемом примере вершина С принадлежит плоскости проек­ций П₁, А принадлежит плоскости , а В — плоскости А.

Плоскость треугольника перемещается в пространстве до тех пор, пока горизонталь h₁ треугольника не станет перпендикулярна к фрон­тальной плоскости проекций П₂. Для этого на произвольном расстоя­нии от оси х вычерчивают горизонтальную проекцию треугольника A₁B₁C₁ с условием, что П₂, а значит х. При этом вер­шины треугольника, перемещаясь каждая в своей плоскости, займут новое положение — А’₂В’₂С’₂. Соединив эти точки, получают новое положение треугольника ABC, спроецированного в линию, т.е. пер­пендикулярного к плоскости П₂.

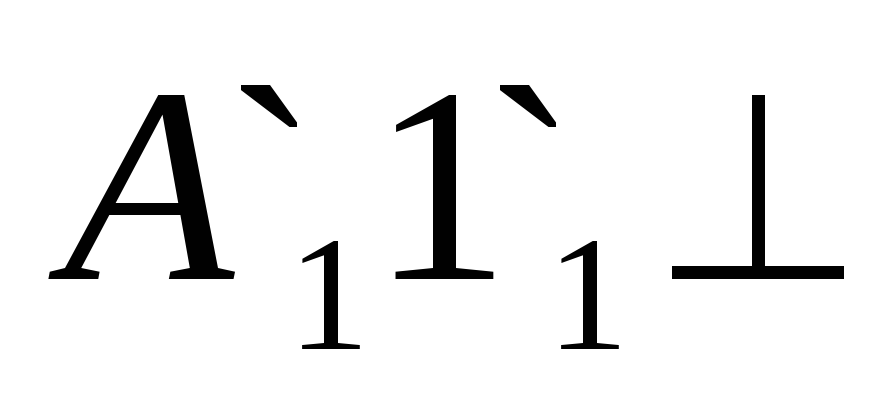
На втором этапе, чтобы получить натуральную величину тре­угольника ABC, его плоскость поворачивают до тех пор, пока она не будет параллельна одной из плоскостей проекций. В рассматриваемом решении фронтальную проекцию треугольника А’₂В’₂С’₂ располагают на произвольном расстоянии от оси х параллельно плоскости П₁. При этом вершины А, В и С треугольника заключают в горизонтально проецирующие плоскости , Т, Р. По следам этих плоскостей будутперемещаться горизонтальные проекции вершин А’₁ В’₁ С’₁. От но­вого положения фронтальной проекции А»₂В»₂С»2 проводят линии проекционной связи до пресечения с соответствующими следами плоскостей, в которых они перемещаются (,T₁,P₁), и получают точки А»₁ В»₁ C»₁. Соединив эти точки между собой, получают тре­угольник ABC в натуральную величину.

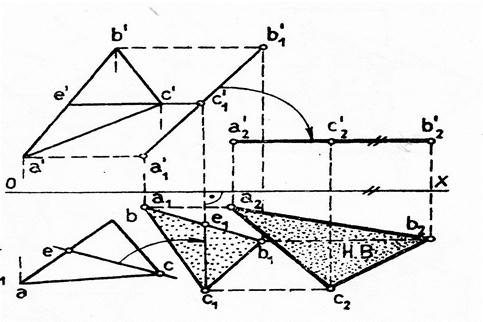
4) Решение методом вращения вокруг линии уровня (рис. 9.12).

Для решения задачи этим способом необходимо повернуть плос­кость треугольника вокруг линии уровня, в данном случае вокруг го­ризонтали, в положение, параллельное горизонтальной плоскости проекции. Через точку А в плоскости треугольника ABC проводят го­ризонталь h, фронтальная проекция которой будет параллельна оси х. Отмечают точку 1₂ и находят ее горизонтальную проекцию 1₁. Пря­мая A₁1₁ является горизонтальной проекцией h₁ горизонтали h. Во­круг горизонтали будут вращаться точки В и С. Для определения ра­диуса вращения точки С на горизонтальной проекции проводят перпендикуляр C₁O₁ 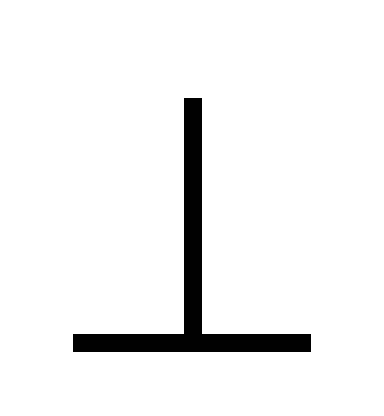A₁1₁ точка О₁, является центром вращения точ­ки С.

Для определения натуральной величины радиуса вращения строят прямоугольный треугольник, в котором O₁C₁ — один из катетов. Вто­рой катет — разность координат отрезка О₂С₂, взятого с фронталь­ной проекции. В построенном треугольнике гипотенуза O₁C₀ — нату­ральная величина радиуса вращения.

На продолжении перпендикуляра O₁C₁ откладывают |R_Bp.| и полу­чают новое положение вершины С после вращения — С₀. Вторая вер­шина В₀ получается пересечением луча C₀1₁ и перпендикуляра к горизонтальной проекции h₁ проведенного через точку b₁.

Треугольник A₁B₀C₀ есть искомая натуральная величина тре­угольника ABC.

5) Решение методом совмещения (рис. 9.13).

Для решения задачи методом совмещения необходимо построить следы плоскости , которой принадлежит треугольникABC. Для этого проводят в плоскости треугольника ABC фронталь и находят го­ризонтальный след этой фронтали – N₁. По условию задачи верши­на С треугольника принадлежит горизонтальной плоскости проек­ций П₁. Тогда горизонтальный след плоскости проводят через точки n₁ и C₁. Соединив эти две точки и продлив отрезок до пересе­чения с осью х, находят точку схода следов . Учитывая свойство, что все фронтали плоскости параллельны ее фронтальному следу, фронтальный след ₂ плоскости проводят через точку парал­лельно фронтали .

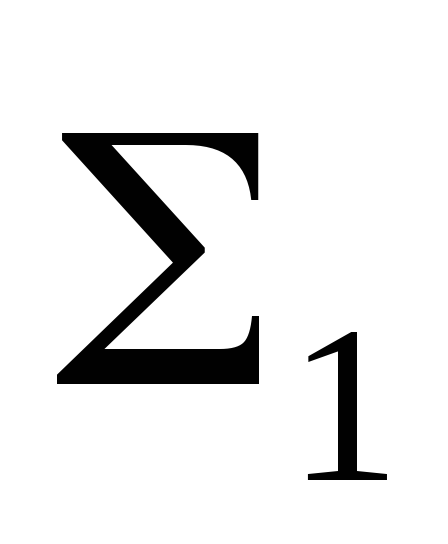
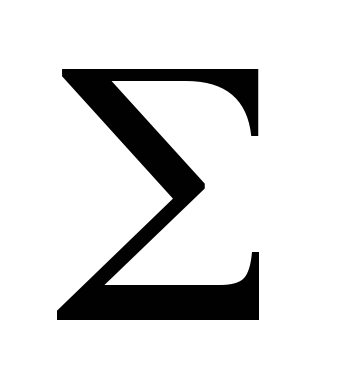
Для нахождения натуральной величины треугольника ABC необ­ходимо построить совмещенное положение плоскости с горизон­тальной плоскостью проекций П₁. Для этого через вершину А прово­дят горизонталь h₁. На фронтальном следе ₂ фиксируют точку 2₂. Ее горизонтальная проекция — точка 2₁. Точка 2 вращается в плоскости, перпендикулярной к горизонтальному следу плоскости . Поэтому,чтобы построить точку 2 в совмещенном положении 2₀, проводят из 2₁ перпендикуляр к горизонтальному следу , а из центрадугу ок­ружности радиусом до пересечения с направлением перпендику­ляра. Соединив с 2₀, получают совмещенное положение фронталь­ного следа — Далее через точку 2_о проводят горизонталь h_a в совме­щенном положении. На этой горизонтали находят точку А₀, проведя перпендикуляр из точки a₁ к горизонтальному следу .

По такой же схеме строят совмещенное положение точки В₀. Со­вмещенное положение точки С совпадает с ее горизонтальной проек­цией С₁ т.е. . Соединив построенные точки, получают тре­угольник А₀В₀С₀ — это и есть натуральная величина треугольника ABC.

Источник