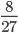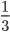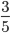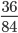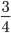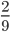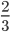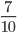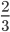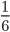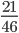Способ сокращения дроби видеоурок

Видеоурок «Основное свойство дроби. Сокращение дробей».

Сократить дробь — значит, используя основное свойство дроби, уменьшить числитель и знаменатель так, что бы величина дроби при этом не изменилась. Для сокращения дробей достаточно использовать основное свойство дроби, уменьшая числитель и знаменатель в одинаковое число раз.

Правило. Сократить дробь — значит, числитель и знаменатель дроби разделить на одинаковый множитель, отличный от 1, в результате деления дробь записывается числами, величина которых меньше во столько раз, какова величина делителя.

Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями!

	Сергей Кравцов рассказал о проекте по обновлению правил русского языка
	В Министерстве просвещения разработали меморандум по воспитательной работе в школах
	Поздравляем с наступающим Днём учителя!
	В Минпросвещения и Рособрнадзоре уже провели работу по снижению количества контрольных работ в школах
	Бесплатный вебинар «Дети в Интернете. Все, что нужно знать о контентной фильтрации в образовательных учреждениях»

Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала.

© 2007 — 2021 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель: Никитенко Евгений Игоревич

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте (презентации, конспекты, статьи и пр.), пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьими лицами.

Администрация сайта готова оказать поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Использование материалов сайта возможно только с разрешения администрации портала.

Фотографии предоставлены

Источник

Видеоурок 6 Класс Сокращение Дробей

6 класс, 9 урок, Сокращение дробей

Решаем задачи(упражнения) на заказ (!). P.S. Если хочешь решать задачи и при этом зарабатывать, то напиши нам на whatsaap: +7(707)7328227 .

МАТЕМАТИКА 6 класс: Сокращение дробей | Видеоурок

Сокращением дроби называется деление её числителя и знаменателя на их общий делитель. Сократить дробь — значит получить дробь, равную .

Сокращение дробей. 6 класс

Участвуйте в конкурсе! Подробнее об условиях Поддержать канал: .

СОКРАЩЕНИЕ ДРОБЕЙ. Видеоурок | МАТЕМАТИКА 6 класс

Разъясняются методы сокращения обыкновенных дробей на основе основного свойства дробей по курсу «Виленкин Н. Я. и др. Математика. 6 класс» и .

Математика 6 класс. 1 октября. Сокращение дробей

Сказки Андрея! Канал с моими авторскими сказками: Если вам нужен канал для другого .

Сокращение дробей | Математика 6 класс #9 | Инфоурок

Видеоуроки являются идеальными помощниками при изучении новых тем, закреплении материала, для обычных и факультативных занятий, для .

Как сокращать дроби просто. Математика 6 класс

Вы узнаете о двух способах сокращения дробей, вспомните, как раскладывать число на простые множители.

Основное свойство дроби. Сокращение дробей. 5 класс.

дроби #сокращениедробей #MEKTEП_OnLine #MEKTEP_OnLine МЕКТЕП OnLine — образовательный проект! Эльмира Рафикова — преподаватель .

Сокращение дробей часть 1. Математика 5 класс.

Сказки Андрея! Канал с моими авторскими сказками: Если вам нужен канал для другого .

#6КЛАСС. #СОКРАЩЕНИЕ #ДРОБЕЙ

Урок на тему: «Сокращение дробей» Разбор темы на простых примерах Страница вконтакте⤵️ Страница в instagram ⤵️ .

Математика 6 класс. 2 октября. Сокращение дробей 2

Сказки Андрея! Канал с моими авторскими сказками: Если вам нужен канал для другого .

Сокращение дробей. Математика 6 класс

Основное свойство дроби и сокращение дробей. Разбор заданий на примерах. PS: прошу прощения за качество видео, пока ещё примеряюсь как .

Сокращение дробей | Примеры

Сокращение дробей — примеры. Посмотрите это видео и научитесь сокращать дроби легко и просто. #математика.

Сокращение дробей. 5 — 6 класс.

В данном видео разбираем тему и примеры из учебника по математике для 6 класса, автор Мерзляк А.Г., расположение практически всех тем .

Основное свойство дроби. Сокращение дробей. Практическая часть — решение задачи. 5 класс.

дроби #сокращениедробей #MEKTEП_OnLine #MEKTEP_OnLine МЕКТЕП OnLine — образовательный проект! Эльмира Рафикова — преподаватель .

Алгебра 8. Урок 2 — Сокращение дробей

Изучается сокращение рациональных дробей. Рассматриваются всевозможные случаи, связанные с разложением на множители и формулами .

Основное свойство дроби | Сокращение дробей

В этом видео разбирается основное свойство дроби, рассматриваются различные примеры на сокращение дробей Моя страница в Instagram с .

МАТЕМАТИКА-6, МЕРЗЛЯК. СОКРАЩЕНИЕ ДРОБЕЙ. ПАРАГРАФ-8

ТЕОРИЯ 00:00 ———— 07:13 РЕШАЕМ УСТНО 1-6 07:14 ———— 13:59 210-212 14:00 ———— 23:35 213-215 23:36 ———— 32:06 216-218 32:07 .

Как сокращать дроби ( Математика — 5 класс )

Сокращение обыкновенных дробей ================== Станьте спонсором канала (для тех, у кого есть желание и возможность), перейдя по ссылке: .

Сокращение дробей

Основное свойство дроби. Сокращение дробей. Несократимая дробь. Математика 5-6 классы. Урок 23. Поддержать Проект: .

Сокращение дробей. Математика 6 класс. Пример из учебника Макарычева. Тренировка

Ребята! Мы сегодня разбираем пример из учебника Макарычева для 6-го класса. Это про сокращение обыкновенных дробей. Вы иногда не знаете, .

6 класс, 10 урок, Приведение дробей к общему знаменателю

Решаем задачи(упражнения) на заказ (!). P.S. Если хочешь решать задачи и при этом зарабатывать, то напиши нам на whatsaap: +7(707)7328227 .

6 класс. Математика. Урок 11. «Сокращение дробей.»

6класс #математика #обыкновенныедроби #сложениеобыкновенныхдробей #сокращениедробей #основноесвойстводроби.

6 класс Урок №9. Сокращение дробей. Видео-уроки по математике учителя Елены Яковлевой

6 класс Урок №9. Сокращение дробей. Видео-уроки по математике учителя Елены Яковлевой полностью можно увидеть на сайте .

СОКРАЩЕНИЕ ДРОБЕЙ. Решение задач. Видеоурок | МАТЕМАТИКА 6 класс

На основе методов сокращения обыкновенных дробей и основного свойства дробей приводится решение нескольких заданий для закрепления знаний .

6 класс, 8 урок, Основное свойство дроби

Решаем задачи(упражнения) на заказ (!). P.S. Если хочешь решать задачи и при этом зарабатывать, то напиши нам на whatsaap: +7(707)7328227 .

Основное свойство дроби Сокращение дробей

Основное свойство дроби Сокращение дробей.

6 класс, 13 урок, Умножение дробей

Решаем задачи(упражнения) на заказ (!). P.S. Если хочешь решать задачи и при этом зарабатывать, то напиши нам на whatsaap: +7(707)7328227 .

Основное свойство дроби. Сокращение дробей

Основное свойство дроби. Сокращение дробей. В этом видео вы узнаете основное свойство дроби, а также научитесь как сокращать дроби.

2 Примеры Как сокращать дроби легко и правильно, несколько способов МАТЕМАТИКА ОНЛАЙН

НЕ ЗУБРИ МАТЕМАТИКУ. Лучше посмотри видео Поддержи меня: Сбербанк +79081662278 Репетитор по математике Нижний Новгород .

Источник

Сокращение дробей: правила и примеры

Разберемся в том, что такое сокращение дробей, зачем и как сокращать дроби, приведем правило сокращения дробей и примеры его использования.

Что такое «сокращение дробей»

Сократить дробь — значит разделить ее числитель и знаменатель на общий делитель, положительный и отличный от единицы.

В результате такого действия получится дробь с новым числителем и знаменателем, равная исходной дроби.

К примеру, возьмем обыкновенную дробь 6 24 и сократим ее. Разделим числитель и знаменатель на 2 , в результате чего получим 6 24 = 6 ÷ 2 24 ÷ 2 = 3 12 . В этом примере мы сократили исходную дробь на 2 .

Приведение дробей к несократимому виду

В предыдущем примере мы сократили дробь 6 24 на 2 , в результате чего получили дробь 3 12 . Нетрудно заметить, что эту дробь можно сократить еще. Как правило, целью сокращения дробей является получение в итоге несократимой дроби. Как привести дробь к несократимому виду?

Это можно сделать, если сократить числитель и знаменатель на их наибольший общий делитель (НОД). Тогда, по свойству наибольшего общего делителя, в числителе и в знаменателе будут взаимно простые числа, и дробь окажется несократимой.

a b = a ÷ Н О Д ( a , b ) b ÷ Н О Д ( a , b )

Приведение дроби к несократимому виду

Чтобы привести дробь к несократимому виду нужно ее числитель и знаменатель разделить на их НОД.

Вернемся к дроби 6 24 из первого примера и приведем ее к несократимому виду. Наибольший общий делитель чисел 6 и 24 равен 6 . Сократим дробь:

6 24 = 6 ÷ 6 24 ÷ 6 = 1 4

Сокращение дробей удобно применять, чтобы не работать с большими цифрами. Вообще, в математике существует негласное правило: если можно упростить какое-либо выражение, то нужно это делать. Под сокращением дроби чаще всего подразумевают ее приведение к несократимому виду, а не просто сокращение на общий делитель числителя и знаменателя.

Правило сокращения дробей

Чтобы сокращать дроби достаточно запомнить правило, которое состоит из двух шагов.

Правило сокращения дробей

Чтобы сократить дробь нужно:

1. Найти НОД числителя и знаменателя.
2. Разделить числитель и знаменатель на их НОД.

Рассмотрим практические примеры.

Пример 1. Сократим дробь.

Дана дробь 182 195 . Сократим ее.

Найдем НОД числителя и знаменателя. Для этого в данном случае удобнее всего воспользоваться алгоритмом Евклида.

195 = 182 · 1 + 13 182 = 13 · 14 Н О Д ( 182 , 195 ) = 13

Разделим числитель и знаменатель на 13 . Получим:

182 195 = 182 ÷ 13 195 ÷ 13 = 14 15

Готово. Мы получили несократимую дробь, которая равна исходной дроби.

Как еще можно сокращать дроби? В некоторых случаях удобно разложить числитель и знаменатель на простые множители, а потом из верхней и нижней частей дроби убрать все общие множители.

Пример 2. Сократим дробь

Дана дробь 360 2940 . Сократим ее.

Для этого представим исходную дробь в виде:

360 2940 = 2 · 2 · 2 · 3 · 3 · 5 2 · 2 · 3 · 5 · 7 · 7

Избавимся от общих множителей в числителе и знаменателе, в результате чего получим:

360 2940 = 2 · 2 · 2 · 3 · 3 · 5 2 · 2 · 3 · 5 · 7 · 7 = 2 · 3 7 · 7 = 6 49

Наконец, рассмотрим еще один способ сокращения дробей. Это так называемое последовательное сокращение. С использованием этого способа сокращение производится в несколько этапов, на каждом из которых дробь сокращается на какой-то очевидный общий делитель.

Пример 3. Сократим дробь

Сократим дробь 2000 4400 .

Сразу видно, что числитель и знаменатель имеют общий множитель 100 . Сокращаем дробь на 100 и получаем:

2000 4400 = 2000 ÷ 100 4400 ÷ 100 = 20 44

Далее замечаем, что числитель и знаменатель дроби 20 44 делятся на 2 . Сокращаем и приходим к виду:

20 44 = 20 ÷ 2 44 ÷ 2 = 10 22

Получившийся результат снова сокращаем на 2 и получаем уже несократимую дробь:

Источник

Сокращение обыкновенных дробей

О чем эта статья:

Что такое «сокращение дробей»

Математика любит точность и краткость: лохматыми громоздкими числами ее расположение не заслужить. Поэтому, следуя негласному правилу, сокращайте все, что можно сократить.

Сократить дробь — значит разделить ее числитель и знаменатель на их общий делитель. Общий делитель должен быть положительным и не равен нулю и единице.

В результате сокращения вы получаете новую дробь, равную исходной дроби. Такие дроби равны по основному свойству:

Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число — получится дробь, равная данной.

С основным свойством дроби знакомятся в 5 классе, но встречаться оно будет до самого окончания школы. Поэтому запоминаем, как выглядит основное свойство дроби в виде буквенных выражений:

=

=

где a, b, m — натуральные числа.

Графически сокращение дробей обычно записывается вот так:

Числитель и знаменатель зачеркиваются черточками. В этом примере числитель — 8, знаменатель — 36. Справа над ними записывают результаты деления числителя и знаменателя на их общий делитель. Общий делить 8 и 36 — 4. Это число не нужно записывать.

Пример 1. Сократим обыкновенную дробь

Разделим числитель и знаменатель на общий делитель 3.

= =

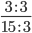
Сокращение выполнено: =

Пример 2. Сократим обыкновенную дробь

Разделим числитель и знаменатель на общий делитель 2.

= =

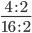
Сокращение выполнено: =

Приведение дробей к несократимому виду

Смысл сокращения дробей в том, чтобы в результате сокращения в числителе и знаменателе оказались наименьшие из возможных чисел.

Так, в результате сокращения в примере 2, мы из дроби получили дробь

Выходит, что дробь выдержит еще одно сокращение и придет к виду

Сокращая дробь, стремитесь в итоге получить несократимую дробь.

Разделите числитель и знаменатель дроби на их НОД (наибольший общий делитель). Так вы приведете дробь к несократимому виду.

— несократимая дробь, так как по свойствам НОД мы знаем, что:

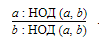
a : НОД(a, b) и b : НОД(a, b) — взаимно простые числа.

Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице, НОД(a, b) = 1.

• Несократимые дроби: ; ; ;

Пример 3. Приведите обыкновенную дробь к несократимому виду

Найдем НОД числителя и знаменателя. НОД = 12

Найдем частное: 12 : 12 = 1

= =

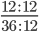
Сокращение выполнено: =

Пример 4. Приведите обыкновенную дробь к несократимому виду

Найдем НОД числителя и знаменателя. НОД = 5

Найдем частное: 15 : 5 = 3

= =

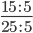
Сокращение выполнено: =

Правило сокращения дробей

Чтобы без труда сокращать любую обыкновенную дробь, запомните правило.

Выполняйте сокращение дробей по следующему алгоритму:

1. Найдите НОД числителя и знаменателя дроби.
2. Разделите числитель и знаменатель дроби на НОД.

В 6 классе каждая вторая задачка — с дробями. Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей.

Чтобы легко сокращать дроби, нужно уметь быстро находить НОД числителя и знаменателя. Для этого неплохо бы знать таблицу умножения и уметь раскладывать числа на простые множители.

• Например, дана дробь

Чтобы найти НОД числителя и знаменателя, разложим числа на простые множители.
36 = 2 * 2 * 3 * 3
84 = 2 * 2 * 3 * 7

Перемножаем все общие множители между собой 2 * 2 * 3 = 12.
НОД 36 и 84 = 12.

Пример 5. Сократите дробь

Разложим числа в числителе и знаменателе на множители.
135 = 9 * 3 * 5
180 = 9 * 2 * 2 * 5

Мысленно убираем все общие множители и перемножаем оставшиеся.

= =

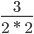
Сокращение выполнено: =

Пример 6. Сократите обыкновенную дробь

Найдем НОД числителя и знаменателя. НОД = 9

= =

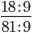
Сокращение выполнено: =

Дробь можно сократить, последовательно сокращая числитель и знаменатель на общий делитель. Такой способ подходит, если в числителе и знаменателе стоят крупные числа, и вы не уверены в подобранном НОД.

Пример 6. Сократите дробь:

= = =

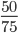
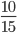
Сокращение выполнено: =

Пример 7. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

168 = 2 * 2 * 2 * 3 * 7

240 = 2 * 2 * 2 * 2 * 3 * 5

Перемножаем все общие множители между собой 2 * 2 * 2 * 3 = 24

НОД 168 и 240 равен 24

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 168 : 24 = 7

= =

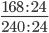
Сокращение выполнено: =

Пример 8. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

360 = 2 * 2 * 2 * 3 * 3 * 5

540 = 2 * 2 * 3 * 3 * 3 * 5

Перемножаем все общие множители между собой 2 * 2 * 3 * 3 * 5 = 180

НОД 360 и 540 равен 180

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 360 : 180 = 2

= =

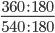
Сокращение выполнено: =

Пример 8. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

420 = 2 * 2 * 3 * 5 * 7

2520 = 2 * 2 * 2 * 3 * 3 * 5 * 7

Перемножаем все общие множители между собой 2 * 2 * 3 * 5 * 7 = 420

НОД 420 и 2520 равен 420

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 420 : 420 = 1

= =

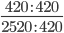
Сокращение выполнено. Дробь приведена к несократимому виду: =

Пример 9. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

1575 = 3 * 3 * 5 * 5 * 7

3450 = 2 * 3 * 5 * 5 * 23

Перемножаем все общие множители между собой 3 * 5 * 5 = 75

НОД 1575 и 3450 равен 72

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 1575 : 75 = 21

= =

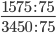
Сокращение выполнено. Дробь приведена к несократимому виду: =

Иногда разложение на простые множители занимает немало времени, особенно если раскладываемые числа большие, как в двух предыдущих примерах. Чтобы быстро разложить любое число на простые множители, можно обратиться к онлайн-калькулятору — в интернете их много. Воспользуйтесь одним из них.

Если времени совсем не хватает — можно использовать онлайн-калькулятор и для нахождения НОД. Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами.

Источник
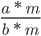
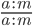
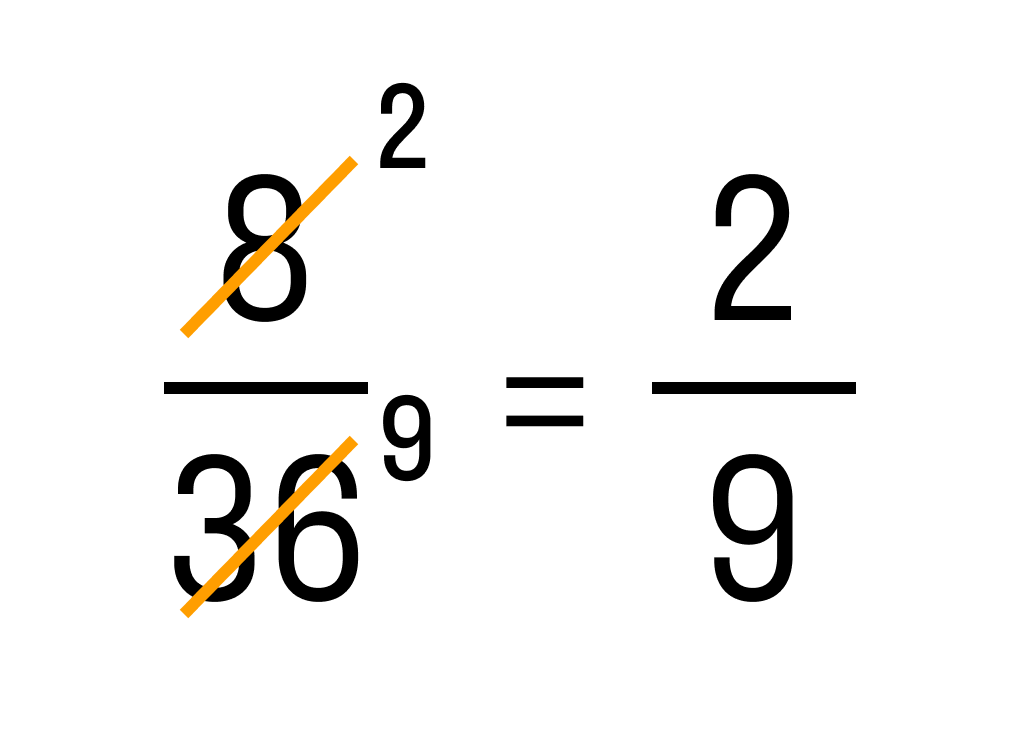
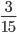
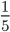
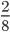
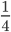
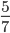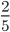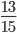