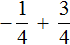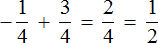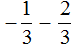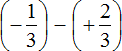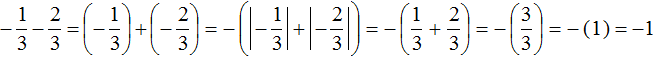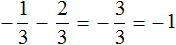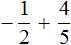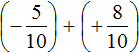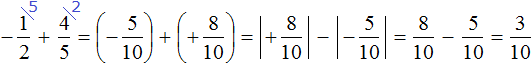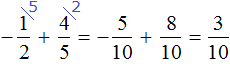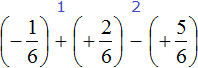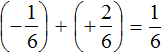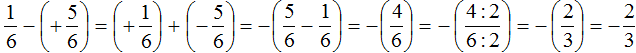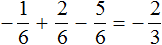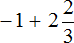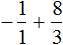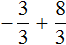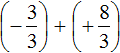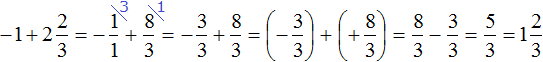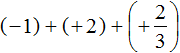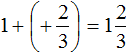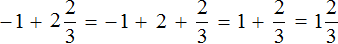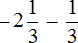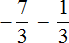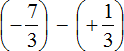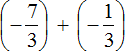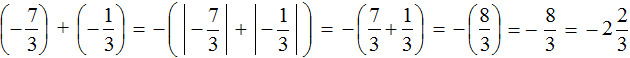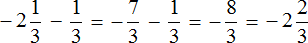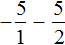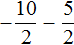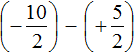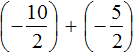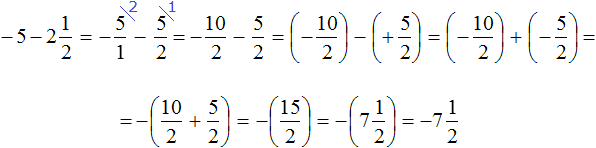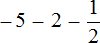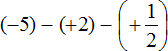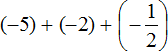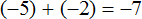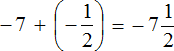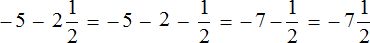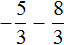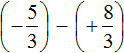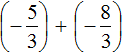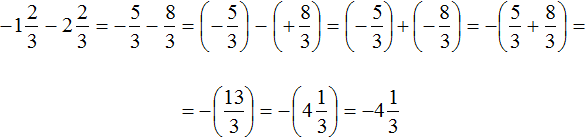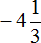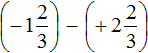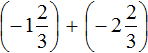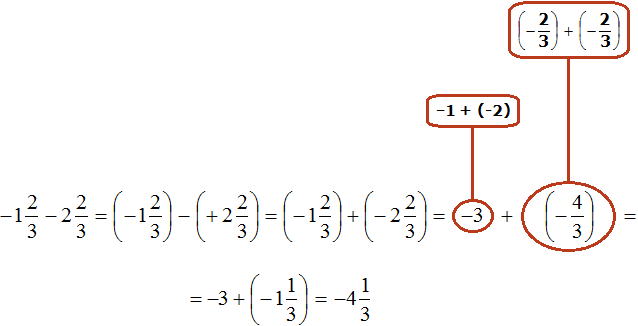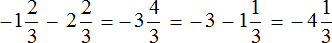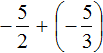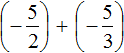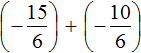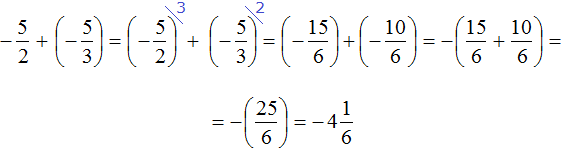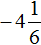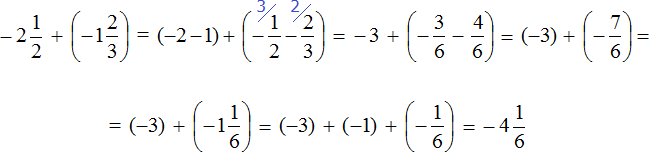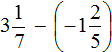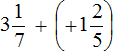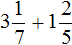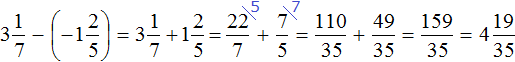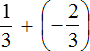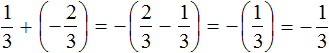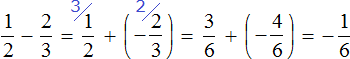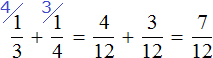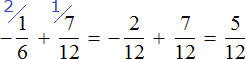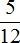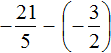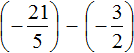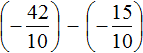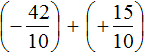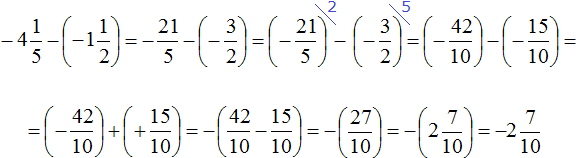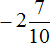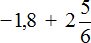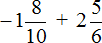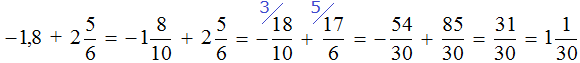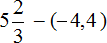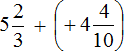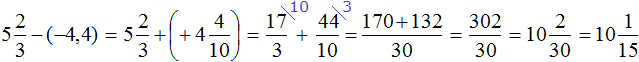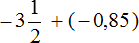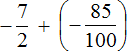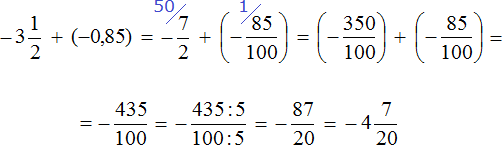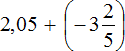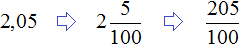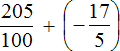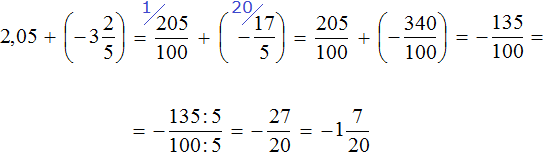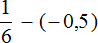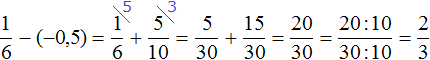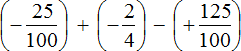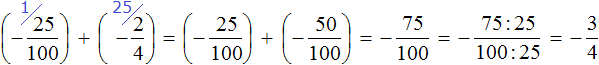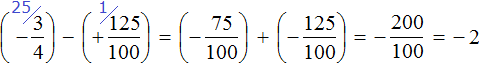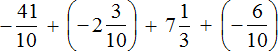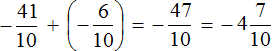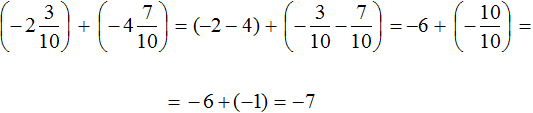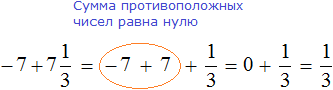Способ сложения рациональных чисел

Действия с рациональными числами

Сложение

При сложении двух рациональных чисел с одинаковым знаком складываются их модули и перед суммой ставится их общий знак.

Пример 1. Найти сумму рациональных чисел 2,5 и 3,2.

Решение: Так как модуль положительного числа равен самому числу, то в данном примере числа можно просто сложить:

Пример 2. Найти сумму отрицательных чисел (-2,5) и (-3,2).

Решение: Сначала надо сложить модули слагаемых:

Так как сумма двух отрицательных чисел должна быть отрицательным числом, то решение будет выглядеть так:

Из данных примеров следует, что в результате сложения двух положительных чисел получится положительное число, а в результате сложения двух отрицательных чисел – отрицательное число.

При сложении двух рациональных чисел с разными знаками нужно взять их модули и из большего вычесть меньший. В результате ставится знак того числа, у которого модуль больше.

Другими словами, можно просто, не обращая внимания на знаки, вычесть из большего числа меньшее и у получившегося результата поставить знак большего числа:

(-4,7) + (+12) = 7,3, так как 12 — 4,7 = 7,3;

9 + (-15) = -6, так как 15 — 9 = 6.

Из данных примеров следует, что в результате сложения двух чисел с разными знаками, может получится как положительное, так и отрицательное число.

Вычитание

Вычитание одного рационального числа из другого можно заменить сложением. При этом уменьшаемое берётся со своим знаком, а вычитаемое – с противоположным.

(+10) — (-3,4) = (+10) + (+3,4) = 13,4;

Из данных примеров следует, что чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.

Умножение

При умножении двух рациональных чисел умножаются их модули. Перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные.

Ниже представлена схема (правило знаков при умножении):

Из данных примеров следует, что в результате умножения двух чисел с разными знаками получится отрицательное число, а результате умножения двух чисел с одинаковыми знаками – положительное.

При умножении любого числа на -1 получится число, противоположное данному.

Деление

При делении одного рационального числа на другое делят модуль первого числа на модуль второго. Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные.

При делении используется то же правило, что и для умножения. Ниже представлена схема (правило знаков при делении):

Из данных примеров следует, что частное двух чисел с разными знаками – отрицательное число, а частное двух чисел с одинаковыми знаками – положительное число.

При делении любого числа на -1 получится число, противоположное данному.

Источник

Сложение рациональных чисел

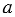
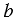
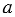
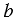
Если к числу прибавить положительное число , то точка с координатой переместится по координатной прямой на единичных отрезков вправо.

Примеры:

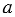
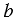
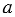
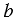
Если к числу прибавить отрицательное число , то точка с координатой переместится по координатной прямой на единичных отрезков влево.

Примеры:

Обратите внимание: любое число от прибавления положительного числа увеличивается, а от прибавления отрицательного числа уменьшается.

На основе примеров 4 + 3 = 1, 2,5 + 4 = 1,5 и 5 + (3) = 2 можно сделать следующий вывод:

Чтобы сложить два числа с разными знаками, надо:

1) найти модули слагаемых;

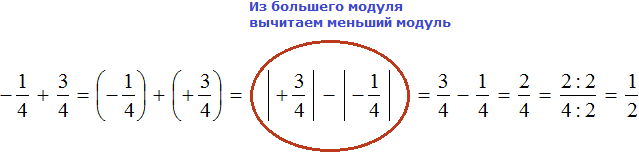
2) из большего модуля вычесть меньший модуль;

3) перед полученным числом поставить знак слагаемого с большим модулем.

На основе примера 2,5 + (2) = 4,5 можно сделать следующий вывод:

Чтобы сложить два отрицательных числа, надо:

1) найти модули слагаемых;

2) сложить модули слагаемых;

3) перед полученным числом поставить знак ««.

На основе примера 5 + 5 = 0 и 5 + (5) = 0 можно сделать следующий вывод:

Сумма двух противоположных чисел равна нулю, можно записать так: .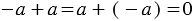

Также справедливо следующее правило:

Если 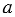— рациональное число, то .

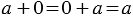Примеры:

1) 5 + 0 = 0 + 5 = 5;

2) 3 + 0 = 0 + (3) = 3.

Поделись с друзьями в социальных сетях:

Источник

Сложение рациональных чисел, правила и примеры.

Сложение рациональных чисел происходит по правилам сложения дробей. В этой теме рассмотрим подробно как складывать положительные и отрицательные рациональные числа, а также рациональные числа с одинаковыми и разными знаменателями.

Тема. Сложение рациональных чисел с одинаковыми знаменателями.

Определение:
Сумма дробей с одинаковыми положительными знаменателями, есть дробь с тем же знаменателем и суммой их числителей.

Правила сложения рациональных чисел.

1. Если у дробей одинаковый знаменатель, записываем его в знаменатель итоговой дроби.
2. Числители складываем по правилам сложения и результат записываем в числитель итоговой дроби.
3. Если требуется итоговую дробь сокращаем и преобразовываем.

Пример:
Выполните сложение рациональных чисел с одинаковыми знаменателями: а) \(\frac<-3><4>+\frac<1><4>\) б) \(\frac<-6><13>+\frac<-2><13>\) в) \(\frac<17><47>+\frac<12><47>\) г) \(\frac<32><15>+\frac<-12><15>\)

Решение:
а) Так как знаменатели у дробей одинаковые, записываем знаменатель тот же. Числители складываем по правилу сложения целых чисел. Итоговую дробь \(\frac<-2><4>\) сокращаем на 2.

Урок. Сложение рациональных чисел с разными знаменателями.

Определение:
Чтобы сложить две дроби с разными знаменателями необходимо сначала найти общий знаменатель, а потом сложить их числители.

Формула сложение рациональных чисел с разными знаменателями:

Алгоритм действия при сложении рациональных чисел с разными знаменателями.

1. Найти общий знаменатель. (Как находить общий знаменатель можете узнать, нажав на ссылку)
2. Найти сумму дробей по правилам сложения рациональных чисел с одинаковыми знаменателями.

Пример:
Выполните сложение рациональных чисел с разными знаменателями: а) \(\frac<-4><7>+\frac<5><8>\) б) \(\frac<-3><11>+\frac<-7><22>\) в) \(\frac<11><15>+\frac<9><25>\) г) \(\frac<8><3>+\frac<-1><13>\)

Решение:
а) Дроби \(\frac<-4><7>+\frac<5><8>\) имеют разные знаменатели, поэтому нужно найти общий знаменатель. Общий знаменатель будет равен 56, поэтому первую дробь \(\frac<-4><7>\) умножаем на 8, а вторую дробь \(\frac<5><8>\) на 7

б) Так как у дробей разные знаменатели, находим общий знаменатель. Общий знаменатель равен 22.

в) У дробей \(\frac<11><15>\) и \(\frac<9><25>\) разные знаменатели. Находим общий знаменатель, он равен 75. Первую дробь умножаем на 5, а вторую дробь умножаем на 3.

г) Общий знаменатель этих дробей \(\frac<8><3>\) и \(\frac<-1><13>\) равен 39.

Сложение противоположных рациональных чисел.

Правило сложения противоположных рациональных чисел.
Результатом сложения противоположных рациональных чисел будет нуль.

Пример:
Выполните сложение дробей \(\frac<-5><18>+\frac<5><18>\) .

Сложение положительных рациональных чисел.

Сложение положительных рациональных чисел сводится к сложение обыкновенных дробей. Может быть два варианта:

1. Если у положительных рациональных чисел разные знаменатели, то ищем общий знаменатель.
2. Если у положительных рациональных чисел одинаковые знаменатели, то переходим к сложению числителей, а знаменатель переписываем.

Примеры:
Выполните сложение положительных рациональных дробей: а) \(\frac<4><15>+\frac<7><15>\) б) \(\frac<3><8>+\frac<5><12>\).

б) У дробей разные знаменатели нужно найти общий знаменатель. Общий знаменатель равен 24.

Сложение отрицательных рациональных чисел.

Складываем отрицательные рациональные числа по этим правилам:

1. Если знаменатели разные, то приводим к общему знаменателю.
2. Если знаменатели одинаковые складываем числители по правилу сложения отрицательных целых чисел.

Пример:
Сложите отрицательные рациональные числа: а) \(-\frac<13><19>+(-\frac<1><19>)\) б) \(-\frac<1><49>+(-\frac<5><14>)\).

б) Для начала найдем общий знаменатель. Общий знаменатель у дробей равен 98.

Сложение рациональных чисел с разными знаками, примеры.

1. Если у дробей разные знаменатели, нужно привести их к общему знаменателю.
2. Если у дробей одинаковые знаменатели, нужно в итоговую дробь переписать знаменатель, а числители сложить по правилам сложения целых чисел с разными знаками.

Пример:
Выполните сложение рациональных чисел с разными знаками: а) \(-\frac<2><5>+\frac<1><5>\) б) \(\frac<1><27>+(-\frac<5><9>)\)

Решение:
а) У дробей общий знаменатель, переходим к сложению числителей. Определим какой знак будет в результате. Для этого посмотри модуль какого числа больше |-2|=2 и |1|=1. Получаем 2>1, то есть модуль отрицательного числа больше модуля положительного, поэтому в ответе будет стоять знак минус. Если сказать проще, у нас два минуса и один плюс. Минусов больше поэтому в результате поставим знак минус.

б) Сначала приведем к общему знаменателю, он равен 27, а потом сложим числители. Определим знак ответа. Найдем модули чисел |-15|=15 и |1|=1. Модуль отрицательного числа больше положительного 15>1, поэтому в ответе будет знак минус.

Источник

Сложение и вычитание рациональных чисел

В данном уроке рассматривается сложение и вычитание рациональных чисел. Тема относится к категории сложных. Здесь необходимо использовать весь арсенал полученных ранее знаний.

Правила сложения и вычитания целых чисел справедливы и для рациональных чисел. Напомним, что рациональными называют числа, которые могут быть представлены в виде дроби , где a – это числитель дроби, b – знаменатель дроби. При этом, b не должно быть нулём.

В данном уроке дроби и смешанные числа мы всё чаще будем называть одним общим словосочетанием — рациональные числа.

Пример 1. Найти значение выражения:

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к дроби . У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:

Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих дробей до их вычисления:

Модуль рационального числа больше, чем модуль рационального числа . Поэтому мы из вычли . Получили ответ . Затем сократив эту дробь на 2, получили окончательный ответ .

Некоторые примитивные действия, такие как заключение чисел в скобки и проставление модулей, можно пропустить. Данный пример вполне можно записать покороче:

Пример 2. Найти значение выражения:

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус, стоящий между рациональными числами 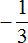и является знаком операции и не относится к дроби . У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:

Заменим вычитание сложением. Напомним, что для этого нужно к уменьшаемому прибавить число, противоположное вычитаемому:

Получили сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус:

Запишем решение данного примера покороче:

Примечание. Заключать в скобки каждое рациональное число вовсе необязательно. Делается это для удобства, чтобы хорошо видеть какие знаки имеют рациональные числа.

Пример 3. Найти значение выражения:

В этом выражении у дробей разные знаменатели. Чтобы облегчить себе задачу, приведём эти дроби к общему знаменателю. Не будем подробно останавливаться на том как это сделать. Если испытываете с этим затруднения, обязательно повторите урок действия с дробями.

После приведения дробей к общему знаменателю выражение примет следующий вид:

Заключим каждое рациональное число в скобки вместе своими знаками:

Это сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:

Запишем решение данного примера покороче:

Пример 4. Найти значение выражения

Заключим каждое рациональное число в скобки вместе со своими знаками:

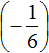
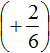
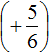
Вычислим данное выражение в следующем порядке: слóжим рациональные числа и , затем из полученного результата вычтем рациональное число .

Первое действие:

Второе действие:

Таким образом, значение выражения равно

Пример 5. Найти значение выражения:

Представим целое число −1 в виде дроби 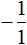, а смешанное число переведём в неправильную дробь:

Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Получили сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:

Есть и второй способ решения. Он заключается в том, чтобы сложить отдельно целые части.

Итак, вернёмся к изначальному выражению:

Заключим каждое число в скобки. Для этого смешанное число временно развернём:

Вычислим целые части:

В главном выражении вместо (−1) + (+2) запишем полученную единицу:

Полученное выражение 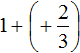свернём. Для этого запишем единицу и дробь вместе:

Запишем решение этим способом покороче:

Пример 6. Найти значение выражения

Переведём смешанное число 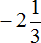в неправильную дробь. Остальную часть перепишем без изменения:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Заменим вычитание сложением:

Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:

Запишем решение данного примера покороче:

Пример 7. Найти значение выражение

Представим целое число −5 в виде дроби 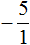, а смешанное число переведём в неправильную дробь:

Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Заменим вычитание сложением:

Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:

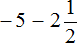
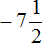
Таким образом, значение выражения равно .

Решим данный пример вторым способом. Вернемся к изначальному выражению:

Запишем смешанное число 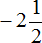в развёрнутом виде. Остальное перепишем без изменений:

Заключим каждое рациональное число в скобки вместе своими знаками:

Заменим вычитание сложением там, где это можно:

Вычислим целые части:

В главном выражении вместо 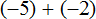запишем полученное число −7

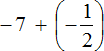
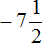
Выражение является развёрнутой формой записи смешанного числа . Запишем число −7 и дробь вместе, образуя окончательный ответ:

Запишем это решение покороче:

Пример 8. Найти значение выражения

Переведём смешанные числа в неправильные дроби:

Заключим каждое рациональное число в скобки вместе своими знаками:

Заменим вычитание сложением:

Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:

Таким образом, значение выражения равно

Данный пример можно решить и вторым способом. Он заключается в том, чтобы сложить целые и дробные части по отдельности. Вернёмся к изначальному выражению:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Заменим вычитание сложением:

Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус. Но в этот раз слóжим по отдельности целые части (−1 и −2), и дробные 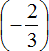и

Запишем это решение покороче:

Пример 9. Найти выражения выражения

Переведём смешанные числа в неправильные дроби:

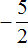
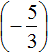
Заключим рациональное число в скобки вместе своим знаком. Рациональное число в скобки заключать не нужно, поскольку оно уже в скобках:

Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:

Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:

Таким образом, значение выражения 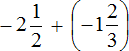равно

Теперь попробуем решить этот же пример вторым способом, а именно сложением целых и дробных частей по отдельности.

В этот раз, в целях получения короткого решения, попробуем пропустить некоторые действия, такие как: запись смешанного числа в развёрнутом виде и замена вычитания сложением:

Обратите внимание, что дробные части были приведены к общему знаменателю.

Пример 10. Найти значение выражения

Заменим вычитание сложением:

В получившемся выражении нет отрицательных чисел, которые являются основной причиной допущения ошибок. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вычитаемым, а также убрать скобки:

Получилось простейшее выражение, которое вычисляется легко. Вычислим его любым удобным для нас способом:

Пример 11. Найти значение выражения

Это сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:

Пример 12. Найти значение выражения

Выражение состоит из нескольких рациональных чисел. Согласно порядку действий, в первую очередь необходимо выполнить действия в скобках.

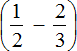
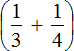
Сначала вычислим выражение , затем выражение Полученные результаты слóжим .

Первое действие:

Второе действие:

Третье действие:

Ответ: значение выражения 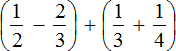равно

Пример 13. Найти значение выражения

Переведём смешанные числа в неправильные дроби:

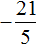
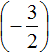
Заключим рациональное число в скобки вместе со своим знаком. Рациональное число заключать в скобки не нужно, поскольку оно уже в скобках:

Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:

Заменим вычитание сложением:

Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:

Таким образом, значение выражения 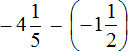равно

Рассмотрим сложение и вычитание десятичных дробей, которые тоже относятся к рациональным числам и которые могут быть как положительными, так и отрицательными.

Пример 14. Найти значение выражения −3,2 + 4,3

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к десятичной дроби 4,3. У этой десятичной дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы его запишем для наглядности:

Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих десятичных дробей до их вычисления:

Модуль числа 4,3 больше, чем модуль числа −3,2 поэтому мы из 4,3 вычли 3,2. Получили ответ 1,1. Ответ положителен, поскольку перед ответом должен стоять знак того рационального числа, модуль которого больше. А модуль числа 4,3 больше, чем модуль числа −3,2

Таким образом, значение выражения −3,2 + (+4,3) равно 1,1

Этот пример можно записать покороче:

Пример 15. Найти значение выражения 3,5 + (−8,3)

Это сложение рациональных чисел с разными знаками. Как и в прошлом примере из большего модуля вычитаем меньший и перед ответом ставим знак того рационального числа, модуль которого больше:

3,5 + (−8,3) = −(|−8,3| − |3,5|) = −(8,3 − 3,5) = −(4,8) = −4,8

Таким образом, значение выражения 3,5 + (−8,3) равно −4,8

Этот пример можно записать покороче:

Пример 16. Найти значение выражения −7,2 + (−3,11)

Это сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус.

Запись с модулями можно пропустить, чтобы не загромождать выражение:

−7,2 + (−3,11) = −7,20 + (−3,11) = −(7,20 + 3,11) = −(10,31) = −10,31

Таким образом, значение выражения −7,2 + (−3,11) равно −10,31

Этот пример можно записать покороче:

Пример 17. Найти значение выражения −0,48 + (−2,7)

Это сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:

−0,48 + (−2,7) = (−0,48) + (−2,70) = −(0,48 + 2,70) = −(3,18) = −3,18

Пример 18. Найти значение выражения −4,9 − 5,9

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус который располагается между рациональными числами −4,9 и 5,9 является знаком операции и не относится к числу 5,9. У этого рационального числа свой знак плюса, который невидим по причине того, что он не записывается. Но мы запишем его для наглядности:

Заменим вычитание сложением:

Получили сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:

(−4,9) + (−5,9) = −(4,9 + 5,9) = −(10,8) = −10,8

Таким образом, значение выражения −4,9 − 5,9 равно −10,8

Запишем решение этого примера покороче:

Пример 19. Найти значение выражения 7 − 9,3

Заключим в скобки каждое число вместе со своими знаками

Заменим вычитание сложением

Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:

(+7) + (−9,3) = −(9,3 − 7) = −(2,3) = −2,3

Таким образом, значение выражения 7 − 9,3 равно −2,3

Запишем решение этого примера покороче:

Пример 20. Найти значение выражения −0,25 − (−1,2)

Заменим вычитание сложением:

Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:

−0,25 + (+1,2) = 1,2 − 0,25 = 0,95

Запишем решение этого примера покороче:

Пример 21. Найти значение выражения −3,5 + (4,1 − 7,1)

Выполним действия в скобках, затем слóжим полученный ответ с числом −3,5

Первое действие:

4,1 − 7,1 = (+4,1) − (+7,1) = (+4,1) + (−7,1) = −(7,1 − 4,1) = −(3,0) = −3,0

Второе действие:

−3,5 + (−3,0) = −(3,5 + 3,0) = −(6,5) = −6,5

Ответ: значение выражения −3,5 + (4,1 − 7,1) равно −6,5.

Пример 22. Найти значение выражения (3,5 − 2,9) − (3,7 − 9,1)

Выполним действия в скобках. Затем из числа, которое получилось в результате выполнения первых скобок, вычтем число, которое получилось в результате выполнения вторых скобок:

Первое действие:

3,5 − 2,9 = (+3,5) − (+2,9) = (+3,5) + (−2,9) = 3,5 − 2,9 = 0,6

Второе действие:

3,7 − 9,1 = (+3,7) − (+9,1) = (+3,7) + (−9,1) = −(9,1 − 3,7) = −(5,4) = −5,4

Третье действие

0,6 − (−5,4) = (+0,6) + (+5,4) = 0,6 + 5,4 = 6,0 = 6

Ответ: значение выражения (3,5 − 2,9) − (3,7 − 9,1) равно 6.

Пример 23. Найти значение выражения −3,8 + 17,15 − 6,2 − 6,15

Заключим в скобки каждое рациональное число вместе со своими знаками

Заменим вычитание сложением там, где это можно:

Выражение состоит из нескольких слагаемых. Согласно сочетательному закону сложения, если выражение состоит из нескольких слагаемых, то сумма не будет зависеть от порядка действий. Это значит, что слагаемые можно складывать в любом порядке.

Не будем изобретать велосипед, а слóжим все слагаемые слева направо в порядке их следования:

Первое действие:

(−3,8) + (+17,15) = 17,15 − 3,80 = 13,35

Второе действие:

13,35 + (−6,2) = 13,35 − −6,20 = 7,15

Третье действие:

7,15 + (−6,15) = 7,15 − 6,15 = 1,00 = 1

Ответ: значение выражения −3,8 + 17,15 − 6,2 − 6,15 равно 1.

Пример 24. Найти значение выражения

Переведём десятичную дробь −1,8 в смешанное число. Остальное перепишем без изменения:

Далее вычисляем данное выражение, применяя ранее изученные правила:

Пример 25. Найти значение выражения

Заменим вычитание сложением. Попутно переведём десятичную дробь (−4,4) в неправильную дробь

В получившемся выражении нет отрицательных чисел. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вторым числом, и убрать скобки. Тогда получим простое выражение на сложение, которое решается легко

Пример 26. Найти значение выражения

Переведём смешанное число 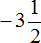в неправильную дробь, а десятичную дробь −0,85 в обыкновенную дробь. Получим следующее выражение:

Получили сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:

Пример 27. Найти значение выражения

Переведём обе дроби в неправильные дроби. Чтобы перевести десятичную дробь 2,05 в неправильную дробь, можно перевести ее сначала в смешанное число, а затем в неправильную дробь:

После перевода обеих дробей в неправильные дроби, получим следующее выражение:

Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль и перед полученным ответом поставим знак того числа, модуль которого больше:

Пример 28. Найти значение выражения

Заменим вычитание сложением. Далее переведём десятичную дробь в обыкновенную дробь. Затем вычислим получившееся выражение, применяя ранее изученные правила:

Пример 29. Найти значение выражения

Переведём десятичные дроби −0,25 и −1,25 в обыкновенные дроби, остальное перепишем без изменения. Получим следующее выражение:

Можно сначала заменить вычитание сложением там, где это можно и сложить рациональные числа одно за другим.

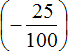
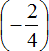
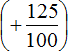
Есть и второй вариант: сначала сложить рациональные числа и , а затем из полученного результата вычесть . Этим вариантом и воспользуемся.

Первое действие:

Второе действие:

Ответ: значение выражения 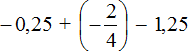равно −2.

Пример 30. Найти значение выражения

Переведём десятичные дроби в обыкновенные. Остальное перепишем без изменения:

Получили сумму из нескольких слагаемых. Если сумма состоит из нескольких слагаемых, то выражение можно вычислять в любом порядке. Это следует из сочетательного закона сложения.

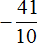
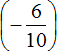
Поэтому мы можем организовать наиболее удобный для нас вариант. В первую очередь можно сложить первое и последнее слагаемое, а именно рациональные числа и . У этих чисел одинаковые знаменатели, а значит это освободит нас от необходимости приводить их к нему.

Первое действие:

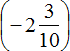
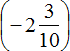
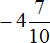
Полученное число можно сложить со вторым слагаемым, а именно с рациональным числом . У рациональных чисел и одинаковые знаменатели в дробных частях, что опять же является преимуществом для нас

Второе действие:

Ну и слóжим полученное число −7 с последним слагаемым, а именно с рациональным числом 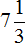. Удобно то, что при вычислении данного выражения, семёрки исчезнут, поскольку их сумма будет равна нулю:

Третье действие:

Ответ: значение выражения 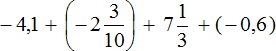равно

Источник