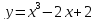- Методы графического сложения, вычитания
- Методы графического умножения, деления
- Сложение графиков функций
- 1. Введение
- 2. Основная часть «Сложение графиков функций»
- «Сложение и вычитание графиков» Из опыта работы учителя математики Першотравенской средней общеобразовательной школы I-III ступеней 2 Ильиной Н.В. Факультативное. — презентация
- Похожие презентации
- Презентация по предмету «Математика» на тему: ««Сложение и вычитание графиков» Из опыта работы учителя математики Першотравенской средней общеобразовательной школы I-III ступеней 2 Ильиной Н.В. Факультативное.». Скачать бесплатно и без регистрации. — Транскрипт:
- Сложение графиков функций
- Просмотр содержимого документа «Сложение графиков функций»
Методы графического сложения, вычитания
Чтобы построить график функции , надо построить на одном чертеже графики и , потом при каждом x сложить ординаты двух графиков.
Если необходимо построить график разности двух функций , то этот случай сводится к построению суммы: . Причем, график функции получается из графика функции симметричным отражением относительно оси .
В случае, когда вторая функция — константа, то графическое сложение означает сдвиг графика первой функции по вертикали на эту константу, причем, если константа положительная, то сдвиг осуществляется вверх, а если отрицательная, то вниз.
 |  |
Сложение двух функций: 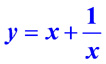 | Вычитание двух функций:  |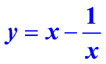
 |  |
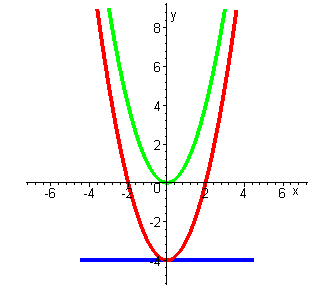Сложение функции и константы:  | Вычитание функции и константы:  |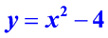
Методы графического умножения, деления
Чтобы построить график функции y=f(x)·g(x) , надо построить на одном чертеже графики y=f(x) и y=g(x) , потом при каждом x перемножить ординаты двух графиков.
Графическое деление выполняется аналогично произведению.
В частном случае при построении графика функции y=A·f(x) , где A — константа надо график функции y=f(x) растянуть в |A| раз по вертикали, при условии |A|≥1 , или сжать в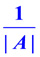 
раз по вертикали, если |A| , и затем полученный график отобразить симметрично относительно оси OX , если A .
В данном параграфе рассмотрены следующие примеры:
Источник
Сложение графиков функций
2. Основная часть «Сложение графиков функций». 4
3. Заключение. 13
1. Введение
На уроках алгебры мы научились строить графики элементарных функций: линейных, квадратичных, обратно пропорциональной зависимости, логарифмической, показательной, степенной, тригонометрических функций. В 9м и 10м классах мы научились строить многие графики способом геометрических преобразований графиков функций параллельного переноса, сдвиг вдоль оси координат, сжатие и растяжение вдоль координатных осей. Среди таких преобразований я выделила построение графиков способом сложения. Действительно, многие функции можно представить в виде суммы нескольких функций:
можно представить в виде суммы двух функций
функцию 
можно представить в виде суммы функций у(х)=х+2 и 
, график каждой функции мы умеем строить. Тогда возникает проблема: как построить график функции, который будет являться суммой двух функций. И так: цель моего реферата узнать правила построения графиков функций y=f(x), где f(x)=q(x)+h(x). Для этого мне надо получить необходимую информацию о таких графиках.
1. Изучить информацию по рассматриваемому вопросу в литературе, в том числе и в учебнике.
2. Выполнить практическое построение графиков функций, которые представляют собой сумму двух элементарных функций.
Теоретический материал по данному вопросу «Сложение графиков функций» я изучила по книгам: «Геометрические преобразования графиков функций» и «Графики функций» Справочник , , и другие. Из этих книг я узнала правила построения графиков методом сложения.
2. Основная часть «Сложение графиков функций»
На основании изученного материала, я пришла к выводу, что общий метод построения графиков суммы двух функций заключается в том, что предварительно строят два графика для обеих функций, а затем складывают ординаты этих кривых при одних и тех же значениях х (удобно — в характерных точках). По полученным точкам строят искомый график и выполняют проверку в нескольких контрольных точках.
В отдельных случаях построение графиков суммы функций можно выполнять так.
Если надо построить график суммы двух функций, то строят вначале график одной, более простой, функции, затем к нему пристраивают график второй функции, ординаты которого откладывают от соответствующих точек первого графика.
Построим график функции 
.
Строим графики функций-слагаемых 
и у = х. Затем складываем ординаты кривых при одинаковых значениях х. Возьмем значения х = , 1, 2, 3,….Складывая ординаты обоих графиков для каждого из этих значений х, получаем точки А, В, С, D. Соединив их плавной линией, получим одну ветвь графика функции (при х > 0). Заметив, что функция нечетная и график ее симметричен относительно начала координат, строим вторую ветвь графика заданной функции (при х 0 и ниже него при х
Источник
«Сложение и вычитание графиков» Из опыта работы учителя математики Першотравенской средней общеобразовательной школы I-III ступеней 2 Ильиной Н.В. Факультативное. — презентация
Презентация была опубликована 8 лет назад пользователемГалина Вырошникова
Похожие презентации
Презентация по предмету «Математика» на тему: ««Сложение и вычитание графиков» Из опыта работы учителя математики Першотравенской средней общеобразовательной школы I-III ступеней 2 Ильиной Н.В. Факультативное.». Скачать бесплатно и без регистрации. — Транскрипт:
1 «Сложение и вычитание графиков» Из опыта работы учителя математики Першотравенской средней общеобразовательной школы I-III ступеней 2 Ильиной Н.В. Факультативное занятие :
2 Из 24 участников старших классов в школьной олимпиаде по математике график функции y = x+sin x: 1)построили – 3 человека, 2)пробовали, но не смогли выполнить задание – 17 человек, 3)даже не пытались — 4 человека. В итоге: Проблема:
3 Цель занятия – содействовать: усвоению учащимися способа «сложения» для построения графиков функций ; усвоению учащимися способа «сложения» для построения графиков функций ; развитию навыков работы с графиками; развитию навыков работы с графиками; воспитанию интереса к графическому заданию функции. воспитанию интереса к графическому заданию функции.
4 Удобно ли строить график функции y=x+sin(x) обычным способом? x01 y0 Попробуй заполнить таблицу
5 Графики можно складывать как числа! График функции y=x+sinx можно получить сложением графиков функций y=x и y=sinx. График функции y=x+sinx можно получить сложением графиков функций y=x и y=sinx. Так как ординаты обеих функций при х=0 равны 0, то первая точка искомого графика О(0;0).
6 На графике y=x и y=sinx возьмём соответственно точки А и В так, чтобы абсциссы их были равны. Точку на оси OX с той же абсцисой назовём С. Отложим от т. А вверх расстояние AD равное BC. (т.е. к ординате y=x прибавим y=sin x) Полученная точка D – точка искомого графика. D A B C
7 В характерных точках оси ОХ (x=, x=, x= ) проделаем ту же самую операцию. Получим: D A B C Соединяем полученные точки, получим график искомой функции. Соединяем полученные точки, получим график искомой функции.
9 Построение графика суммы двух функций : 1) строят графики двух функций слагаемых; 2) ординаты второго графика откладывают от соответствующих точек первого графика.
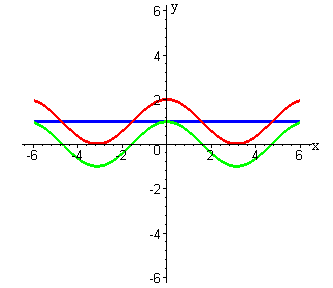
10 Попробуй свои силы на графике функции y=sin x + cos x.
11 Проверь себя ! C
12 Можно ли с помощью « сложения » построить график разности двух функций ? Например, Построим графики функций
13 Возьмём точки: О(0;0) принадлежащую и А(0;1) принадлежащую. От точки Отложим ординату точки А, взятую с противоположным знаком, т. е. -1. Получим точку В. B A
14 Аналогичную операцию проделаем в точках. Соединим точки и получим график искомой функции.
16 Построение графика разности двух функций : Построить графики функций; Построить графики функций; От графика функции уменьшаемого откладывают ординаты функции вычитаемого, взятые с противоположным знаком. От графика функции уменьшаемого откладывают ординаты функции вычитаемого, взятые с противоположным знаком.
17 Второй способ построения графика функции : Построить график функции и. Выполнить сложение графиков.
18 Заметим 1) при сложении и вычитании графиков можно пользоваться циркулем для сложения ординат 2) графики функции также можно строить с помощью умножения и деления
19 Умножение графиков Графики функции y=x и y=sin(x). Графики функции y=x и y=sin(x).
20 Произведение графиков y=x и y=sin(x) выглядит следующим образом :
21 Список использованной литературы 1) «Графики функций»; справочник; Вирченко Н. А., Ляшко И. И., Швецов К. И. – Киев: наук. думка, 1979 г. – 320 с. 2) «Функции и графики» Гельфанд И. М., Шноль Э. Э. – Москва: Наука, – 96 с. 3) «Алгебра и элементарные функции» Качетков Е. С., Качеткова Е. С. – Москва: Просвещение, 1966 – 285 с.
22 Также использовались Function Graphing Standart Edition 2.1 Microsoft PowerPoint (Office 2003) Paint Photoshop CS2 (Build 5021) Microsoft Equation 3.0
Источник
Сложение графиков функций
В разработке представлен способ сложения графиков функций и примеры с подробным объяснением.
Просмотр содержимого документа
«Сложение графиков функций»
Иногда функция, график которой должен быть построен, представляется как сумма двух или нескольких простейших функций. Графики простейших функций уже известны и без труда могут быть построены. В этом случае, рассмотрим способ сложения графиков.
Алгоритм. 1) Строим графики функций каждого слагаемого
2) Ординаты второго графика откладывают от соответствующих
ординат первого графика (можно пользоваться измерительным
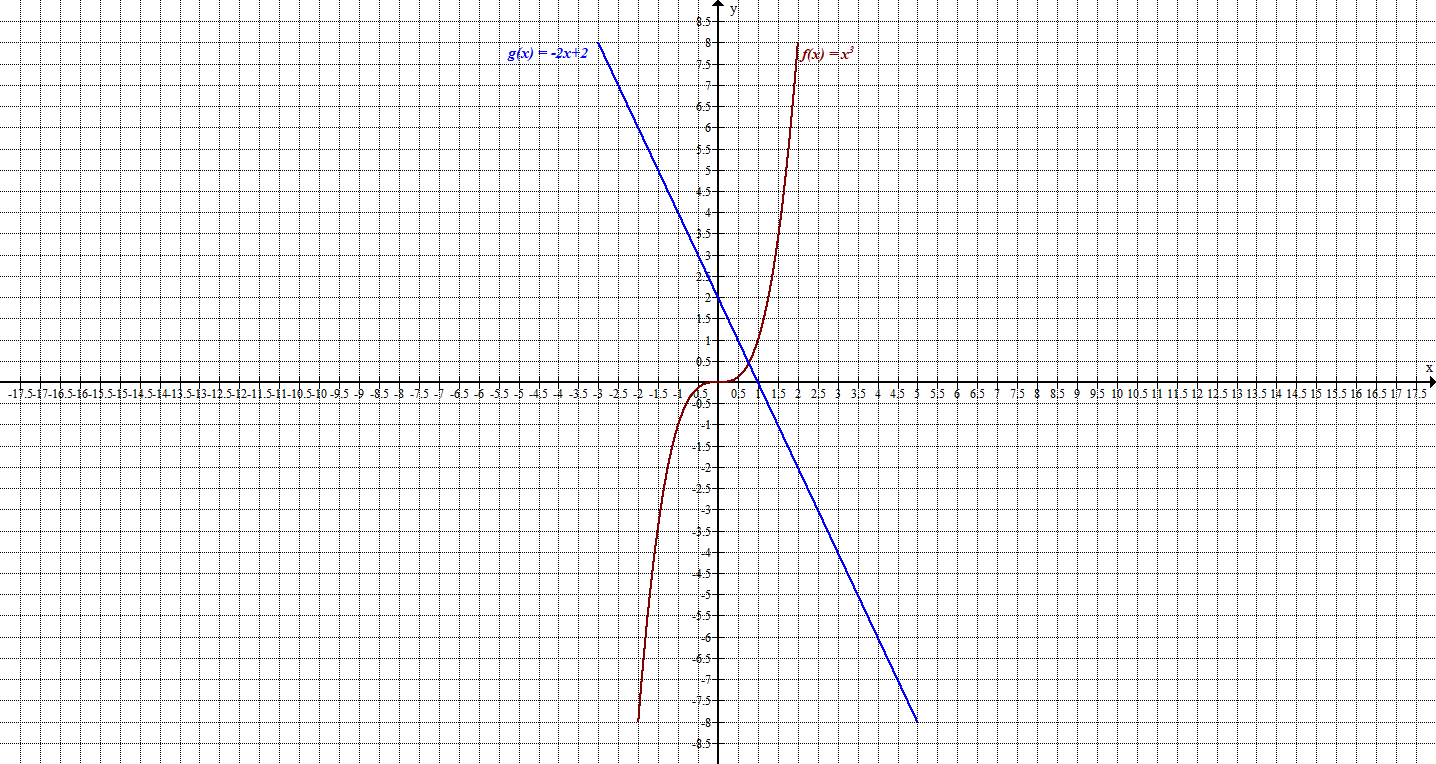
Пример 1. Построить график функции 
Представим эту функцию в виде суммы двух функций: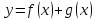 
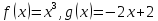
, где
. На одной системе координат строим графики этих функций.
Затем, каждую точку графика функции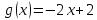 
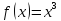
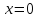
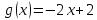
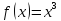
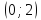
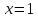
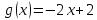
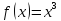
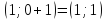
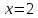
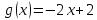
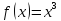
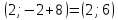
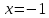
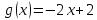
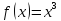
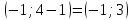
смещаем параллельно оси Оу на расстояние, равное ординате графика функции 
в соответствующей абсциссе. То есть, при 
ордината графика функции равна 2, а ордината графика функции равна 0, поэтому ставим точку 
. Далее, при 
ордината графика функции равна 0, а ордината графика функции равна 1, поэтому ставим точку 
. При 
ордината графика функции равна -2, а ордината графика функции равна 8, поэтому ставим точку 
. При 
ордината графика функции равна 4, а ордината графика функции равна -1, поэтому ставим точку 
. И так далее. Получаем график функции
Для того, чтобы график был как можно точнее, необходимо брать значимые точки, т.е. те, в которых происходит значимое событие для графика (пересечение с осями, точки перегиба, или точки, в которых график меняет своё направление).
Определим свойства функции
Значит, функция не является ни чётной, ни нечётной и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.
Точка пересечения с осью Оу:
Найдём точки экстремума:
Найдём экстремумы функции:
Функция возрастает при .
Функция убывает при .
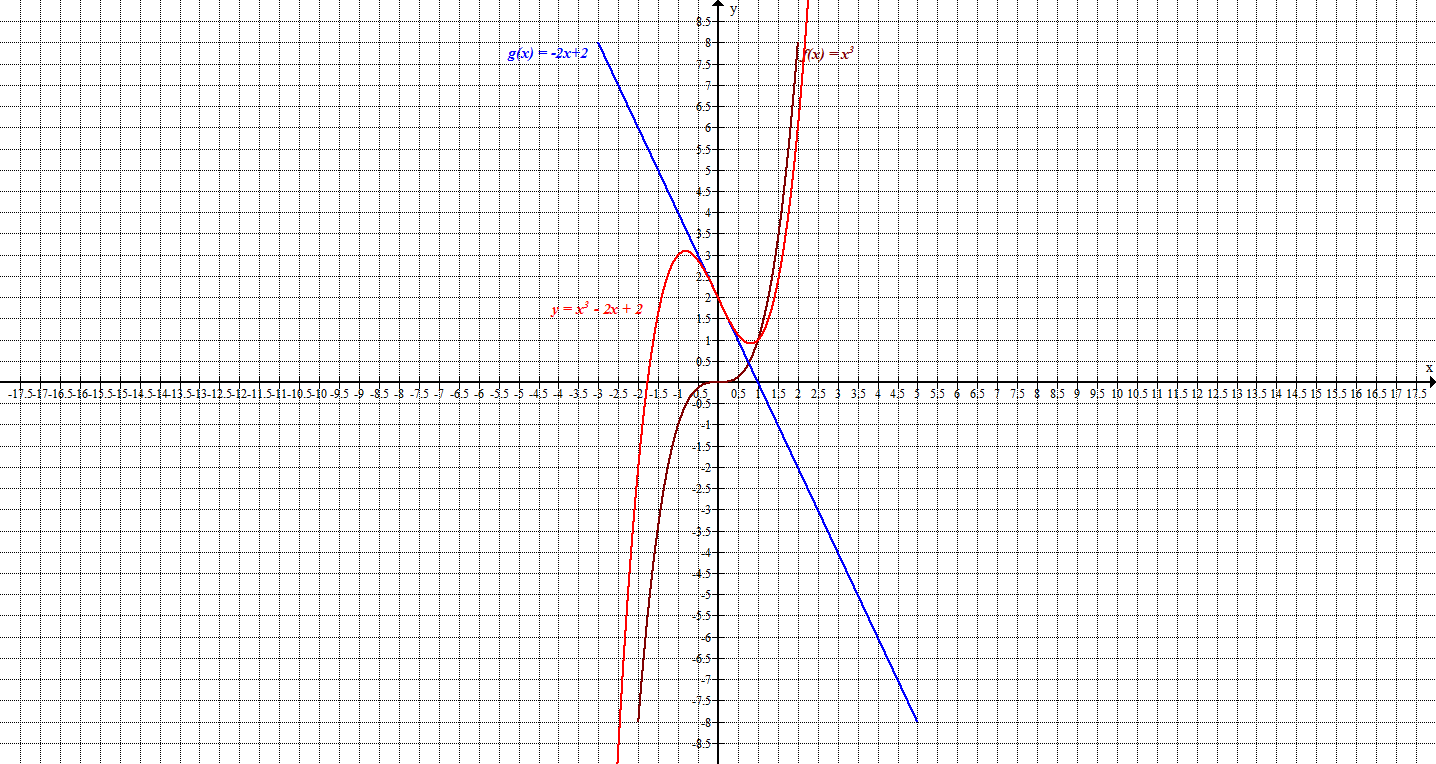
Пример 2. Построить график функции
Представим эту функцию в виде суммы двух функций: 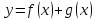, где
. На одной системе координат строим графики этих функций.
Производим аналогичные действия:
Получаем график функции .
Определим свойства функции
Значит, функция не является ни чётной, ни нечётной и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.
Точка пересечения с осью Оу:
Точки пересечения с осью Ох:
Значит, точки пересечения с осью Ох —
Найдём точки экстремума:
Найдём экстремумы функции:
Функция убывает при .Функция возрастает при .
Пример 3. Построить график функции
Представим эту функцию в виде суммы двух функций: 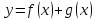, где
. На одной системе координат строим графики этих функций. Затем производим сложение.
Определим свойства функции
Чётность функции: Значит, функция является чётной, и её график симметричен относительно оси Оу.
Точка пересечения с осью Оу:
Точки пересечения с осью Ох:
Значит, точки пересечения с осью Ох —
Найдём точки экстремума:
Найдём экстремумы функции:
Функция возрастает при .
Функция убывает при .
Пример 4. Построить график функции
Представим эту функцию в виде суммы двух функций: 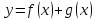, где
. На одной системе координат строим графики этих функций. Затем производим сложение.
Аналогичные вычисления для отрицательного аргумента. Получаем график функции
Определим свойства функции
Чётность функции: Значит, функция не является ни чётной, ни нечётной, и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.
Точка пересечения с осью Оу:
Точки пересечения с осью Ох:
. Значит, точки пересечения с осью Ох —
Найдём точки экстремума:
Найдём экстремумы функции:
Функция возрастает при .
Функция убывает при .
Особый случай представляется при сочетании обратной пропорциональности с каким-нибудь другим графиком. Приведём такой пример.
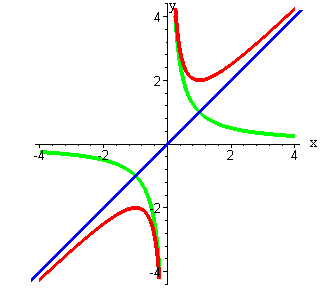
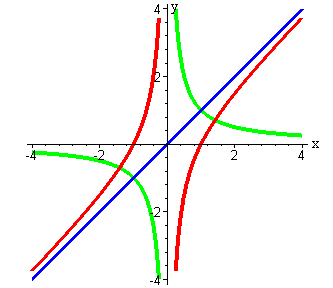
Пример 5. Построить график функции
Представим эту функцию в виде суммы двух функций: 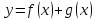, где
. На одной системе координат строим графики этих функций.
Что происходит? Так как график обратной пропорциональности не пересекает оси координат, то он и будет исходным. К его ординатам будем прибавлять ординаты графика функции .
График функции-суммы при значениях х, бесконечно близких к 0, практически сливается с графиком функции , располагаясь чуть выше его. А при очень больших значениях график функции-суммы почти сливается с графиком , располагаясь чуть выше его при положительных х, и чуть ниже при отрицательных х.
Определим свойства функции
Значит, функция не является ни чётной, ни нечётной, и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.
Точек пересечения с осью Оу нет.
Точки пересечения с осью Ох:
Значит, точка пересечения с осью Ох
Источник
