Способ сложения чисел от 1 до 100

Занимательная математика: правило Гаусса

Цикл «Занимательная математика» посвящен деткам увлекающимся математикой и родителям, которые уделяют время развитию своих детей, «подкидывая» им интересные и занимательные задачки, головоломки.

Первая статья из этого цикла посвящена правилу Гаусса.

Немного истории

Известный немецкий математик Карл Фридрих Гаусс (1777-1855) с раннего детства отличался от своих сверстников. Несмотря на то, что он был из небогатой семьи, он достаточно рано научился читать, писать, считать. В его биографии есть даже упоминание того, что в возрасте 4-5 лет он смог скорректировать ошибку в неверных подсчетах отца, просто наблюдая за ним.

Одно из первых его открытий было сделано в возрасте 6 лет на уроке математики. Учителю было необходимо увлечь детей на продолжительное время и он предложил следующую задачку:

Найти сумму всех натуральных чисел от 1 до 100.

Юный Гаусс справился с этим заданием достаточно быстро, найдя интересную закономерность, которая получила большое распространение и применяется по сей день при устном счете.

Давайте попробуем решить эту задачку устно. Но для начала возьмем числа от 1 до 10:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10

Посмотрите внимательно на эту сумму и попробуйте догадаться, что же необычного смог разглядеть Гаусс? Для ответа необходимо хорошо представлять себе состав чисел.

Гаусс сгруппировал числа следующим образом:

(1+10) + (2+9) + (3+8) + (4+7) + (5+6)

Таким образом маленький Карл получил 5 пар чисел, каждая из которых в отдельности в сумме дает 11. Тогда, чтобы вычислить сумму натуральных чисел от 1 до 10 необходимо

Вернемся к первоначальной задаче. Гаусс заметил, что перед суммированием необходимо группировать числа в пары и тем самым изобрел алгоритм, благодаря которому можно быстро сложить числа от 1 до100:

1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100

Находим количество пар в ряде натуральных чисел. В данном случае их 50.

Суммируем первое и последнее числа данного ряда. В нашем примере — это 1 и 100. Получаем 101.

Умножаем полученную сумму первого и последнего члена ряда на количество пар этого ряда. Получаем 101 * 50 = 5050

Следовательно, сумма натуральных чисел от 1 до 100 равна 5050.

Задачи на использование правила Гаусса

А сейчас вашему вниманию предлагаются задачи, в которых в той или иной степени используется правило Гаусса. Эти задачки вполне способен понять и решить четвероклассник.

Можно дать возможность ребенку порассуждать самому, чтобы он сам «изобрел» это правило. А можно разобрать вместе и посмотреть как он сможет его применить. Среди ниже приведенных задач есть примеры, в которых нужно понять как модифицировать правило Гаусса, чтобы его применить к данной последовательности.

В любом случае, чтобы ребенок мог оперировать этим в своих вычислениях необходимо понимание алгоритма Гаусса, то есть умение разбить правильно по парам и посчитать.

Важно! Если будет заучена формула без понимания, то это очень быстро будет забыто.

Задача 1

Найти сумму чисел:

• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
• 1 + 2 + 3 + … + 14 + 15 + 16;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9;
• 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100.

Вначале можно дать возможность ребенку самому решить первый пример и предложить найти способ, при котором это сделать легко в уме. Далее разобрать этот пример вместе с ребенком и показать как это сделал Гаусс. Лучше всего для наглядности записать ряд и соединить линиями пары чисел, дающие в сумме одинаковое число. Важно, чтобы ребенок понял как образуются пары — берем самое маленькое и самое большое из оставшихся чисел при условии, что количество чисел в ряду четно.

• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = (1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = (1 + 10) * 5;
• 1 + 2 + 3 + … + 14 + 15 + 16 = (1 + 16) + (2 + 15) + (3 + 14) + (4 + 13) + (5 + 12) + (6 + 11) + (7 + 10) + (8 + 9) = (1 + 16) * 8 = 136;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) + (2 + 7) + (3 + 6) + (4 + 5) + 9 = (1+ 8) * 4 + 9 = 45;
• 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100 = (1 + 100) * 50 = 5050

Задача 2

Имеется 9 гирь весом 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г. Можно ли разложить эти гири на три кучки с равным весом?

С помощью правила Гаусса находим сумму всех весов:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) * 4 + 9 = 45 (г)

Далее смотрим, можно ли этот вес разбить на три равных веса:

Значит, если мы сможем сгруппировать гири так, чтобы в каждой кучке были гири суммарным весом 15г, то задача решена.

Один из вариантов:

Другие возможные варианты найдите сами с ребенком.

Обратите внимание ребенка на то, что когда решаются подобные задачи лучше всегда начинать группировать с большего веса (числа).

Задача 3

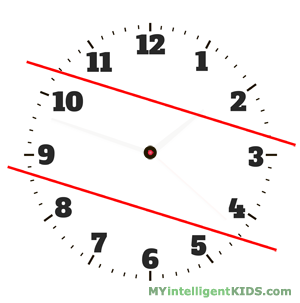
Можно ли разделить циферблат часов прямой линией на две части так, чтобы суммы чисел в каждой части были равны?

Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим, делится ли она на 2:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78

Значит разделить можно. Теперь посмотрим как.

По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:

1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.

Следовательно, надо провести линию на циферблате так, чтобы 3 пары попали в одну половину, а три в другую.

Ответ: линия пройдет между числами 3 и 4, а затем между числами 9 и 10.

Задача 4

Можно ли провести на циферблате часов две прямые линией так, чтобы в каждой части сумма чисел была одинаковой?

Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим делиться ли она на 3:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78

78 делиться на 3 без остатка, значит разделить можно. Теперь посмотрим как.

По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:

1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.

Следовательно, надо провести линии на циферблате так, чтобы в каждую часть попали по 2 пары.

Ответ: первая линия пройдет между числами 2 и 3, а затем между числами 10 и 11; вторая линия — между числами 4 и 5, а затем между 8 и 9.

Задача 5

Летит стая птиц. Впереди одна птица (вожак), за ней две, потом три, четыре и т. д. Сколько птиц в стае, если в последнем ряду их 20?

Получаем, что нам необходимо сложить числа от 1 до 20. А к вычислению такой суммы можно применить правило Гаусса:

1 + 2 + 3 + 4 + 5 + … + 15 + 16 + 17 + 18 + 19 + 20 = (20 + 1) * 10 = 210.

Задача 6

Как рассадить 45 кроликов в 9 клеток так, чтобы во всех клетках было разное количество кроликов?

Если ребенок решил и с пониманием разобрал примеры из задания 1, то тут же вспоминается, что 45 это сумма чисел от 1 до 9. Следовательно, сажаем кроликов так:

• первая клетка — 1,
• вторая — 2,
• третья — 3,
• …
• восьмая — 8,
• девятая — 9.

Но если ребенок сразу не может сообразить, то попробуйте натолкнуть его на мысль о том, что подобные задачи можно решить перебором и надо начинать с минимального числа.

Задача 7

Вычислить сумму, используя прием Гаусса:

• 31 + 32 + 33 + … + 40;
• 5 + 10 + 15 + 20 + … + 100;
• 91 + 81 + … + 21 + 11 + 1;
• 1 + 2 + 3 + 4 + … + 18 + 19 + 20;
• 1 + 2 + 3 + 4 + 5 + 6;
• 4 + 6 + 8 + 10 + 12 + 14;
• 4 + 6 + 8 + 10 + 12;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11.

• 31 + 32 + 33 + … + 40 = (31 + 40) * 5 = 355;
• 5 + 10 + 15 + 20 + … + 100 = (5 + 100) * 10 = 1050;
• 91 + 81 + … + 21 + 11 + 1 = (91 + 1) * 5 = 460;
• 1 + 2 + 3 + 4 + … + 18 + 19 + 20 = (1 + 20) * 10 =210;
• 1 + 2 + 3 + 4 + 5 + 6 = (1 + 6) * 3 = 21;
• 4 + 6 + 8 + 10 + 12 + 14 = (4 + 14) * 3 = 54;
• 4 + 6 + 8 + 10 + 12 = (4 + 10) * 2 + 12 = 40;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = (1 + 10) * 5 + 11 = 66.

Задача 8

Имеется набор из 12 гирек массой 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г, 10г, 11г, 12г. Из набора убрали 4 гирьки, общая масса которых равна трети общей массы всего набора гирек. Можно ли оставшиеся гирьки расположить на двух чашках весов по 4 штуки на каждой чашке так, чтобы они оказались в равновесии?

Применяем правило Гаусса, чтобы найти общую массу гирек:

1 + 2 + 3 + … + 10 + 11 + 12 = (1 + 12) * 6 = 78 (г)

Вычисляем массу гирек, которые убрали:

Следовательно, оставшиеся гирьки (общей массой 78-26 = 52г) надо расположить по 26 г на каждую чашу весов, чтобы они оказались в равновесии.

Нам не известно какие гирьки были убраны, значит мы должны рассмотреть все возможные варианты.

Применяя правило Гаусса можно разбить гирьки на 6 пар с равным весом (по 13г):

1г и 12г, 2г и 11г, 3г и 10, 4г и 9г, 5г и 8г, 6г и 7г.

Тогда лучший вариант, когда при убирании 4 гирек уберутся две пары из приведенных выше. В этом случае у нас останутся 4 пары: 2 пары на одну чашу весов и 2 пары на другую.

Худший вариант — это когда 4 убранные гирьки разобьют 4 пары. У нас останутся 2 неразбитые пары общим весом 26г, значит их помещаем на одну чашу весов, а оставшиеся гирьки можно поместить на другую чашу весов и они тоже будут 26г.

Источник

Математика

Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет

С этой картой можно накопить на мечту, жми ⇒

План урока:

Мудрая Сова: Здравствуйте, дорогие ребята! Вы меня узнали? Конечно, это я, мудрая Сова!

Я рада приветствовать вас снова в нашей лесной школе. Мои верные друзья : черепашка Маша, кошка Алиса и енот Кузьма отлично отдохнули летом и готовы помогать вам изучать математику в третьем классе.

Вы все помните, что мы с вами изучали в прошлом году? Давайте проверим ваши знания.

В прошлом году наши уроки начинались с устного счета. Напомните, для чего он нужен? Правильно, для того, что разогреть наш мозг и подготовиться решать примеры и задачи.

Кузьма уже подготовил вам задания для устного счета.

1. Задание для устного счета

36 увеличьте на 8.

На сколько 18 больше 9?

Уменьшите 17 на 8.

19 меньше неизвестного числа на 12. Чему равно неизвестное число?

Найдите сумму чисел: 16 и 17.

Вычислите значение разности чисел: 24 и 16.

Сумма каких однозначных чисел равна 16?

Для детского сада купили 16 кукол, а мячей на 9 меньше. Сколько мячей купили для детского сада?

Сыну 22 года. Его отцу 50 лет. На сколько лет сын моложе отца?

Ответы в конце урока!

Повторяем состав чисел

Сова: Хорошо. Посмотрим, как ребята помнят состав чисел. Что такое состав чисел? Правильно. Это два числа, из которых состоит каждое число. А зачем нам нужно знать состав чисел? Чтобы быстро считать удобным способом.

Давайте вспомним, как мы это делали во втором классе. Например, нам нужно найти сумму чисел 23 и 50. Что мы с вами будем делать? Разложим число 27 на два слагаемых: 20 и 7. Теперь нам легче будет сложить десятки и к полученной сумме прибавить три единицы.

Вспомнили? Решите несколько примеров, используя свои знания о составе чисел.

Сова: Молодцы, ребята! О, черепашке Маше уже не терпится решать с вами задачи. Что ты ребятам сегодня приготовила?

Решаем задачи различными способами

Черепашка Маша: Мы сегодня с ребятами вспомним, как решать задачи разными способами.

Задание 2. Найдите из предложенных утверждений правильные:

Задачу можно решить по действиям с пояснениями или по вопросам.

Задачу можно решить, используя свой опыт. V

Задачу можно решить выражением.

Задачу можно решить арифметически. V

Задачу можно решить алгебраически . V

Задачу можно решить графически. V

Ответ в конце урока!

Вспомним, что значит решить задачу, используя свой опыт? Помните, в первом классе мы еще не знали сложение и вычитание, но используя палочки или другой счетный материал, мы решали задачи про птиц, которые прилетели или улетели, про морковки и зайцев, пересчитывая их. Это и есть наш опыт.

Познакомившись с понятием сложение и вычитание, мы стали записывать решение уже арифметически, с помощью примеров.

Задачи на умножение и деление мы решали с помощью чертежа или рисовали схему – это графический способ.

А уравнения мы решаем, каким способом? Правильно, алгебраическим, т.к. неизвестное число обозначали латинской буквой и находили его значение.

Вот вам три задачи, которые нужно решить, выбрав один из известных вам способов и указать его в ответе.

Задача 1. Почтальон разнес 47 писем. Ему осталось разнести еще 15. Сколько всего писем оно должен разнести?

47 + 15 = 62 (письма) – арифметический способ.

Задача 2. Красная шапочка сначала шла до автобусной остановки 10 минут, потом ехала на автобусе 39 минут, и затем, до бабушкиного дома её подвез Буратино. Всего в пути Красная шапочка была час. Сколько минут её катал на велосипеде Буратино?

Решили графическим способом.

Задача 3. В школьную библиотеку из второго класса записалось 46 школьников. Девочек, 24 , остальные мальчики. Сколько мальчиков записалось в школьную библиотеку?

Решили алгебраическим способом.

Сова: Ай да ребята! Ай да молодцы! Как ловко вы решаете задачи различными способами. Пришло время немного отдохнуть.

Определяем верные и неверные равенства

Сова : Продолжаем работать. Вспомним, что такое равенство и неравенство?

Равенство это когда левая часть выражения (примера) равна правой. Например, 12+4 = 16. В равенстве используют знак «=»

А неравенство – левая часть выражения больше или меньше правой. Например, 12+4

Повторили? А теперь, закрепим.

Задача 4. Вам нужно будет выписать только неверные неравенства.

(Правильные ответы выделены курсивом)

А кто у нас тут, рисует различные геометрические фигуры? Алиса!

Геометрические фигуры и задачи

Кошка Алиса: Мур, мур! Да, я люблю рисовать различные геометрические фигуры. А ребята помнят геометрические фигуры?

Задача 5. Назовите все геометрические фигуры, которые видите.

Сова: Ну что скажешь, Алиса, знают ребята геометрические фигуры?

Алиса: Мур, мур, знают. А вот, помнят они, как чертить отрезки, делить их и обозначать буквами?

Сова: А ты проверь. Дай им задачу и посмотри, помнят или забыли за лето?

Алиса: Хорошо. Вот вам геометрическая задача.

Задача 6. Начертите в тетради отрезок АВ длиной 1 дм 2 см. Разделите его точками на три равные части. Обозначьте буквами отмеченные точки. Запишите все полученные отрезки.

Ответ в конце урока!

Алиса: Великолепно! Мур, мур. Молодцы, ребята! Пойду придумывать вам новые геометрические задачи.

Логическая задача от мудрой Совы

Сова: Наш урок подходит к концу. Но у меня для вас есть задача на смекалку.

Задача 7. В записи 8 8 8 8 8 8 поставьте между некоторыми цифрами два знака действия и скобки так, чтобы полученное выражение имело значение

Правильный ответ в конце урока!

Ребята, давайте подведем итоги нашего сегодняшнего урока.

Сегодня мы повторили темы:

-решение задач различными способами;

-верные и неверные равенства;

И давайте сверим ответы:

Задание 1. 44, 9,9,31,33,8,8,7,28

Задание 2. (правильные ответы выделены V )

Первое и третье утверждение о формах записи задачи, а не способ их решения.

Задача 6. АС, СD, DB.

Задача 7.

1. (88-88) х 88 = 0 х 88 = 0

2. (888-88):8 = 800 : 8 = 100

Спасибо моим друзьям: Кузьме, Маше и Алисе за помощь в проведении урока.

Источник