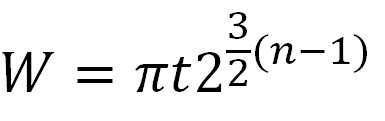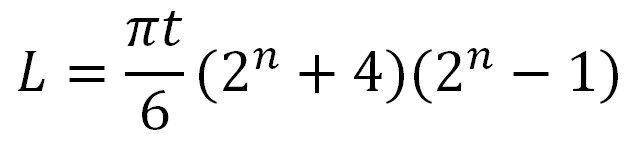- Сложить лист бумаги 7 раз? Нет проблем, если у вас есть гидравлический пресс
- masterok
- Мастерок.жж.рф
- Хочу все знать
- Почему бумагу нельзя свернуть больше 7 раз? А если она стоит 85$ за рулон?
- Правдива ли история про английских лучников, средний палец и происхождение выражения f#ck you?
- Молдавские учёные решили проблему, над которой 140 лет бились математики всего мира
- Они улетели и не вернутся никогда. Вояджеры
- Иррациональные число «Пи»
- Отбор эмбрионов, направленный на обеспечение интеллекта детей. Реальная услуга с сомнительными результатами
- Все страны на планете занимают меньше трети поверхности нашей планеты
- Трехмерная реконструкция синапса
- Умный мозг не только большой, но и жаждущий крови
- Научный метод в музыке — Роман Олейников
- Реставрирую шкаф
- Что, если наш 4D мир станет пятимерным?
Сложить лист бумаги 7 раз? Нет проблем, если у вас есть гидравлический пресс

Возможно это, силен если ты!
Пробовали ли вы когда-нибудь складывать обычный лист бумаги? Вероятно, да. Один, два, три раза — не проблема. Потом уже тяжелее. Стандартный лист бумаги формата А4 вряд ли кто сможет сложить боле 7 раз без подручных средств. Все это объясняется наличием физического феномена — многократно складывать лист бумаги не получается из-за быстроты роста показательной функции.
Как говорит Википедия, количество слоёв бумаги равняется двум в степени n, где n — количество складываний бумаги. Например: если бумагу сложили пополам пять раз, то количество слоёв будет два в степени пять, то есть тридцать два. И для обычной бумаги можно вывести уравнение.
Уравнение для обычной бумаги:

где W — ширина квадратного листа, t — толщина листа и n — количество выполненных сгибаний вдвое.
В использовании длинной полосы бумаги требуется точное значение длины L:

где L — минимально возможная длина материала, t — толщина листа и n — количество выполненных сгибаний вдвое. L и t должны быть выражены в одних и тех же единицах.
Если взять не обычную бумагу плотностью 90 г/дм3 (или чуть больше/меньше), а кальку или даже золотую фольгу, то сложить такой материал можно чуть более количество раз — от 8 до 12.
«Разрушители легенд» (Mythbusters) как-то решили проверить закон, взяв лист бумаги размером с футбольное поле (51,8×67,1 м). Используя такой нестандартный лист, им удалось сложить 8 раз без специальных средств (11 раз с применением катка и погрузчика). По утверждению поклонников телепередачи, калька от упаковки офсетной печатной формы формата 520×380 мм при достаточно небрежном складывании без усилий складывается восемь раз, с усилиями — девять. При этом каждый из сгибов должен быть перпендикулярен предыдущему. Если сгибать под другим углом, можно добиться того, что количество сгибаний будет чуть большим (но не всегда).
Вот еще немного попыток:
Ну, а что, если складывать лист бумаги не руками, а взять себе в помощники гидравлический пресс? Давайте посмотрим, что тогда выйдет. Учтите только, что ролик — на английском, с очень сильным акцентом (арабским финским).
Источник
 masterok
masterok
Мастерок.жж.рф
Хочу все знать
Уже давно ходит такая распространённая теория, что ни один лист бумаги нельзя сложить вдвое больше семи (по некоторым данным — восьми) раз. Источник этого утверждения уже сложно найти. Между тем текущий рекорд складывания – 12 раз. И что удивительнее, принадлежит он девушке, математически обосновавшей эту «загадку бумажного листа».
Разумеется, мы говорим о бумаге реальной, имеющей конечную, а не нулевую, толщину. Если складывать её аккуратно и до конца, исключая разрывы (это очень важно), то «отказ» складываться вдвое обнаруживается, обычно, уже после шестого раза. Реже – седьмого.
Попробуйте проделать это сами с листком из тетради.
И, как ни странно, от размеров листа и его толщины ограничение мало зависит. То есть, просто так взять тонкий лист побольше, да и сложить его вдвое, раз допустим 30 или хотя бы 15 – не получается, как ни бейся.
В популярных подборках, типа «А знаете ли вы что…» или «Удивительное рядом», факт сей — что вот больше именно 8 раз сложить бумагу нельзя — до сих пор можно найти очень во многих местах, в Сети и вне. Но факт ли это?
Давайте рассуждать. Каждое сложение удваивает толщину кипы. Если толщину бумаги принять равной 0,1 миллиметра (размер листа мы сейчас не рассматриваем), то сложение её вдвое «всего» 51 раз даст толщину сложенной пачки в 226 миллионов километров. Что уже очевидный абсурд.
Мировая рекордсменка Бритни Гэлливан и бумажная лента, сложенная вдвое (в одном направлении) 11 раз
Кажется, тут-то мы начинаем понимать, откуда берётся известное многим ограничение на 7 или 8 раз (ещё раз – бумага у нас реальная, она не тянется до бесконечности и не рвётся, а порвётся – это уже не складывание). И всё же…
В 2001 году одна американская школьница решила вплотную заняться проблемой двойного складывания, а получилось из этого целое научное исследование, да ещё и мировой рекорд.
Собственно, началось всё с вызова, брошенного педагогом ученикам: «А вот попробуйте сложить хоть что-нибудь пополам 12 раз!». Мол, убедитесь, что это из разряда совершенно невозможного.
Бритни Гэлливан (Britney Gallivan) (заметим, сейчас она уже студентка) поначалу отреагировала как Алиса Льюиса Кэрролла: «Бесполезно и пробовать». Но ведь говорила Алисе Королева: «Осмелюсь сказать, что у вас не было большой практики».
Вот Гэлливан и занялась практикой. Порядком намучившись с разными предметами, она сложила-таки лист золотой фольги вдвое 12 раз, чем посрамила своего преподавателя.
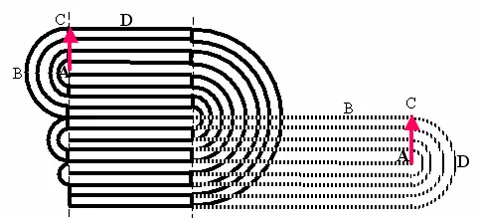
Пример складывания листа вдвое четыре раза. Пунктир – предыдущее положение трёхкратного сложения. Буквы показывают, что точки на поверхности листа смещаются (то есть, листы скользят друг относительно друга), и занимают в результате не то положение, как может показаться при беглом взгляде
На этом девушка не успокоилась. В декабре 2001 года она создала математическую теорию (ну, или математическое обоснование) процесса двойного складывания, а в январе 2002 года проделала 12-кратное складывание пополам с бумагой, используя ряд правил и несколько направлений складывания (для любителей математики, несколько подробнее — тут).
Бритни заметила, что к этой проблеме ранее уже обращались математики, но правильного и проверенного практикой решения задачи ещё никто не предоставлял.
Гэлливан стала первым человеком, который правильно понял и обосновал причину ограничений на сложение. Она изучила накапливающиеся при складывании реального листа эффекты и «потерю» бумаги (да и любого иного материала) на сам сгиб. Она получила уравнения для предела складывания, для любых исходных параметров листа. Вот они.
Первое уравнение относится к складыванию полосы только в одном направлении. L — минимально возможная длина материала, t – толщина листа, и n — число выполненных сгибов в два раза. Разумеется, L и t должны быть выражены в одних и тех же единицах.
Во втором уравнении речь идёт о складывании в различных, переменных, направлениях (но всё равно – вдвое каждый раз). Здесь W – ширина квадратного листа. Точное уравнение для складывания в «альтернативных» направлениях – более сложное, но здесь приводится форма, дающая очень близкий к реальности результат.
Для бумаги, которая не является квадратом, вышеупомянутое уравнение всё ещё даёт весьма точный предел. Если бумага, скажем, имеет пропорции 2 к 1 (по длине и ширине), легко сообразить, что нужно сложить её один раз и «привести» к квадрату двойной толщины, а затем воспользоваться вышеупомянутой формулой, мысленно держа в уме одно лишнее складывание.
В своей работе школьница определила строгие правила двойного сложения. Например, у листа, который свёрнут n раз, 2n уникальных слоёв обязаны лежать подряд на одной линии. Секции листа, не удовлетворяющие этому критерию, не могут считаться как часть свёрнутой пачки.
Так вот Бритни и стала первым в мире человеком, сложившим лист бумаги вдвое 9, 10, 11 и 12 раз. Можно сказать, не без помощи математики.
А в 2007 году команда «Разрушителей легенд» решила сложить огромный лист, размером с половину футбольного поля. В итоге они смогли сложить такой лист 8 раз без специальных средств и 11 раз с применением катка и погрузчика.
Источник
Почему бумагу нельзя свернуть больше 7 раз? А если она стоит 85$ за рулон?
Сегодня мы вспомним всем известное поверье, которое гласит, что лист бумаги нельзя свернуть больше 7 раз. Многие из Вас, особенно в детстве, я уверен, пробовали провернуть этот трюк и всё время сталкивались с непреодолимыми трудностями. Сегодня пришло время решить этот вопрос раз и навсегда! Поехали!
Рекорд по сворачиванию листа бумаги
Сразу хотелось бы сказать, что максимальное количество сворачиваний бумаги — 12, а рекорд принадлежит девушке — Бритни Гэлливан.
Однако условия, в которых проводились «складывания» слишком далеки от тех, которые Вы можете воспроизвести в комнате. Например, для своего рекорда Бритни использовала 1200 (. ) метров специальной туалетной бумаги стоимость 85$ за рулон. Только тогда бумагу удалось сложить пополам 12 раз.
Естественно речь идет о реальном складывании бумаги, которая обладает ненулевой толщиной. Также важно отметить, что не должны допускаться разрывы.
Перед бумагой, девушка успешно сложила 12 раз золотую фольгу, намного меньшей толщины. Основной критерий успешности складывания — точки перегиба должны лежать на одной линии.
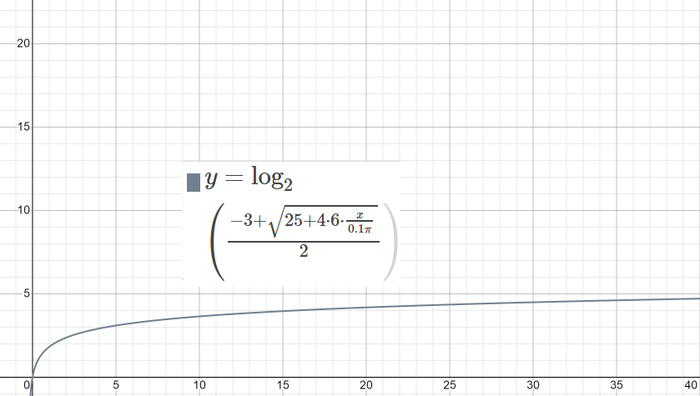
Бритни, на 2001 год, бывшая еще школьницей,не только представила практическое решение этой проблемы, но и вывела формулы, достаточно точно отражающие потери бумаги при складывании:
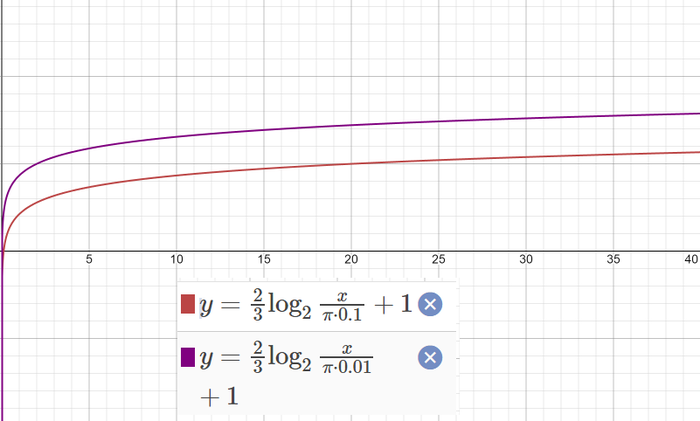
В этой формуле W — это ширина бумаги, t — толщина, n — количество складываний. Толщина и ширина, естественно, должны быть выражены в одних величинах. Если выразить n из этой формулы и построить график зависимости от ширины бумаги, получим следующее :
0.1 мм — стандартная толщина листа А4. Если подставить вместо х реальный размер листа а4, получится 6-7 складываний.
Вторая функция — для продолговатых листов бумаги
L — длина листа бумаги, t — толщина. Решив уравнение как квадратное относительно 2^n,можно построить такой график:
Если подставить в эту формулу длину туалетной бумаги, равную 1200 метров, то получим как раз те «рекордные» 12 складываний.
В программе «Разрушители легенд» в 2007 году предпринимались попытки разрушить или подтвердить этот миф. Для этого участники шоу сворачивали лист бумаги размером с половину футбольного поля (примерно 50 на 70 м). Без применения укладчика это удалось сделать всего лишь 8 раз, а с применением — 11.
Подводя итоги, скажу, что основной причиной невозможности сложить лист бумаги сколько угодно раз является скорость роста слоев бумаги. В то время, как она растет экспоненциально, возможности по увеличению размеров листа бумаги и затрат на это растут в лучшем случае линейно. Если только представить, что стандартную бумагу можно сложить 51 раз, ёё толщина должна составить несколько сот миллионов километров!
«Если только представить, что стандартную бумагу можно сложить 51 раз, ёё толщина должна составить несколько сот миллионов километров’ И тут же «Больше математики в Телеграм — Математика не для всех.»
Но математика это можно сказать основа или даже мамаша всех точных наук! А тут несколько сот миллионов километров. И какова кстати толщина «стандартной» бумаги?
Ну а с количеством слоёв справится и калькулятор. Их кстати
Такие прекрасные формулы и такая отвратительная постановка задачи.
Если под «сворачиванием» представить форму сгибания в виде буквы Z, то пока длины хватит
Нет, она растет в геометрической прогрессии.
Если в гармошку, сначала в одну сторону, потом в другую, у меня получилось 196 слоёв, обща толщина в 30 мм, длина отхлёста, почти 5 сантиметр (если дальше складывать 5 см отхлёст, бумага трескается)
Правдива ли история про английских лучников, средний палец и происхождение выражения f#ck you?
В соцсетях можно встретить забавную историю о том, что происхождение известного жеста и не менее распространённого ругательства берёт начало от битвы при Азенкуре, состоявшейся в 1415 году. Мы проверили, так ли это на самом деле.
(Спойлер для ЛЛ: неправда)
Контекст. Пользователи соцсетей рассказывают такую историю: в 1415 году в ходе Столетней войны состоялась битва при Азенкуре между французами и англичанами. Французы якобы договорились, что будут отрезать захваченным в плен лучникам средний палец — без него противники не смогут стрелять из длинного лука, представлявшего серьёзную опасность. Эти луки делались из тиса, а стрельбу из них якобы называли щипанием (по-английски pluck yew). После победы англичане якобы стали насмехаться над противниками, показывая средний палец и как бы говоря тем самым, что продолжат «щипать тис». Утверждается, что со временем фраза pluck yew трансформировалась в распространённое в современном английском языке ругательство fuck you. Эту байку можно обнаружить в популярных пабликах во «ВКонтакте» и Facebook, в Twitter, LiveJournal, на сайтах издания «Новые известия» и некоторых школ английского языка. Не миновала она и Пикабу FUCK YOU! Как возник жест , где была, отметим, довольно оперативно разоблачена.
Современные учёные придерживаются мнения, что демонстрация среднего пальца приобрела своё символическое значение задолго до Столетней войны. По словам антрополога Десмонда Морриса, «это один из самых древних из известных нам жестов». Специалист уверен, что он происходит из первобытных времён, а его символика довольно проста: средний палец — пенис, сжатые пальцы — тестикулы.
Использование подобного жеста можно встретить уже в античные времена. Так, в сочинениях Диогена Лаэртского упоминается история, связанная с Диогеном Синопским — якобы тот указал на Демосфена именно средним пальцем со словами:
«Вот вам правитель афинского народа». Там же описан другой эпизод: «Большинство людей, говорил он (Диоген Синопский. — Прим. ред.), отстоит от сумасшествия на один только палец: если человек будет вытягивать средний палец, его сочтут сумасшедшим, а если указательный, то не сочтут».
Жест сохранился и в Древнем Риме. Например, в эпиграмме Марциала говорится:
«Смейся, Секстилий, над теми, кто называет тебя педерастом, и показывай им средний палец».
В другой его эпиграмме рассказывается о старике, который хвастается отменным здоровьем и демонстрирует врачам «неприличный» палец. Использование этого жеста в Древнем Риме описывает и американский исследователь Энтони Корбелл.
Но вернемся к Столетней войне. Современные историки, занимающиеся этим историческим периодом, не согласны с популярной в интернете байкой. Энн Карри, профессор Университета Саутгемптона и бывший вице-президент Королевского исторического общества, посвятила целую книгу битве при Азенкуре. В ней исследовательница пишет:
«Ни в одной хронике или историческом сочинении XVI века нет сообщений о том, что английские лучники показывали какие-либо жесты французам после битвы, чтобы продемонстрировать тем, что у них всё ещё есть пальцы. Нет никаких доказательств тому, что при захвате лучника тем или иным способом противник отрезал ему пальцы».
Схожую оценку даёт и американский историк Джон Киган.
Возможный первоисточник популярной легенды — хроника XV века, написанная французом Жаном де Вавреном. В ней говорится, что в своей речи перед битвой английский король Генрих V якобы заявил:
«Французы хвастались, что они отрежут по три пальца с правой руки всех попавших в плен лучников, чтобы впоследствии ни один воин или конь не был убит с помощью их луков».
Подлинность этого утверждения весьма сомнительна — присутствие французского хрониста при выступлении английского короля в условиях войны представляется маловероятным.
Что касается связи между неприличным выражением fuck you и староанглийским словосочетанием pluck yew («щипание тиса»), то и это утверждение не находит подтверждения среди учёных. Хотя происхождение глагола fuck до сих пор не удалось установить однозначно, версия с причастностью английских лучников не входит в число сколько-нибудь вероятных. Наиболее популярные варианты, предлагаемые лингвистами, — развитие одного из древнеанглийских корней или заимствование из других германских языков. Возможное самое раннее упоминание глагола относится к началу XIV века — битва при Азенкуре состоялась спустя 100 лет.
Таким образом, все тезисы популярной в интернете истории не соответствуют действительности. Английские лучники точно не «изобрели» неприличный жест в 1415 году. О планах французов отрезать им средний палец доподлинно не известно — о подобной угрозе якобы рассказывал перед битвой английский король, причём зафиксировано это в единственной французской хронике. Наконец, самое раннее упоминание глагола fuck обнаружено в документе, составленном за более чем сто лет до битвы при Азенкуре, поэтому его связь со словом pluck крайне сомнительна.
Ещё нас можно читать в Телеграме, в Фейсбуке и в Вконтакте. Традиционно уточняю, что в сообществах отсутствуют спам, реклама и пропаганда чего-либо (за исключением здравого смысла), а в день обычно публикуем не больше двух постов.
Аудиоверсии проверок в виде подкастов c «Коммерсантъ FM» доступны в Simplecast, «Яндекс.Подкасты», Apple Podcasts, «ЛитРес», Soundstream.
Почитать по теме:
Молдавские учёные решили проблему, над которой 140 лет бились математики всего мира
Два математика из Молдовы первыми в мире решили алгебраическую проблему, над которой 140 лет размышляли великие ученые мира. Об этом на этой неделе сообщил Технический университет Молдовы (UTM).
«Доктор физико-математических наук Михаил Попа и доктор математических наук Виктор Прикоп первыми в мире нашли решение знаменитой проблемы центра и фокуса, поставленной выдающимся французским математиком Анри Пуанкаре, над которой великие математики мира размышляли более века», — говорится на сайте университета.
Этой проблеме посвятили тысячи работ математики из Франции, России, Беларуссии, Китая, Великобритании, Канады, США и других стран мира. Только в Молдове число работ, посвященных проблеме Пуанкаре, приближается к сотне, отметили в UTM.
Профессор университета Михаил Попа, основатель научной школы алгебры Ли и дифференциальных систем, предложил собственное решение проблемы центра и фокуса, которое привело его к результату, ставшему открытием.
Во время исследований к профессору присоединился его ученик Виктор Прикоп. Вместе они усовершенствовали первоначальную гипотезу в монографии «Проблема центра и фокуса. Алгебраические решения и гипотезы».
Работа была переведена на английский язык и представлена для издания в несколько зарубежных издательств. В итоге лучшие условия предложил издательский дом «Taylor & Francis Group», расположенный в Великобритании и специализирующийся на публикациях научной литературы и журналов.
Где-то всплакнул Гриша Перельман.
Панорама, да не та. И с такими лицами не шутят.
Они улетели и не вернутся никогда. Вояджеры
Проект «Вояджер» – один из самых масштабных и успешных космических проектов, созданных человечеством. Ученые до сих пор изучают данные, собранные в рамках миссии, а аппарат «Вояджер-1» является самым отдаленным объектом, который создал человек.
Но обо всем по порядку:
В середине 60-х годов в своей работе о гравитационных маневрах и полетах к дальним планетам один никому не известный студент-интерн указал на удачное сближение сразу четырех планет: Юпитера, Сатурна, Урана и Нептуна. Таким событием, конечно же, заинтересовались ученые из NASA, и уже в 1969 году был готов проект по запуску 4 автономных космических аппаратов, которые смогли бы максимально близко подлететь к планетам и изучить все их разом. Но финансирование урезали – денег хватило только на 2. Аппараты отправили в космос 20 августа и 5 сентября 1977 года, назвав проект «Вояджер» (с англ. «Путешественник») буквально за несколько дней до старта.
Чего только не было на борту Вояджеров: и камеры в высоком разрешении с разным углом обзора, и спектрометры с многочисленными настройками, детекторы плазмы, космических лучей, волн всяческих… В общем, вооружили их до зубов и на все случаи жизни.
«А как это все будет работать? Они же не от пальчиковых батареек энергию берут?» Как раз от батареек, только не от пальчиковых, а от космических батареек РИТЭГ (радиоизотопный термоэлектрический генератор). В них используется радиоактивный плутоний, который выделяет тепло при своем распаде, а генератор превращает ее в электричество. Это не ядерный реактор на атомной станции, конечно, и энергии от него гораздо меньше, зато размеры РИТЭГа весьма скромные и он не требует обслуживания на протяжении всего срока работы.
К борту каждого из аппаратов был прикреплен диск с посланием внеземным цивилизациям. На пластинке записаны приветствия на разных языках, звуки Земли, классическая музыка, изображения земных пейзажей и многое другое. До сих пор не утихают споры о целесообразности и безопасности таких посланий. Делались они с твердой верой во внеземной разум или чтобы «увековечить» себя во Вселенной – не ясно. На эту тему у меня есть отдельный пост «Золотое послание Вояджера».
В чем же значимость проекта?
Программа «Вояджер» создавалась для исследования Юпитера и Сатурна, о которых в то время было известно очень мало, а так же для исследования спутников этих планет. Но миссия не ограничилась только этим. Сбор данных начался уже через несколько дней после старта. Выйдя в открытый космос и встав на свой курс, «Вояджер-1» передал на Землю первую свою фотографию: Земля и Луна с расстояния 11 млн км.
К концу года оба аппарата вошли в Пояс астероидов и там, в бескрайней космической пустыне, «Вояджер-1» обогнал своего собрата, навсегда взяв лидерство в этой гонке. Ученые знали, что это произойдет, из-за этого «Вояджер-2» нарекли вторым номером, несмотря на то, что запустили его первым. В январе 1979 года «Вояджер-1» стал сближаться с Юпитером. Каждый день в одно и то же время аппарат делал несколько фотографий планеты, а ученые сложили из них занимательный «кинофильм». На нем видно как дуют ветра в атмосфере, как рождаются смерчи-воронки и как крутится Большое красное пятно. На фото Юпитер с расстояния 33 млн км.
Пролетая мимо Юпитера, «Вояджер-1» сделал примерно 19 тысяч снимков гигантской планеты и ее спутников, большинство из которых были удачными и четкими. Американский физик Эдвард Стоун сказал: «У нас набралось открытий почти на десятилетие вперед, за этот короткий двухнедельный период». Уже улетая от Юпитера, аппарат сделал финальные фото одного из спутников (Ио). Фильтр постобработки удалил белое пятно около поверхности, распознав в нем бесполезный шум, а вот ученые увидели совершенно иное – облако вулканического пепла. Это открытие просто взорвало научный мир! Впервые ученые увидели извержение вулкана вне Земли.
Следующим на очереди был Сатурн. Исследования этой планеты показали, что Сатурн холодный и совсем не спокойный уголок Солнечной системы. Температура атмосферы опускалась ниже -190°С, а скорость ветра достигала 1800 км/ч. Кроме всех прочих красот Сатурна, настоящий фурор вызвал снимок одного из его спутников – Мимаса. Он удивительно схож со Звездой смерти из фильма «Звездные войны», который на тот момент только вышел на экраны.
«Вояджер-2» тоже не отставал. Вслед за своим «напарником» он продолжил изучать атмосферу Сатурна, систему его колец, а так же пролетел на бреющем полете мимо Энцелада – спутника Сатурна. На этом месте пути двух «братьев» разошлись. В 1981 году «Вояджер-2» круто поменял траекторию, направившись к Урану и Нептуну. Уже в 1986 году аппарат передал на Землю тысячи снимков Урана. Кстати, для этого на Земле пришлось модернизировать принимающие антенны, ведь расстояние до аппарата стремительно увеличивалось.
Прощание с Ураном
До 1986 года ученые знали про Уран лишь то, что он вращается на боку, у него есть 9 колец и 5 спутников. Уже первые снимки аппарата позволили открыть еще 2 кольца, а количество известных спутников увеличилось в 3 раза. При этом кольца были значительно моложе самой планеты. Вероятнее всего, Уран разрушил часть своих спутников приливными силами.
На очереди был Нептун и пока «Вояджер-2» летел к этой далекой планете, на нашей Земле вовсю проходила подготовка для приема слабеющего с каждым днем сигнала. Ранее модернизированные антенны приходилось дорабатывать вновь, причем существенно. Для лучшего приема антенны в разных частях света (Калифорния, Испания, Автралия) связали в одну единую сеть, а их диаметр расширили.
Нептун был последней планетой, с которой должен был встретиться Вояджер-2. Было решено пройти невероятно близко рядом с планетой — всего в 5 тыс. км от его поверхности (это было менее трех минут полета при скорости аппарата). Ювелирная работа, что сказать. Все маневры были заложены в аппарат заранее, ведь сигнал от Нептуна до Земли идет больше 4 часов! За это время «Вояджер-2» преодолеет свыше 200 тысяч километров и любая команда, направленная учеными, станет бесполезной. В декабре 1989 года камеры «Вояджера-2» были отключены навсегда. Позже были произведены несколько корректировок курса. На сегодняшний день часть приборов находится в рабочем состоянии. Ученые прогнозируют, что энергии батареи хватит до 2025 года.
В это же время «Вояджер-1», закончивший свою миссию, удалялся прочь от Солнца со скоростью 17 км/с. В феврале 1990 года Вояджер делает совместное фото всех планет Солнечной системы, среди которых есть и Земля. Фото, сделанное с расстояния 6 миллиардов километров, до сих пор остается самым удаленным снимком нашей планеты. Астрофизик и популяризатор науки Карл Саган много лет просил руководство проекта сделать это фото. С его легкой руки оно получило название «Бледно-голубая точка» (Pale Blue Dot). Снимок облетел весь мир и стал философским символом хрупкости нашего мира. Мира, который мы называем домом.
Сам Карл Саган сказал про этот снимок:
«Взгляните еще раз на эту точку. Это здесь. Это наш дом. Это мы. Все, кого вы любите, все, кого вы знаете, все, о ком вы когда-либо слышали, все когда-либо существовавшие люди прожили свои жизни на ней. Множество наших наслаждений и страданий, тысячи самоуверенных религий, идеологий и экономических доктрин, каждый охотник и собиратель, каждый герой и трус, каждый созидатель и разрушитель цивилизаций, каждый король и крестьянин, каждая влюбленная пара, каждая мать и каждый отец, каждый способный ребенок, изобретатель и путешественник, каждый преподаватель этики, каждый лживый политик, каждая «суперзвезда», каждый «величайший лидер», каждый святой и грешник в истории нашего вида жили здесь — на соринке, подвешенной в солнечном луче».
На сегодняшний день оба Вояджера удаляются прочь из Солнечной системы. Они уже пересекли гелиопаузу и вышли в межзвездное пространство. «Вояджер-1» остается самым удаленным рукотворным объектом. Расстояние до него 23 млрд километров (154 расстояния между Землей и Солнцем) и оно увеличивается каждую секунду! В 2027 году он должен удалиться от нас на один световой день. После 2030 года оба аппарата перейдут в режим радиомаяков из-за нехватки мощности, а к 2040 году умолкнут навсегда. Через 300 лет они приблизятся к внутренней границе облака Оорта, а после этого отправятся вечно странствовать по галактике Млечный путь.
Посмотреть за Вояджерами в реальном времени можно здесь.
Понравилась статья? Ставьте лайк и подписывайтесь, если еще не с нами.
Космос – это интересно!
Иррациональные число «Пи»
Вы знали, что математика, это не просто мир постоянных чисел, непонятных выражений и формул? Что это не однотонное полотно серых, или черных букв, которые сливаются в предложения и тексты?
Наука, это интересно! Как-то раз, я залез в пучины интернета, в поисках чего-нибудь интересного, я не знал куда движусь, и каждый шаг удивлял меня. В результате путешествия стало греческое иррациональное число «Пи» (π).
Сверху, одна из множества замечательных визуализаций иррационального числа, которое выглядит примерно так, и начинается со всем известного 3.14: «3,1415926535 8979323846 2643383279 5028841971. » — вид в десятичной системе исчисления, а если быть проще, нашими обыденными цифрами «0, 1, 2, 3, 4, 5, 6, 7, 8, 9». Правда, заметили те «. » (Три точки в конце)? Это и есть самое интересное — оно бесконечно!
Огромная работа, которую можно увидеть выше, была проделана Крживинским (учёный), который соединял струны друг с дружкой разноцветными нитями. К примеру тройку с единицей, затем с четвёркой, напомню что это начало числа «π» (Пи) — «3.14. «. И каждый раз, он менял цвет, как многие из называют «струн». Довольно красиво, не правда ли?)
В следующей визуализации процесс был очень похож на предыдущий, просто цифры, или точки, были изображены на краях изображения у виде кругов. Чем больше точка, тем более большой диаметр у круга.
Фиолетовые большие круги представляют собой девятки, которые в одном десятичном ряду повторяются шесть (6) раз. Это как раз те точки именуемые «точками Фейнмана», которые говорят, что: повторение происходит намного раньше, чем предсказывает вероятность.
Про число π (Пи) можно много чего рассказать даже не забираясь в графику. Довольно известный факт, что по нему можно легко узнать длину окружности, которая обозначается большой буквой C, по формуле C = 2πR, где R — радиус окружности. Или формулирование такого обозначения тоже возможно: Константа, которая отражает отношение длины окружности к ее диаметру.
Так-же это число, можно сказать «вхоже» в любую формулу, ведь хоть при описании окружности, хоть при повторении биения сердца, или орбиты Земли вокруг солнца, оно работает! Это удивительно!
Существует даже Международный День числа Пи (π) — 14 Марта. А в американском культуре, эта дата даже записывается в формате «3.14».
Последовательность цифр числа Пи (π) кажется случайной, но это и обозначает, что любая цифра начиная от 0, до 9, имеет равные шансы появится в одном десятичном ряду.. но действительно ли это так?
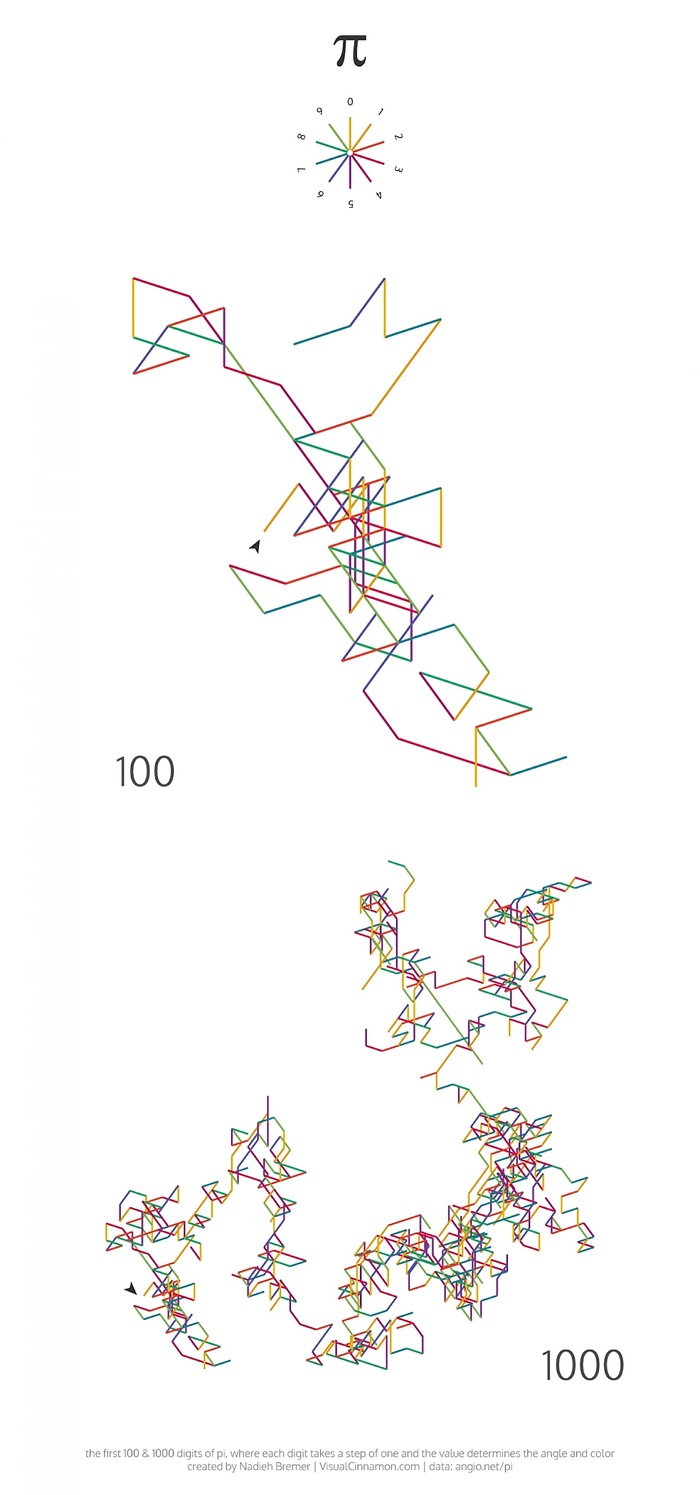
На иллюстрации выше, Вы можете видеть ещё одну из визуализаций этого загадочного числа. И вроде как исходя из работ астронома и аналитика Надие Бремера, где он изобразил, как число Пи (π) преодолевает барьеры 100, 1000, 10 000 и 100 000 тысяч цифр, можна сделать вывод, что оно случайно.
Но вот уже с 1706 года, когда Уильям Джонс ввёл число Пи (π), математики всего мира не могут прийти к одинаковому решению, ведь представьте, Вы стоите перед огромной мозаикой, вернее необратимо большой мозаикой — бесконечной. Но не на расстоянии хотя-бы 10-15 метров, а прямо лицом к лицу. Вы видите закономерность? Нет! С вашей точки зрения, в прямом и переносном смыслах её нет.
Но что скажет человек, глядя на эту же мозаику но уже с другого расстояния? Допустим метров 100. То же самое, ведь число бесконечно. Куда двигаться как увидеть то, что заполняет собой всё, и субъект, находящийся даже в любой точке этого пространства, всё время в объекте, и ничего не видит?
«Противоречие между порядком и случайностью – самый изысканный аспект Пи», — высказал интересную точку зрения Строгац.
Если сходу показать эти картинки, для многих людей они будут, и останутся просто картинками, но на самом деле, это визуализация того, как цифры могут «поместится» в графическом пространстве, и мощный инструмент для понимания математических закономерностей, правил.
Отбор эмбрионов, направленный на обеспечение интеллекта детей. Реальная услуга с сомнительными результатами
В специальном отчете, опубликованном в New England Journal of Medicine, возникают серьезные вопросы о преимуществах, рисках и этичности новой услуги, которую авторы называют «отбор эмбрионов на основе полигенных оценок» или ESPS. Услуга позволяет пациентам с экстракорпоральным оплодотворением отбирать эмбрионы с целью выбора более здоровых и даже более умных детей.
В отчете под названием «Проблемы с использованием полигенных оценок для отбора эмбрионов» многонациональная группа исследователей описывает ограничения услуги. Они также предупреждают, что пациенты и даже клиницисты по экстракорпоральному оплодотворению могут подумать, что эта услуга более эффективна и менее рискованна, чем она есть на самом деле.
Авторы подчеркивают, что, поскольку один и тот же ген часто влияет на множество разных признаков, выбор одного признака может привести к непреднамеренному отбору неблагоприятных признаков. Они также предупреждают, что использование сервиса может изменить демографические характеристики населения, усугубить социально-экономическое неравенство и обесценить определенные черты характера.
Если ESPS по-прежнему будет доступен для пациентов с ЭКО, исследователи призывают Федеральную торговую комиссию США разработать и обеспечить соблюдение стандартов ответственного обмена информацией об услуге. Авторы также призывают к общественному обсуждению этичного использования технологии и необходимости ее регулирования.
Несовершенный способ обеспечить здоровых детей
Полигенные оценки – это прогнозы индивидуального здоровья и других признаков, полученных в результате исследований генома. Было показано, что у взрослых полигенные оценки частично предсказывают эти исходы. Однако их предсказательная сила значительно снижается при сравнении эмбрионов друг с другом, поясняют авторы отчета.
«Полигенные оценки являются лишь слабыми предикторами большинства индивидуальных результатов у взрослых, особенно социальных и поведенческих черт, и есть несколько факторов, которые еще больше снижают их предсказательную силу в контексте отбора эмбрионов», – сказал соавтор отчета Патрик Терли. «Полигенные оценки предназначены для работы в иных условиях, чем клиника ЭКО. Эти слабые предикторы будут работать еще хуже при выборе эмбрионов».
Терли, который является директором Центра поведенческой и медицинской геномики в Центра экономических и социальных исследований Дорнсайф при Университете Южной Калифорнии, и его коллеги по исследованию изучали, является ли ESPS более эффективным для обеспечения здоровья в будущем, чем случайный отбор эмбрионов. Для этого они смоделировали ожидаемую разницу в риске будущего человека для нескольких заболеваний, сравнивая использование ESPS для выбора эмбриона с выбором одного жизнеспособного эмбриона случайным образом из 10. Они обнаружили, что в большинстве случаев снижение риска заболеваемости, который предлагает услуга, очень мал и весьма неопределенен.
В настоящее время несколько компаний работают с клиниками ЭКО, чтобы предложить услуги пациентам, которые хотят выбрать эмбрион с меньшими рисками развития диабета, рака, сердечных заболеваний, болезни Альцгеймера, воспалительного заболевания кишечника и шизофрении. Одна компания также предлагает услугу по отбору эмбрионов в соответствии с их прогнозируемым уровнем образования, семейным доходом и когнитивными способностями.
Недостатки службы подбора
Чтобы ESPS работал, полигенные оценки должны давать, по крайней мере, умеренно точные прогнозы относительно того, разовьются ли у выбранных эмбрионов определенный признак или нет. Исследования, в которых генерируются полигенные оценки, иногда предполагают умеренные или даже большие различия в фактических результатах между людьми с высокими и низкими оценками, но эти различия основаны на выборке людей из разных семей. Как отмечают Терли и его коллеги, ESPS обычно включает в себя сравнение членов одной семьи, что значительно снижает его прогностическую способность.
Кроме того, в исследованиях, которые производят полигенные оценки, участвуют люди со схожим происхождением и в основном европейские предки. В результате большинство построенных сегодня полигенных оценок будут менее предсказуемыми для людей других предков.
Наконец, оценки предсказательной силы полигенных показателей обычно предполагают очень похожие среды для поколения, включенного в исходное исследование, и поколения, которое родится в результате ESPS. Но к тому времени, когда эмбрион, выбранный службой, станет взрослым, человек может оказаться в совершенно ином окружении.
Широкое использование ESPS сопряжено и с другими рисками. Например, исследователи предупреждают, что использование услуги может усугубить существующие проблемы со здоровьем и другие диспропорции, поскольку она в основном доступна только относительно богатым и в настоящее время лучше всего работает среди тех, кто имеет европейское происхождение. Это также может усилить предрассудки и дискриминацию, сигнализируя о том, что существующие люди с чертами, против которых делают отбор родители, менее ценны.
«В некоторых странах есть органы власти, которые решают, на какие признаки эмбрионов можно тестировать», – сказала Мишель Н. Мейер, доцент кафедры биоэтики и юрист Geisinger Health System и соавтор специального доклада. «Но в США существует сильная юридическая и этическая традиция рассматривать репродуктивные решения как вопрос личного индивидуального выбора. В краткосрочной перспективе FTC должна помочь установить, что считается адекватным доказательством в поддержку заявлений об ожидаемых преимуществах ESPS и что считается адекватным раскрытием информации в данном контексте».
Исследователи также призывают профессиональные медицинские сообщества разработать политику и рекомендации, а сами компании – продемонстрировать, что информация, которую они предоставляют различным клиентам, является полной, точной и понятной.
Они также говорят, что в обществе необходимо обсудить, могут ли существующие правовые рамки адекватно обеспечивать точную информацию о ESPS, и следует ли принять ограничения на использование услуги.
«Многие индивидуальные репродуктивные решения, принимаемые на протяжении поколений, могут иметь глубокие социальные последствия», – сказал соавтор отчета Дэниел Дж. Бенджамин,. «В совокупности эти решения могут изменить демографические характеристики населения, усугубить неравенство и обесценить черты, против которых отбираются».
Больше околонаучного на канале t.me/everScience.
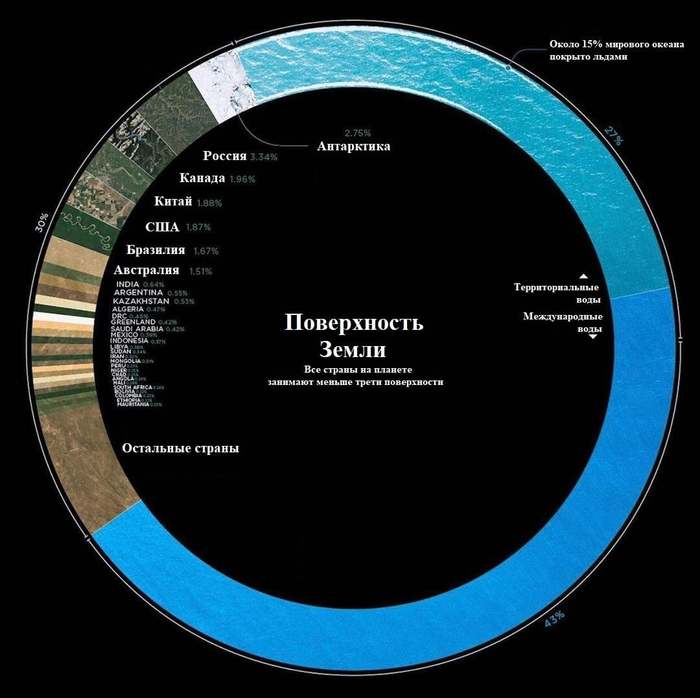
Все страны на планете занимают меньше трети поверхности нашей планеты
Поверхность Земли — это более 510 миллионов квадратных километров, но менее 30% из них, скажем так, является поверхностью в привычном нам понимании. Остальное — вода.
Крупнейшими странами по площади являются Россия (3,35%), Канада (1,96%) и Китай (1,88%). Вместе они занимают примерно 7,2% всей поверхности Земли.
С помощью этой инфографики вы сможете наглядно оценить эти и другие данные о поверхности нашей планеты. Больше околонаучного на канале t.me/everScience.
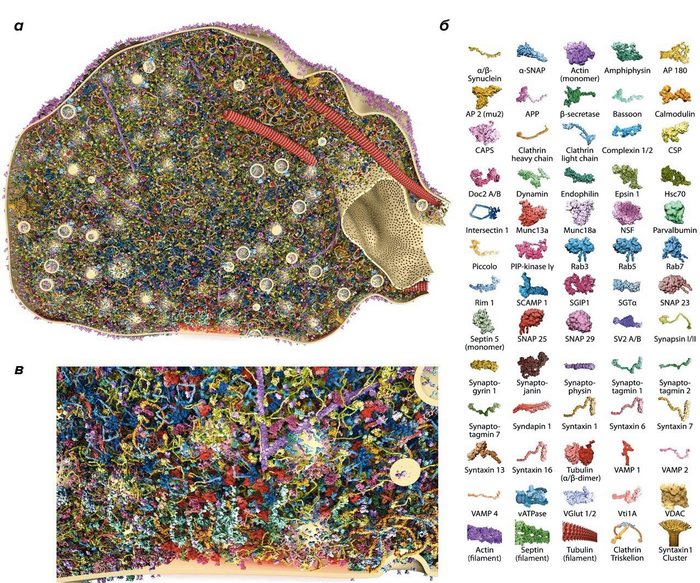
Трехмерная реконструкция синапса
а — Срез через синаптическое окончание. Изображение содержит 60 белков, которые расположены в количестве копий и местоположениях, определенных с помощью микроскопии. б — Белки, указанные на реконструкции синапса. в — Увеличенное изображение активной зоны.
Credits: B. G. Wilhelm, S. Mandad, S. Truckenbrodt, K. Krohnert, C. Schafer, et. al.. (2014). Composition of isolated synaptic boutons reveals the amounts of vesicle trafficking proteins.
Больше околонаучного на канале t.me/everScience.
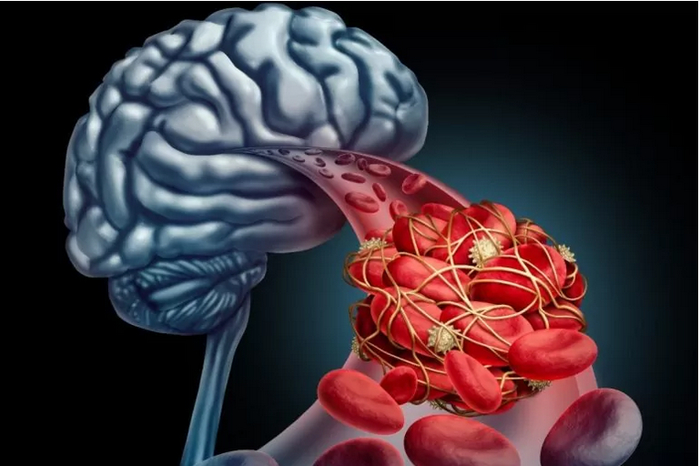
Умный мозг не только большой, но и жаждущий крови
Мозгу нужно много крови, чтобы быть умным.
Нынешняя парадигма состоит в том, что человеческий интеллект становился все более сложным, когда наш мозг становился больше. Однако австралийские и южноафриканские исследователи утверждают, что это только одна сторона медали. Их исследование показало, что увеличение притока крови к мозгу может быть связано с улучшением когнитивных функций.
Используя размеры двух отверстий в основании черепа, которые позволяют артериям проходить к мозгу, исследователи смогли подсчитать, сколько крови использовалось для прохождения через мозг у 11 видов предков гоминида, от австралопитеков до архаичных Homo sapiens. Это охватывает последние 3,5 миллиона лет.
Они обнаружили, что приток крови к мозгу непропорционально увеличивается с объемом мозга. Они выяснили, что показатель притока крови к объему мозга составляет 1.4, как сообщается в исследовании, опубликованном в Royal Society Open Science.
«Размер мозга увеличился примерно на 350% на протяжении эволюции человека, но мы обнаружили, что приток крови к мозгу увеличился на удивительные 600%», – говорит руководитель исследования, профессор Роджер Сеймур из Университета Аделаиды. «Мы полагаем, что это, возможно, связано с потребностью мозга удовлетворять все более энергичные связи между нервными клетками, которые способствовали эволюции сложного мышления и обучения. Чтобы наш мозг был таким умным, он должен постоянно получать кислород и питательные вещества из крови».
Конечно, чем более метаболически активен мозг, тем больше крови требуется, но новое исследование показывает, что кровоток и объем мозга не увеличиваются согласованно. Опять же, человеческий мозг несколько особенный в том смысле, что он также очень хорошо упакован. А именно, мозг складывается в привычной морщинистой форме ореха, что позволяет формировать больше нервных связей в меньшем объеме. Это может объяснить, почему артерии, направляющие кровь в мозг, увеличиваются в размерах непропорционально размеру мозга.
Используя отверстия в черепе, исследователи определили интенсивность мозговой активности у предков, которые жили миллионы лет назад.
«На протяжении всей эволюции развитие функции нашего мозга, по-видимому, связано с тем, что нам требуется больше времени, чтобы вырасти из детства. Это также связано с семейным сотрудничеством в охоте, защите территории и уходе за молодыми», – сказал соавтор Ваня Бозиочич. «Появление этих признаков, похоже, хорошо следует за увеличением потребности мозга в крови и энергии».
Больше околонаучного у нас на канале t.me/everScience.
Научный метод в музыке — Роман Олейников
Что такое наука и какие задачи она должна решать? Существует ли музыкальная наука и какими могут быть результаты применения научного метода в этой сфере? Что такое микрохроматика и как она может изменить музыку будущего, расширить возможности её создания и восприятия?
Об этом и не только рассказывает Роман Олейников, математик, музыкальный теоретик, соавтор канала Music Theory — Science4Music, сотрудник лаборатории биомеханических систем Института машиноведения РАН.
Реставрирую шкаф
Работа не быстрая, поэтому фото до. Нашел в нем тайник, в тайнике фото.
Интересует, что за формула на доске?
Пока ответа не нашлось.
Шкаф в СПБ. Ещё была найдена карта Казани печать старая начало 20 века.
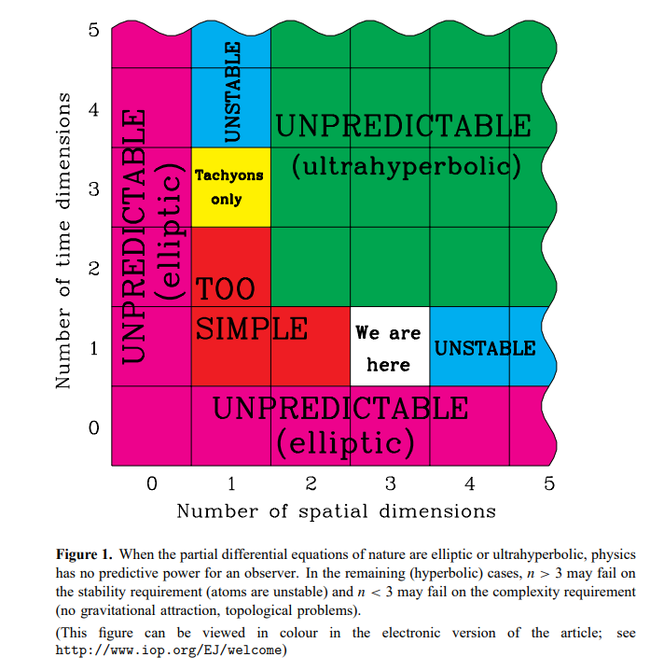
Что, если наш 4D мир станет пятимерным?
Краткая текстовая версия видео:
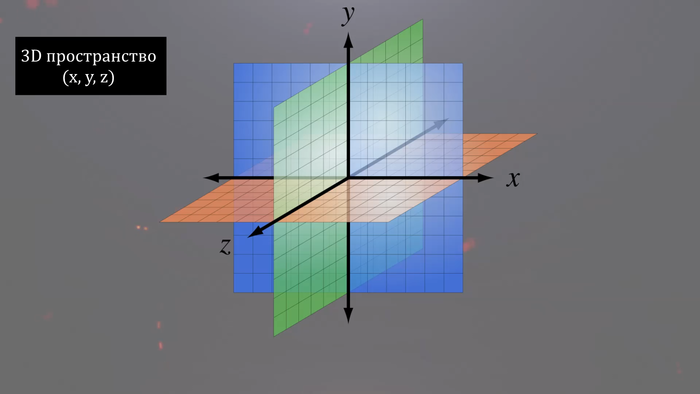
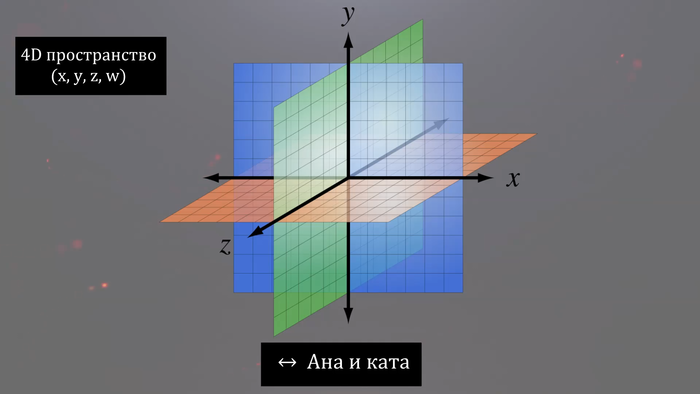
Мир, в котором мы живем, является четырехмерным. По крайней мере в макро масштабе. В нашем мире 3 пространственных измерения и одно временное. Трехмерность пространства значит, например, то, что мы можем в нем провести три взаимно перпендикулярных координатных осей расположенных под углом 90 градусов. В таком пространстве можно двигаться «влево-вправо», «вперед-назад» и «вверх-вниз».
В трехмерном пространстве мы можем завязать узел. В двумерном пространстве завязать узел невозможно. А еще в трехмерном пространстве стул может стоять только на трех ножках или больше, стул на двух ножках потеряет равновесие и упадет (Речь идет о ножках типа такого, как на фото).
А что будет, если мы добавим еще одно пространственное измерение? То есть представим себе пятимерный мир, 4 пространственных измерения и 1 временное?
В таком мире можно провести еще одну ось перпендикулярную к остальным трем осям под углом 90 градусов. В трехмерном пространстве сделать это невозможно и как-то точно визуализировать я это не могу, так что включайте фантазию.
В пятимерном мире так же добавятся новые направления движения, которые называют «ана-ката», получается: «влево-вправо», «вперед-назад», «вверх-вниз» и «ана»-«ката». Представить себе направление движения ана и ката мы не можем, так же как существо в двумерном мире не может представить себе направления вверх и вниз.
В таком мире можно завязать двумерную сферу на узел, в нашем мире сделать это невозможно, показать, соответственно, тоже нельзя. Ну и стул с тремя ножками не сможет стоять в мире с 4 пространственными измерениями, чтобы он был устойчив потребуется 4 или больше ножек.
Ну хорошо, я понимаю, вы вряд ли Вы читаете это, чтобы узнать о узлах и ножках стула, Вас интересует, что будет с нашим миром, если внезапно в него добавить еще одно измерение, вот так по щелчку пальца «тыц» и добавили еще одно пространственное измерение и вот ты уже в 5 измерении, что с тобой будет?
Если коротко то… умрешь конечно же. А еще Земля станет приплюснутой. Сейчас расскажу как именно умрешь и почему земля станет приплюснутой.
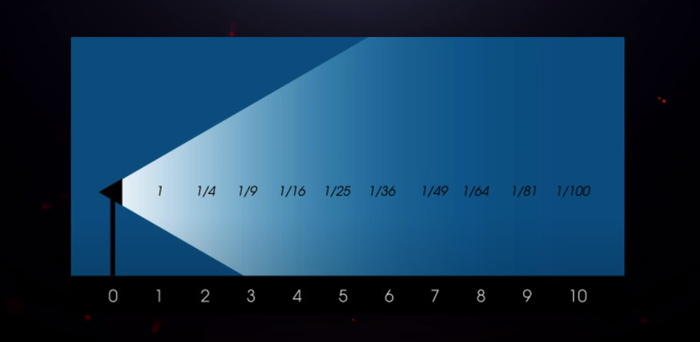
Есть такой закон – закон обратных квадратов, и он тесно связан с размерностью пространства. Возьмем для примера светящий фонарь, интенсивность света в таком случае убывает согласно закону обратных квадратов.
Объект, перемещенный на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении. На расстоянии в 3 раза большее от источника – в 9 раз меньше мощности, на расстоянии в 4 раза большее от источника – 16 раз и так далее.
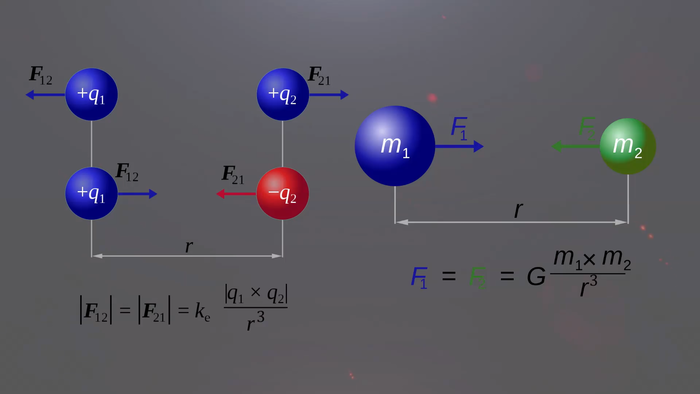
В законе всемирного тяготения сила гравитационного притяжения убывает тоже с квадратом расстояния. В два раза увеличиваем расстояние, сила притяжения уменьшается в 4 раза и так далее. Тоже самое с законом Кулона – сила притяжения или отталкивания заряженных частиц убывает с квадратом расстояния. В 5D мире закон обратных квадратов превращается в закон обратных кубов. Теперь интенсивность света будет падать не с квадратом расстояния, а с кубом расстояния. r^2 в законе Кулона и Законе всемирного тяготения превращается в r^3.
Это все полностью изменит химические элементы из которых мы состоим, некоторые атомы станут нестабильными, радиоактивными, другие наоборот, станут стабильными.
Например, в 5D мире магний был бы благородным газом, а не металлом, то есть некоторые элементы станут менее реактивными, другие более реактивными. Ионизация атомов будет осуществляться при значительно меньших энергиях, да и вообще агрегатное состояние различных элементов будет меняться не так, как в нашем мире, некоторые хим. элементы станут газообразны при комнатной температуре, некоторые затвердеют и такие вот вещи. Думаю, практически бессмысленно вспоминать биологические процессы, благодаря которым мы можем жить, ведь это все поменяется кардинально, мы мгновенно потеряем сознание и умрем, синтез белков, транспортировка различных аминокислот, нейромедиаторов, нервные импульсы, это все либо прекратится, либо изменится до неузнаваемости. Ну и конечно же спектры атомов изменятся, а это значит, что все резко поменяет цвет, что-то станет прозрачным, что-то непрозрачным, да и вообще привычные для нас источники света выглядели бы более тускло из-за r^3, с запахами та же история, правда уже некому будет смотреть и нюхать все это, ведь все живые существа погибнут.
Короче будет происходить полная жесть, что-то будет плавится, что-то превратится в газ, что-то затвердеет, некоторые вещества станут радиоактивными, привычные нам вещи потеряют свои свойства и перестанут работать так, как в нашем мире. Я напомню, что это все в мире, в котором 4 пространственных измерения и одно временное и в котором можно двигаться в направлении ана и ката. Но кроме дополнительного направления появятся также дополнительные степени свободы во вращении. В нашем мире ориентацию тела можно задать тремя углами, в быту это называется «наклон, подъём и поворот», в 5D мире надо представить себе еще 3 дополнительных степени свободы вращения перпендикулярные к 3 вышеупомянутым. Но по идее, на вращение Земли это не должно повлиять, момент импульса сохранится, ведь нужно, чтобы какая-то сила передала момент импульса Земле, чтобы она могла вращаться в какой-то непривычный для нас способ. Конечно Земля изменит свой привычный облик, из-за того, что свойства химических элементов изменятся, но из-за гравитации все должно также удерживаться вокруг центра масс, правда земля довольно быстро вращается, а так как гравитация в 5D мире у нас ослабевает с кубом расстояния, то земля сплюснется и формой будет напоминать что-то типа такого, как на картинке.
Но вообще, появится дополнительное направление, в котором могут двигаться частицы из которых состоит земля, планета начнет превращаться в гиперсферу, представить себе этот процесс, эти метаморфозы которые будут происходить, очень сложно.
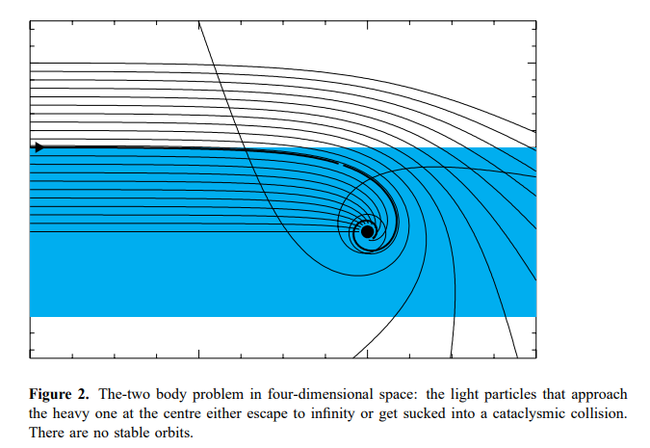
Будут ли происходить термоядерные реакции на солнце, тут под вопросом, но изменения явно произойдут. Но вот что забавно – в пятимерном мире нет стабильных орбит. Вот, посмотрите на график, это моделирование классической задачи двух тел, оказывается, что устойчивых орбит в 5D мире нет, тела либо падают друг на друга, либо улетают в бесконечность, поэтому солнечная система, как и все другие системы, разрушится, некоторые тела упадут на другие тела, а некоторые улетят бороздить просторы галактики.
Казалось бы, следуя логике как с законом обратных квадратов, все квадраты в других уравнениях тоже надо заменить на кубы и получается, что формула эквивалентности массы и энергии в пятимерном пространстве будет работать как Е=мс в кубе, но нет, эта формула, как и множество других, не изменятся в пятимерном пространстве, она, как и множество других формул, не зависит от размерности пространства.
Но даже и без этого всего, мир в 5 мерном пространстве изменится настолько, что в нем не сможет существовать жизнь в том виде, в котором существует в четырехмерном пространстве. Вообще, оказывается, четырехмерный мир – самый простой из возможных и одновременно самый оптимальный для существования в нем жизни, стабильных орбит и химии, какой мы ее знаем.
Тут есть лимит для изображений в статье, но если что — в видео рассказываю все немного более детально (вспоминаю Интерстеллар, возможности 5D существа в 4D мире, простой и необычный способ попытаться представить себе фигуру 4D и тд.) плюс стараюсь все визуализировать. По этой теме (5D измерение) написано много бреда в интернете, но проведя пару дней поиска, среди масс откровенной ахинеи удалось найти статьи ученых и математиков на эту тему, вот, собственно, сами источники:
Книга Кипа Торна, «Интерстеллар. Наука за кадром»
Источник

 masterok
masterok