ТИПЫ ШКАЛ
Психологическое измерение
2. Виды психологических измерений.
2. Нольмерное шкалирование.
3. Одномерное шкалирование.
4. Многомерное шкалирование.
Гусев, Балин, Дружинин
ТИПЫ ШКАЛ
Шкалирование — это совокупность экспериментальных и математических приемов для измерения особенностей психических процессов и состояний. Понятие «шкалирование» рассматривают в качестве синонима понятия «измерение». Под шкалированием психологических процессов понимается процесс приравнивания к этим процессам чисел по определенным правилам, а именно таким образом, чтобы в отношениях чисел отображались отношения явлений, подлежащих измерению.
Область чисел выполняет функцию модели определенных свойств предметов и дает возможность более глубоко проникать в объективно существующие свойства и взаимосвязи.
Принято различать несколько типов шкал.
Шкалы наименований, или номинативные шкалы. Представляет собой взаимно-однозначное отображение некоторой эмпирической системы в числовой системе. Само название «шкала наименований» указывает на то, что в этом случае шкальные значения играют роль лишь названий классов эквивалентности.
Шкалы наименований подчиняются законам равенства. То есть объект А может быть равен объекту В по признаку X, так что ХА=ХВ; но по отношению к третьему объекту С по признаку X он может быть неравным: ХА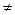 
ХС. Шкала наименований представляет собой наиболее общую форму шкал. Все типы шкал в каждом отдельном случае являются некоторыми видами шкал наименований, но обладающими при этом теми или иными дополнительными свойствами. При построении шкал наименований должны быть выполнены следующие требования: во-первых, каждый член некоторого множества объектов должен быть отнесен лишь к одному классу объектов (или к собирательному классу «прочие объекты») и, во-вторых, ни один из объектов не может быть отнесен одновременно к двум или большему числу классов. К примеру, если принять, что глаза у людей могут быть только светлыми или темными, то все люди по этому признаку разделяются на две группы.
Если делается попытка упорядочить события по признаку «мороз/оттепель», то температуры, обозначаемые как + 1° и –1°, будут входить в два разных неэквивалентных класса, в то время как температуры +1° и +10° попадут в один класс и по признаку «мороз/оттепель» будут рассматриваться как эквивалентные события.
При построении шкал наименований главными являются качественные различия, а количественные не принимаются во внимание. Поэтому числа, используемые в качестве обозначений классов эквивалентности в этих шкалах, не отражают количественных различий выраженности изучаемого признака.
В примере с температурой мы имели дело с дихотомической (делением на два класса), или альтернативной, классификацией. В случае истинной дихотомии классы могут быть четко разделены по определенному признаку, например: «мужской/ женский пол». Квазидихотомические классификации с довольно произвольными границами между классами эквивалентности, например: «способен к концентрации внимания/не способен к концентрации внимания». Первая трудность, которая при этом возникает, состоит в установлении границы классов.
В шкале наименований с числами, которые мы приписываем объектам или классам объектов, нельзя производить никаких арифметических действий. Структура шкалы остается инвариантной по отношению к перемене обозначений (наименований) и к изменению последовательности, т.е. разного рода перестановкам. Операция присвоения чисел классам объектов является совершенно произвольной. Поэтому классы объектов можно обозначать любыми символами — произвольными числами, буквами или другими знаками при одном условии: каждый символ будет использован исключительно для обозначения одного класса объектов и одновременно ни один класс объектов не будет обозначаться двумя или большим числом символов
Поскольку операции арифметического характера не допускаются, то в качестве меры центральной тенденции можно использовать лишь моду (наиболее часто встречающееся значение). Модальный класс объектов определяют после подсчета абсолютных или относительных частот, т.е. встречаемости того или иного результата в каждом классе. В качестве меры тесноты взаимосвязи между различными массивами измерений можно использовать некоторые коэффициенты корреляции. Для оценки статистической значимости различий между частотами или между модами можно использовать критерий хи-квадрат.
Шкалы порядка, или ординальные шкалы. Символы, в частности числа, присваивают классам объектов так, чтобы первые отображали не только эквивалентность или неэквивалентность, но и упорядоченность объектов в отношении измеряемого свойства. В шкалах порядка классы объектов, как и в случае шкал наименований, являются дискретными. В шкалах порядка их величины имеют лишь относительное значение. Например, если какой-то один класс объектов обозначен большим числом, чем другой, то мы понимаем, что по измеряемой характеристике первый превосходит второй, но при этом нам неизвестно, насколько велико это различие. Различия между оценками 5 — «отлично» и 4 — «хорошо» указывают лишь на то, что уровень знаний отличника выше уровня знаний «хорошиста». Однако нельзя сказать, насколько эти уровни знаний отличаются друг от друга.
Таким образом, шкала порядка отображает монотонное возрастание или убывание измеряемого признака с помощью монотонно возрастающих или монотонно уменьшающихся чисел. Оценить направление изменения признака можно только в том случае, если шкала порядка содержит не меньше трех классов, которые образуют последовательность. Из-за того, что в шкале порядка устанавливается последовательность классов, любые преобразования, связанные с перестановками элементов этой шкалы, недопустимы.
Упорядочивание объектов может быть униполярным или биполярным. При униполярном установлении порядка объекты или классы объектов соотносят, используя в качестве индикатора степень выраженности одного-единственного свойства. Например, шкала порядка для оценки умственной отсталости может содержать следующие классы: «нет отклонения от нормы/отклонение слабое/отклонение среднее/отклонение сильное».
При биполярном упорядочивании исходят, как правило, из полярных проявлений какого-то свойства, которые фиксируются в виде двух «точек отсчета» на шкале. Примером биполярной шкалы в психологическом исследовании является методика семантического дифференциала. В этом случае для построения шкалы первоначально производят отбор некоторого множества понятий, которые могут характеризовать, по мнению исследователя, изучаемые психические свойства испытуемого. Затем каждому понятию находят антоним (например: «общительный — замкнутый», «сильный — слабый», «уравновешенный — неуравновешенный»). Примерами использования в психологии порядковых шкал могут служить первичные результаты тестовых испытаний группы лиц, первичные результаты при использовании некоторых личностных опросников, работы со шкалами самооценки и т.п. Поскольку в порядковых шкалах не определена единая точка отсчета величин, то и для их элементов, как и для элементов шкал наименований, непригодны способы расчета, требующие арифметических действий, — в частности сложение и вычитание. В качестве меры положения классов объектов для преобразования шкал порядка кроме моды (Мо) могут быть использованы еще и медиана (Me), полуквартильные отклонения (Q1 и Q3), а в качестве меры тесноты взаимосвязи классов — коэффициент ранговой корреляции Ч. Спирмена (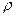 
).
Шкалы интервалов. Когда шкала обладает всеми свойствами порядковой шкалы и дополнительно к этому определены еще расстояния между ее единицами. В этих шкалах одинаковым разностям степени выраженности измеряемого свойства соответствуют равные разности между приписываемыми им числами. Шкалы интервалов имеют равные единицы измерения, однако способ их определения является произвольным, следовательно, и сами единицы произвольны. При этом неизвестна абсолютная величина отдельных значений по шкале, поскольку шкала интервалов не имеет естественной нулевой точки отсчета.
Шкалам интервалов присущи все те отношения, которые характерны для номинативных и порядковых шкал. Кроме того, для них возможно использование арифметических действий. Основными операциями с элементами интервальных шкал являются операции установления равенства, разности, сопоставление больше — меньше в отношении измеряемых свойств, а также утверждение равенства интервалов и равенства разностей между значениями одной шкалы.
При конструировании шкалы интервалов используют три произвольные операции: установление величин единиц измерения, определение нулевой точки и определение направления, в котором ведут отсчет по отношению к/нулевой точке.
Благодаря равенству единиц на уровне шкал интервалов возможна характеристика формы распределения эмпирических величин с помощью стандартных статистических показателей: средней арифметической величины (М), среднего квадратичного отклонения ( 0. Однако недопустимы (об этом часто забывают!) никакие операции прибавления или вычитания константных величин, что приводит, как было показано на примере шкал интервалов, к сдвигу точки отсчета. Дополнительно к указанным для описанных выше шкал измерения приемам статистической обработки данных для величин шкалы отношений можно рассчитывать, например, геометрические и гармонические средние, а также коэффициенты изменчивости измеряемого признака.
Считалось, что шкалы отношений не встречаются в психологических измерениях. Однако Стивенс, исходя из постулата о допустимости непосредственного измерения психических процессов, показал возможность построения шкал отношений в психофизике. Для этой цели он разработал ряд измерительных процедур, предусматривающих прямое шкалирование. Среди них наиболее известными стали методики фракционирования и мультипликации предъявляемых стимулов. К этой же группе методик можно отнести и методики оценки величин стимулов и непосредственной оценки их отношений. Общим для всех перечисленных методик прямого шкалирования является то, что в качестве измерительного инструмента выступает сам испытуемый, который оценивает количественные отношения между раздражителями.
Источник
5.1 Этапы анализа данных
В процессе подготовки и анализа данных, как правило, присутствуют следующие основные этапы:
1. Сбор первичных данных для анализа. Наблюдая и измеряя характеристики объекта, педагог-исследователь собирает первичный статистический материал. Дальнейшая задача состоит в выдвижении статистической гипотезы на основании темы и цели исследования.
2. Ввод данных в компьютер. Данные исследований необходимо ввести в компьютер и сохранить. Ввод данных может осуществляться ручным набором чисел с клавиатуры или же экспортом из файла в каком-либо формате. Введенные данные обычно отображаются в форме электронной таблицы или матрицы данных, где столбцы представляют различные переменные (рост, вес, цвет глаз), а строки – измерения значений этих переменных.
3. Преобразование данных. П роводится группировка данных, то есть распределение их на однородные группы в соответствии с интересующими исследователя признаками. Данные в каждой группе упорядочиваются — классифицируются, сортируются, структурируются, подсчитывается частота событий. Нередко также требуется удаление из введенных данных высокоамплитудных значений, которые могут быть результатом некорректных измерений или замена пропущенных (неизмеренных) значений.
4. Визуализация данных – наглядное представление данных. Для этого можно использовать как табличное представление, так и различные формы графического изображения. Человек часто намного более продуктивно и быстро воспринимает информацию в виде зрительных образов.
5. Статистический анализ — статистическая обработка полученных количественных данных, заключающаяся в вычислении некоторых статистических характеристик и оценок, позволяющих проверить нулевую гипотезу.
6. Интерпретация и представление результатов. В творчестве ученого, занимающегося проблемами педагогики, самой сложной считается задача интерпретации полученного и обработанного фактического материала. К сожалению, исследователи нередко избегают этап обсуждения фактов и переходят сразу к выводам.
Конечно, хорошо обработанные материалы, упорядоченные и оформленные в таблицы, статистические изображения могут служить базой для выводов. Однако без всестороннего обсуждения, с ходом которого должен быть ознакомлен читатель, выводы будут мало или вовсе необоснованными и неубедительными, да и сам исследователь многое теряет. Из поля его зрения выпадают ценные характеристики фактического материала, которые невидимы, то есть визуально не просматриваются, но существенно влияют на выводы.
Основная цель интерпретации — выявление и фиксирование комплекса характеристик обработанного материала, на основе которых открывается возможность обнаружить и объяснить основные тенденции и сформулировать выводы.
Отметим, что важнейшим условием объективного истолкования обработанных данных выступает научная квалификация исследователя: его эрудиция, способность к ассоциативным мыслительным действиям. Естественно, что, чем квалифицированнее в той области, где ведется поиск, исследователь, тем основательнее обсуждение и богаче его результаты.
5.2 Представление данных в наглядной форме
Большую роль при анализе данных играет владение некоторыми специальными способами представления полученных данных в наглядной — краткой и схематизированной — форме.
Табличный способ изображения данных позволяет представить качественные и количественные данные с кратким сопроводительным объясняющим текстом. Таким текстом служат название таблицы, раскрывающее связь между числовыми рядами, и внутренние заголовки таблицы (указывающие измеряемые признаки, место, время, единицы измерения и т. п.).
Матрица представляет собой разновидность таблицы со строками и рядами (столбцами), имеющими какие-либо функционально-логические связи. В результате в матрице обнаруживается наличие или отсутствие связи между различными факторам педагогического процесса.
Графики еще более наглядно, чем таблицы, отображают изменение экспериментальных данных. Графики строятся в прямоугольной системе координат, в которой на оси “X” отмечается значение выборки, а по оси “Y” — значение, порядок признака, частота события.
Композиция графика – это сочетание всех его элементов. График должен привлекать внимание, обеспечивая в то же время легкость его прочтения и усвоения. Немаловажной задачей композиции графика является художественная и эстетическая сторона его оформления.
Правила построения графиков:
1. Необходимо провести тщательный отбор из имеющегося цифрового статистического материала тех данных, которые будут изображены на графике (далеко не все полученные данные следует изображать графически).
2. Выбрать тот вид графика, который по мнению исследователя наиболее ярко будет отражать полученные данные.
3. Название графика должно быть ясным и полным, отражающим содержание и имеющим при необходимости особые пояснения.
4. Надписи и легенда располагаются, как правило, в нижней или правой части диаграммы.
5. Цифры шкалы следует наносить слева и снизу или вдоль осей. Горизонтальную шкалу (по оси абсцисс) необходимо строить слева направо, вертикальную (по оси ординат) — снизу вверх.
4. Если числовые данные не включены в диаграммы, желательно их представить рядом в табличной форме.
5. Густота координатной сетки должна быть оптимальной, не затрудняющей чтения графика.
6. Допускается количество различных цветов на графике не более трех.
7. Если графики отражают серию наблюдений, рекомендуется ясно обозначать все точки, соответствующие отдельным наблюдениям.
1. Линейный график – передает изменения в некоторых мерных числах, например, изменение средних оценок контрольных работ, проведенных в одном классе в течение учебного года.
2. Гистограмма представляет собой разновидность графика в котором по оси “Y” откладываются частотные (интервальные) значения какой-либо группировки, в результате чего график становится “ступенчатым”.
3. Полигон частот – на базе полигона частот строится гистограмма, разница между ними заключается в том, что в полигоне частота интервала сведена к его центру, а при гистограмме частоты изображают равномерно в пределах всего интервала.
4. Кумулятивный график частоты (накопляющее распределение частоты) – частота отдельных интервалов совокупности рассматривается кумулятивно, то есть к частоте каждого интервала прибавляются частоты всех предыдущих интервалов.
5. Диаграммы сопоставляют количественную информацию в виде площадей различных фигур (круг, прямоугольник, сектор, цилиндр, пузырьки и др.).
Графы — особый вид графического отображения данных результатов; это фигура, состоящая из точек (вершин), соединенных отрезками (ребрами). Вершины графа могут обозначать различные компоненты педагогического процесса, параметры, факторы, а ребра — отношения и связи между ними. Графы (как модели) часто применяются на этапе прогнозирования эксперимента, а на обобщающем этапе с ними сопоставляются результаты. Простейшим примером графа служит “дерево” целей.
Схема статистических графиков по форме графического представления
5.3 Педагогические измерения
Измерение – это процесс определения значения какого-либо признака. Значением может быть не только число, но и имя. Измерение выполняют путем непосредственного наблюдения измеряемого признака или при помощи аппаратуры.
Если в точных науках измерение сводится к сравнению данной величины с однородной ей величиной, принятой за единицу (эталоном), то для психолого-педагогических параметров таких эталонов не имеется. Более того, большинство психолого-педагогических параметров (признаки, качества, свойства, факторы) являются скрытыми (латентными), о которых можно судить лишь косвенно, по их проявлениям, т. е. весьма приближенно.
Педагогическое измерение — это операция присвоения чисел объектам и их свойствам в соответствии с определенными правилами.
Обычно измерение подразделяется на прямое и косвенное. Прямое измерение заключается в непосредственном сравнении измеряемого объекта с каким-нибудь нормативом, эталонным измерителем. В педагогических исследованиях оно встречается редко, например при определении физического развития учеников (полнота, рост).
Чаще всего используется косвенное измерение. Уровень знаний или умений учеников, их моральные качества, дисциплинированность и т. п. могут быть измерены только косвенно, на основе работы учеников, их ответов на вопросы, решения проблемных задач, числа ошибок в диктанте, на основе разных проявлений в поведении.
Задача фактиче ского измерения различных сторон педагогического явления на сегодняшний день остается неопределенной, так как в учебно-воспитательном процессе мы выделяем как педагога, так и обучаемого, которые могут описываться большим набором свойств.
5.4 Качественная и количественная информация
Основную проблему при сборе информации в психолого-педагогическом исследовании составляет количественная оценка качеств изучаемых объектов и процессов.
Психолого-педагогическая наука пока еще в основном остается описательной, эмпирической, поэтому основным видом информации в педагогическом эксперименте является качественная, содержательная.
Качеством какого-либо объекта (процесса) считаются его существенные, устойчивые свойства, благодаря которым он этим объектом и является. Таким образом, качественная информация об объекте выражает его сущность и содержание и совершенно необходима для его характеристики.
Качественными характеристиками (параметрами) описываются в педагогике все процессы и результаты обучения и воспитания, все виды деятельности, взаимоотношений участников педагогического процесса, все достижения в развитии личностей и коллективов. Основные закономерности и принципы педагогики имею качественную форму.
Количественная характеристика окружающего мира представляет более высокий уровень его познаний. Количество — это объективная определенность объекта познания, в силу которой его можно разделить на однородные части. Количественные характеристики позволяют гораздо глубже, чем описательно-логические проанализировать процессы, выявить наличие и оценить величину связи различных качеств, обнаружить закономерности.
Количество и качество тесно связаны: они диалектически взаимодополняют и превращаются друг в друга (закон перехода количества в качество). В любой качественной информации всегда содержится та или иная степень количественной.
К сожалению, проникновение в психолого-педагогическую науку и практику количественных методов затрудняется следующими обстоятельствами:
— неразработанностью и часто отсутствием адекватных методов и средств количественной оценки психолого-педагогических параметров;
— большой сложностью педагогических процессов.
5.5 Шкалирование
Шкала – это средство фиксации результатов измерения свойств объектов путем упорядочивания их в определенную числовую систему, в которой отношение между отдельными результатами выражено в соответствующих числах [1] . В процессе упорядочивания каждому элементу выборки ставится в соответствие определенный балл (шкальный индекс), устанавливающий положение наблюдаемого результата на шкале.
Шкалирование — это операция упорядочивания исходных эмпирических данных путем перевода их в шкальные оценки. Шкала дает возможность упорядочить наблюдаемые явления, при этом каждое из них получает количественную оценку (квантифицируется). Шкалирование помогает определить низшую и высшую ступени исследуемого явления.
Например, при исследовании учебных интересов учеников мы устанавливаем их границы: очень большой интерес — очень слабый интерес. Между этими границами определяется ряд ступеней. В результате складывается следующая шкала учебных интересов: очень большой интерес (1); большой интерес (2); средний (3); слабый (4); очень слабый (5). Рекомендуется вводить и экстремальные обозначения крайних границ шкалы,.
В психолого-педагогических исследованиях применяют классификацию шкал, предложенную С.Стивенсоном (см. рис. 1), согласно которой четыре основных способа измерения, связанные с различными правилами, называют измерительными шкалами (номинальная, порядковая, интервальная и шкала отношений). [2]
Рис. 1. Классификация шкал по С.Стивенсу
1. Номинальная шкала (шкала наименований), которую правильнее было бы считать классификацией, а не измерением, делит все объекты на группы по какому-либо признаку (различию). Этим признакам присваиваются определенные числа (код), что создает удобства при дальнейшей обработке экспериментальных данных. Никакого количественного соотношения между объектами в номинальной шкале нет.
Учащиеся класса делятся на две категории и обозначаются: девочки — 01, мальчики — 02.
Группы нарушителей дисциплины и их обозначение (кодирование): на уроке — 1, на улице – 2, дома — 3.
В процессе проверки соответствия подготовки выпускников школ требованиям ГОС появляется группа аттестованных и не аттестованных учеников.
2. Шкала порядка (порядковая, ранговая, ординальная) предназначена для измерения (обозначения) степени различия какого-либо признака или свойства у разных объектов. Самым ярким примером порядковой шкалы является пятибалльная система оценки ЗУН учащихся. Для нее разработаны критерии и различные методы измерения. 3начительно труднее применять порядковую шкалу для количественных оценок других качеств личности (в воспитательном процессе). Имеется несколько разновидностей порядкового шкалирования (измерения):
· ранжирование (в ряд),
· группировка (ранжирование по группам),
· метод полярных профилей.
Ранжирование. Изучаемые объекты располагаются в ряд (упорядочиваются) по степени выраженности какого-либо качества. Первое место в этом ряду занимает объект с наиболее высоким уровнем данного качества, и ему присваивается наивысший балл (числовое значение выбирается произвольно). Затем каждому объекту ранжированного ряда присваиваются более низкие оценки, соответствующие занимаемым местам.
Группировка всей совокупности объектов наблюдения в несколько рангов, достаточно ясно отличающихся друг от друга по степени измеряемого признака.
Пример: учащиеся класса согласно пятибалльной системе оценки ЗУН делятся на отличников, хорошистов и т. д.
Парное сравнение. Учащиеся сопоставляются друг с. другом (каждый с каждым) по какому-либо качеству. Если они одинаковы, то каждый получает по баллу. Если у одного этого качества больше, чем у другого, первый получает два балла, второй – 0 (как при спортивных играх по круговой системе). Суммируя полученные каждым баллы, получаем количественное выражение уровня развития данного качества у каждого учащегося (его ранг).
Рейтинг. В этом приеме оценка объекта производится путем усреднения оценочных суждений группой компетентных экспертов. Имея общие критерии оценки (в порядковой шкале, в баллах), эксперты независимо друг от друга (в устной или письменной форме) выносят свои суждения. Усредненный результат экспертной оценки является достаточно объективным и называется рейтингом.
Метод полярных профилей. Этот прием предполагает применение для оценки условной шкалы, крайними точными которой являются противоположные значения признака (например, добрый — злой, теплый — холодный и т. п.). Промежуток между полюсами делится на произвольное количество частей (баллов).
Пример. Оценка степени доверия кандидату на выборную должность дается в полярной шкале:
(Доверяю полностью) 10 – 9 – 8 – 7 – 6 – 5 – 4 – 3 – 2 – 1 (Совсем не доверяю)
3. Интервальная шкала (интервальное намерение) — это такое присвоение чисел объектам, когда определено расстояние между объектами и предусмотрена общая для всех объектов постоянная единица измерения. Иначе говоря, в интервальной шкале вводится единица и масштаб измерения. Нулевая точка шкалы выбирается произвольно.
Примеры: температурные шкалы; шкалы стандартизированного тестирования интеллекта.
Интервальная шкала – количественная. В ней возможны все арифметические действия над числами, кроме операции деления. Таким образом, в интервальной шкале нельзя определить во сколько раз один объект больше или меньше другого. Например, если ученик ответил правильно на 10 заданий, то это не означает, что он знает вдвое больше ученика, ответившего на 5 заданий теста.
4. Шкала отношений отличается от интервальной только тем, что ее нулевая точка не произвольна, а указывает на полное отсутствие измеряемого свойства. Сюда относятся и все количественные данные, получаемые пересчетом объектов какого-либо множества (число учащихся, уроков и т. п.).
Уровни измерения и математические вычисления, используемые на данных уровнях, показаны в табл. 1. Из этой таблицы видно, что переход от одного уровня к другому сопровождается расширением класса допустимых математико-статистических операций. Как следует из таблицы, наилучшей является шкала отношений, которую на сегодняшний день удалось реализовать только в рамках физических измерений.
Математические и статистические величины, вычисление которых допустимо на данном уровне
Мода, процентные частоты, доли, корреляция
Мода, медиана, квартили, коэффициент корреляции, дисперсионный анализ
Мода, медиана, квартили, коэффициент корреляции, ранговые критерии, средняя, дисперсия, стандартное отклонение, коэффициент корреляции
Все арифметические операции, все понятия и методы математической статистики
[1] Челышкова М.Б. Теория и практика конструирования педагогических тестов. – М., 2001, стр. 359
[2] Ермолаев О.Ю. Математическая статистика для психологов: Учебник/О.Ю. Ермолаев. – 2-е изд., исп. – М.: Московский психолого-социальный институт: Флинта, 2003, стр. 122 с.
Источник
