Способ шифрования по информатике

10 популярных кодов и шифров

Авторизуйтесь

10 популярных кодов и шифров

Коды и шифры — не одно и то же: в коде каждое слово заменяется другим, в то время как в шифре заменяются все символы сообщения.

В данной статье мы рассмотрим наиболее популярные способы шифрования, а следующим шагом будет изучение основ криптографии.

Стандартные шифры

Этот шифр известен многим детям. Ключ прост: каждая буква заменяется на следующую за ней в алфавите. Так, А заменяется на Б, Б — на В, и т. д. Фраза «Уйрйшоьк Рспдсбннйту» — это «Типичный Программист».

Попробуйте расшифровать сообщение:

Сумели? Напишите в комментариях, что у вас получилось.

Шифр транспонирования

В транспозиционном шифре буквы переставляются по заранее определённому правилу. Например, если каждое слово пишется задом наперед, то из hello world получается dlrow olleh. Другой пример — менять местами каждые две буквы. Таким образом, предыдущее сообщение станет eh ll wo ro dl.

Ещё можно использовать столбчатый шифр транспонирования, в котором каждый символ написан горизонтально с заданной шириной алфавита, а шифр создаётся из символов по вертикали. Пример:

Из этого способа мы получим шифр holewdlo lr. А вот столбчатая транспозиция, реализованная программно:

Азбука Морзе

В азбуке Морзе каждая буква алфавита, цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов:
Чаще всего это шифрование передаётся световыми или звуковыми сигналами.

Сможете расшифровать сообщение, используя картинку?

Шифр Цезаря

Это не один шифр, а целых 26, использующих один принцип. Так, ROT1 — лишь один из вариантов шифра Цезаря. Получателю нужно просто сообщить, какой шаг использовался при шифровании: если ROT2, тогда А заменяется на В, Б на Г и т. д.

А здесь использован шифр Цезаря с шагом 5:

Моноалфавитная замена

Коды и шифры также делятся на подгруппы. Например, ROT1, азбука Морзе, шифр Цезаря относятся к моноалфавитной замене: каждая буква заменяется на одну и только одну букву или символ. Такие шифры очень легко расшифровываются с помощью частотного анализа.

Например, наиболее часто встречающаяся буква в английском алфавите — «E». Таким образом, в тексте, зашифрованном моноалфавитным шрифтом, наиболее часто встречающейся буквой будет буква, соответствующая «E». Вторая наиболее часто встречающаяся буква — это «T», а третья — «А».

Однако этот принцип работает только для длинных сообщений. Короткие просто не содержат в себе достаточно слов.

Шифр Виженера

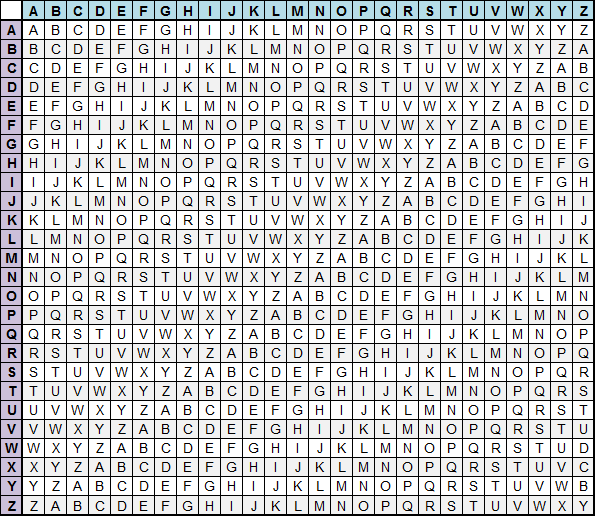
Представим, что есть таблица по типу той, что на картинке, и ключевое слово «CHAIR». Шифр Виженера использует принцип шифра Цезаря, только каждая буква меняется в соответствии с кодовым словом.

В нашем случае первая буква послания будет зашифрована согласно шифровальному алфавиту для первой буквы кодового слова «С», вторая буква — для «H», etc. Если послание длиннее кодового слова, то для (k*n+1)-ой буквы, где n — длина кодового слова, вновь будет использован алфавит для первой буквы кодового слова.

Чтобы расшифровать шифр Виженера, для начала угадывают длину кодового слова и применяют частотный анализ к каждой n-ной букве послания.

Попробуйте расшифровать эту фразу самостоятельно:

Подсказка длина кодового слова — 4.

Шифр Энигмы

Энигма — это машина, которая использовалась нацистами во времена Второй Мировой для шифрования сообщений.

Есть несколько колёс и клавиатура. На экране оператору показывалась буква, которой шифровалась соответствующая буква на клавиатуре. То, какой будет зашифрованная буква, зависело от начальной конфигурации колес.

Существовало более ста триллионов возможных комбинаций колёс, и со временем набора текста колеса сдвигались сами, так что шифр менялся на протяжении всего сообщения.

Цифровые шифры

В отличие от шифровки текста алфавитом и символами, здесь используются цифры. Рассказываем о способах и о том, как расшифровать цифровой код.

Двоичный код

Текстовые данные вполне можно хранить и передавать в двоичном коде. В этом случае по таблице символов (чаще всего ASCII) каждое простое число из предыдущего шага сопоставляется с буквой: 01100001 = 97 = «a», 01100010 = 98 = «b», etc. При этом важно соблюдение регистра.

Расшифруйте следующее сообщение, в котором использована кириллица:

Шифр A1Z26

Это простая подстановка, где каждая буква заменена её порядковым номером в алфавите. Только нижний регистр.

Попробуйте определить, что здесь написано:

Шифрование публичным ключом

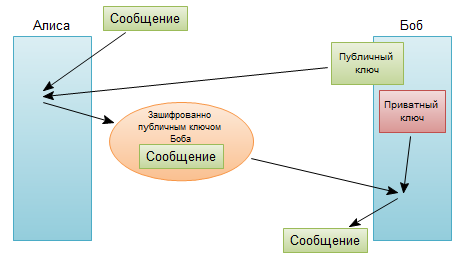
Алгоритм шифрования, применяющийся сегодня буквально во всех компьютерных системах. Есть два ключа: открытый и секретный. Открытый ключ — это большое число, имеющее только два делителя, помимо единицы и самого себя. Эти два делителя являются секретным ключом, и при перемножении дают публичный ключ. Например, публичный ключ — это 1961, а секретный — 37 и 53.

Открытый ключ используется, чтобы зашифровать сообщение, а секретный — чтобы расшифровать.

Как-то RSA выделила 1000 $ в качестве приза тому, кто найдет два пятидесятизначных делителя числа:

Как расшифровать код или шифр?

Для этого применяются специальные сервисы. Выбор такого инструмента зависит от того, что за код предстоит расшифровать. Примеры шифраторов и дешифраторов:

Источник

Элементарные шифры на понятном языке

Все мы довольно часто слышим такие слова и словосочетания, как «шифрование данных», «секретные шифры», «криптозащита», «шифрование», но далеко не все понимают, о чем конкретно идет речь. В этом посте разберемся, что из себя представляет шифрование и рассмотрим элементарные шифры с тем расчетом, чтобы даже далекие от IT люди поняли суть этого явления.

Прежде всего, разберемся в терминологии.

Шифрование – это такое преобразование исходного сообщения, которое не позволит всяким нехорошим людям прочитать данные, если они это сообщение перехватят. Делается это преобразование по специальным математическим и логическим алгоритмам, некоторые из которых мы рассмотрим ниже.

Исходное сообщение – это, собственно, то, что мы хотим зашифровать. Классический пример — текст.

Шифрованное сообщение – это сообщение, прошедшее процесс шифрования.

Шифр — это сам алгоритм, по которому мы преобразовываем сообщение.

Ключ — это компонент, на основе которого можно произвести шифрование или дешифрование.

Алфавит – это перечень всех возможных символов в исходном и зашифрованном сообщении. Включая цифры, знаки препинания, пробелы, отдельно строчные и заглавные буквы и т.д.

Теперь, когда мы говорим на более-менее одном языке, разберем простые шифры.

Шифр Атбаша

Самый-самый простой шифр. Его суть – переворот алфавита с ног на голову.

Например, есть у нас алфавит, который полностью соответствует обычной латинице.

Для реализации шифра Атбаша просто инвертируем его. «А» станет «Z», «B» превратится в «Y» и наоборот. На выходе получим такую картину:

И теперь пишем нужное сообшение на исходном алфавите и алфавите шифра

Исходное сообщение: I love habr
Зашифрованное: r olev szyi

Шифр Цезаря

Тут добавляется еще один параметр — примитивный ключ в виде числа от 1 до 25 (для латиницы). На практике, ключ будет от 4 до 10.

Опять же, для наглядности, возьмем латиницу

И теперь сместим вправо или влево каждую букву на ключевое число значений.

Например, ключ у нас будет 4 и смещение вправо.

Исходный алфавит: a b c d e f g h i j k l m n o p q r s t u v w x y z
Зашифрованный: w x y z a b c d e f g h i j k l m n o p q r s t u v

Пробуем написать сообщение:

Шифруем его и получаем следующий несвязный текст:

Шифр Вернама (XOR-шифр)

Простейший шифр на основе бинарной логики, который обладает абсолютной криптографической стойкостью. Без знания ключа, расшифровать его невозможно (доказано Клодом Шенноном).

Исходный алфавит — все та же латиница.

Сообщение разбиваем на отдельные символы и каждый символ представляем в бинарном виде.
Классики криптографии предлагают пятизначный код бодо для каждой буквы. Мы же попробуем изменить этот шифр для кодирования в 8 бит/символ на примере ASCII-таблицы. Каждую букву представим в виде бинарного кода.

Теперь вспомним курс электроники и элемент «Исключающее ИЛИ», также известный как XOR.

XOR принимает сигналы (0 или 1 каждый), проводит над ними логическую операцию и выдает один сигнал, исходя из входных значений.

Если все сигналы равны между собой (0-0 или 1-1 или 0-0-0 и т.д.), то на выходе получаем 0.
Если сигналы не равны (0-1 или 1-0 или 1-0-0 и т.д.), то на выходе получаем 1.

Теперь для шифровки сообщения, введем сам текст для шифровки и ключ такой же длины. Переведем каждую букву в ее бинарный код и выполним формулу сообщение XOR ключ

сообщение: LONDON
ключ: SYSTEM

Переведем их в бинарный код и выполним XOR:

В данном конкретном примере на месте результирующих символов мы увидим только пустое место, ведь все символы попали в первые 32 служебных символа. Однако, если перевести полученный результат в числа, то получим следующую картину:

С виду — совершенно несвязный набор чисел, но мы-то знаем.

Шифр кодового слова

Принцип шифрования примерно такой же, как у шифра цезаря. Только в этом случае мы сдвигаем алфавит не на определенное число позиций, а на кодовое слово.

Например, возьмем для разнообразия, кириллический алфавит.

Придумаем кодовое слово. Например, «Лукоморье». Выдернем из него все повторяющиеся символы. На выходе получаем слово «Лукомрье».

Теперь вписываем данное слово в начале алфавита, а остальные символы оставляем без изменений.

И теперь запишем любое сообщение и зашифруем его.

Получим в итоге следующий нечитаемый бред:

Шифр Плейфера

Классический шифр Плейфера предполагает в основе матрицу 5х5, заполненную символами латинского алфавита (i и j пишутся в одну клетку), кодовое слово и дальнейшую манипуляцию над ними.

Пусть кодовое слово у нас будет «HELLO».

Сначала поступаем как с предыдущим шифром, т.е. уберем повторы и запишем слово в начале алфавита.

Теперь возьмем любое сообщение. Например, «I LOVE HABR AND GITHUB».

Разобьем его на биграммы, т.е. на пары символов, не учитывая пробелы.

Если бы сообщение было из нечетного количества символов, или в биграмме были бы два одинаковых символа (LL, например), то на место недостающего или повторившегося символа ставится символ X.

Шифрование выполняется по нескольким несложным правилам:

1) Если символы биграммы находятся в матрице на одной строке — смещаем их вправо на одну позицию. Если символ был крайним в ряду — он становится первым.

Например, EH становится LE.

2) Если символы биграммы находятся в одном столбце, то они смещаются на одну позицию вниз. Если символ находился в самом низу столбца, то он принимает значение самого верхнего.

Например, если бы у нас была биграмма LX, то она стала бы DL.

3) Если символы не находятся ни на одной строке, ни на одном столбце, то строим прямоугольник, где наши символы — края диагонали. И меняем углы местами.

Например, биграмма RA.

По этим правилам, шифруем все сообщение.

Если убрать пробелы, то получим следующее зашифрованное сообщение:

Поздравляю. После прочтения этой статьи вы хотя бы примерно понимаете, что такое шифрование и знаете как использовать некоторые примитивные шифры и можете приступать к изучению несколько более сложных образцов шифров, о которых мы поговорим позднее.

Источник

Назначение и структура алгоритмов шифрования

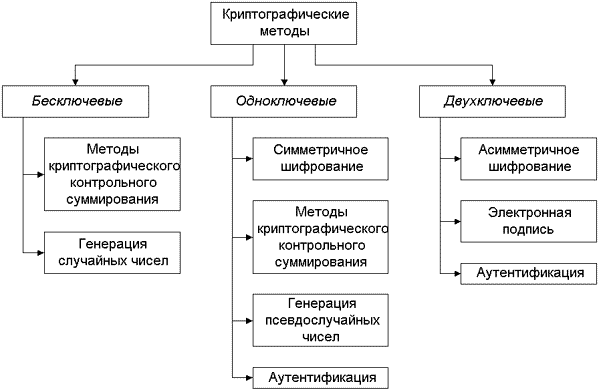
Шифрование является наиболее широко используемым криптографическим методом сохранения конфиденциальности информации, он защищает данные от несанкционированного ознакомления с ними. Для начала рассмотрим основные методы криптографической защиты информации. Словом, криптография — наука о защите информации с использованием математических методов. Существует и наука, противоположная криптографии и посвященная методам вскрытия защищенной информации — криптоанализ. Совокупность криптографии и криптоанализа принято называть криптологией. Криптографические методы могут быть классифицированы различным образом, но наиболее часто они подразделяются в зависимости от количества ключей, используемых в соответствующих криптоалгоритмах (см. рис. 1):

1. Бесключевые, в которых не используются какие-либо ключи.
2. Одноключевые — в них используется некий дополнительный ключевой параметр — обычно это секретный ключ.
3. Двухключевые, использующие в своих вычислениях два ключа: секретный и открытый.

Шифрование является основным методом защиты; рассмотрим его подробно далее.

Стоит сказать несколько слов и об остальных криптографических методах:

1. Электронная подпись используется для подтверждения целостности и авторства данных. Целостность данных означает, что данные не были случайно или преднамеренно изменены при их хранении или передаче.
   Алгоритмы электронной подписи используют два вида ключей:
   • секретный ключ используется для вычисления электронной подписи;
   • открытый ключ используется для ее проверки.

   При использовании криптографически сильного алгоритма электронной подписи и при грамотном хранении и использовании секретного ключа (то есть при невозможности использования ключа никем, кроме его владельца) никто другой не в состоянии вычислить верную электронную подпись какого-либо электронного документа.

2. Аутентификация позволяет проверить, что пользователь (или удаленный компьютер) действительно является тем, за кого он себя выдает. Простейшей схемой аутентификации является парольная — в качестве секретного элемента в ней используется пароль, который предъявляется пользователем при его проверке. Такая схема доказано является слабой, если для ее усиления не применяются специальные административно-технические меры. А на основе шифрования или хэширования (см. ниже) можно построить действительно сильные схемы аутентификации пользователей.
3. Существуют различные методы криптографического контрольного суммирования:
   • ключевое и бесключевое хэширование;
   • вычисление имитоприставок;
   • использование кодов аутентификации сообщений.

   Фактически, все эти методы различным образом из данных произвольного размера с использованием секретного ключа или без него вычисляют некую контрольную сумму фиксированного размера, однозначно соответствующую исходным данным.
   Такое криптографическое контрольное суммирование широко используется в различных методах защиты информации, например:

   • для подтверждения целостности любых данных в тех случаях, когда использование электронной подписи невозможно (например, из-за большой ресурсоемкости) или является избыточным;
   • в самих схемах электронной подписи — «подписывается» обычно хэш данных, а не все данные целиком;
   • в различных схемах аутентификации пользователей.
4. Генераторы случайных и псевдослучайных чисел позволяют создавать последовательности случайных чисел, которые широко используются в криптографии, в частности:
   • случайные числа необходимы для генерации секретных ключей, которые, в идеале, должны быть абсолютно случайными;
   • случайные числа применяются во многих алгоритмах электронной подписи;
   • случайные числа используются во многих схемах аутентификации.

   Не всегда возможно получение абсолютно случайных чисел — для этого необходимо наличие качественных аппаратных генераторов. Однако, на основе алгоритмов симметричного шифрования можно построить качественные генераторы псевдослучайных чисел.

Шифрование

Шифрование информации — это преобразование открытой информации в зашифрованную (которая чаще всего называется шифртекстом или криптограммой), и наоборот. Первая часть этого процесса называется зашифрованием, вторая — расшифрованием.

Можно представить зашифрование в виде следующей формулы:

где:
M (message) — открытая информация,
С (cipher text) — полученный в результате зашифрования шифртекст,
E (encryption) — функция зашифрования, выполняющая криптографические преобразования над M,
k1 (key) — параметр функции E, называемый ключом зашифрования.

В стандарте ГОСТ 28147-89 (стандарт определяет отечественный алгоритм симметричного шифрования) понятие ключ определено следующим образом: «Конкретное секретное состояние некоторых параметров алгоритма криптографического преобразования, обеспечивающее выбор одного преобразования из совокупности всевозможных для данного алгоритма преобразований».

Ключ может принадлежать определенному пользователю или группе пользователей и являться для них уникальным. Зашифрованная с использованием конкретного ключа информация может быть расшифрована только с использованием только этого же ключа или ключа, связанного с ним определенным соотношением.

Аналогичным образом можно представить и расшифрование:

где:
M’— сообщение, полученное в результате расшифрования,
D (decryption) — функция расшифрования; так же, как и функция зашифрования, выполняет криптографические преобразования над шифртекстом,
k2 — ключ расшифрования.

Для получения в результате расшифрования корректного открытого текста (то есть того самого, который был ранее зашифрован: M’ = M), необходимо одновременное выполнение следующих условий:

1. Функция расшифрования должна соответствовать функции зашифрования.
2. Ключ расшифрования должен соответствовать ключу зашифрования.

При отсутствии верного ключа k2 получить исходное сообщение M’ = M с помощью правильной функции D невозможно. Под словом «невозможно» в данном случае обычно понимается невозможность вычисления за реальное время при существующих вычислительных ресурсах.

Алгоритмы шифрования можно разделить на две категории (см. рис. 1):

1. Алгоритмы симметричного шифрования.
2. Алгоритмы асимметричного шифрования.

В алгоритмах симметричного шифрования для расшифрования обычно используется тот же самый ключ, что и для зашифрования, или ключ, связанный с ним каким-либо простым соотношением. Последнее встречается существенно реже, особенно в современных алгоритмах шифрования. Такой ключ (общий для зашифрования и расшифрования) обычно называется просто ключом шифрования.

В асимметричном шифровании ключ зашифрования k1 легко вычисляется из ключа k2 таким образом, что обратное вычисление невозможно. Например, соотношение ключей может быть таким:

где a и p — параметры алгоритма шифрования, имеющие достаточно большую размерность.

Такое соотношение ключей используется и в алгоритмах электронной подписи.

Основной характеристикой алгоритма шифрования является криптостойкость, которая определяет его стойкость к раскрытию методами криптоанализа. Обычно эта характеристика определяется интервалом времени, необходимым для раскрытия шифра.

Симметричное шифрование менее удобно из-за того, что при передаче зашифрованной информации кому-либо необходимо, чтобы адресат заранее получил ключ для расшифрования информации. У асимметричного шифрования такой проблемы нет (поскольку открытый ключ можно свободно передавать по сети), однако, есть свои проблемы, в частности, проблема подмены открытого ключа и медленная скорость шифрования. Наиболее часто асимметричное шифрование используется в паре с симметричным — для передачи ключа симметричного шифрования, на котором шифруется основной объем данных. Впрочем, схемы хранения и передачи ключей — это тема отдельной статьи. Здесь же позволю себе утверждать, что симметричное шифрование используется гораздо чаще асимметричного, поэтому остальная часть статьи будет посвящена только симметричному шифрованию.

Симметричное шифрование бывает двух видов:

• Блочное шифрование — информация разбивается на блоки фиксированной длины (например, 64 или 128 бит), после чего эти блоки поочередно шифруются. Причем, в различных алгоритмах шифрования или даже в разных режимах работы одного и того же алгоритма блоки могут шифроваться независимо друг от друга или «со сцеплением» — когда результат зашифрования текущего блока данных зависит от значения предыдущего блока или от результата зашифрования предыдущего блока.
• Поточное шифрование — необходимо, прежде всего, в тех случаях, когда информацию невозможно разбить на блоки — скажем, некий поток данных, каждый символ которых должен быть зашифрован и отправлен куда-либо, не дожидаясь остальных данных, достаточных для формирования блока. Поэтому алгоритмы поточного шифрования шифруют данные побитно или посимвольно. Хотя стоит сказать, что некоторые классификации не разделяют блочное и поточное шифрование, считая, что поточное шифрование — это шифрование блоков единичной длины.

Рассмотрим, как выглядят изнутри алгоритмы блочного симметричного шифрования.Структура алгоритмов шифрования

Подавляющее большинство современных алгоритмов шифрования работают весьма схожим образом: над шифруемым текстом выполняется некое преобразование с участием ключа шифрования, которое повторяется определенное число раз (раундов). При этом, по виду повторяющегося преобразования алгоритмы шифрования принято делить на несколько категорий. Здесь также существуют различные классификации, приведу одну из них. Итак, по своей структуре алгоритмы шифрования классифицируются следующим образом:

Алгоритмы на основе сети Фейстеля.

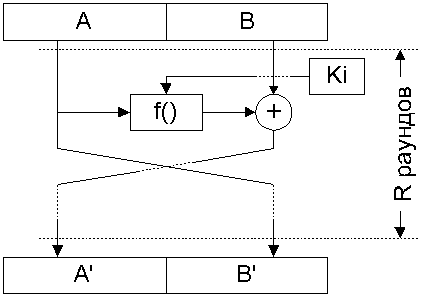
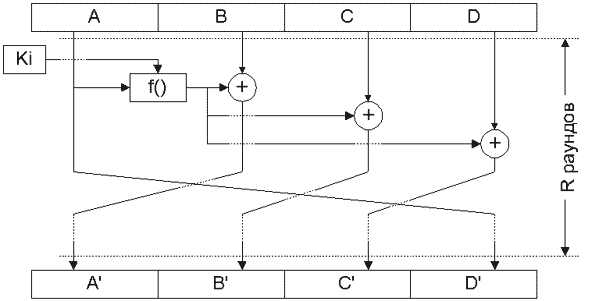
Сеть Фейстеля подразумевает разбиение обрабатываемого блока данных на несколько субблоков (чаще всего — на два), один из которых обрабатывается некоей функцией f() и накладывается на один или несколько остальных субблоков. На рис. 2 приведена наиболее часто встречающаяся структура алгоритмов на основе сети Фейстеля.

Дополнительный аргумент функции f(), обозначенный на рис. 2 как Ki, называется ключом раунда. Ключ раунда является результатом обработки ключа шифрования процедурой расширения ключа, задача которой — получение необходимого количества ключей Ki из исходного ключа шифрования относительно небольшого размера (в настоящее время достаточным для ключа симметричного шифрования считается размер 128 бит). В простейших случаях процедура расширения ключа просто разбивает ключ на несколько фрагментов, которые поочередно используются в раундах шифрования; существенно чаще процедура расширения ключа является достаточно сложной, а ключи Ki зависят от значений большинства бит исходного ключа шифрования.

Наложение обработанного субблока на необработанный чаще всего выполняется с помощью логической операции «исключающее или» — XOR (как показано на рис. 2). Достаточно часто вместо XOR здесь используется сложение по модулю 2 n , где n — размер субблока в битах. После наложения субблоки меняются местами, то есть в следующем раунде алгоритма обрабатывается уже другой субблок данных.

Такая структура алгоритмов шифрования получила свое название по имени Хорста Фейстеля (Horst Feistel) — одного из разработчиков алгоритма шифрования Lucifer и разработанного на его основе алгоритма DES (Data Encryption Standard) — бывшего (но до сих пор широко используемого) стандарта шифрования США. Оба этих алгоритма имеют структуру, аналогичную показанной на рис. 2. Среди других алгоритмов, основанных на сети Фейстеля, можно привести в пример отечественный стандарт шифрования ГОСТ 28147-89, а также другие весьма известные алгоритмы: RC5, Blowfish, TEA, CAST-128 и т.д.

На сети Фейстеля основано большинство современных алгоритмов шифрования — благодаря множеству преимуществ подобной структуры, среди которых стоит отметить следующие:

• Алгоритмы на основе сети Фейстеля могут быть сконструированы таким образом, что для зашифрования и расшифрования могут использоваться один и тот же код алгоритма — разница между этими операциями может состоять лишь в порядке применения ключей Ki; такое свойство алгоритма наиболее полезно при его аппаратной реализации или на платформах с ограниченными ресурсами; в качестве примера такого алгоритма можно привести ГОСТ 28147-89.

Алгоритмы на основе сети Фейстеля являются наиболее изученными — таким алгоритмам посвящено огромное количество криптоаналитических исследований, что является несомненным преимуществом как при разработке алгоритма, так и при его анализе.

Существует и более сложная структура сети Фейстеля, пример которой приведен на рис. 3.

Такая структура называется обобщенной или расширенной сетью Фейстеля и используется существенно реже традиционной сети Фейстеля. Примером такой сети Фейстеля может служить алгоритм RC6.
Алгоритмы на основе подстановочно-перестановочных сетей (SP-сеть — Substitution-permutation network).

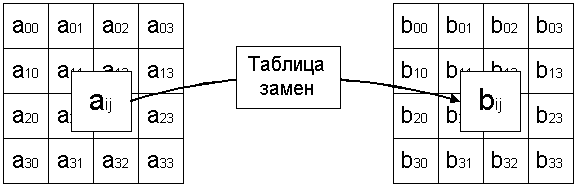
В отличие от сети Фейстеля, SP-сети обрабатывают за один раунд целиком шифруемый блок. Обработка данных сводится, в основном, к заменам (когда, например, фрагмент входного значения заменяется другим фрагментом в соответствии с таблицей замен, которая может зависеть от значения ключа Ki) и перестановкам, зависящим от ключа Ki (упрощенная схема показана на рис. 4).

Впрочем, такие операции характерны и для других видов алгоритмов шифрования, поэтому, на мой взгляд, название «подстановочно-перестановочная сеть» является достаточно условным.

SP-сети распространены существенно реже, чем сети Фейстеля; в качестве примера SP-сетей можно привести алгоритмы Serpent или SAFER+.
Алгоритмы со структурой «квадрат» (Square).

Для структуры «квадрат» характерно представление шифруемого блока данных в виде двумерного байтового массива. Криптографические преобразования могут выполняться над отдельными байтами массива, а также над его строками или столбцами.

Структура алгоритма получила свое название от алгоритма Square, который был разработан в 1996 году Винсентом Риджменом (Vincent Rijmen) и Джоан Деймен (Joan Daemen) — будущими авторами алгоритма Rijndael, ставшего новым стандартом шифрования США AES после победы на открытом конкурсе. Алгоритм Rijndael также имеет Square-подобную структуру; также в качестве примера можно привести алгоритмы Shark (более ранняя разработка Риджмена и Деймен) и Crypton. Недостатком алгоритмов со структурой «квадрат» является их недостаточная изученность, что не помешало алгоритму Rijndael стать новым стандартом США.

На рис. 5 приведен пример операции над блоком данных, выполняемой алгоритмом Rijndael.

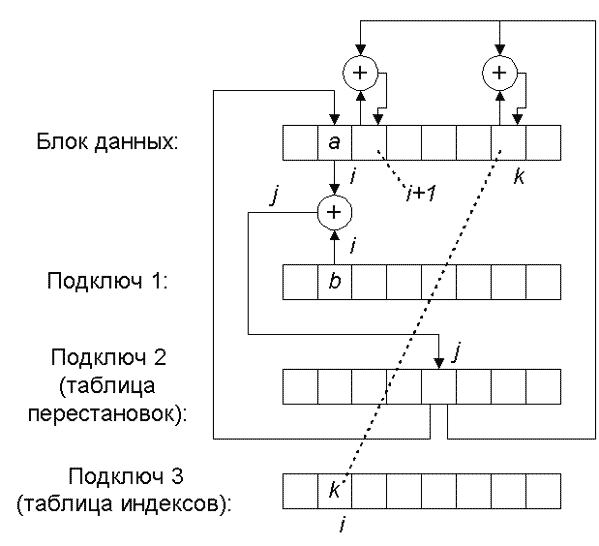
Алгоритмы с нестандартной структурой, то есть те алгоритмы, которые невозможно причислить ни к одному из перечисленных типов. Ясно, что изобретательность может быть безгранична, поэтому классифицировать все возможные варианты алгоритмов шифрования представляется сложным. В качестве примера алгоритма с нестандартной структурой можно привести уникальный по своей структуре алгоритм FROG, в каждом раунде которого по достаточно сложным правилам выполняется модификация двух байт шифруемых данных (см. рис. 6).

Строгие границы между описанными выше структурами не определены, поэтому достаточно часто встречаются алгоритмы, причисляемые различными экспертами к разным типам структур. Например, алгоритм CAST-256 относится его автором к SP-сети, а многими экспертами называется расширенной сетью Фейстеля. Другой пример — алгоритм HPC, называемый его автором сетью Фейстеля, но относимый экспертами к алгоритмам с нестандартной структурой.

Источник