Пересечение поверхностей
Из линейной алгебры (многомерной геометрии) хорошо известно, что в расширенном евклидовом пространстве Е n + размерность пересечения геометрических объектов может быть определена из соотношения
p = m 1 + m 2 — n,
где p — размерность объекта получаемого в пересечении,
m 1 — размерность первого объекта (m 1 — поверхности),
m 2 — размерность второго объекта (m 2 — поверхности),
n — размерность рассматриваемого пространства.
В соответствии с выше приведенной формулой пересечение двух поверхностей (двумерных m 1 = m 1 = 2) в трехмерном евклидовом пространстве Е 3 + должно привести к появлению одномерного объекта p = 2+2-3=1 — пространственной кривой (p = 1), все точки которой являются общими для обеих поверхностей.
При построении линии пересечения наиболее характерны два случая:
— одна из проекций линии пересечения известна и задача сводится к отысканию недостающих проекций точек по принадлежности одной из поверхностей;
— проекции линии пересечения не известны.
И в том и другом случае задача решается введением дополнительных секущих поверхностей, позволяющих находить точки, принадлежащие одновременно трем геометрическим объектам. В качестве дополнительных поверхностей берутся плоскости, цилиндры и сферы, дающие наиболее простые (заранее известные) линии при пересечении с заданными поверхностями.
Метод секущих плоскостей
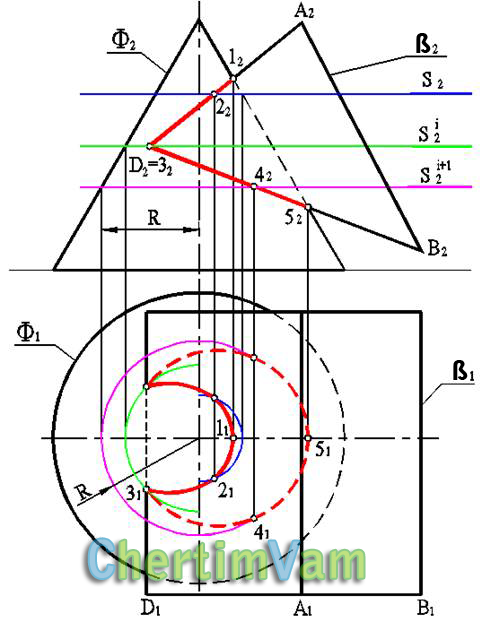
Этот метод применяют для построения линии пересечения поверхностей, позволяющих получать (одновременно) во вводимых секущих плоскостях, графически простые линии (прямые или окружности). Это утверждение может быть проиллюстрировано на примере пересечения призмы ? и конуса Ф (см. рисунок 1, Метод секущих плоскостей).
Здесь в качестве вспомогательных секущих плоскостей выступают горизонтальные плоскости уровня S i . На поверхности конуса (в силу того, что они перпендикулярны оси вращения) эти плоскости выделяют окружности, а на поверхности призмы — параллельные прямые (образующие).
Характерные точки 1, 5 линии пересечения определяют в пересечении фронтальных очерков. Текущие точки линии пересечения определятся как результат пересечения соответствующих окружностей и прямых в секущих плоскостях S i .
Метод секущих сфер
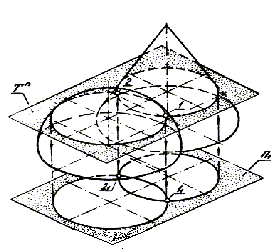
Линия пересечения двух цилиндров Ф и ? (R Ф > R ? ) может быть определена с помощью метода секущих сфер. Это определяется тем, что рассматриваемые поверхности являются поверхностями вращения и оси вращения пересекаются.
Линия пересечения распадается на две ветви, нижнюю и верхнюю, построение которых аналогично (см. рисунок 2, Метод секущих сфер).
Фронтальные проекции характерных точек линии пересечения 1 2 и 2 2 определятся в результате пересечения фронтальных очерков Ф 2 и ? 2 ,а горизонтальные — определятся по принадлежности этих точек цилиндру ?.
Низшая точка линии пересечения (3)определяется введением сферы R Ф , которая пересечет цилиндр Ф по окружности l(фронтальная проекция этой окружности совпадет с фронтальной проекцией оси вращения цилиндра ?).
С цилиндром ? эта же сфера пересечется по окружностиm. Точка 3 и есть результат пересечения окружностей lи m. Промежуточные точки определятся аналогично, как пересечение окружностей, получающихся в пересечении произвольных сфер R Ф i 2 1 2 с цилиндрами Ф и ?. Фронтальные проекции точек линии пересечения определяются как пересечения отрезков прямых, в которые вырождаются окружности, перпендикулярные оси вращения, а горизонтальные проекции находятся по принадлежности одной из поверхностей. В данном случае — поверхности ?.
Источник
Пересечение поверхностей. Метод секущих плоскостей



Пересечение поверхностей. Метод секущих сфер.
Для определения линии пересечения двух произвольных поверхностей вращения целесообразно воспользоваться одним свойством, присущим поверхностям вращения, которое состоит в том, что две любые соосные поверхности вращения пересекаются по окружностям, проходящим через точки пересечения меридианов поверхностей.
В частном случае, если одна из поверхностей вращения – сфера, приведенное выше предложение может быть сформулировано иначе: если центр секущей сферы находится на оси поверхности вращения, то сфера пересечет данную поверхность по окружностям, число которых равно числу точек пересечения главных меридианов поверхностей.
Построить линии пересечения поверхностей с помощью вспомогательных секущих сфер можно двумя способами:
1. Способом концентрических сфер;
2. Способом эксцентрических сфер.
Способ концентрических сфер.
Этот способ применяется для построения линии пересечения двух поверхностей вращения, оси которых пересекаются. Для упрощения графического решения необходимо, чтобы плоскость, определяемая осями поверхностей вращения, была параллельной какой0либо плоскости проекции.
Способ эксцентрических сфер.
Способ эксцентрических сфер может быть использован для построения линии пересечения двух поверхностей, имеющих общую плоскость симметрии. При этом каждая поверхность, имеющих общую плоскость симметрии. При этом каждая поверхность должна иметь семейство окружностей. Как и в способе концентрических сфер, плоскость симметрии должна быть параллельна одной из плоскостей проекции.
Способ эксцентрических сфер можно применять и в тех случаях, когда из пересекающихся поверхностей не является поверхностью вращения. Необходимым условием является наличие на этой поверхности семейства окружностей, которые можно рассматривать как результат пересечения поверхности со сферой. В число условий входит также условие, чтобы перпендикуляры, восстановленные из центров круговых сечений, пересекали ось поверхности вращения.
Пересечение поверхностей. Метод секущих плоскостей.
В качестве поверхностей-посредников используют секущие плоскости. Этот способ применяется в тех случаях, когда можно найти в качестве поверхностей-посредников такие плоскости, которые пересекали бы обе заданные поверхности по геометрически простым линиям — окружностям и прямым (рис. 21). Чаще всего в качестве вспомогательных секущих плоскостей выбираются плоскости уровня, то есть плоскости, параллельные плоскостям проекций. Следует отметить, что способ вспомогательных секущих плоскостей применяется во всех случаях, то есть каждая из пересекающихся поверхностей может быть как гранной, так и поверхностью вращения.
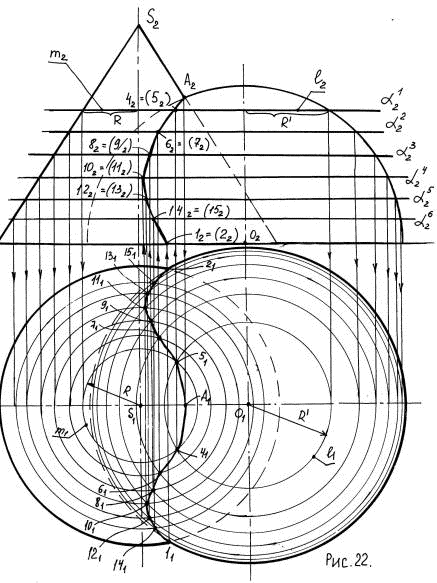
На чертеже (рис. 21, 22) прямой конус вращения пересекается с полусферой.
Построение проекций линии взаимного пересечения поверхностей осуществляется в следующей последовательности:
Определяют на чертеже положения опорных точек кривой пересечения. Фронтальная проекция A2 самой высшей точки кривой пересечения определяется на пересечении главных меридианов пересекающихся поверхностей: для конуса главным меридианом является очерковый треугольник, а для полусферы — очерковая полуокружность во фронтальной плоскости проекций.
Проведя линию связи из точки A2 до пересечения с горизонтальной проекций главных меридианов, получаем горизонтальную проекцию A1 самой высшей точки кривой пересечения. То обстоятельство, что основания фигур располагаются непосредственно в горизонтальной плоскости проекций (рис. 22) позволяет выявить положения самых низших точек 1 и 2 кривой пересечения.
Действительно, точки 11 и 21 пересечения проекций оснований фигур являются горизонтальными проекциями самых низших точек 1 и 2 кривой персечения. Их фронтальные проекции 12 и 22 располагаются на оси ОХ и определяются пересечением оси ОХ с линиями связи, проведенными из точек 11 и 21. В тоже время по отношению к наблюдателю точки 1(11;12) и 2(21;22) являются самой близкой и самой дальней точками кривой пересечения соответственно.
Все точки, кроме A, 1 и 2 являются регулярными точками кривой пересечения. Для определения на чертеже положения их проекций используют способ вспомогательных секущих плоскостей. При этом необходимо удачно выбрать положение секущей плоскости. Это положение выбирают таким образом, чтобы в сечении каждой из заданных поверхностей вращения получались графически простые линии — прямые или окружности.

В данной задаче в качестве вспомогательных секущих плоскостей выбирают горизонтальные плоскости уровня, так как они пересекают обе поверхности: конус и полусферу, по графически простым линиям — окружностям. На чертеже проводят одну секущую плоскость α1, задав ее фронтальным следом α21. Далее строят проекции параллелей — окружностей сечения секущей плоскостью α1 конуса и полусферы. На чертеже фронтальные проекции этих параллелей l2 и m2 располагаются на следе α21 секущей плоскости α1.
Горизонтальные проекции l1 и m1 этих параллелей представляют собой окружности с центрами S1 и O1, радиусами R и R′ соответственно. В пересечении горизонтальных проекций l1 и m1 параллелей получают горизонтальные проекции 41 и 51 регулярных точек кривой пересечения. Проведя линии связи из точек 41 и 51 до пересечения со следом α21 секущей плоскости α1, получают фронтальные проекции 42 и 52 кривой пересечения. Построенные точки 4(41; 42) и 5(51; 52) являются регулярными точками кривой пересечения. Аналогичным образом проводят несколько ниже секущие плоскости α2 — α6, задав их на чертеже фронтальными следами α22 — α26, и строят регулярные точки 6(61; 62) — 15(151; 152) кривой пересечения поверхностей.
После построения на чертеже проекций опорных и регулярных точек кривой соединяют их одноименные проекции плавной кривой (при помощи лекала) и получают горизонтальную и фронтальную проекции кривой взаимного пересечения заданных поверхностей. По чертежу устанавливают, что конус и полусфера имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций. Тогда горизонтальные проекции точек кривой пересечения окажутся расположенными симметрично относительно горизонтального следа главной меридианальной плоскости, являющейся общей для обеих фигур.
Фронтальные проекции точек кривой пересечения будут совпадать, так как в этом случае они являются конкурирующими по отношению к фронтальной плоскости проекций. Причем проекции точек, расположенных перед главной меридианальной плоскостью фигур, будут видимыми на фронтальной плоскости проекций, а расположенных за ней — невидимыми. Горизонтальные проекции точек кривой пересечения являются видимыми, поэтому горизонтальная проекция кривой пересечения проводится на чертеже сплошной линией.
В заключение отметим, что способ вспомогательных секущих плоскостей уровня используется тогда, когда оси вращения обеих поверхностей (если обе поверхности являются поверхностями вращения) располагаются перпендикулярно одной из плоскостей проекций.
В том случае, когда при пересечении обеих поверхностей одной секущей плоскостью невозможно получить в сечениях графически простые линии — прямые или окружности применяется способ вспомогательных секущих сфер.
Источник
Способ секущих сфер пересечение поверхностей
При определении линии пересечения двух поверхностей вращения, при их особом взаимном расположении, не всегда рационально применять вспомогательные секущие плоскости. В некоторых случаях применяют метод вспомогательных секущих сфер – концентрических или эксцентрических.
Концентрические сферические посредники применяются при определении линии пересечения двух поверхностей вращения с пересекающимися осями.
Каждая из этих поверхностей имеет семейство окружностей, являющихся линиями сечения их концентрическими сферами. Применению метода концентрических сфер должно предшествовать такое преобразование чертежа, в результате которого оси обеих поверхностей должны быть расположены параллельно одной и той же плоскости проекций (рис.151) или одна из осей становиться проецирующей прямой, а вторая — линией уровня (рис.152).
 |  |  |  |
 | |||
 | |||
 | |||
| а) модель | б) эпюр | ||
Оси поверхностей G и Q параллельны фронтальной плоскости проекций и пересекаются в точки А (рис.151). Эта точка принимается за центр всех вспомогательных концентрических сфер. Каждая из концентрических сфер пересекает поверхности по окружностям — параллелям (а, b, c, d, n), фронтальные проекции которых являются прямыми линиями (а2, b2, c2, d2, n2). Проекции точек 12, 22, 32, 42, 52 и 62 пересечения проекций параллелей принадлежат проекции искомой линии пересечения поверхностей. Пересечение главных фронтальных меридианов поверхностей определяют положение верхней и нижней точек (7 и 8) линии.
Для точного построения линии пересечения поверхностей необходимо найти точки 9 и 10, которые определяют границу зоны видимости линии пересечения поверхностей на горизонтальной проекции. Для этой цели использовалась вспомогательная секущая плоскость b , которая пересекает поверхность Q по линии m, а поверхность G по образующим, горизонтальные проекции которых пересекаясь определяют положение искомых точек.
Соединив найденные точки 1. 10 с учетом видимости получим линию пересечения поверхностей.
Рисунок 152. Пересечение поверхностей вращения,
ось одной — горизонтально проецирующая
прямая, а второй — горизонталь
Вторым примером использования в качестве вспомогательных поверхностей посредников концентрических сфер рассмотрим при определении линии пересечения поверхностей предложенных на рисунке 152. Оси поверхностей вращения G и Q пересекаются в точки А , при этом ось поверхности Q — горизонтально проецирующая прямая, а ось поверхности G — горизонталь. Точка А принимается за центр всех вспомогательных концентрических сфер.
Точки 1 и 2 линии пересечения построены с помощью сферы радиуса R. Эта сфера пересекает поверхность Q по окружности а, а поверхность G по окружности b , которая показана только на горизонтальной проекции. Пересечение горизонтальных проекций окружностей а1 и b 1 определяют проекции 11 и 21 точек линии пересечения. Их фронтальные проекции 12 и 22 построены на а2 пересечении с линиями связи.
Для нахождения точек 5 и 6 определяющих границу зоны видимости на горизонтальной проекции, использовалась вспомогательная секущая плоскость b , которая пересекает поверхность Q по окружность n, а коническую поверхность G по треугольнику, определяющему ее очерк на горизонтальной проекции.
Точки 7 и 8 находятся на границе зоны видимости фронтальной проекции, для их нахождения используется вспомогательная секущая плоскость g .
Соединив найденные точки 1. 8 с учетом видимости получим линию пересечения поверхностей G и Q.
Эксцентрические сферические посредники применяются при определении точек линии пересечения поверхностей вращения с поверхностью несущей на себе непрерывное множество окружностей. Обе поверхности должны иметь общую плоскость симметрии. Вспомогательные эксцентрические сферы пересекаются с данными поверхностями по окружностям.
 |  |  |  |
 | |||
 | |||
 | |||
| а) модель | б) эпюр | ||
Определения линии пересечения конуса и сферы применение эксцентричных сфер, как поверхностей — посредников. Центры сфер — точки расположены на оси конуса. Сфера пересекает конус и сферу по окружностям , которые пересекаются в двух точках, принадлежащих искомой линии пересечения (рис.153а).
Верхняя и нижняя точки линии пересечения найдены с помощью вспомогательной секущей плоскости — плоскости главного фронтального меридиана, пересекающая конус и сферу по треугольнику и окружности, являющимися очерками поверхностей на фронтальной плоскости проекций.
Точки, определяющие границу зоны видимости линии пересечения на горизонтальной плоскости проекций, найдены с помощью вспомогательной секущей плоскости — горизонтальной плоскости уровня, пересекающей сферу по экватору — окружности являющейся очерком шара на горизонтальной проекции, а конус по окружности — параллели.
Точки, найденные с помощью вспомогательных поверхностей посредников, определяют линию пересечения конуса и шара.
Рассмотрим, на примере определения линии пересечения конуса Q и сферы G (рис.153б), применение эксцентричных сфер, как поверхностей — посредников. Центры сфер — точки А 1 , А 2 и А 3 расположены на оси конуса. Сфера радиуса R 1 с центром в точке А 1 пересекает конус и сферу по окружностям а и в, которые пересекаются в точках 1 и 2, принадлежащих искомой линии пересечения. С помощью сферы R 2 с центром А 2 и сферы R 3 с центром А 3 определено положение точек 3, 4 и 5,6 соответственно. Точки 7 и 8 найдены с помощью вспомогательной секущей плоскости a (плоскости фронтального меридиана), пересекающей конус и сферу по главным фронтальным меридианам k и l . Точки 9 и 10, определяющие границу зоны видимости линии пересечения на горизонтальной плоскости проекций, найдены с помощью вспомогательной секущей плоскости b (горизонтальной плоскости уровня), пересекающей сферу G по экватору s, а конус Q по окружности p. Точки 1. 10, построенные с помощью вспомогательных поверхностей посредников, определяют линию пересечения конуса и шара.
Источник