Способ рыбки решение задач

Решение задач на смеси и сплавы методом Магницкого

Рассматривается применение метода Магницкого «Рыба» при решении задач на смеси и сплавы.

Просмотр содержимого документа
«Решение задач на смеси и сплавы методом Магницкого»

ЗАДАЧИ НА СМЕСИ И СПЛАВЫ

«Для каждого ребенка должен индивидуально

проектироваться его «коридор ближайшего развития».

Понятие «ребенок, не способный к математике»

должно потерять смысл и исчезнуть из лексикона

учителей, родителей, школьников и общества».

Концепция развития математического

образования в Российской Федерации

В 2016 году я принимала участие в региональном этапе конкурса «Учитель года Дона-2016», при подготовке конкурсного урока по теме «Проценты», урок обобщения в 11 классе, я познакомилась с методом Магницкого при решении задач на смеси и сплавы. Меня заинтересовал этот метод, так как я уже много лет применяю мнемонические приемы на своих уроках. Я уверена, что использование мнемотехники дает возможность свободного выбора усвоения нового материала и развития индивидуальных мнемических процессов.

При подготовке к ЕГЭ в 2015-2016 учебном году я познакомила своих одиннадцатиклассников с методом Магницкого.

Результаты моих выпускников по решению задачи на смеси и сплавы на ЕГЭ по математике профильного уровня показали, что 68% справились с этой задачей, по России этот показатель составил 40% (http://fipi.ru/sites/default/files/document/1476454097/matematika.pd ).

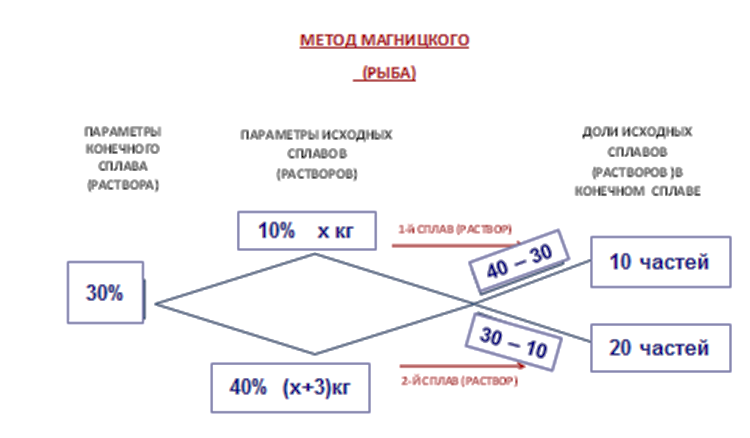
В основу метода Магницкого положено составление пропорции с помощью шаблона «Рыба».

Предлагаю рассмотреть решение задач:

Необходимо правильно внести данные в шаблон, от этого зависит успех решения задачи:

Когда «работаем» с концентрацией, то составляем разность: от большей величины вычитаем меньшую. Следующий шаг, составляем пропорцию 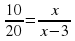и решаем ее. По условию задачи даем ответ на вопрос, выполняя необходимые вычисления.

В данной задаче неизвестна концентрация конечного продукта. Эти задачи вызывают у школьников затруднения при заполнении шаблона. Нужен дополнительный комментарий учителя, что величина концентрации полученного раствора больше концентрации данного раствора с меньшим процентным содержанием кислоты, но меньше концентрации данного раствора с большим процентным содержанием кислоты.

Составляем и решаем пропорцию: .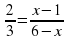

Составляем и решаем пропорцию: .

Данного вида задачи встречаются и в ОГЭ по математике в 9 классе, во II части, т.е. требуется представить развернутое решение. При оформлении решения с помощью шаблона «Рыба», не требуются «лишние» слова. В заполненной «Рыбе» видно, какая величина принята за «х», как с ней связаны остальные данные. Полученное уравнение в виде пропорции школьники решают лучше.

Задачи для самостоятельного решения:

1. В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

2. Имеется два сплава. Первый содержит 10% никеля, второй − 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

3. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 13% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

4.Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

5. Имеются два слитка, состоящие из цинка, меди и олова. Известно, что первый слиток массой 150 кг содержит 40% олова, а второй массой 250 кг — 26% меди. Процентное содержание цинка в обоих слитках одинаково. Сплавив первый и второй слитки, получили сплав, в котором оказалось 30% цинка. Сколько килограммов олова содержится в полученном сплаве?

Н.А. Чупихина, МБОУ лицей №8, г. Кисловодск, Ставропольский край, «Решение задач на смеси и сплавы»

Источник

Старинный способ решения задач на смеси, сплавы и растворы (Метод рыбки)

Впервые о нем было упомянуто в первом печатном учебнике математики Леонтия Магницкого.

Данный способ применялся купцами и ремесленниками при решении различных практических задач. Но в задачниках и различных руководствах для мастеров и торговцев никаких обоснований и разъяснений не приводилось. Просто давался рецепт решения: либо рисовалась схема, либо словесно описывалась последовательность действий — поступай так и получишь ответ.

Свежие фрукты содержат 93% воды, а высушенные 16%. Сколько требуется свежих фруктов для приготовления 21кг высушенных фруктов.

Смешали 8 литров 15-процентного водного раствора некоторого вещества с 12 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

% содержания вещества	Масса раствора	Масса вещества
1 раствор	15% = 0,15	8 л	8 •0,15
2 раствор	25% = 0,25	12 л	12 • 0,25
смесь	X	8 + 12 = 20 л	20 x

Сумма масс некоторого вещества в двух первых растворах (то есть в первых двух строчках) равна массе этого вещества в полученном растворе (третья строка таблицы):

20 x = 8•0,15 + 12 •0,25

20 x = 1,2 + 3 = 4, 2

x = 4,2 : 20 = 0,21 = 21 %

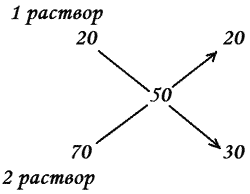
Один раствор содержит 20 % соли, а второй – 70 %. Сколько граммов первого и второго раствора нужно взять, чтобы получить 100 г 50% раствора.

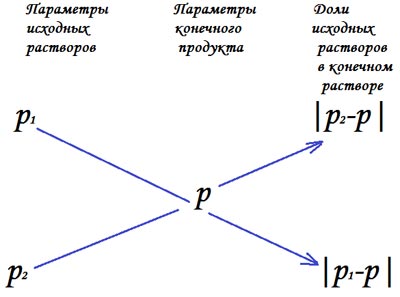
Применим правило “Метода рыбки ”.

Значит, 100 г смеси составляют 20 + 30 = 50 частей.

100 : ( 20 + 30 ) = 2 г — на 1 часть.

2 • 20 = 40 г – 20% раствора

2 • 30 = 60 г – 70 % раствора

Ответ: 40 г- 20 % раствора; 60 г- 70 % раствора.

Свежие фрукты содержат 93% воды, а высушенные – 16%. Сколько требуется свежих фруктов для приготовления 21 кг высушенных фруктов?

Решение: 93% 84%=0,84

21кг.

0,84∙21=17,64(кг), т.к Т.к. масса сухого вещества для свежих и высушенных фруктов не меняется, то 17,64:0,07=252(кг)

Если в свежих фруктах содержится 93% воды, то сухого вещества будет 100 – 93 = 7 (%), а высушенные – 16%, то сухого вещества в них будет 100 – 16 = 84 (%).

При оформлении решения задачи, можно использовать таблицу:

Общая масса, кг | Концентрация сухого вещества | Масса сухого вещества

Т.к. масса сухого вещества для свежих и высушенных фруктов не меняется, то получим уравнение:

(кг) – требуется свежих фруктов.

Решение задач с помощью приравнивания площадей равновеликих фигур.

Задача №2 Смешали 30%-й раствор соляной кислоты с 10% раствором и получили 600 г. 15%-го раствора. Сколько граммов каждого раствора надо было взять?

% 30

15

10

Х 600 m(г)

На оси х мы отмечаем массу растворов, на оси у процентное содержание растворов. Находим площади полученных прямоугольников и приравниваем их.

В данной задаче нам неизвестна масса первого вещества. Обозначим её за хг., тогда масса второго вещества равна (600-х) г. Находим площади прямоугольников. S1=15x S2=5(600-x). Приравниваем эти площади. Решаем уравнение 15х=5(600-х). Получаем х=150 г- масса первого раствора.

Находим массу второго раствора 600-150=450г.

Ответ: 150г. 30%-го раствора и 450г. 10%-го раствора.

Дата добавления: 2021-04-15 ; просмотров: 49 ; Мы поможем в написании вашей работы!

Источник

Старинные способы решения задач на смешение веществ из книги «Арифметика» Леонтия Филипповича Магницкого

ГОУ СОШ № 000 . Москвы

Старинные способы решения

задач на смешение веществ

из книги «Арифметика» Леонтия Филипповича Магницкого.

ПРОЕКТНАЯ РАБОТА ПО МАТЕМАТИКЕ

Автор: Левицкая Екатерина, 8 «В» класс

Руководитель: преподаватель математики

2. Леонтий Филиппович Магницкий — замечательный русский математик……..3

4. Сравнение современных методов решения задач на смешение веществ и метода Магницкого на примерах задач из жизни; простота и наглядность метода Магницкого…………………………………………………………………………………………5

5. Использование метода Магницкого в заданиях ГИА……………………………………10

На уроках математики, начиная с начальной школы, мы постоянно сталкиваемся с задачами на смешение различных веществ. С каждым годом эти задачи усложняются, но принцип их решения не меняется – мы берем одну часть за «x» и отталкиваемся от нее.

Но недавно я узнала, что раньше такие задачи можно было решать, не вводя переменные, и меня это заинтересовало.

Оказывается, такие способы подробно описаны в книге Леонтия Филипповича Магницкого. Перед тем как ознакомить вас с этими способами решения задач, я хотела бы немного рассказать об этом великом русском математике.

Леонтий Филиппович Магницкий

Леонтий Филиппович [9(19).6.1669 — 19(30).10.1739], русский математик; педагог. По некоторым сведениям, учился в Славяно-греко-латинской академии в Москве. С 1701 до конца жизни преподавал математику в Школе математических и навигацких наук. В 1703 напечатал свою «Арифметику», которая до середины 18 века была основным учебником математики в России. Благодаря научно-методическим и литературным достоинствам «Арифметика» Магницкого использовалась и после появления других книг по математике, более соответствовавших новому уровню науки. Книга Магницкого являлась скорее энциклопедией математических знаний, чем учебником арифметики, многие помещенные в ней сведения сообщались впервые в русской литературе. «Арифметика» сыграла большую роль в распространении математических знаний в России; по ней учился , называвший этот учебник «вратами учёности».

Рис. 1. Леонтий Филиппович Магницкий () — замечательный русский математик.

Задачи на смешение веществ

Такие задачи часто встречаются в жизни – в металлургии, химическом производстве, в медицине и фармакологии и даже в обычной жизни, например, кулинарии.

В металлургии такие задачи возникают, когда нужно знать состав различных сплавов, в химии – количество вещества, вступающего в реакцию, в медицине и фармакологии часто от дозы лекарственного вещества и его составляющих зависит результат лечения, а в кулинарии — вкус полученного блюда.

Обычно нам нужно узнать, как из двух растворов получить вещество нужной концентрации, что и в каких количествах добавить, какова доля каждого из составляющих веществ.

Как мы сейчас решаем такие задачи?

Одну часть берем за «X», составляем уравнения, если нужно, вводим вторую переменную, решаем и получаем нужные значения.

еще в начале восемнадцатого века, когда еще не было принято использование переменных, предложил остроумный графический метод решения таких задач.

Сравнение современных методов решения задач на смешение веществ и метода Магницкого на примерах задач из жизни; простота и наглядность метода Магницкого.

Рассмотрим метод Магницкого, который мы условно назвали «рыбкой» на примере задачи смешения масел.

Как смешать масла?

У некоторого человека были продажные масла. Одно — ценою десять гривен за ведро, а другое — шесть гривен за ведро.

Захотелось ему сделать из этих двух масел, смешав их, масло ценою семь гривен за ведро.

Вопрос: в каких пропорциях нужно смешать эти два масла?

Современный способ решения задачи.

Возьмем одну часть дешевого масла за «X». А часть дорогого масла — за «Y» и получим вот такое уравнение:

Мы получили, что масла нужно смешать в пропорции 1 к 3

Старинный способ решения задачи.

Привожу способ решения этой задачи (Рис. 2).

В центре пишем цену первого масла – 6. Под ним, отступя вниз, пишем цену второго масла. Слева, примерно посередине между верхней и нижней цифрами пишем стоимость желаемого масла. Соединяем три цифры отрезками прямых. Получаем картинку рис.2 –а.

Первую цену, поскольку она меньше цены желаемого масла, вычтем из цены смешанного масла, и результат поставим справа от второй цены по диагонали относительно первой цены. Затем из второй цены, которая больше цены желаемого масла, вычтем цену смешанного масла, а то что останется, напишем справа от первой цены по диагонали ко второй цене. Соединим точки отрезками, и получим вот такую картину – Рис. 2-б.

Затем определяем соотношение полученных справа величин между собой. Мы видим, что рядом с ценой дешевого масла стоит цифра 3, а рядом с ценой дорогого масла – цифра 1. Это означает,

что дешевого масла нужно взять втрое больше, чем дорогого, т. е. для получения масла ценою 7 гривен, нужно взять масла в пропорции 1 к 3, т. е. дешевого масла должно быть втрое больше, чем дорогого масла.

Сравнивая оба способа – современный и старинный (Магницкого), мы видим, что ответы, полученные двумя способами, идентичны, значит такой способ вполне применим к решению данной задачи на смешение веществ.

Рассмотрим другие подобные задачи.

Задача на смешение веществ в повседневной жизни.

Может ли данная методика пригодиться в современной жизни? Конечно, может, вот, например, в парикмахерской.

Однажды в парикмахерской подошел ко мне мастер с неожиданной просьбой:

— Не поможете ли нам разрешить задачу, с которой мы никак не можем справиться?

— Уж сколько раствора испортили из-за этого! – добавил другой мастер.

— В чем задача? – осведомился я.

— У нас есть два раствора перекиси водорода: 30% и 3% . Нужно получить 12 % раствор. Не поможете ли нам правильно подсчитать пропорции?

Как мы будем решать эту задачу?

Вот два способа, какими можно решить задачу.

Обозначим искомую часть 30% раствора – х, а 3% — раствора — y. Соответственно, надо получить 0,12 (х+у).

Ответ: для получения 12%-го раствора нужно взять одну часть 30% раствора и две части 3%-го раствора перекиси.

Второй способ — метод Магницкого.

В центре пишем концентрацию первого раствора – 30 %. Под ним, отступя вниз, пишем концентрацию второго раствора — 3% или 0, 03. Слева, примерно посередине между верхней и нижней цифрами пишем концентрацию желаемого раствора – 12% или 0, 2. Соединяем три цифры отрезками прямых.

Из первой концентрации, поскольку она больше желаемой, вычтем 0,12, подпишем справа от 0,03 результат 0, 18, который оказался по диагонали от 0,3. Из 0, 12 вычитаем 0, 03 и подписываем справа от 0,3 результат – 0,09, который тоже оказывается по диагонали от значения 0, 03. Соединяем все отрезками и получаем «рыбку» (рис. 3).

Соотношение полученных величин – 0, 09 и 0,018 – составляет 1 к 2, т. е. первого раствора концентрацией 30 % надо взять в 2 раза меньше, чем 3%-го раствора.

Ответы, полученные двумя методами, идентичны.

Как вы видите, способ решения без ввода переменных намного легче и нагляднее.

Использование метода Магницкого в заданиях ГИА.

Всем нам предстоит рано или поздно сдавать экзамены в форме ЕГЭ или ГИА. Вот как раз в ГИА и есть задача на смешение веществ в части C.

Вот и сама задача.

Имеется два сплава с разным содержанием золота. В первом сплаве – 35% золота, а во втором 60% , в каком отношении надо взять первый и второй сплав, чтобы получить из них новый, содержащий 40% золота.

Решим и эту задачу двумя способами.

Пусть часть первого сплава – х, а второго – у

Тогда количество золота в первом сплаве составляет 0, 35х, а во втором 0,6у. Масса нового сплава равна х+у, а кол-во золота составляет 0,4( х+у).

Ответ: для получения сплава, содержащего 40% золота из двух сплавов с содержанием 35% и 60%, нужно взять в 4 раза больше 35%-го сплава.

2 способ – метод Магницкого.

Аналогично методу рыбки, описанному выше, формируем изображение, показанное на рисунке 4.

Результат: соотношение полученных величин составляет 1 к 4, значит 35%-го сплава надо взять в 4 раза больше, чем 60%-го.

Как вы снова смогли убедиться, способ Леонтия Филипповича Магницкого проще для понимания.

Применение такого способа может помочь быстро и правильно решить эту довольно сложную задачу, а также, кто знает, может за необычность решения вам поставят дополнительные баллы!

• На представленных примерах видно, что изящный графический метод решения задач на смешение веществ не потерял своей актуальности и привлекательности на сегодняшний день. Достижения современной математики нисколько не уменьшают заслуг замечательных русских ученых, творивших несколько веков назад, о чем нельзя забывать изучающим математику в наши дни.

1. , , . Старинные занимательные задачи. Москва, «Наука», главная редакция Физико-математической литературы, 1985.

2. // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб.: 1890—1907.

3. П. Деятели отечественной истории. Биографический справочник. Москва, 1997 г.

Источник