- Теоретическая часть. Способ рядов – это метод, с помощью которого можно определить размер малых тел
- Способ рядов это определение
- Измерение размеров малых тел методом рядов
- Числовые ряды: определения, свойства, признаки сходимости, примеры, решения
- Базовые тезисы
- Особенности сходящихся рядов
- Необходимое условие для определения, является ли ряд сходящимся
- Как определить сходимость знакоположительного ряда.
- Как сравнивать ряды
- Признак Даламбера
- Радикальный признак Коши
- Интегральный признак Коши
- Признак Раабе
- Исследование на абсолютную сходимость
- Расходимость знакопеременных рядов
- Признаки для условной сходимости
- Признак Лейбница
- Признак Абеля-Дирихле
Теоретическая часть. Способ рядов – это метод, с помощью которого можно определить размер малых тел
Способ рядов – это метод, с помощью которого можно определить размер малых тел.
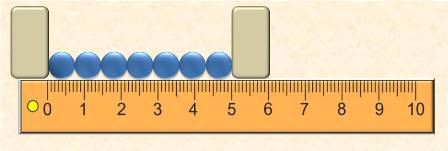
Расположите вплотную вдоль линейки n = 20 крупинок зерна. Измерьте длину ряда l и вычислите диаметр d одной крупинки:
d = l / n (см. рис. №1)


Аналогичным способом можно определить толщину листа книги. Для этого плотно сожмите книгу и измерьте ее толщину l (без учета обложки). Разделив толщину l на число листов в книге n, найдите толщину одного листа d (см. рис. №2).
Также можно определить диаметр нити или можно определить диаметр проволоки в пружине.
Для этого намотайте на карандаш вплотную, например 20 витков нити и измерьте длину навивки l. Дальше аналогично первому и второму случаю.
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)
Источник
Способ рядов это определение
1. Загадки природы и тайны быта
Вот говорят: «Толщиной с человеческий волос». А какова она – толщина волоса? Можно ли её измерить? Или, как говорят физики, оценить, в том случае, если измерения нельзя выполнить с высокой точностью. Или, допустим, можно ли измерить толщину нитки?
2. Другие х – файлы
Возможны и другие задачи. Можно ли обычной линейкой измерить:
а) толщину страницы учебника;
б) диаметр горошины или пшена;
в) толщину тонкой проволоки?
Смотрите об этом презентацию и при затруднениях читайте текст.
Не поискать ли мне тропы иной,
Приёмов новых, сочетаний странных?
«Ну, и причём здесь Шекспир?» — наверное, подумали Вы? Но …
Шекспир справедливо отметил, что когда наши познания и житейский опыт не могут решить наши проблемы, надо искать другие способы решения. Как правило, какой-нибудь метод, да и отыщется!
3. А мне это надо?
А мне это надо? – спросите Вы. Как знать? Допустим, для шитья используются нитки разной толщины. Она указывается номером на катушке. Причём нитки №10 толще, чем нитки №20.
Для изготовления некоторых элементов электрической цепи необходимо знать толщину проволоки. Для печати книг, газет и журналов используется бумага разной толщины.
А ещё надо просто научиться решать практические задачи, чтобы получать хорошие отметки и сдать экзамен по физике.
4. Истина где-то рядом
Прямые измерения размеров малых или тонких тел невозможны по той причине, что измеряемые величины соизмеримы или даже меньше цены деления используемого прибора. Одним из способов измерения размеров малых тел является, так называемый, метод рядов. Этот метод основан на принципе суммирования длин (масс, объёмов) одинаковых элементов, образующих тело в целом.
Высота стопки одинаковых книг равна сумме высот отдельных книг в этой стопке: h = n · h₀
Толщина (высота) одной книги, в этом случае, равна: h₀ = h : n
Где: n – кол-во книг; h₀ — высота одной книги.
Задача 1. Определить диаметр шарика (бусины).
Обозначим диаметр буквой d . Это и будет размером малого тела, то есть его наибольшей шириной.
Сложность этой задачи заключается в размерах тел, которые такого же порядка, как и цена деления линейки. Диаметр шариков составляет несколько миллиметров и цена деления 1 мм. Это значит, что погрешность такого измерения очень большая. В этом случае лучше применить не прямое измерение диаметра шарика, а косвенное, с использованием метода рядов.
В ряд укладываем несколько шариков. Измеряем длину ряда линейкой и делим её на количество шариков в ряду. Точность косвенных измерений диаметра шарика при таком способе будет значительно выше, чем при прямом измерении линейкой.
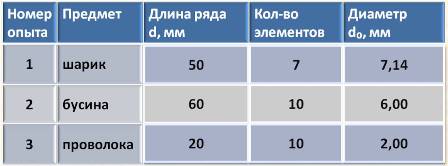
Длина ряда: l = 5 см = 50 мм Количество шариков в ряду: n = 7
Диаметр шарика: d = 50 мм: 7 = 7, 1428… мм ≈ 7, 14 мм = 7, 14 · 10 -3 м
Задача 2. Найти диаметр бусины на нитке.
В этом случае задача упрощается. Достаточно плотно сдвинуть некоторое количество бусин на нитке. Расположить этот участок нити вдоль линейки. А затем выполнить прямые и косвенные измерения.
Длина участка нити: l = 6 см = 60 мм Количество бусин: n = 10
Диаметр бусины: d = 60 мм : 10 = 6 мм = 6,0 · 10 -3 м
Задача 3. Определить диаметр тонкой проволоки.
Для решения этой задачи достаточно взять карандаш и намотать на него некоторое количество витков проволоки. Дальнейшие измерения и вычисления аналогичны.
Длина ряда из витков: l = 2 см = 20 мм Количество витков: n = 10
Диаметр (толщина) проволоки: d = 20 мм : 10 = 2 мм = 2 · 10 -3 м
Оформление результатов
Результаты измерений лучше представлять в виде таблицы. Это удобно для косвенных измерений. А также в случае проведения однотипных измерений для разных тел.
Обычно (если нет особых указаний) практические задачи выполняются с точностью до двух значащих цифр после запятой: 7,1428… мм ≈ 7,14 мм .
Результаты измерений могут быть и такого вида: 6,00 мм. Такой вид записи показывает, что вычисления также выполнены с точностью до сотых. А число либо разделилось без остатка, и дольных значений нет, либо остаток меньшего порядка (тысячные, десятитысячные и т.д.).
Окончательная запись результатов в системе СИ:
d₁ = 7,14 · 10 -3 м; d₂ = 6,00 · 10 -3 м
С учётом погрешности:
d₁ = (7,14 ± 0,07)· 10 -3 м; d₂ = (6,00 ± 0,05) · 10 -3 м.
Погрешность измерений будет уже не 0,5 мм, а в 7 (0,07 мм) и 10 (0,05 мм) раз меньше. И чем больше малых элементов в ряду, тем меньше погрешность измерений.
5. Территория экспериментов
Теперь можно решать практические задачи. В отличие от лабораторных работ, практические задачи не содержат указаний и бланк отчёта необходимо приготовить самому учащемуся. Примеры практических задач:
1. Определить толщину листа учебника физики.
2. Определить толщину нитки в катушке.
3. Определить объём одной капли воды.
Для оформления отчёта одной таблицы мало, надо знать Как составить отчёт по практической работе.
В презентации к уроку есть пример решения задачи и задание для рефлексии.
А если у Вас остались ещё вопросы – спрашивайте на форуме или на странице FQ. Или пишите на электронную почту.
Источник
Измерение размеров малых тел методом рядов
 |  |
Метод рядов используют для измерения размеров тел в случае, когда эти размеры меньше цены деления измерительного инструмента. Например, невозможно измерить толщину листа бумаги с помощью линейки с миллиметровыми делениями. Однако если измерить толщину пачки L, содержащей достаточно большое число N таких листов, и разделить полученную величину на N, то мы определим среднюю толщину листа в пачке.
При этом максимальная абсолютная погрешность ∆d измерения толщины листа в N раз меньше максимальной абсолютной погрешности ∆L прямого измерения толщины пачки ∆d = 
Данным способом можно измерить, например, диаметр тонкой проволоки, крупинок пшена и других малых тел.
 |
1. Увеличивается или уменьшается точность измерения при увеличении числа предметов в ряду?
2. Как изменится максимальная абсолютная погрешность измерения среднего диаметра тела: а) при увеличении числа тел в ряду в 10 раз; б) при уменьшении числа тел в ряду в 2 раза?
· Ознакомьтесь с критериями оценивания лабораторной работы на стр. 2-3 данного файла.
· Определите размер тел методом рядов. Проведённый эксперимент оформите в тетради для лабораторных работ в соответствии с образцом (памяткой).
Источник
Числовые ряды: определения, свойства, признаки сходимости, примеры, решения
Данная статья представляет собой структурированную и подробную информацию, которая может пригодиться во время разбора упражнений и задач. Мы рассмотрим тему числовых рядов.
Данная статья начинается с основных определений и понятий. Далее мы стандартные варианты и изучим основные формулы. Для того, чтобы закрепить материал, в статье приведены основные примеры и задачи.
Базовые тезисы
Для начала представим систему: a 1 , a 2 . . . , a n , . . . , где a k ∈ R , k = 1 , 2 . . . .
Для примера, возьмем такие числа, как: 6 , 3 , — 3 2 , 3 4 , 3 8 , — 3 16 , . . . .
Числовой ряд – это сумма членов ∑ a k k = 1 ∞ = a 1 + a 2 + . . . + a n + . . . .
Чтобы лучше понять определение, рассмотрим данный случай, в котором q = — 0 . 5 : 8 — 4 + 2 — 1 + 1 2 — 1 4 + . . . = ∑ k = 1 ∞ ( — 16 ) · — 1 2 k .
a k является общим или k –ым членом ряда.
Он выглядит примерно таким образом — 16 · — 1 2 k .
Частичная сумма ряда выглядит примерно таким образом S n = a 1 + a 2 + . . . + a n , в которой n –любое число. S n является n -ой суммой ряда.
Например, ∑ k = 1 ∞ ( — 16 ) · — 1 2 k есть S 4 = 8 — 4 + 2 — 1 = 5 .
S 1 , S 2 , . . . , S n , . . . образуют бесконечную последовательность числового ряда.
Для ряда n –ая сумму находится по формуле S n = a 1 · ( 1 — q n ) 1 — q = 8 · 1 — — 1 2 n 1 — — 1 2 = 16 3 · 1 — — 1 2 n . Используем следующую последовательность частичных сумм: 8 , 4 , 6 , 5 , . . . , 16 3 · 1 — — 1 2 n , . . . .
Ряд ∑ k = 1 ∞ a k является сходящимся тогда, когда последовательность обладает конечным пределом S = lim S n n → + ∞ . Если предела нет или последовательность бесконечна, то ряд ∑ k = 1 ∞ a k называется расходящимся.
Суммой сходящегося ряда ∑ k = 1 ∞ a k является предел последовательности ∑ k = 1 ∞ a k = lim S n n → + ∞ = S .
В данном примере lim S n n → + ∞ = lim 16 3 т → + ∞ · 1 — 1 2 n = 16 3 · lim n → + ∞ 1 — — 1 2 n = 16 3 , ряд ∑ k = 1 ∞ ( — 16 ) · — 1 2 k сходится. Сумма равна 16 3 : ∑ k = 1 ∞ ( — 16 ) · — 1 2 k = 16 3 .
В качестве примера расходящегося ряда можно привести сумму геометрической прогрессии со знаменателем большем, чем единица: 1 + 2 + 4 + 8 + . . . + 2 n — 1 + . . . = ∑ k = 1 ∞ 2 k — 1 .
n -ая частичная сумма определяется выражением S n = a 1 · ( 1 — q n ) 1 — q = 1 · ( 1 — 2 n ) 1 — 2 = 2 n — 1 , а предел частичных сумм бесконечен: lim n → + ∞ S n = lim n → + ∞ ( 2 n — 1 ) = + ∞ .
Еще одим примером расходящегося числового ряда является сумма вида ∑ k = 1 ∞ 5 = 5 + 5 + . . . . В этом случае n -ая частичная сумма может быть вычислена как S n = 5 n . Предел частичных сумм бесконечен lim n → + ∞ S n = lim n → + ∞ 5 n = + ∞ .
Сумма подобного вида как ∑ k = 1 ∞ = 1 + 1 2 + 1 3 + . . . + 1 n + . . . – это гармонический числовой ряд.
Сумма ∑ k = 1 ∞ 1 k s = 1 + 1 2 s + 1 3 s + . . . + 1 n s + . . . , где s –действительное число, является обобщенно гармоническим числовым рядом.
Определения, рассмотренные выше, помогут вам для решения большинства примеров и задач.
Для того, чтобы дополнить определения, необходимо доказать определенные уравнения.
- ∑ k = 1 ∞ 1 k – расходящийся.
Действуем методом от обратного. Если он сходится, то предел конечен. Можно записать уравнение как lim n → + ∞ S n = S и lim n → + ∞ S 2 n = S . После определенных действий мы получаем равенство l i m n → + ∞ ( S 2 n — S n ) = 0 .
S 2 n — S n = 1 + 1 2 + 1 3 + . . . + 1 n + 1 n + 1 + 1 n + 2 + . . . + 1 2 n — — 1 + 1 2 + 1 3 + . . . + 1 n = 1 n + 1 + 1 n + 2 + . . . + 1 2 n
Справедливы следующие неравенства 1 n + 1 > 1 2 n , 1 n + 1 > 1 2 n , . . . , 1 2 n — 1 > 1 2 n . Получаем, что S 2 n — S n = 1 n + 1 + 1 n + 2 + . . . + 1 2 n > 1 2 n + 1 2 n + . . . + 1 2 n = n 2 n = 1 2 . Выражение S 2 n — S n > 1 2 указывает на то, что lim n → + ∞ ( S 2 n — S n ) = 0 не достигается. Ряд расходящийся.
- b 1 + b 1 q + b 1 q 2 + . . . + b 1 q n + . . . = ∑ k = 1 ∞ b 1 q k — 1
Необходимо подтвердить, что сумма последовательности чисел сходится при q 1 , и расходится при q ≥ 1 .
Согласно приведенным выше определениям, сумма n членов определяется согласно формуле S n = b 1 · ( q n — 1 ) q — 1 .
lim n → + ∞ S n = lim n → + ∞ b 1 · q n — 1 q — 1 = b 1 · lim n → + ∞ q n q — 1 — lim n → + ∞ 1 q — 1 = = b 1 · 0 — 1 q — 1 = b 1 q — 1
Мы доказали, что числовой ряд сходится.
При q = 1 b 1 + b 1 + b 1 + . . . ∑ k = 1 ∞ b 1 . Суммы можно отыскать с использованием формулы S n = b 1 · n , предел бесконечен lim n → + ∞ S n = lim n → + ∞ b 1 · n = ∞ . В представленном варианте ряд расходится.
Если q = — 1 , то ряд выглядит как b 1 — b 1 + b 1 — . . . = ∑ k = 1 ∞ b 1 ( — 1 ) k + 1 . Частичные суммы выглядят как S n = b 1 для нечетных n , и S n = 0 для четных n . Рассмотрев данный случай, мы удостоверимся, что предела нет и ряд является расходящимся.
При q > 1 справедливо lim n → + ∞ S n = lim n → + ∞ b 1 · ( q n — 1 ) q — 1 = b 1 · lim n → + ∞ q n q — 1 — lim n → + ∞ 1 q — 1 = = b 1 · ∞ — 1 q — 1 = ∞
Мы доказали, что числовой ряд расходится.
- Ряд ∑ k = 1 ∞ 1 k s сходится, если s > 1 и расходится, если s ≤ 1 .
Для s = 1 получаем ∑ k = 1 ∞ 1 k , ряд расходится.
При s 1 получаем 1 k s ≥ 1 k для k , натурального числа. Так как ряд является расходящимся ∑ k = 1 ∞ 1 k , то предела нет. Следуя этому, последовательность ∑ k = 1 ∞ 1 k s неограниченна. Делаем вывод, что выбранный ряд расходится при s 1 .
Необходимо предоставить доказательства, что ряд ∑ k = 1 ∞ 1 k s сходится при s > 1 .
Представим S 2 n — 1 — S n — 1 :
S 2 n — 1 — S n — 1 = 1 + 1 2 s + 1 3 s + . . . + 1 ( n — 1 ) s + 1 n s + 1 ( n + 1 ) s + . . . + 1 ( 2 n — 1 ) s — — 1 + 1 2 s + 1 3 s + . . . + 1 ( n — 1 ) s = 1 n s + 1 ( n + 1 ) s + . . . + 1 ( 2 n — 1 ) s
Допустим, что 1 ( n + 1 ) s 1 n s , 1 ( n + 2 ) s 1 n s , . . . , 1 ( 2 n — 1 ) s 1 n s , тогда S 2 n — 1 — S n — 1 = 1 n s + 1 ( n + 1 ) s + . . . + 1 ( 2 n — 1 ) s 1 n s + 1 n s + . . . + 1 n s = n n s = 1 n s — 1
Представим уравнение для чисел, которые являются натуральными и четными n = 2 : S 2 n — 1 — S n — 1 = S 3 — S 1 = 1 2 s + 1 3 s 1 2 s — 1 n = 4 : S 2 n — 1 — S n — 1 = S 7 — S 3 = 1 4 s + 1 5 s + 1 6 s + 1 7 s 1 4 s — 1 = 1 2 s — 1 2 n = 8 : S 2 n — 1 — S n — 1 = S 15 — S 7 = 1 8 s + 1 9 s + . . . + 1 15 s 1 8 s — 1 = 1 2 s — 1 3 . . .
∑ k = 1 ∞ 1 k s = 1 + 1 2 s + 1 3 s + 1 4 s + . . . + 1 7 s + 1 8 s + . . . + 1 15 s + . . . = = 1 + S 3 — S 1 + S 7 — S 3 + S 15 + S 7 + . . . 1 + 1 2 s — 1 + 1 2 s — 1 2 + 1 2 s — 1 3 + . . .
Выражение 1 + 1 2 s — 1 + 1 2 s — 1 2 + 1 2 s — 1 3 + . . . – это сумма геометрической прогрессии q = 1 2 s — 1 . Согласно исходным данным при s > 1 , то 0 q 1 . Получаем, ∑ k = 1 ∞ 1 + 1 2 s — 1 + 1 2 s — 1 2 + 1 2 s — 1 3 + . . . = 1 1 — q = 1 1 — 1 2 s — 1 . Последовательность ряда при s > 1 увеличивается и ограничивается сверху 1 1 — 1 2 s — 1 . Представим, что есть предел и ряд является сходящимся ∑ k = 1 ∞ 1 k s .
Ряд ∑ k = 1 ∞ a k знакоположителен в том случае, если его члены > 0 a k > 0 , k = 1 , 2 , . . . .
Ряд ∑ k = 1 ∞ b k знакочередующийся, если знаки чисел отличаются. Данный пример представлен как ∑ k = 1 ∞ b k = ∑ k = 1 ∞ ( — 1 ) k · a k или ∑ k = 1 ∞ b k = ∑ k = 1 ∞ ( — 1 ) k + 1 · a k , где a k > 0 , k = 1 , 2 , . . . .
Ряд ∑ k = 1 ∞ b k знакопеременный, так как в нем множество чисел, отрицательных и положительных.
Второй вариант ряд – это частный случай третьего варианта.
Приведем примеры для каждого случая соответственно:
6 + 3 + 3 2 + 3 4 + 3 8 + 3 16 + . . . 6 — 3 + 3 2 — 3 4 + 3 8 — 3 16 + . . . 6 + 3 — 3 2 + 3 4 + 3 8 — 3 16 + . . .
Для третьего варианта также можно определить абсолютную и условную сходимость.
Знакочередующийся ряд ∑ k = 1 ∞ b k абсолютно сходится в том случае, когда ∑ k = 1 ∞ b k также считается сходящимся.
Подробно разберем несколько характерных вариантов
Если ряды 6 — 3 + 3 2 — 3 4 + 3 8 — 3 16 + . . . и 6 + 3 — 3 2 + 3 4 + 3 8 — 3 16 + . . . определяются как сходящиеся, то верно считать, что 6 + 3 + 3 2 + 3 4 + 3 8 + 3 16 + . . .
Знакопеременный ряд ∑ k = 1 ∞ b k считается условно сходящимся в том случае, если ∑ k = 1 ∞ b k – расходящийся, а ряд ∑ k = 1 ∞ b k считается сходящимся.
Подробно разберем вариант ∑ k = 1 ∞ ( — 1 ) k + 1 k = 1 — 1 2 + 1 3 — 1 4 + . . . . Ряд ∑ k = 1 ∞ ( — 1 ) k + 1 k = ∑ k = 1 ∞ 1 k , который состоит из абсолютных величин, определяется как расходящийся. Этот вариант считается сходящимся, так как это легко определить. Из данного примера мы узнаем, что ряд ∑ k = 1 ∞ ( — 1 ) k + 1 k = 1 — 1 2 + 1 3 — 1 4 + . . . будет считаться условно сходящимся.
Особенности сходящихся рядов
Проанализируем свойства для определенных случаев
- Если ∑ k = 1 ∞ a k будет сходится, то и ряд ∑ k = m + 1 ∞ a k также признается сходящимся. Можно отметить, что ряд без m членов также считается сходящимся. В случае, если мы добавляем к ∑ k = m + 1 ∞ a k несколько чисел, то получившийся результат также будет сходящимся.
- Если ∑ k = 1 ∞ a k сходится и сумма = S , то сходится и ряд ∑ k = 1 ∞ A · a k , ∑ k = 1 ∞ A · a k = A · S , где A –постоянная.
- Если ∑ k = 1 ∞ a k и ∑ k = 1 ∞ b k являются сходящимися , суммы A и B тоже, то и ряды ∑ k = 1 ∞ a k + b k и ∑ k = 1 ∞ a k — b k также сходятся . Суммы будут равняться A + B и A — B соответственно.
Пример 4
Определить, что ряд сходится ∑ k = 1 ∞ 2 3 k · k 3 .
Изменим выражение ∑ k = 1 ∞ 2 3 k · k 3 = ∑ k = 1 ∞ 2 3 · 1 k 4 3 . Ряд ∑ k = 1 ∞ 1 k 4 3 считается сходящимся, так как ряд ∑ k = 1 ∞ 1 k s сходится при s > 1 . В соответствии со вторым свойством, ∑ k = 1 ∞ 2 3 · 1 k 4 3 .
Определить, сходится ли ряд ∑ n = 1 ∞ 3 + n n 5 2 .
Преобразуем изначальный вариант ∑ n = 1 ∞ 3 + n n 5 2 = ∑ n = 1 ∞ 3 n 5 2 + n n 2 = ∑ n = 1 ∞ 3 n 5 2 + ∑ n = 1 ∞ 1 n 2 .
Получаем сумму ∑ n = 1 ∞ 3 n 5 2 и ∑ n = 1 ∞ 1 n 2 . Каждый ряд признается сходящимся согласно свойству. Так, как ряды сходятся, то исходный вариант тоже.
Вычислить, сходится ли ряд 1 — 6 + 1 2 — 2 + 1 4 — 2 3 + 1 8 — 2 9 + . . . и вычислить сумму.
Разложим исходный вариант:
1 — 6 + 1 2 — 2 + 1 4 — 2 3 + 1 8 — 2 9 + . . . = = 1 + 1 2 + 1 4 + 1 8 + . . . — 2 · 3 + 1 + 1 3 + 1 9 + . . . = = ∑ k = 1 ∞ 1 2 k — 1 — 2 · ∑ k = 1 ∞ 1 3 k — 2
Каждый ряд сходится, так как является одним из членов числовой последовательности. Согласно третьему свойству, мы можем вычислить, что исходный вариант также является сходящимся. Вычисляем сумму: Первый член ряда ∑ k = 1 ∞ 1 2 k — 1 = 1 , а знаменатель = 0 . 5 , за этим следует, ∑ k = 1 ∞ 1 2 k — 1 = 1 1 — 0 . 5 = 2 . Первый член ∑ k = 1 ∞ 1 3 k — 2 = 3 , а знаменатель убывающей числовой последовательности = 1 3 . Получаем: ∑ k = 1 ∞ 1 3 k — 2 = 3 1 — 1 3 = 9 2 .
Используем выражения, полученные выше, для того, чтобы определить сумму 1 — 6 + 1 2 — 2 + 1 4 — 2 3 + 1 8 — 2 9 + . . . = ∑ k = 1 ∞ 1 2 k — 1 — 2 · ∑ k = 1 ∞ 1 3 k — 2 = 2 — 2 · 9 2 = — 7
Необходимое условие для определения, является ли ряд сходящимся
Если ряд ∑ k = 1 ∞ a k является сходящимся, то предел его k -ого члена = 0 : lim k → + ∞ a k = 0 .
Если мы проверим любой вариант, то нужно не забывать о непременном условии. Если оно не выполняется, то ряд расходится. Если lim k → + ∞ a k ≠ 0 , то ряд расходящийся.
Следует уточнить, что условие важно, но не достаточно. Если равенство lim k → + ∞ a k = 0 выполняется , то это не гарантирует, что ∑ k = 1 ∞ a k является сходящимся.
Приведем пример. Для гармонического ряда ∑ k = 1 ∞ 1 k условие выполняется lim k → + ∞ 1 k = 0 , но ряд все равно расходится.
Определить сходимость ∑ n = 1 ∞ n 2 1 + n .
Проверим исходное выражение на выполнение условия lim n → + ∞ n 2 1 + n = lim n → + ∞ n 2 n 2 1 n 2 + 1 n = lim n → + ∞ 1 1 n 2 + 1 n = 1 + 0 + 0 = + ∞ ≠ 0
Предел n -ого члена не равен 0 . Мы доказали, что данный ряд расходится.
Как определить сходимость знакоположительного ряда.
Если постоянно пользоваться указанными признаками, придется постоянно вычислять пределы. Данный раздел поможет избежать сложностей во время решения примеров и задач. Для того, чтобы определить сходимость знакоположительного ряда, существует определенное условие.
Для сходимости знакоположительного ∑ k = 1 ∞ a k , a k > 0 ∀ k = 1 , 2 , 3 , . . . нужно определять ограниченную последовательность сумм.
Как сравнивать ряды
Существует несколько признаков сравнения рядов. Мы сравниваем ряд, сходимость которого предлагается определить, с тем рядом, сходимость которого известна.
Первый признак
∑ k = 1 ∞ a k и ∑ k = 1 ∞ b k — знакоположительные ряды. Неравенство a k ≤ b k справедливо для k = 1, 2, 3, . Из этого следует, что из ряда ∑ k = 1 ∞ b k мы можем получить ∑ k = 1 ∞ a k . Так как ∑ k = 1 ∞ a k расходится, то ряд ∑ k = 1 ∞ b k можно определить как расходящийся.
Данное правило постоянно используется для решения уравнений и является серьезным аргументом, которое поможет определить сходимость. Сложности могут состоять в том, что подобрать подходящий пример для сравнения можно найти далеко не в каждом случае. Довольно часто ряд выбирается по принципу, согласно которому показатель k -ого члена будет равняться результату вычитания показателей степеней числителя и знаменателя k -ого члена ряда. Допустим, что a k = k 2 + 3 4 k 2 + 5 , разность будет равна 2 – 3 = — 1 . В данном случае можно определить, что для сравнения необходим ряд с k -ым членом b k = k — 1 = 1 k , который является гармоническим.
Для того, чтобы закрепить полученный материал, детально рассмотрим пару типичных вариантов.
Определить, каким является ряд ∑ k = 1 ∞ 1 k — 1 2 .
Так как предел = 0 lim k → + ∞ 1 k — 1 2 = 0 , мы выполнили необходимое условие. Неравенство будет справедливым 1 k 1 k — 1 2 для k , которые являются натуральными. Из предыдущих пунктов мы узнали, что гармонический ряд ∑ k = 1 ∞ 1 k – расходящийся. Согласно первому признаку, можно доказать, что исходный вариант является расходящимся.
Определить, является ряд сходящимся или расходящимся ∑ k = 1 ∞ 1 k 3 + 3 k — 1 .
В данном примере выполняется необходимое условие, так как lim k → + ∞ 1 k 3 + 3 k — 1 = 0 . Представляем в виде неравенства 1 k 3 + 3 k — 1 1 k 3 для любого значения k . Ряд ∑ k = 1 ∞ 1 k 3 является сходящимся, так как гармонический ряд ∑ k = 1 ∞ 1 k s сходится при s > 1 . Согласно первому признаку, мы можем сделать вывод, что числовой ряд является сходящимся.
Определить, является каким является ряд ∑ k = 3 ∞ 1 k ln ( ln k ) . lim k → + ∞ 1 k ln ( ln k ) = 1 + ∞ + ∞ = 0 .
В данном варианте можно отметить выполнение нужного условия. Определим ряд для сравнения. Например, ∑ k = 1 ∞ 1 k s . Чтобы определить, чему равна степень, расммотрим последовательность < ln ( ln k ) >, k = 3 , 4 , 5 . . . . Члены последовательности ln ( ln 3 ) , ln ( ln 4 ) , ln ( ln 5 ) , . . . увеличивается до бесконечности. Проанализировав уравнение, можно отметить, что, взяв в качестве значения N = 1619 , то члены последовательности > 2 . Для данной последовательности будет справедливо неравенство 1 k ln ( ln k ) 1 k 2 . Ряд ∑ k = N ∞ 1 k 2 сходится согласно первому признаку, так как ряд ∑ k = 1 ∞ 1 k 2 тоже сходящийся. Отметим, что согласно первому признаку ряд ∑ k = N ∞ 1 k ln ( ln k ) сходящийся. Можно сделать вывод, что ряд ∑ k = 3 ∞ 1 k ln ( ln k ) также сходящийся.
Второй признак
Допустим, что ∑ k = 1 ∞ a k и ∑ k = 1 ∞ b k — знакоположительные числовые ряды.
Если lim k → + ∞ a k b k ≠ ∞ , то ряд ∑ k = 1 ∞ b k сходится, и ∑ k = 1 ∞ a k сходится также.
Если lim k → + ∞ a k b k ≠ 0 , то так как ряд ∑ k = 1 ∞ b k расходится, то ∑ k = 1 ∞ a k также расходится.
Если lim k → + ∞ a k b k ≠ ∞ и lim k → + ∞ a k b k ≠ 0 , то сходимость или расходимость ряда означает сходимость или расходимость другого.
Рассмотрим ∑ k = 1 ∞ 1 k 3 + 3 k — 1 с помощью второго признака. Для сравнения ∑ k = 1 ∞ b k возьмем сходящийся ряд ∑ k = 1 ∞ 1 k 3 . Определим предел: lim k → + ∞ a k b k = lim k → + ∞ 1 k 3 + 3 k — 1 1 k 3 = lim k → + ∞ k 3 k 3 + 3 k — 1 = 1
Согласно второму признаку можно определить, что сходящийся ряд ∑ k = 1 ∞ 1 k 3 означается, что первоначальный вариант также сходится.
Определить, каким является ряд ∑ n = 1 ∞ k 2 + 3 4 k 3 + 5 .
Проанализируем необходимое условие lim k → ∞ k 2 + 3 4 k 3 + 5 = 0 , которое в данном варианте выполняется. Согласно второму признаку, возьмем ряд ∑ k = 1 ∞ 1 k . Ищем предел: lim k → + ∞ k 2 + 3 4 k 3 + 5 1 k = lim k → + ∞ k 3 + 3 k 4 k 3 + 5 = 1 4
Согласно приведенным выше тезисам, расходящийся ряд влечет собой расходимость исходного ряда.
Третий признак
Рассмотрим третий признак сравнения.
Допустим, что ∑ k = 1 ∞ a k и _ ∑ k = 1 ∞ b k — знакоположительные числовые ряды. Если условие выполняется для некого номера a k + 1 a k ≤ b k + 1 b k , то сходимость данного ряда ∑ k = 1 ∞ b k означает, что ряд ∑ k = 1 ∞ a k также является сходящимся. Расходящийся ряд ∑ k = 1 ∞ a k влечет за собой расходимость ∑ k = 1 ∞ b k .
Признак Даламбера
Представим, что ∑ k = 1 ∞ a k — знакоположительный числовой ряд. Если lim k → + ∞ a k + 1 a k 1 , то ряд является сходящимся, если lim k → + ∞ a k + 1 a k > 1 , то расходящимся.
Признак Даламбера справедлив в том случае, если предел бесконечен.
Если lim k → + ∞ a k + 1 a k = — ∞ , то ряд является сходящимся, если lim k → ∞ a k + 1 a k = + ∞ , то расходящимся.
Если lim k → + ∞ a k + 1 a k = 1 , то признак Даламбера не поможет и потребуется провести еще несколько исследований.
Определить, является ряд сходящимся или расходящимся ∑ k = 1 ∞ 2 k + 1 2 k по признаку Даламбера.
Необходимо проверить, выполняется ли необходимое условие сходимости. Вычислим предел, воспользовавшись правилом Лопиталя: lim k → + ∞ 2 k + 1 2 k = » open=» ∞ ∞ = lim k → + ∞ 2 k + 1 ‘ 2 k ‘ = lim k → + ∞ 2 2 k · ln 2 = 2 + ∞ · ln 2 = 0
Мы можем увидеть, что условие выполняется. Воспользуемся признаком Даламбера: lim k → + ∞ = lim k → + ∞ 2 ( k + 1 ) + 1 2 k + 1 2 k + 1 2 k = 1 2 lim k → + ∞ 2 k + 3 2 k + 1 = 1 2 1
Ряд является сходящимся.
Определить, является ряд расходящимся ∑ k = 1 ∞ k k k ! .
Воспользуемся признаком Даламбера для того, чтобы определить рассходимость ряда: lim k → + ∞ a k + 1 a k = lim k → + ∞ ( k + 1 ) k + 1 ( k + 1 ) ! k k k ! = lim k → + ∞ ( k + 1 ) k + 1 · k ! k k · ( k + 1 ) ! = lim k → + ∞ ( k + 1 ) k + 1 k k · ( k + 1 ) = = lim k → + ∞ ( k + 1 ) k k k = lim k → + ∞ k + 1 k k = lim k → + ∞ 1 + 1 k k = e > 1
Следовательно, ряд является расходящимся.
Радикальный признак Коши
Допустим, что ∑ k = 1 ∞ a k — это знакоположительный ряд. Если lim k → + ∞ a k k 1 , то ряд является сходящимся, если lim k → + ∞ a k k > 1 , то расходящимся.
Данный признак будет считаться справедливым только в том случае, если предел бесконечен. Другими словами, если lim k → + ∞ a k k = — ∞ , то ряд сходится, если lim k → + ∞ a k k = + ∞ , то ряд расходится.
Если lim k → + ∞ a k k = 1 , то данный признак не дает никакой информации – требуется проведение дополнительного анализа.
Данный признак может быть использован в примерах, которые легко определить. Случай будет характерным тогда, когда член числового ряда – это показательно степенное выражение.
Для того, чтобы закрепить полученную информацию, рассмотрим несколько характерных примеров.
Определить, является ли знакоположительный ряд ∑ k = 1 ∞ 1 ( 2 k + 1 ) k на сходящимся.
Нужное условие считается выполненным, так как lim k → + ∞ 1 ( 2 k + 1 ) k = 1 + ∞ + ∞ = 0 .
Согласно признаку, рассмотренному выше, получаем lim k → + ∞ a k k = lim k → + ∞ 1 ( 2 k + 1 ) k k = lim k → + ∞ 1 2 k + 1 = 0 1 . Данный ряд является сходимым.
Сходится ли числовой ряд ∑ k = 1 ∞ 1 3 k · 1 + 1 k k 2 .
Используем признак, описанный в предыдущем пункте lim k → + ∞ 1 3 k · 1 + 1 k k 2 k = 1 3 · lim k → + ∞ 1 + 1 k k = e 3 1 , следовательно, числовой ряд сходится.
Интегральный признак Коши
Допустим, что ∑ k = 1 ∞ a k является знакоположительным рядом. Необходимо обозначить функцию непрерывного аргумента y = f ( x ) , которая совпадает a n = f ( n ) . Если y = f ( x ) больше нуля, не прерывается и убывает на [ a ; + ∞ ) , где a ≥ 1
, то в случае, если несобственный интеграл ∫ a + ∞ f ( x ) d x является сходящимся, то рассматриваемый ряд также сходится. Если же он расходится, то в рассматриваемом примере ряд тоже расходится.
При проверке убывания функции можно использовать материал, рассмотренный на предыдущих уроках.
Рассмотреть пример ∑ k = 2 ∞ 1 k · ln k на сходимость.
Условие сходимости ряда считается выполненным, так как lim k → + ∞ 1 k · ln k = 1 + ∞ = 0 . Рассмотрим y = 1 x · ln x . Она больше нуля, не прерывается и убывает на [ 2 ; + ∞ ) . Первые два пункта доподлинно известны, а вот на третьем следует остановиться подробнее. Находим производную: y ‘ = 1 x · ln x ‘ = x · ln x ‘ x · ln x 2 = ln x + x · 1 x x · ln x 2 = — ln x + 1 x · ln x 2 . Она меньше нуля на [ 2 ; + ∞ ) . Это доказывает тезис о том, что функция является убывающей.
Собственно, функция y = 1 x · ln x соответствует признакам принципа, который мы рассматривали выше. Воспользуемся им: ∫ 2 + ∞ d x x · ln x = lim A → + ∞ ∫ 2 A d ( ln x ) ln x = lim A → + ∞ ln ( ln x ) 2 A = = lim A → + ∞ ( ln ( ln A ) — ln ( ln 2 ) ) = ln ( ln ( + ∞ ) ) — ln ( ln 2 ) = + ∞
Согласно полученным результатам, исходный пример расходится, так как несобственный интеграл является расходящимся.
Докажите сходимость ряда ∑ k = 1 ∞ 1 ( 10 k — 9 ) ( ln ( 5 k + 8 ) ) 3 .
Так как lim k → + ∞ 1 ( 10 k — 9 ) ( ln ( 5 k + 8 ) ) 3 = 1 + ∞ = 0 , то условие считается выполненным.
Начиная с k = 4 , верное выражение 1 ( 10 k — 9 ) ( ln ( 5 k + 8 ) ) 3 1 ( 5 k + 8 ) ( ln ( 5 k + 8 ) ) 3 .
Если ряд ∑ k = 4 ∞ 1 ( 5 k + 8 ) ( ln ( 5 k + 8 ) ) 3 будет считаться сходящимся, то, согласно одному из принципов сравнения, ряд ∑ k = 4 ∞ 1 ( 10 k — 9 ) ( ln ( 5 k + 8 ) ) 3 также будет считаться сходящимся. Таким образом, мы сможет определить, что исходное выражение также является сходящимся.
Перейдем к доказательству ∑ k = 4 ∞ 1 ( 5 k + 8 ) ( ln ( 5 k + 8 ) ) 3 .
Так как функция y = 1 5 x + 8 ( ln ( 5 x + 8 ) ) 3 больше нуля, не прерывается и убывает на [ 4 ; + ∞ ) . Используем признак, описанный в предыдущем пункте:
∫ 4 + ∞ d x ( 5 x + 8 ) ( l n ( 5 x + 8 ) ) 3 = lim A → + ∞ ∫ 4 A d x ( 5 x + 8 ) ( ln ( 5 x + 8 ) ) 3 = = 1 5 · lim A → + ∞ ∫ 4 A d ( ln ( 5 x + 8 ) ( ln ( 5 x + 8 ) ) 3 = — 1 10 · lim A → + ∞ 1 ( ln ( 5 x + 8 ) ) 2 | 4 A = = — 1 10 · lim A → + ∞ 1 ( ln ( 5 · A + 8 ) ) 2 — 1 ( ln ( 5 · 4 + 8 ) ) 2 = = — 1 10 · 1 + ∞ — 1 ( ln 28 ) 2 = 1 10 · ln 28 2
В полученном сходящемся ряде, ∫ 4 + ∞ d x ( 5 x + 8 ) ( ln ( 5 x + 8 ) ) 3 , можно определить, что ∑ k = 4 ∞ 1 ( 5 k + 8 ) ( ln ( 5 k + 8 ) ) 3 также сходится.
Признак Раабе
Допустим, что ∑ k = 1 ∞ a k — знакоположительный числовой ряд.
Если lim k → + ∞ k · a k a k + 1 1 , то ряд расходится, если lim k → + ∞ k · a k a k + 1 — 1 > 1 , то сходится.
Данный способ определения можно использовать в том случае, если описанные выше техники не дают видимых результатов.
Исследование на абсолютную сходимость
Для исследования берем ∑ k = 1 ∞ b k . Используем знакоположительный ∑ k = 1 ∞ b k . Мы можем использовать любой из подходящих признаков, которые мы описывали выше. Если ряд ∑ k = 1 ∞ b k сходится, то исходный ряд является абсолютно сходящимся.
Исследовать ряд ∑ k = 1 ∞ ( — 1 ) k 3 k 3 + 2 k — 1 на сходимость ∑ k = 1 ∞ ( — 1 ) k 3 k 3 + 2 k — 1 = ∑ k = 1 ∞ 1 3 k 3 + 2 k — 1 .
Условие выполняется lim k → + ∞ 1 3 k 3 + 2 k — 1 = 1 + ∞ = 0 . Используем ∑ k = 1 ∞ 1 k 3 2 и воспользуемся вторым признаком: lim k → + ∞ 1 3 k 3 + 2 k — 1 1 k 3 2 = 1 3 .
Ряд ∑ k = 1 ∞ ( — 1 ) k 3 k 3 + 2 k — 1 сходится. Исходный ряд также абсолютно сходящийся.
Расходимость знакопеременных рядов
Если ряд ∑ k = 1 ∞ b k – расходящийся, то соответствующий знакопеременный ряд ∑ k = 1 ∞ b k либо расходящийся, либо условно сходящийся.
Лишь признак Даламбера и радикальный признак Коши помогут сделать выводы о ∑ k = 1 ∞ b k по расходимости из модулей ∑ k = 1 ∞ b k . Ряд ∑ k = 1 ∞ b k также расходится, если не выполняется необходимое условие сходимости, то есть, если lim k → ∞ + b k ≠ 0 .
Проверить расходимость 1 7 , 2 7 2 , — 6 7 3 , 24 7 4 , 120 7 5 — 720 7 6 , . . . .
Модуль k -ого члена представлен как b k = k ! 7 k .
Исследуем ряд ∑ k = 1 ∞ b k = ∑ k = 1 ∞ k ! 7 k на сходимость по признаку Даламбера: lim k → + ∞ b k + 1 b k = lim k → + ∞ ( k + 1 ) ! 7 k + 1 k ! 7 k = 1 7 · lim k → + ∞ ( k + 1 ) = + ∞ .
∑ k = 1 ∞ b k = ∑ k = 1 ∞ k ! 7 k расходится так же, как и исходный вариант.
Является ли ∑ k = 1 ∞ ( — 1 ) k · k 2 + 1 ln ( k + 1 ) сходящимся.
Рассмотрим на необходимое условие lim k → + ∞ b k = lim k → + ∞ k 2 + 1 ln ( k + 1 ) = » open=» ∞ ∞ = lim k → + ∞ = k 2 + 1 ‘ ( ln ( k + 1 ) ) ‘ = = lim k → + ∞ 2 k 1 k + 1 = lim k → + ∞ 2 k ( k + 1 ) = + ∞ . Условие не выполнено, поэтому ∑ k = 1 ∞ ( — 1 ) k · k 2 + 1 ln ( k + 1 ) ряд расходящийся. Предел был вычислен по правилу Лопиталя.
Признаки для условной сходимости
Признак Лейбница
Если величины членов знакочередующегося ряда убывают b 1 > b 2 > b 3 > . . . > . . . и предел модуля = 0 при k → + ∞ , то ряд ∑ k = 1 ∞ b k сходится.
Рассмотреть ∑ k = 1 ∞ ( — 1 ) k 2 k + 1 5 k ( k + 1 ) на сходимость.
Ряд представлен как ∑ k = 1 ∞ ( — 1 ) k 2 k + 1 5 k ( k + 1 ) = ∑ k = 1 ∞ 2 k + 1 5 k ( k + 1 ) . Нужное условие выполняется lim k → + ∞ = 2 k + 1 5 k ( k + 1 ) = 0 . Рассмотрим ∑ k = 1 ∞ 1 k по второму признаку сравнения lim k → + ∞ 2 k + 1 5 k ( k + 1 ) 1 k = lim k → + ∞ 2 k + 1 5 ( k + 1 ) = 2 5
Получаем, что ∑ k = 1 ∞ ( — 1 ) k 2 k + 1 5 k ( k + 1 ) = ∑ k = 1 ∞ 2 k + 1 5 k ( k + 1 ) расходится. Ряд ∑ k = 1 ∞ ( — 1 ) k 2 k + 1 5 k ( k + 1 ) сходится по признаку Лейбница: последовательность 2 · 1 + 1 5 · 1 · 1 1 + 1 = 3 10 , 2 · 2 + 1 5 · 2 · ( 2 + 1 ) = 5 30 , 2 · 3 + 1 5 · 3 · 3 + 1 , . . . убывает и lim k → + ∞ = 2 k + 1 5 k ( k + 1 ) = 0 .
Ряд условно сходится.
Признак Абеля-Дирихле
∑ k = 1 + ∞ u k · v k сходится в том случае, если < u k >не возрастает, а последовательность ∑ k = 1 + ∞ v k ограничена.
Исследуйте 1 — 3 2 + 2 3 + 1 4 — 3 5 + 1 3 + 1 7 — 3 8 + 2 9 + . . . на сходимость.
1 — 3 2 + 2 3 + 1 4 — 3 5 + 1 3 + 1 7 — 3 8 + 2 9 + . . . = 1 · 1 + 1 2 · ( — 3 ) + 1 3 · 2 + 1 4 · 1 + 1 5 · ( — 3 ) + 1 6 · = ∑ k = 1 ∞ u k · v k
где < u k >= 1 , 1 2 , 1 3 , . . . — невозрастающая, а последовательность < v k >= 1 , — 3 , 2 , 1 , — 3 , 2 , . . . ограничена < S k >= 1 , — 2 , 0 , 1 , — 2 , 0 , . . . . Ряд сходится.
Источник