Способ риттера как рассечь ферму

Метод Риттера теоретической механики

Вы будете перенаправлены на Автор24

В теоретической механике метод Риттера относится к разделу «статика твердого тела». Данный метод позволяет рассчитать усилия в стержнях ферм. Метод Риттера используется, в основном, для плоских систем сил.

Если необходимы расчеты усилий в ферме, можно использовать метод Риттера (если речь идет о ее стержнях). Принцип этого метода заключается в разрезании участка фермы и обозначении усилий в этих стержнях. При этом данный разрез не должен будет пересекать более трех стержней.

Усилие в большинстве случаев направляется от узла, что предполагает растянутость стержня. Если в результате усилие получается с отрицательным знаком, это будет свидетельством сжатости стержня.

В чем заключается метод Риттера

Метод Риттера применяется в теоретической механике с целью расчета усилий в стержнях ферм. Его называют также методом моментных точек или сечений. Главным образом, указанный метод применяется с целью расчета плоских ферм.

Метод Риттера представляет точный и простой способ определения усилий в стержнях за счет специального разреза (сечения) фермы. Разрез при этом должен соответствовать определенным условиям:

• поделить ферму на две несвязанные части;
• пересекать максимально три допустимых стержня;
• в каждой из частей необходимо наличие хотя бы одного стержня.

В сторону сечения направляются искомые (неизвестные) реакции разрезанных стержней, что будет соответствовать положительным усилиям растянутых стержней. Сжатость стержня характеризует усилие с отрицательным знаком.

Мысленное разрезание фермы и обозначение усилий предшествуют составлению уравнения равновесия для выбранной части фермы:

$\sum = 0$ (относительно точки Риттера).

Точка Риттера называется также моментальной точкой для сечения стержня. Ее местонахождение отмечено пересечением линий действия усилий в двух остальных стержнях. При этом точка может находиться или на ферме, или непосредственно на продолжении стержней (что далеко за пределами фермы). Если такая точка отсутствует (при параллельности стержней), то уравнение моментов заменяет уравнение проекций на ось, которая перпендикулярна параллельным стержням.

Готовые работы на аналогичную тему

Метод Риттера не считается универсальным. Так, встречаются случаи отсутствия сечения Риттера для конкретного стержня. Главным в данном методе является существование независимого способа для определения усилий таким образом, чтобы исключить влияние значения в одном на значение другого.

Такое влияние, проявленное в накоплении ошибок округления, считается недостатком при использовании метода вырезания узлов. Также бывают и исключения, когда допускается возможность рассечения четырех и более стержней и определения усилия в нужном стержне. При этом составляется только одно уравнение моментов.

Метод Риттера сложно применить при компьютерных расчетах. Более простым в этом отношении считается метод вырезания узлов. При проверке несложных расчетов может быть применен такой графический метод, как диаграмма Максвелла-Кремоны.

Диаграмма Максвелла-Кремоны

Диаграммой Максвелла-Кремоны называется применяемый в теоретической механике графический метод для определения усилий в статически определимых плоских фермах. Его разработчиками были английский физик Дж. Максвелл и итальянский математик Л. Кремона. Применение данного метода также относится к строительной механике и сопротивлению материалов.

Метод основывается на графическом варианте формулировки условия равновесия для системы сходящихся сил – замкнутости многоугольника сил (в т. ч. усилий в стержнях), приложенных к узлу фермы, при равновесии.

Согласно принципу построения многоугольника, начало одного вектора должно приходиться на конец другого. Диаграмма Максвелла-Кремоны формирует правило, исключающее повторное построение усилий.

Построение начинается с определения реакций опор. Для этого применяются аналитические методы, при которых составляются уравнения проекций сил и моментов. Последнее усилие, полученное при построении, будет считаться проверочным, поскольку может быть определено не одним способом.

Считается, что первым вышеуказанный метод предложил в 1864 году именно Максвелл, а Кремона заговорил о нем спустя 8 лет. При этом последний признал приоритет Максвелла. Существуют доказательства того, что сама идея метода впервые была разработана У. Рэнкиным в 1858 году.

В практических расчетах ферм в настоящее время этот метод не применяется как устаревший. На смену ему пришли аналитические (метод вырезания узлов, метод Риттера) и компьютерные методы. Менее известен метод замены стержней Геннеберга (вариант метода сил).

Метод Риттера для расчета фермы

Согласно принципу метода сечений (метода Риттера), ферма будет рассечена на две части. Одна ее часть при этом отбрасывается. Действие фермы отображают усилия, попавшие в сечение, в стержнях той части, которая осталась.

Усилия в стержнях будут направлены к отброшенной части фермы вдоль стержней (предполагается растянутость всех стержней). Исследуемая часть фермы, на которую воздействуют заданные активные силы, усилия в стержнях и опорные реакции, находится в равновесном состоянии. При этом мы наблюдаем формирование произвольной плоской (не сходящейся) системы сил, для которой записываются три уравнения равновесия. Это объясняет ограниченное количество неизвестных (не более трех):

1-я форма записывается так:

При составлении уравнений равновесия предпочтительной будет форма, позволяющая получить простейшие уравнения. Так, если в сечении, например, параллельными будут две неизвестные силы, удобно использовать 2-ю форму уравнений.

Если в сечении все силы попарно пересекаются, то тогда используется 3-я форма уравнений. Точки пересечения сил в таком случае выбираются как моментные точки. Каждое уравнения равновесия, полученное таким образом, будет содержать в себе только одну неизвестную. Сравнительно с методом вырезания узлов, это существенно ускоряет расчет, повышая при этом точность результатов вычислений. Если в сечении неизвестных усилий оказывает более трех, то возникает необходимость в дополнительных сечениях.

Источник

Метод сквозных сечений (метод Риттера)

Метод сквозных сечений – аналити–

ческий метод. Применение этого метода позволяет найти усилие в любом стержне фермы независимо от усилий в остальных стержнях. Для этого нужно суметь составить такое уравнение равновесия, чтобы в нём содержалось, кроме внешних известных сил, только одно усилие в стержне, именно искомое.

Чтобы достичь этой цели, нужно проделать следующие операции:

1) Определить реакции внешних связей для всей фермы.

2) Мысленно рассечь ферму на две части так, чтобы был разрезан исследуемый стержень, и чтобы по обе стороны сечения было не менее двух узлов (иначе операция сведётся к вырезанию узла).

3) Одну часть фермы нужно отбросить, а другую (менее громоздкую) оставить для рассмотрения.

4) Действие отброшенной части фермы заменить реакциями рассеченных стержней, направленными от рассматриваемой части (считаем условно все усилия в стержнях растягивающими).

5) Составить такое уравнение равновесия для рассматриваемой части, чтобы в него входило только одно искомое усилие. Поэтому в большинстве случаев составляются моментные уравнения равновесия. В качестве центров моментов сил выбираются так называемые точки Риттера. Точка Риттера – это точка пересечения осей всех рассечённых данным сечением стержней, кроме одного, исследуемого.

Если рассечены только 3 стержня, то можно составить уравнения равновесия в 3–ей форме записи: ;

; , где точки Риттера E, M, N не лежат на одной прямой. Тогда можно определить усилия во всех

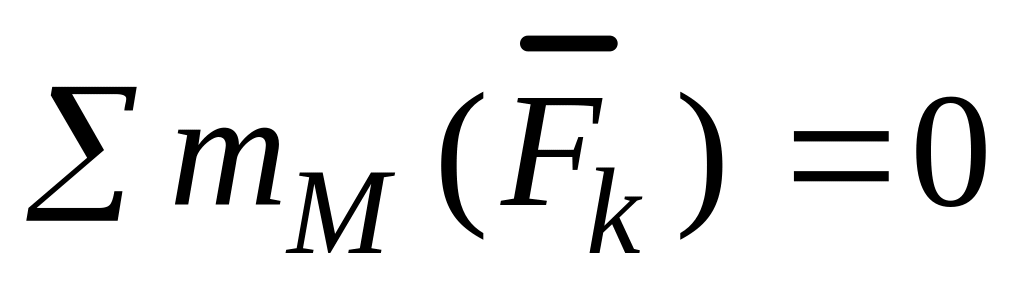
3-х рассечённых стержнях.

В частном случае, когда из 3-х рассечённых стержней два взаимно параллельны, составляются уравнения равновесия во 2-ой форме записи: ; ; , где ось z должна быть перпендикулярна к двум параллельным стержням.

6) Из составленных уравнений определить искомые усилия в исследуемых стержнях.

Замечание: если рассечено более 3-х стержней, то возможны следующие случаи:

а) можно найти только одну точку Риттера и составить только одно уравнение равновесия, соответствующее требованиям метода сквозных сечений;

б) ни одной (такое сечение не годится).

7) Для определения усилий в других стержнях фермы требуется проводить новые сечения и осуществлять перечисленные операции 1–6.

Рассчитать методом сквозных сечений ферму, представленную на рис. 3, с теми же условиями.

1) Реакции внешних усилий найдены ранее: , , .

2) Пусть требуется найти усилия в стержнях 1, 3 и 6. Проводим сечение 1–1,

р 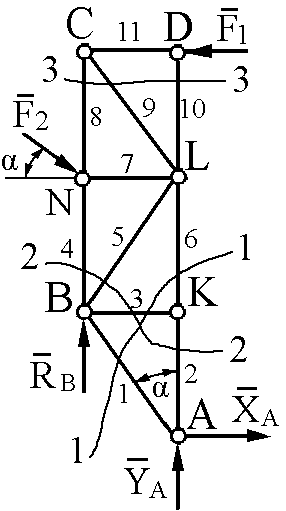ассекающее эти стержни (рис. 7).

3) Отбрасываем мысленно

верхнюю часть фермы, а нижнюю, более простую, вычерчиваем вместе с внешними силами

Для удобства и наглядности заполним

Рис. 7. промежуточные расчёты.

4) Рассеченные стержни 1, 3 и 6 заменим их реакциями , и , направленными от узлов A и K.

5) Так как рассечено только 3 стержня

и все стержни взаимно не параллельны, то можно составить 3 моментных уравнения

равновесия (в 3-ей форме). Точками Риттера будут точки A (пересечение и ), K (пересечение и ), B (пересече–

Если провести сечение 2–2, т.е. рассечь 4 стержня (2, 3, 4 и 5), то можно обнаружить только одну точку Риттера – B (пересечение стержней 3, 4 и 5). Значит можно составить только одно уравнение равновесия и найти одно усилие (см. замечание к п. 6 и таблицу 3).

Для определения усилий , и проведём сечение 3–3 (см. рис. 7), пересекающее три стержня 8, 9 и 10. Заметим, что стержни 8 и 10 взаимно параллельны. Учитывая рекомендации п.5, составляем 3 уравнения равновесия во 2-ой форме (см. табл. 3).

Чтобы найти усилие , можно рассечь стержни 4, 7, 9 и 11. Единственной точкой Риттера будет точка C пересечения всех рассечённых стержней, кроме стержня 7.

Источник

Определение усилий в стержнях по способу Риттера. (Момент силы относительно точки). 11636

Используем метод сечений для нахождения усилий в стержнях плоских ферм. Рассмотрим ферму, изображённую на рис. 3.8. На ферму действуют вертикальные внешние силы: реакции опор R_A = 40 кН и R_B = 20 кН и нагрузка F = 60 кН.

Рис. 3.8. Схема фермы

При определении усилий все стержни фермы условимся считать растянутыми, знак «минус» в ответе будет означать, что стержень сжат. Допустим, требуется определить усилие в стержне 6 фермы. Для этого проводим сечение I-I, рассекая не более трех стержней, в том числе стержень 6, усилие в котором определяется. Мысленно отбрасываем левую часть фермы, заменяя ее действие на оставшуюся правую часть усилиями N₆, N₇ и N₈, приложенными в соответствующих сечениях стержней и направленными в сторону отброшенной части (рис. 3.9).

Рис. 3.9. Оставшаяся часть фермы

Чтобы определить усилие N₆ независимо от усилий N₇ и N₈, составляем уравнение моментов сил, действующих на правую часть фермы, относительно точки К, в которой пересекаются линии действия сил N₇ и N₈. Эту точку называют точкой Риттера:

кН.

Воспользуемся тем же сечением для определения усилия N₇, независимо от усилий N₆ и N₈. Спроецируем все силы, действующие на правую часть фермы, на вертикальную ось Y, так как проекции сил N₆ и N₈ на эту ось равны нулю:

кН.

Для определения усилия N₈ составим уравнение моментов этих же сил относительно точки Риттера L, в которой пересекаются линии действия сил N₆ и N₇:

кН.

Знаки полученных ответов показывают, что стержень 6 растянут, а стержни 7 и 8 сжаты.

Такой способ определения усилий в стержнях фермы предложен Риттером и носит название способа Риттера.

Вопросы для самопроверки

1. Что такое момент силы относительно точки?

2. Будет ли изменяться момент силы относительно точки, если, не меняя направления, переносить силу вдоль линии ее действия?

3. На тело действуют две силы F₁ = 40 Н и F₂ = 50 Н, как показано на рис. 3.10 (а = 0,5 м, b = 0,8 м, a = 30°). Какая из сил создает больший момент относительно точки О?

Рис. 3.10. К вопросу 3

4. Что такое главный вектор и главный момент плоской системы сил?

5. Как аналитически найти главный вектор и главный момент данной плоской системы сил?

6. В чем сходство и в чем различие между главным вектором плоской системы сил и ее равнодействующей?

7. Сформулируйте теорему Вариньона.

8. Какие уравнения (и сколько) можно составить для уравновешенной произвольной плоской системы сил?

9. Перечислите различные виды нагрузок на балку.

10. Какие виды опор балок вы знаете?

11. Сформулируйте основной закон трения. Что такое коэффициент трения, угол трения и от чего зависит их значение?

12. Брус находится в равновесии, опираясь на гладкую вертикальную стену и шероховатый горизонтальный пол; центр тяжести бруса находится в его середине. Можно ли определить направление полной реакции пола?

Источник