- Формирование умений обобщённым способом решать математические задачи у младших школьников. статья (математика) по теме
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- Обобщенный способ рассуждения при решении математической задачи как вариант постановки и решения учебной задачи
- Библиографическое описание:
- Дипломная работа: Обобщения при обучении решению математических задач
Формирование умений обобщённым способом решать математические задачи у младших школьников.
статья (математика) по теме
Решение задач у большинства младших школьников вызывает трудности. Одна из причин — образ мышления у детей абстрактный. Другая — многие дети плохо читают и не понимают содержания задачи. Статья знакомит с этапами формирования умений решать задачи; способами подготовки учащихся к решению простых и составных задач; разнообразными видами работ над решённой задачей; способами составления задач учащимися; способами проверки решения задач.
Скачать:
| Вложение | Размер |
|---|---|
| formirovanie_umeniy_obobshchyonnym_sposobom_reshat_matematicheskie_zadachi_u_mladshih_shkolnikov.doc | 62.5 КБ |
Предварительный просмотр:
Формирование умений обобщённым способом решать математические задачи у младших школьников.
Решение задач у большинства учащихся вызывает трудности. Это происходит потому, что дети в начальной школе думают образно, а мы хотим, чтобы они сразу думали абстрактно. Другая причина в том, что многие учащиеся не умеют читать, поэтому не понимают содержание задачи и не могут её решить.
Формирование умений решать задачи можно представить в виде лесенки:
Составление “своих” задач
Составление обратных задач
Самостоятельное решение составных задач
Опыт решения составных задач
Знакомство с составными задачами
Решение простых задач
Понятие о задаче
Итак , на первом этапе учащихся надо познакомить с понятием “задача”.
Далее дети должны ответить на вопрос «Задача это или не задача?». Потом довести до сознания детей, что для ответа на вопрос задачи необходимо, чтобы было не менее двух числовых данных. Это можно достигнуть путём решения простых задач без числовых данных, с неполными данными.
Ключ к решению задачи – это её анализ , на основе которого устанавливается зависимость между данными и искомыми значениями.
В методике анализа задачи используют два разбора: аналитический (от вопроса к числовым данным) и синтетический (от числовых данных). Эти способы являются средством раскрытия пути решения задачи.
Подготовка учащихся к решению составных задач начинается уже в процессе решения простых задач. Вот несколько из них:
поставить вопрос к данному условию;
какие ещё вопросы можно поставить;
какие вопросы можно поставит, чтобы задача решалась так:
дополнить условие задачи (если нет данных);
решение задач с двумя вопросами;
решение двух простых задач, связанных между собой так, что вторая является продолжением первой.
Работа над задачей делится на этапы:
представление модели содержания задачи;
составление плана решения, запись решения;
Кроме того, целесообразно использовать разнообразные виды работ над решённой задачей. Такие как:
другая форма записи (выражением);
другой способ записи (уравнением);
решение задачи другим (арифметическим способом);
исследование готового решения (ставим вопросы: если бы был другой вопрос, может ли быть…, сколько способов решения задачи);
преобразование задачи (изменение числовых данных, изменение вопроса, добавление вопросов, чтобы добавилось действие);
сопоставление рисунков, схем с данной задачей;
нахождение ошибок в моделировании;
нахождение ошибок в решении.
Высшая ступень в работе над задачей – это составление задач учащимися:
— по заданному сюжету;
по предметной картинке;
по картинке и выражению;
по схеме (на основе заданной модели);
по аналогии: по сюжету, по числовым данным, по способу решения;
с буквенными данными.
При обучении математике необходимо формирование самоконтроля у учащихся, т.е. умения оценить себя, свою работу, сделать проверку.
Способы проверки решения задач разнообразны:
прикидка – установление, какое число в результате получится;
самоконтроль по алгоритму решения;
использование графической иллюстрации;
установление соответствия между числами, полученными в результате и данным в задаче;
проверка решения уравнением;
способы, основанные на моделировании (они позволяют проверить не только результат, но и правильность выбора действия).
По теме: методические разработки, презентации и конспекты
РЕКОМЕНДАЦИИ ДЛЯ ПЕДАГОГОВ И РОДИТЕЛЕЙ ЗАСТЕНЧИВЫХ ПЕРВОКЛАССНИКОВ.
Источник
Обобщенный способ рассуждения при решении математической задачи как вариант постановки и решения учебной задачи
Дата публикации: 16.03.2016 2016-03-16
Статья просмотрена: 450 раз
Библиографическое описание:
Сизова, М. Н. Обобщенный способ рассуждения при решении математической задачи как вариант постановки и решения учебной задачи / М. Н. Сизова. — Текст : непосредственный // Молодой ученый. — 2016. — № 5.6 (109.6). — С. 88-90. — URL: https://moluch.ru/archive/109/27015/ (дата обращения: 19.11.2021).
В статье представлена технология обучения младших школьников обобщенному способу решения задач с позиций величинного подхода, демонстрируется возможность формирования обобщения как универсального учебного действия в обучении решению составных текстовых задач.
Ключевые слова: обобщенный способ деятельности, формирование обобщений, обучение решению задач.
Одним из принципов развивающего обучения является принцип изначального максимально возможного широкого обобщения (А.К. Артемов). О таком подходе в обучении математике Алексей Кириллович Артемов писал еще в восьмидесятые годы прошлого века. Учащиеся изначально усваивают обобщенный способ деятельности, охватывающий все случаи в пределах данной совокупности. Это позволяет построить обучение по третьему типу учения школьников, который является наиболее эффективным в обучении (Н.Ф.Талызина и др.). В настоящее время развитие ученика стало стратегической целью образования. Учащиеся при этом включаются в процесс решения учебных задач, результатом решения которых является уяснение ученикомобщего способа решениявсех задач из данной совокупности. В результате решения учебной задачи у учащегося появляется обобщенное знание, выполняющее функцию метода в учебном познании и обучении, которое учащийся может использовать самостоятельно для решения конкретной задачи из такой совокупности. Это —его вновь приобретенное интеллектуальное умение.
В школьной практике не обозначенная, не выделенная учебная задача или нечетко понятая может порождать методические ошибки и неточности. А.К.Артемов выделяет следующие типичные случаи:
- В вопросах учителя детям нет четкой направленности на необходимое обобщение, составляющее результат решения учебной задачи. Нередко это наблюдается при частично открытой форме задания последней.
- В действиях учителя непреднамеренно происходит подмена одного обобщения другими, т. е. подмена в ориентации от решения одной учебной задачи на другую, в результате чего снижается эффект обучения.
- Своими действиями учитель не ориентирует учащихся на решение какой-либо учебной задачи, т. е. не подводит их к обобщениям.
Особенно отчетливо это становится заметно при организации процесса усвоения решения составных текстовых математических задач.
Рассмотрим один из способов формирования обобщения на примере решения текстовой задачи.
Выделяют два типа задач (С.П.Зубова). К первому относятся такие задачи, в которых все величины измеряются только по одной шкале (выбирается одна мерка для измерения). Второй тип задач – это задачи, в которых даются результаты измерения величин по разным шкалам (выбираются разные мерки для измерения одной и той же величины). В каждом из типов также можно выделить разные виды задач.
Рассмотрим второй тип задач.
Это могут быть задачи, где рассматривается некоторая величина, измеренная при помощи двух мерок. Условно назовем их «мерка первого рода» и «мерка второго рода». Также в задаче речь идет о кратном отношении мерок (или соответствии): количество мерок (часть мерки) первого рода относится к единице второго рода, количество мерок (часть мерки) второго рода относится к единице первого рода. Обычно, в задаче одна из трех характеристик величины (мерка первого рода, мерка второго рода, их кратное отношение) неизвестна и ее требуется найти. Учитывая, рассмотренное разнообразие всех характеристик, только варьируя данные показатели можно выделить 6 видов задач.
Анализ данных задач целесообразно начинать с поиска мерок каждого рода и кратного отношения. Составляется таблица. Запись традиционно выглядит следующим образом. В первом столбце записываем отношение количества мерок первого рода к единице (мерке) второго рода, во втором столбце — количество мерок второг рода, в третьем столбце – количество мерок первого рода. Таким образом можно обозначить обобщенно то умение, которое необходимо сформировать у учеников. Задача учителя состоит в том, чтобы найти формулировки и пути (часто это система вопросов) для прояснения обобщенного способа поиска величин, их записи в таблице или обозначения на схеме.
Например, дана задача.
За 1 час пешеход проходит 5 км. Сколько километров он пройдет за 4 часа?
Сначала могут быть поставлены следующие вопросы:
— О каком процессе идет речь в задаче?
(Возможный ответ) Речь идет о движении или преодолении пути.
— Путь измеряется в задаче в каких мерках?
(В.О.) Путь или расстояние мы измеряем в километрах.
— Что можно сказать о процессе преодоления пути? Есть ли что-то в условии, что помогает нам уточнить, как пешеход преодолевает весь путь? А часть пути?
— Как преодолевает пешеход часть пути?
(В.О.) Пешеход преодолевает часть пути за 1 час.
— Какую часть пути (расстояния) пешеход преодолевает за 1 час?
— Что же известно нам о части пути и его преодолении?
(В.О.) Что часть путь в 5 км можно преодолеть за 1 час.
Так как путь в задаче «измеряется при помощи двух мерок»: в километрах и в часах, требующихся на его преодоление, то речь идет о расстоянии и времени. Так как в задаче есть кратное отношение (5 км за 1 час), то мерка первого рода — это километр, соответственно величина первого рода – расстояние. Мерка второго рода – часы, величина – время. Таким образом, поиск столбцов таблицы и их наименований завершен.
Расстояние за 1 час
Для решения задачи используются обобщенные правила. Для того чтобы найти значение величины первого рода необходимо значение кратного отношения умножить на значение величины второго рода. Для того чтобы найти значение величины второго рода необходимо значение величины первого рода разделить на значение кратного отношения. Для того чтобы найти значение кратного отношения необходимо значение величины первого рода разделить на значение величины второго рода.
В предложенной задаче необходимо найти значение величины первого рода, поэтому, используя правило, получим 5 4 = 20 (км).
Можно предложить для сравнения учащимся следующую задачу.
На то чтобы пройти 1 км пешеходу потребуется 12 минут. Сколько километров он пройдет за 4 часа.
Речь в данной задаче также идет о пути и его преодолении, измеряется этот процесс при помощи двух мерок, и соответственно характеризуется двумя величинами – временем и расстоянием. В задаче есть кратное отношение (12 минут на 1 км), следовательно, мерка первого рода — это минуты, а величина – время, мерка второго рода – метры, величина – расстояние. Необходимо найти величину второго рода, значит, 240 : 12 = 20 км
При подобных рассуждениях становится несущественным является ли рассматриваемая в задаче величина скоростью или это – величина обратная скорости. В обоих случаях мы рассуждаем одинаково.
Такого рода обобщение может показаться избыточным. Однако, именно данный подход к рассмотрению подобных задач, способствует формированию наиболее обобщенного представления о зависимостях между величинами и результатом решения является уяснение ученикомобщего способа решениявсех задач из данной совокупности.
Чаще рассуждение строится таким образом, что при введении величин — скорость, цена, расход в 1 день и т.п. – обращается внимание, что все они «укладываются» (помещаются плотно, идеально) в подобную «величину» — расстояние, стоимость, всего израсходованного и т.п. При этом обобщение не охватывает ситуации с введением величин обратных скорости, цене и т.п.
При рассуждении об укладывании может возникнуть соблазн подмены обобщения. Может проговариваться или уясняться из подобранных заданий тот общий внешний признак, что величина, которая «укладывается» меньше той, на которую «укладывают».
Ясно, что обобщение относительно, тот или иной факт может быть обобщением для второго факта или конкретизацией для третьего. Выбор уровня обобщения и соответствующей формулировки остается за учителем и учениками, в смысле принятия задачи. Важно не допускать ошибок, которые были обозначены выше, иначе это может привести к неверно или неполно сформированной ориентировочной основе действия, что приведет к появлению ошибок и, в конечном счете, проявиться в неумении решать задачи.
- Артемов, А. К., Тихонова Н. Б. Основы методического мастерства учителя в обучении математике младших школьников: пособие для учителей и студентов факультета педагогики и методики начального образования. / А.К. Артемов, Н.Б. Тихонова – Самара, 1999. — 93 с.
- Зубова, С.П. Обучение решению задач в начальных классах: Учебно-методическое пособие для студентов факультета начального образования. / С.П.Зубова – Самара: ООО «Офорт», Самарский государственный педагогический университет, 2003. – 96 с.
- Талызина, Н.Ф. Формирование познавательной деятельности младших школьников. / Н.Ф.Талызина — М.: Просвещение, 1988. — 175 с.
Источник
Дипломная работа: Обобщения при обучении решению математических задач
| Название: Обобщения при обучении решению математических задач Раздел: Рефераты по педагогике Тип: дипломная работа Добавлен 07:56:42 09 ноября 2010 Похожие работы Просмотров: 487 Комментариев: 20 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Решение конкретной задачи | Решение обобщенной задачи |
| Найти число, 2% которого равны 12 | Найти число, если известен процент и его значение. |
| 1. Найдем сколько составляет один процент от числа. для этого: 12:2=6 | 1. Нахождение числа, которое приходится на один процент заданного числа. |
| 2.так как все число составляет 100%, умножаем число, полученное на один процент на 100: 6*100=600 | 2. Умножение полученного числа на 100. |
| Итак, число равно 600 | 6. Запись ответа |
Решение рассмотренной конкретной задачи приводит и к такому обобщению: для того, чтобы найти число, если известно, сколько составляет конкретное число процентов от него, нужно найти, сколько составляет один процент заданного числа, а зачем умножить это значение на 100.
Специализация метода решения задач на отыскание числа, если известен процент и его значение позволяет решать все задачи этого класса.
Пример 7. Фабрика выпускает калькуляторы партиями. Брак в каждой партии обычно бывает 9 калькуляторов, что составляет 2% от общего количества. Сколько калькуляторов в одной партии?
Так же обобщение может осуществляться путем абстрагирования от конкретных сюжетов нескольких задач и построения общей математической модели для различных по фабуле задач.Математическая модель задачи производится переводом реально происходящих в действительности процессов и явлений на язык математики и позволяет показать применение математики как инструмента для математизации реальных практических ситуаций. Таким образом, моделирование является обобщением нескольких задач и методом решения различных классов задач.
Пример 8. Клоун на ходулях хочет показать мастер – класс и обойти всю арену по краям за 5 шагов и вернуться в исходное место, при этом для красоты шаги должны быть одинаковы. Помогите клоуну, указав ему путь по арене.
Пример 9. 5 спасателей натягивают батут круглой формы для спасения человека. Как лучше спасателям держать батут, чтобы натяжение было наилучшим.
Сравнение и анализ геометрических моделей этих задач приводят к выводу: задачи, несмотря на различие формулировок, имеют одинаковые геометрические модели.
Абстрагируясь от конкретных фабул задач, формулируют обобщенную задачу: в окружность вписать правильный пятиугольник.
Понять, что для решения задачи необходимо только вписать правильный пятиугольник в окружность, мы смогли тогда, когда построили геометрическую модель задачи. Решение обобщенной задачи позволяет так же решать все задачи такого типа.
Обобщение применимо при переходе от конкретных задач к общим моделям их решения, а затем к методу решения класса аналогичных задач.
Пример 10: изучение пропорциональных зависимостей величин в 7 классе: скорость, время, расстояние (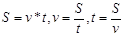
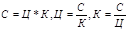
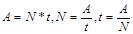
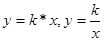
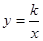
Так же распространено обобщение решения различных конкретных задач до метода решения класса задач.
Пример 11. Введение метода построения вспомогательных треугольников, который позволяет на протяжении изучения всего курса геометрии решать многие задачи на построение единым подходом, хотя они могут быть и различного содержания.
Суть метода – построение вспомогательных треугольников и использование их свойств и вновь полученных элементов для окончательного решения задачи [18].
Данные удобно представить в виде таблицы. [Приложение 8]
На анализе построение трех задач можно вывести общий метод построения всех задач такого класса, который записывается в последний столбец таблицы. При таком подходе учащиеся четко различают этапы метода.
2.1.2 Обобщение методов решения задач
При изучении методов решения математических задач индуктивные обобщения могут осуществляться следующим образом:
1) обобщение и систематизация способов решения конкретных задач до методов решения класса задач;
2) обобщение и систематизация методов решения класса задач.
Для систематизации знаний учащихся, приобретенных при решении конкретных задач, полезно делать обобщения решений до метода решения класса задач.
Пример 12: обобщение и систематизация методов решения задач о длине окружности и площади круга.
После решения ряда задач с применением формул длины окружности и площади круга в 9 классе на уроке геометрии можно провести с учащимися обобщающую беседу.
Основными при изучении темы «длина окружности и площадь круга» являются шесть объектов: R– радиус, С – длина окружности, S – площадь круга, угол с градусной мерой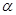
В беседе следует отметить, что формула длины дуги это обобщенный случай формулы длины окружности, то есть когда угол равен 360 0 . Аналогичное обобщение можно провести и с формулой площади круга до формулы площади сектора. Тогда количество объектов уменьшится с шести до четырех и можно рассмотреть два основных соотношения между ними:
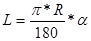
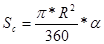
Если заданы два компонента из четырех, то две оставшиеся могут быть вычислены. Таким образом, возможные типы задач определяются данными: 1) L,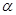
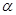
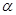
Если же речь идет о длине окружности и площади круга, то количество типов задач уменьшается. Целесообразно провести специализацию и рассмотреть этот случай. Обобщение показывает взаимосвязь нахождения длины окружности и длины дуги окружности, площади круга и площади сектора, так как такие громоздкие формулы плохо запоминаются учащимися.
Такие обобщения позволяют выявить связи изучаемого с изученным ранее и сформировать как общие методы решения классов задач, так и систему методов решения задач.
Индуктивные обобщения методов решений задач, а так же их систематизация приводят к формированию системы советов решающему математическую задачу.
2.1.3 Обобщение способов поиска решения многих задач до системы советов
В процессе решения задачи деятельность учащегося направлена на понимание задачи, осуществление поиска ее решения. Таким образом, она направлена на осознание, систематизацию и выяснение той информации, которая является явной в задаче.
Советы при решении различных задач должны обладать общностью, должны быть естественны и просты.
Все советы можно разделить на четыре группы, которые соответствуют четырем этапам решения задачи: усвоение содержания задачи; составление плана решения задачи; реализация плана решения задачи; анализ и проверка правильности решения [30]. На первом этапе деятельности целью является достижения осознанного понимания словесной формулировки задачи. Взгляд на один и тот же факт или объект задачи с различных сторон помогает оценить связь объекта задачи с другими данными или внешней информацией. На втором этапе должны быть установлены связи различных объектов в задаче и выявлена связь с внешней информацией, с ранее приобретенным опытом. Учащийся должен внимательно, многократно и с разных сторон рассмотреть все компоненты задачи, их внутренние и внешние связи и осуществить составление плана решения задачи. На третьем этапе осуществляется сам план решения задачи, на четвертом – исследование полученного решения.
Такие этапы помогают направить ход мыслей в нужном направлении для достижения поставленной в задаче цели. Рассмотрим подробно систему советов, например, для составления плана решения задачи.
Это второй этап решения задачи, наступает, когда ученик вник в содержание задачи, ввел все обозначения, по необходимости сделал чертеж.
Для составления верного плана решения задачи необходима подготовка.
А). Для начала следует выяснить, известна ли какая-либо родственная задача? Аналогичная задача?
Пример 12. За одно и то же время велосипедист проехал 4 км, а мотоциклист – 10 км. Скорость мотоциклиста на 18 км/ч больше скорости велосипедиста. Найдите скорость велосипедиста.
Пример 13. Лодка за одно и то же время может проплыть 36 км по течению реки или 20 км против течения. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч [17].
Задачи аналогичны по плану решения. В обеих для решения необходимо составить отношения расстояний к скоростям и приравнять. Общая формула выглядит следующим образом: 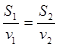
Б). Подумать, известна ли задача, к которой можно свести решаемую?
Пример 14 . Отрезки, концами которых служат внутренние точки противоположных сторон квадрата, перпендикулярны. Докажите, что эти отрезки равны [38].
Решение задачи упрощается, если заданная пара взаимно перпендикулярных прямых будет проходить через центр квадрата. Доказав равенство отрезков в этом случае, основная задача легко решается использованием признаков параллельности и определения квадрата. Таким образом задачу можно свести к следующей: Отрезки, концами которых служат внутренние точки противоположных сторон квадрата, перпендикулярны и пересекаются в центре квадрата. Докажите, что эти отрезки равны.
В). Если родственная задача неизвестна и свести данную задачу к какой-либо известной задаче не удается, то стоит воспользоваться советом: «Попытайтесь сформулировать задачу иначе». При переформулировании задачи либо пользуются определениями данных в ней математических понятий (заменяют термины их определениями), либо их признаками (точнее сказать, достаточными условиями).
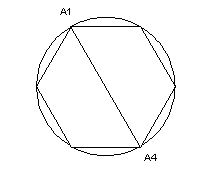
Для быстрого и более легкого нахождения плана
решения данной задачи, удобно к понятию «правильный
|
шестиугольник» добавить определяющий признак, что
«в правильном шестиугольнике».
Тогда задача примет вид: Найти периметр правильного шестиугольника
Тогда, глядя на рисунок 1, становится ясен план решения задачи.
Г). Так же, составляя план решения задачи, следует задать себе вопрос: «все ли данные задачи использованы?» Выявление неучтенных данных задачи облегчает составление плана ее решения. Возможно, имеются «скрытые» данные.
Пример 16. Найти диагональ прямоугольного параллелепипеда, длина а, ширина b , высота h которого известны [30].
Так может случиться, что ученик, зная теорему Пифагора, найдет диагональ грани: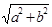
Д). Иногда полезно следовать совету «Попытайтесь преобразовать искомые или данные». При этом данные преобразуют так, чтобы они приблизились к искомым.
Пример 17. Постройте треугольник, равновеликий данному четырехугольнику [38].
При отыскании решения данной задачи следует для начала преобразовать четырехугольник до параллелограмма, так как формулы площадей треугольника и параллелограмма сходны между собой.
Е). Если следуя предыдущим советам, вам не удалось составить план решения, то можно воспользоваться таким советом: «попробуйте решить лишь часть задачи», т.е. попробуйте удовлетворить лишь части условий, с тем, чтобы далее искать способ удовлетворить оставшейся части условий задачи. Этот совет можно расширить, развить до совета: «Расчлените задачу на более простые задачи».

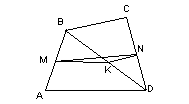
Пример 18. В треугольнике ABC медианы AA 1 , BB 1 , CC 1 пресекаются в точке M . Точки A 2 , B 2 , C 2 являются соответственно серединами отрезков AM , BM , CM . Докажите, что 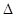
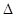
Данная задача решается с применением центральной симметрии,
которая явно не видна (рис. 2). Тогда стоит разбить задачу на этапы:
2) найти центр симметрии; 3) определить центральную симметрию.
Ж) В составлении плана решения задачи может помочь ответ на вопрос: «Для какого частного случая возможно достаточно быстро решить эту задачу?». Отыскав частный случай, можно воспользоваться решением задачи в найденном частном случае для более общего (но, может быть, не самого общего) случая. Так можно поступить, постепенно обобщая задачу до исходной, решаемой задачи. Совет: «Рассмотрите частные случаи задачной ситуации, решите задачу для какого-нибудь частного случая, примените индуктивные рассуждения».
3). Иногда решение задачи оказывается проще, если сформулировать и решить задачу сначала более общую, а затем с ее помощью решить данную задачу. Совет: «Попробуйте сформулировать и решить более общую задачу».
Эвристико-организационные советы для решения задачи можно оформить в виде таблицы. [20] [Приложение 9]
Таким образом, с помощью индуктивных обобщений при решении математических задач можно вывести новые методы решения задач, перейти от одних методов решения задач к более общим. Так же индуктивные обобщения подходов к решению задачи их систематизация помогаютв создании системы советов, полезных в процессе отыскания решения задачи.
2.2 Обобщение как метод решения математических задач
Обобщение как метод решения может осуществляться:
1. Решение задачи «по индукции»;
2. Решение задачи в «общем» виде.
2.2.1 Обобщения «по индукции»
Метод решения задачи «по индукции» основан на полной или теоретической индукции.
Обобщение как метод решения осуществляется по следующей схеме:
1. Выделить частный случай задачи, для которого задача решается легко и решить задачу для этого частного случая;
2. Рассмотреть более общий, но все же частный случай, содержащий первый;
3. Рассмотреть общий случай.
Часто решение задач «по индукции» включает в себя только первый и третий пункты из вышепредложеной схемы.
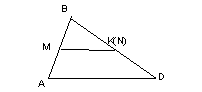
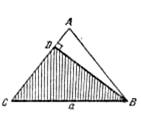
Пример 19. В четырехугольнике две стороны AD и BC не параллельны. Что больше: полусумма этих сторон или отрезок ( MN ), соединяющий середины двух других сторон четырехугольника (рис. 3а)? [3]
|
|
|
1) Выделим для начала частный случай, который можно легко решить. В данном случае будет удобно, если одну из сторон четырехугольника стянуть в точку (рис. 3б). Тогда пусть BC стягивается в точку В. В таком положении точка N совпадает с серединой К отрезка BD, и MN становится средней линией MK треугольника ABD. Таким образом исходная задача сводится к следующей: что больше, половина стороны AD треугольника ABD или отрезок MK, соединяющий середины двух других сторон.
По определению средней линии треугольника ответ очевиден: MK=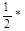
2) Теперь рассмотрим общий случай (Рис. 3в). Задача будет легко решена, если его свести к уже решенному частному случаю. Пусть K – середина диагонали BDчетырехугольника ABCD. Из рассмотренного частного случая имеем: в треугольнике ABDMK=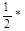
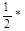

Запишем условия задачи в систему:
Второе уравнение системы выражает делимость искомого числа на 11. Преобразовав систему, получим уравнение: 2*( a + c )=11*( k +1), причем k 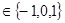
Тогда возможны три случая:
1) k =-1, тогда a + c =0 , тогда a =0 , что противоречит условию (число четырехзначное).
3) k =1 , тогда a + c =11, b =0, d =0 и все значения a и с можно записать в таблицу 2:
| a | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| c | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 |
Число вариантов конечно, снова решив задачу для каждого варианта, находим, что решением задачи будут числа 2090, 3080, 4050, 5060, 6050, 7040, 8030,9020.
Таким образом, чтобы применять обобщение как метод решения задачи «по индукции», нужно уметь выделять частные в случаи задаче.
2.2.2 Решение задач «в общем виде»
Необходимо обучать школьников решению задач «в общем» виде, так как решение задачи «в общем» виде часто может оказаться доступнее, легче, рациональнее, чем решение конкретной задачи. Так же обобщенная формулировка задачи помогает усвоению математической сущности конкретных задач и позволяет обнаружить способ решения исходной задачи. К более общей задаче могут быть применимы методы, которые не применимы к исходной задаче.
Обобщенная задача иногда подсказывает новый способ решения.
Так как модуль раскрывается в зависимости от того, какой знак имеет подмодульное выражение, то обобщением задачи может быть следующая задача: Найти значение выражения F ( a ), если a =0.
Обобщенная задача помогает прояснить суть конкретных задач. При a =0 с положительным.
Иногда задачу удобнее решать сформулировав ее в общем виде.
Пример 24. Даны правильный октаэдр и прямая занимают в пространстве фиксированное положение. Найти плоскость, проходящую через данную прямую и делящую октаэдр на две равновеликие части [30].
Эта задача может показаться сложной, поэтому рациональнее ее сформулировать в общем виде, используя знания о правильном октаэдре: «Даны замкнутая поверхность, обладающая центром симметрии, и прямая занимают в пространстве фиксированное положение. Найти плоскость, проходящую через данную прямую и делящую объем тела, ограниченного данной поверхностью, на две равновеликие части». Искомая плоскость должна проходить через центр симметрии поверхности и определяться этой точкой и данной прямой. Так как октаэдр обладает центром симметрии, тем самым первоначальная задача оказывается найденной.
Так же следует использовать решение задачи в «общем виде» и в задачах с конкретными значениями, но решения которых громоздки. Решение задачи в «общем» виде с последующей подстановкой числовых данных часто позволяет лучше просмотреть план решения задачи, сократить записи, затратить меньше времени на вычисления.
Таким образом, при использовании обобщения как метода решения задач необходимо уметь выделять частные случаи. Так же полезно обучать школьников решению задач в общем виде, так как часто обобщенную задачу решить легче, чем конкретную задачу.
2.3 Обобщение как источник новых математических задач
Обобщения при обучении решению математических задач могут способствовать возникновению новых задач. Новые задачи могут появиться как при исследовании конкретной задачи и ее решения, так и при исследовании обобщенной задачи и ее решения.
К возникновению новой обобщенной задачи могут привести индуктивные обобщения. Обратная операция – специализация, позволяет от обобщенной задачи перейти к конкретным задачам.
Так же с помощью обобщений по аналогии из одной конкретной задачи получают новые конкретные задачи, из обобщенной задачи – новые обобщенные задачи.
Получение новых задач важно тем, что при составлении задач учащиеся усваивают структуру задачи, взаимосвязь данных, данных и искомых, обнаруживают внутреннюю связь между задачами.
Для того чтобы получить новые задачи при помощи обобщений, используют следующие приемы:
1) обобщение данных при сохранении искомых;
2) обобщение (добавление) искомых при сохранении данных;
3) обобщение данных и искомых.
Рассмотрим подробнее эти приемы.
2.3.1 Обобщение данных при сохранении искомых
Замена одних данных (или части данных) другими при сохранении искомых приводит к применению разнообразных приемов и методов решения, казалось бы, близких по содержанию задач. При этом может применяться не один прием, а широкий спектр методов.
Изменением условия задачи при сохранении требования может являться: замена данных более общими; замена одних отношений между объектами задачи другими.
Замена числовых данных задачи параметром часто приводит к обобщенной задаче. Специализация обобщенной задачи помогает получить целый класс аналогичных задач. Конкретные числовые данные можно заменять буквами не все сразу, а последовательно.
Пример 25. «Найти, если сторона нижнего основания равна 10 м, сторона верхнего 5 м и высота пирамиды 6 м» [30].
Если числа 10, 5, 6 заменить буквами, например а, b , h , получим обобщенную задач: «Найти объем усеченной пирамиды с квадратным основанием, если сторона нижнего основания равна a , сторона верхнего b и высота пирамиды h ». Перейдя от задачи «в числах» к задаче «в буквах», мы воспринимаем данные величины как переменные.
Обобщенная задача дает возможность составить и решить еще несколько типов задач, в которых одна из величин является искомой, а остальные – данными.
К появлению новых задачтак жеприводитобобщение понятий, данных в задаче.
Пример 26. Найти диагональ куба, если даны три его измерения (длина, ширина и высота) .
Обобщив понятие куба до понятия прямоугольного параллелепипеда, получим новую задачу:
Пример 27. Найти диагональ прямоугольного параллелепипеда, если даны три его измерения (длина, ширина и высота).
Замена одних отношений между объектами задачи другими тоже может привести к появлению новых задач.
Пример 28. Как изменится частное двух чисел если делимое увеличить в три раза?
Можно исследовать эту задачу и получить новые, размышляя, что произойдет с частным, если делимое увеличить в 3 раза, уменьшить в 3 раза, если изменить делитель, если изменить одновременно делимое и делитель? Возникает целая серия задач, порожденных данной задачей, которые можно записать в таблицу 3.
| Условие задачи | Вопрос задачи |
| Как изменится разность? |
После решения конкретных задач полезно сделать обобщения: если делимое и делитель увеличить или уменьшить в одно и то же положительное число раз, то не изменится; если делимое увеличить, а делитель уменьшить в одно и то же положительное число раз, то частное увеличиться в квадрат этого числа; если делимое уменьшить, а делитель увеличить в одно и то же положительное число раз, то частное уменьшится в квадрат этого числа.
Изменяя отношения между данными задачи, делая их более общими так же можно получить новые задачи.
Пример 29. Доказать, что сумма расстояний, от точки пересечения медиан правильного треугольника до его сторон постоянна .
От этой задачи можно перейти к следующей:
Пример 30. Доказать, что сумма расстояний, от точки взятой произвольно внутри правильного треугольника до его сторон постоянна .
2.3.2 Обобщение (добавление искомых) при сохранении данных
Новая математическая задача может быть получена с помощью изменения требования задачи при сохранении условия: добавления новых заключений; обобщения искомых.
В большинстве случаев в задаче встречается лишь один вопрос, одно заключение, но содержащаяся в задаче информация иногда позволяет сделать и другие выводы (ответить на другие вопросы, сделать другие заключения), т.е. добавить новые заключения при сохранении данных.
Пример 31. Даны две прямые a и b . Доказать, что любая прямая, пересекающая прямую a , пересекает и прямую b , то прямые a и b параллельны. [1]
Вначале требуется доказать параллельность прямых a и b . Тогда прямая, пересекающая a будет не только пересекать прямую b , но и обладать свойствами над этими прямыми: их накрест лежащие, соответственные и углы будут равны, а сумма односторонних будет равна 180 0 . Поэтому можно сформулировать более общую задачу.
Пример 32. Даны две прямые a и b . Доказать, что любая прямая, пересекающая прямую a , пересекает и прямую b , то прямые a и b параллельны, их накрест лежащие, соответственные и углы будут равны, а сумма односторонних будет равна 180 0 .
Задачи, которые приучают учащихся рассматривать всевозможные заключения из данных посылок, что бывает необходимо при решении многих задач на доказательство, при доказательстве различных теорем, иногда называют задачами «без вопросов».На основе решения таких задач удобно рассматривать обобщения о искомых в задаче.
Пример 33. Дана прямоугольная призма, в основании которой трапеция. Установите всевозможные взаиморасположения прямых, содержащих ребра данной призмы.

находиться в трех положениях: быть параллельны,
пересекаться, быть скрещивающимися. Учащиеся, находя
|
параллельные, скрещивающиеся и пересекающиеся прямые, делают выводы о свойствах призмы: что для каждой прямой, находящейся в плоскости одного основания всегда есть прямая, параллельная в плоскости другого основания; все прямые, содержащие боковые ребра параллельны; каждая прямая, содержащая боковое ребро, пересекается с двумя прямыми, содержащими ребра оснований, с остальными скрещивается.
2.3.3 Обобщение данных и искомых
Нередко обобщение данных задачи приводит к обобщению искомых.
Так, обобщение понятий, в условии задачи может привести к обобщению вопроса задачи. Таким образом, теорема косинусов является обобщением теоремы Пифагора.
Пример 34. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Пример 35. В произвольном треугольнике квадрат стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Обобщение данных и искомых задачи до параметра так же приводит к составлению новых задач. Например, зная, что правильный треугольник определяется любым элементом, можно составить задачи, связывающие между собой элементы правильного треугольника: стороны, медианы, радиусы вписанной и описанной окружностей.
Таким образом, мы показали как обобщения при обучении решению математических задач приводят в возникновению новых задач. Это происходит в результате исследования задач и их решений, а так же исследований обобщенных задач и их решений. Используя обобщение и специализацию, учащиеся могут сами составлять новые задачи, осуществляя замену части данных другими при сохранении искомых, добавляя новые заключения или обобщая искомые.
2.4 Обобщения задач ведущие к формированию понятий и теорем
С помощью обобщений можно осуществлять введение понятий и теорем. При этом происходит мотивация введения понятий и теорем, учащиеся сами осознают, как получили и для чего нужно новое знание, определяют его место в системе других понятий или теорем, и легко применяют его при решении различных задач.
При формировании понятий различают обобщения: 1) от конкретных примеров до математического понятия; 2) самих математических понятий.
К определению понятия часто приводит обобщение конкретных примеров.
Пример 36. Определение средней линии треугольника, в основном, в учебниках геометрии вводится дедуктивно. При этом большинство учащихся плохо усваивают определение средней линии треугольника или путают его с теоремой о средней линии треугольника.
Данное определение можно ввести, выделив отличительное свойство средней линии треугольника: соединение середин двух сторон треугольника.
Формирование понятия происходит в три этапа:
1) Выделение общего свойства у класса примеров. Глядя на рисунок 6, уместно задать вопрос ученикам: какими общими свойствами обладает линия
При таком обобщении учащиеся анализируют рисунки, находят в них общее свойство, которое сохраняется во всех данных рисунках: MNсоединяет середины двух сторон треугольника. Это свойство включается в определение средней линии треугольника: средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
2) Осуществление специализации на следующем примере (рис. 7).
Необходимо найти средние линии.
|
Так же вместе с примерами объектов, удовлетворяющих
определению понятия необходимо привести контрпримеры, объекты, которые к изучаемому понятию не относятся (рис. 8).
|
Таким образом сформированное понятие четко осознается учащимися, а выделенное свойство и приведенные контрпримеры помогут быстро отличать его от других.
При обобщение планиметрии до стереометрии происходит большинство переходов от одних понятий к другим, более общим.
Пример 37. Обобщение параллельности прямых на плоскости до параллельности прямых в пространстве может осуществляться так: вспомнить определение параллельности прямых на плоскости: «Две прямые на плоскости называются параллельными, если они не пересекаются» ; рассмотреть две прямые в пространстве. В результате беседы приходим к выводу, что для определения параллельности двух прямых в пространстве, необходимо, чтобы они принадлежали одной плоскости; обобщить определение параллельности прямых на плоскости до определения параллельности прямых в пространстве: «Две прямые в пространстве называются параллельными, если они принадлежат одной плоскости и не пересекаются ».
По такому же принципу происходит обобщение квадрата до куба, площади параллелограмма до объема параллелепипеда, и другие.
Индуктивные обобщения при изучении теорем так же необходимы.
В основе любой теоремы лежит задача на доказательство. Поэтому осуществление обобщений при решении задач на доказательство позволяют учащимся увидеть возникновение теоремы, метода её доказательства, установить связь между различными теоремами, сформулировать новые, систематизировать теоремы и методы доказательства. Это облегчает проведение мотивации при введении теорем, приводит к осознанному восприятию идей доказательства, к пониманию и усвоению содержания теоремы, разумному применению теоремы для решения задач.
Индуктивные обобщения при решении задач на доказательство можно разделить на:
1) обобщение конкретных задач до формулировки теоремы;
2) обобщение теорем.
Индуктивное обобщение конкретных задач до теоремы состоит в том, что в результате сравнения и анализа решения нескольких конкретных задач можно выдвинуть гипотезу для общего случая и вывода теоремы.
Пример 38. Доказать, что если в четырехугольнике сумма противоположных углов равна 180 0 , то около этого четырехугольника можно описать окружность.
Задачу можно обобщить до формулировки теоремы:
«В любом вписанном четырехугольнике сумма противоположных углов равна 180 0 ».
Возможно обобщение самих теорем до более общих. Любая доказанная теорема становится началом для открытия новых фактов и соотношений, доказательств новых теорем, т.е. входит в их доказательства.
Например, теорема о параллельности прямой и плоскости в пространстве обобщается до теоремы о параллельности трех прямых в пространстве, которая может быть обобщена до признака параллельности двух плоскостей.
При таких обобщениях расширяется множество объектов, к которым применимы рассматриваемые свойства и часто сохраняются методы доказательства.
Так же сами теоремы являются обобщениями ранее известных. Для соединения знаний в систему необходимо проводить обобщения теорем и показывать переходы от одних теорем к другим.
Так, обобщая теорему «площадь прямоугольного треугольника равна половине произведения катетов », отбросим ограничение, что треугольник прямоугольный и получим теорему «Площадь произвольного треугольника равна половине произведения двух сторон на синус угла между ними ».
От теоремы «Середины сторон выпуклого четырехугольника являются вершинами параллелограмма» можно перейти к теореме «Точки, делящие стороны четырехугольника в одном и том же отношении (соединенные определенным образом) являются вершинами параллелограмма», а можно перейти к теореме стереометрии: «Середины сторон пространственного четырехугольника являются вершинами параллелограмма».
Таким образом, обобщение при формировании понятий и введении теорем очень полезно. Обобщение знания от конкретных задач до понятия и от задач на доказательство к доказательству теорем помогает проведению мотивации введения понятий и теорем, применению их при решении различных задач.
2.5 Таблицы как средство обобщения при обучении решению математических задач
При обучении решению математических задач удобно проводить обобщения, когда информация представлена в таблицах. Такие таблицы будем называть обобщающими.
Обобщающие таблицы служат для проведения сравнения и анализа математических задач и их решений, при систематизации способов и методов решения задач, при составлении системы советов для поиска решения задач, при выводе понятий и обобщении материала, используемого при решении задач.
При выводе метода решения задач удобно решение по этапам записывать в таблицу. При этом таблица будет состоять из двух столбцов: в первом – решение конкретной задачи, во втором – общий метод решения или алгоритм метода решения задач такого класса.
Для более глубокого понимания метода решения задачи очень эффективно дополнение таблицы еще одним столбцом, в котором показана специализация метода на еще одной конкретной задаче.
Пример 39. Общий алгоритм применения метода координат к решению математических задач можно вывести, проведя анализ решения задачи, к которой применим этот метод. Метод заключается во введении прямоугольной системы координат и записи условия задачи в координатах, после чего решение задачи легко провести с помощью алгебраических вычислений. Необходимо пошагово расписать решение задачи в первом столбце и записать обобщенный алгоритм решения во втором столбце [Приложение 10].
Так решение конкретной задачи приводит к выводу общего алгоритма решения класса задач методом координат:
1. Изучить условие задачи, ввести прямоугольную систему координат так, чтобы одна из точек фигуры являлась центром, и хотя бы одна сторона лежала на какой-либо оси.
2. Обозначить координаты точек во введенной системе координат
3. Используя нужную формулу, составить равенство, которое необходимо доказать, и доказать его в координатной форме.
4. Записать ответ.
Использование метода координат позволит решать и другие задачи.
После вывода алгоритма полезно сразу провести его специализацию на второй задаче, оформив все записи в таблицу.
Так же обобщающие таблицы удобно использовать при выводе нового понятия. При этом понятие формулируется на основе решенных задач, подводящих к его определению.
Пример 40. К определению понятия ромба можно подвести, решив три задачи определяющие его характеристические свойства и сделав вывод.
В учебнике [1] дается такое определение ромба: «Ромбом называется параллелограмм, у которого все стороны равны ». Далее приводится особое свойство ромба: «Диагонали ромба взаимно перпендикулярны и делят его углы пополам ». Для целостного осознания понятия «ромб» следует определение ввести вместе со свойством.
И так, требуется три задачи:
1) задача, подводящая к определению понятия: ромбом называется параллелограмм, у которого все стороны равны;
2) задача, подводящая к первой составляющей свойства ромба: диагонали взаимно перпендикулярны;
3) задача, подводящая ко второй составляющей свойства ромба: диагонали делят его углы пополам.
Все данные удобно оформить в таблицу [Приложение 11].
Решив все три задачи, следует приступить к заполнению четвертого столбца.
Из первой задачи следует определение ромба. Из условия второй задачи следует, что параллелограмм ABCD – ромб, и в нем диагонали пересекаются под прямым углом. Результатом решения третьей задачи является выяснение, что параллелограмм ABCD – ромб и к любому ромбу будет применимо условие задачи, что его диагонали делят углы пополам.
В результате такого способа формирования, понятие «ромб» гораздо лучше усваивается учащимися, чем введение понятия дедуктивно.
Широкое применение таблиц отмечается при обобщении материала, используемого при решении задач. Такие обобщающие таблицы могут быть использованы для различных целей: повторить и систематизировать знания, установить причинно-следственные связи между свойствами объектов, изложить материал укрупненными блоками, рационально заучить и воспроизвести материал [15].
Особое место среди обобщающих таблиц занимают динамические обобщающие таблицы. Они четко отражают взаимосвязи объектов в таблице и логику обобщения.
Примерами таких таблиц могут быть: обобщающая таблица свойств действительных чисел ивекторов в школьном курсе математики [15] [Приложение 1] и сравнительнаятаблица связи векторов в геометрии и физике [15] [Приложение 2]. Примером обобщающей таблицы систематизации знаний учащихся может служить динамическая обобщающая таблица основных тригонометрических формул и их взаимосвязей [10] [Приложение 3].
Таким образом, для лучшего понимания процесса сравнения и анализа задач, при систематизации методов решения задач, при выводе понятий и обобщении материала, используемого при решении задач, удобно использовать обобщающие таблицы.
2.6 Опытное преподавание
Цель: апробация методических рекомендаций на уроках математики в 10-м классе, выявление их влияния на результативность обучения школьников решению задач.
Место проведения : муниципальное общеобразовательное учреждение гимназия №2 города Кирово – Чепецка Кировской области.
Время проведения : 2007–2008 учебный год.
Учитель : Останина Ольга Александровна, учитель математики высшей квалификационной категории.
Содержание опытного преподавания .
Учитель систематически и целенаправленно в соответствии с методическими рекомендациями осуществлял обобщения решения задач при изучении различных тем алгебры и начала анализа и геометрии.
Приведем некоторые примеры использования обобщений.
Обобщение и систематизация теоретического материала по теме преобразование тригонометрических выражений учитель проводил при помощи динамической обобщающей таблицы основных тригонометрических формул и их взаимосвязей из пункта 2.5 [Приложение 3].
При изучении темы «производная» для формирования понятия производной осуществлялось индуктивное обобщение результатов решений задач из различных областей знаний (механики, геометрии, физики).
На основе сравнения и анализа решения конкретных задач был выявлен общий математический алгоритм решения для всех конкретных задач, которые приводят к новому математическому понятию – понятию производной. Все записи были оформлены в таблицу. [приложение 4]
После заполнения таблицы дается определение производной: производной функции f в точке х0 называется предел отношения приращения функции к вызвавшему его приращению аргумента, вычисленный при условии, что приращение аргумента стремится к нулю, если этот предел существует и конечен.
Понятие производной позволило сформулировать другие понятия: мгновенной скорости тела («мгновенная скорость есть производная пути по времени»), углового коэффициента касательной к графику дифференцируемой функции («угловой коэффициент производная функции в этой точке f (х0 )»), мгновенной силы тока («мгновенная сила тока есть производная количества электричества по времени»).
При таком подходе учащиеся смогли осознать появление понятия и усвоить механический, геометрический, физический смысл производной, а так же научиться решать разнообразные задачи на приложения производной.
При изучении этой же темы проводилось обобщение решения конкретной задачи на отыскание наибольшего и наименьшего значения до метода решения класса задач на оптимизацию.
Для этого была выбрана конкретная задача, ее решение оформлялось в таблицу, состоящую из двух столбцов [приложение 5]. В левом столбце – решение конкретной задачи, в правом – решение обобщенной задачи.
Задача: сумма двух целых чисел равна 24. Найдите эти числа, если известно, что их произведение принимает наибольшее значение [25, №949а].
Таким образом был выведен общий метод решения задач на отыскание наибольшего и наименьшего значения.
Составленная схема решения задач на оптимизацию сравнивалась со схемой решения алгебраических текстовых задач и был сделан вывод, текстовые задачи алгебры и начал анализа решаются по одной схеме
Из решения данной конкретной задачи так же можно вывести следующее обобщение: «произведение двух чисел, если известна их сумма, будет наибольшим, если эти числа равны ».
Обобщение как метод решения задач по индукции использовалось при выведении формулы площади боковой поверхности правильной n‑угольной призмы.
Вначале выводилась формула площади боковой поверхности правильной треугольной призмы.
Так как S бок = P осн * h , то для правильной треугольной призмы будет выполняться: S бок = 3*а* h , где а – сторона правильного треугольника, находящегося в основании призмы.
Далее формула обобщалась до формулы площади боковой поверхности правильной n‑угольной призмы.
Так, S бок = n *а* h , где а – сторона правильного n‑угольника, находящегося в основании призмы.
Все записи оформляем в таблицу [приложение 6].
Выведенная таким образом формула более понятна учащимся и сразу определяется класс задач, к которым она применима.
Обобщение как метод решения задач в «общем виде» был осуществлен при изучении темы «Многогранники» на уроке «Решение задач на призму», с целью показать, как иногда бывает более удобно решить задачу в общем виде, а потом подставить конкретные значения [Приложение 7].
Был сделан вывод, что решение задачи в общем виде и последующая подстановка числовых данных короче и производится быстрее по времени, так же яснее просматривается план решения задачи.
В результате апробации было установлено, что использование методических рекомендаций позволило повысить познавательную активность учащихся и результативность решения задач, что подтверждено рецензией учителя проводившего опытное преподавание.
Выводы по второй главе.
Таким образом обобщения при обучении решению задач являются эффективным средством поиска решения задачи и овладения общими методами решения задач.
Индуктивные обобщения при решении математических задач используются для вывода новых методов решения задач, перехода от одних методов решения задач к более общим, применимым к решению широкого класса задач. Так же индуктивные обобщения подходов к решению задачи их систематизация помогают в создании системы советов, полезных в процессе отыскания решения задачи.
Сами обобщения могут являться методом решения класса задач. При использовании обобщения как метода решения задач «по индукции» необходимо уметь выделять частные случаи. Полезно обучать школьников решению задач в общем виде, так как часто обобщенную задачу решить легче, чем конкретную задачу.
Обобщения приводят в возникновению новых задач. Необходимо проводить анализ задач и их решений, а так же обобщенных задач и их решений, при этом учащиеся могут сами составлять новые задачи, осуществляя замену части данных другими при сохранении искомых, добавляя новые заключения или обобщая искомые.
Введение понятий и теорем с помощью обобщения задач улучшает понимание вводимого знания, учащиеся сами осознают, как получили и для чего нужно новое знание, определяют его место в системе других понятий или теорем.
Обобщающие таблицы служат для проведения сравнения и анализа математических задач и их решений, при систематизации способов и методов решения задач, при составлении системы советов для поиска решения задач, при выводе понятий и обобщении материала, используемого при решении задач.
В результате проведения опытного преподавания было выявлено положительное влияние осуществления обобщений на результативность обучения школьников решению задач.
В данной работе рассмотрены обобщения при обучении решению математических задач в курсе средней (полной) школы.
Цель работы достигнута, поставленные задачи выполнены.
В работе были рассмотрены обобщения при обучении методам решения математических задач, обобщение как метод решения математических задач, обобщение как источник новых математических задач, так же обобщения задач ведущие к формированию математических понятий и теорем.
Так же была показана роль таблиц как средства обобщения при обучении решению математических задач.
Опытное преподавание подтвердило выдвинутую гипотезу: если на уроках математики организовать процесс обучения решению задач в соответствии с предложенными методическими рекомендациями, то это позволит повысить результативность обучения школьников решению задач.
1. Атанасян, Л.С. Геометрия 7–9 [Текст]: учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина. – М.: Просвещение. 1996. – 336 с.
2. Атанасян, Л.С. Геометрия 10–11 [Текст]: учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина. – М.: Просвещение. 1997. – 256 с.
3. Балк, Г.Д. О применении эвристических приемов в школьном преподавании математики [Текст] / Г.Д. Балк // Математика в школе. – 1969. – №5. – С. 21 – 28.
4. Бернштейн, М.С. Задачи на доказательство в курсе геометрии [Текст] / М.С. Бернштейн // Математика в школе. -1941. – №4. – С. 19–30.
5. Богушевский, К.С. Из писем и заметок читателей [Текст] / К.С. Богушевкий // Математика в школе. -1952. – №5. – С. 60–72.
6. Болтянский, В.Г. Анализ – поиск решения задач [Текст] / В.Г. Болтянский // Математика в школе. – 1974. – №1. – С. 34 – 40.
7. Выготский, Л.С. Избранные педагогические исследования[Текст] / Л.С. Выготский, Л.С. – М.:Изд-во АПНРСФСР, 1956. – 519 с.
8. Горский, Д.П. Краткий словарь по логике [Текст] / Д.П. Горский, А.А. Ивин, А.Л. Никифоров; Под ред. Д.П. Горского. – М.: Просвещение, 1991. – 208 с.
9. Горский, Обобщение и познание Д.П. Горский. – М.: Мысль. 1985. – 208 с.
10. Груденов, Я.И. Совершенствование методики работы учителя математики [Текст]: кн. для учителя / Я.И. Груденов. – М.: Просвещение, 1990. – 224 с.
11. Дорофеев, Г.В. Обобщение метода интервалов [Текст] / Г.В. Дорофеев // Математика в школе. – 1969. – №З.-С. 39–44.
12. Зильберберг, Н.И. Урок математики [Текст]: подготовка и проведение: кн. для учителя / Н.И. Зильберберг. – М.: Просвещение; Учеб. лит., 1995. – 178 с.
13. Изаак, Д.Ф. Обобщение задач по геометрии [Текст] / Д.Ф. Изаак // Математика в школе. – 1983. – №2. – С. 55 – 57.
14. Канин, Е.С. Заключительный этап решения учебных задач [Текст] / Е.С. Канин, Ф.Ф. Нагибин // Преподавание алгебры и геометрии в школе / сост. О.А. Боковнев. – М., 1982. – С. 131–139.
15. Канин, Е.С. Учебные математические задачи [Текст]: учеб. пособие / Е.С. Канин. – Киров: Изд – во Вят. ГГУ, 2003. – 191 с.
16. Кретинин, О.С. формирование приемов обобщения и специализации в 5 классе [Текст] / О.С. Кретинин // Математика в школе. – 1972. – №2. – С. 28 – 30.
17. Кузнецова, Алгебра. 9 кл [Текст]:сборн. зад. для проведения письм. экз. по алгебре за курс осн. школы / Л.В. Кузнецова, Е.А. Бунимович, Б.П. Пигарев, С.Б. Суворова. – М.: Дрофа, 1996. – 144 с.
18. Кушнир, И.А. Об одном способе решения задач на построение [Текст] / И.А. Кушнир // Математика в школе. – 1984. – №2. – С. 22 – 25.
19. Маланюк, М.П., Гапюк, Я.Ф. Упражнения обобщающего характера в курсе алгебры 6 класса [Текст] / М.П. Маланюк, Я.Ф. Гапюк // Математика в школе. – 1984. – №2. – С. 25 – 27.
20. Малых, Е.В. Обобщения в обучении математике учащихся полной средней школы [Текст]: дисс. … канд. пед. наук. Киров. 2005.
21. Методика обобщающих повторений при обучении математике [Текст]: пособие для учителей и студентов / В.А. Далингер. – Омск: изд-во ОГПИ. 1992. – 88 с.
22. Методика преподавания математики в средней школе. Общая методика [Текст]: учеб. пособие для студентов пед. ин-ов / А.Я. Блох, Е.С. Канин; сост. Р.С. Черкасов, А.А. Столяр. – М.: Просвещение. 1985. – 336 с.
23. Методика преподавания математики в средней школе. Общая методика [Текст]: учеб. пособие для студентов физ. – мат. фак. пед. ин-ов / В.А. Оганесян, Ю.М. Колягин, Г.Л. Луканкин, В.Я. Саннинский. – М.: Просвещение. 1980. – 368 с.
24. Мордкович, А.Г. Алгебра и начала анализа. 10–11 кл. [Текст]: учеб. для общеобразоват. учреждений / А.Г. Мордкович. – М.: Мнемозина, 2003. – 375 с.
25. Мордкович, А.Г. Алгебра и начала анализа. 10–11 кл. [Текст]: задачник для общеобразоват. учреждений / А.Г. Мордкович, Л.О. Денищева, Т.А. Корешкова, Т.Н. Мишустина, Е.Е. Тульчинская; под ред. А.Г. Мордковича. – М.: Мнемозина, 2004. – 315 с.
26. Мордкович, А.Г. Беседы с учителями математики [Текст]: Концептуал. методика. Рекомендации, советы, замечания. Обучение через задачи / А.Г. Мордкович. – М.: Школа-Пресс, 1995. – 272 с.
27. Островский, А.И. Геометрия помогает арифметике [Текст] / А И. Островский, Б. А Кордемский. – М: Физматгиз, 1960. -168 с.
28. Педагогика [Текст]: учеб. пособие для студентов пед. ин-ов / Ю.К. Бабанский, В.А. Сластенин, Н.А. Сорокин; под ред. Ю.К. Бабанского. 2 – е изд., доп. и перераб. – М.: Просвещение, 1988. – 479 с.
29. Педагогический энциклопедический словарь [Текст] / гл. ред. Б.М. Бим – Бад. – М: Большая Российская энциклопедия, 2002. – 528 с.
30. Пойа, Д. Как решать задачу [Текст]: пер. с англ. / Д. Пойа. – М.: Учпедгиз, 1959. – 216 с.
31. Пойа, Д. Математика и правдоподобные рассуждения [Текст] / Д. Пойа. – М.: Наука, 1975. – 464 с.
32. Пойа, Д. Математическое открытие [Текст] / Д. Пойа. – М.: Наука, 1970. – 452 с.
33. Понарин, Я.П. Геометрия [Текст]: учебное пособие / Я.П. Понарин. – Ростов-на-Дону: Феникс, 1997. – 512 с.
34. Психологический словарь / под ред. В.В. Давыдова, А.В. Запорожца, Б.Ф. Ломова; науч. – исслед. ин-т общей и педагогической психологии АПН СССР. – М.: Педагогика, 1983. – 448 с.
35. Родионов, М.А. Теория и методика формирования мотивации учебной деятельности школьников в процессе обучения математике [Текст]: дисс. … докт. пед. наук. – Саранск, 2001.
36. Розенфельд, Д.И. Об ознакомлении учащихся с методом обобщения [Текст] /Д.И. Розенфельд // Математика в школе. – 1965. – №1. – С. 41–43
37. Рубинштейн, С.Л. Основы общей психологии [Текст] / С.Л Рубинштейн. – СПб.: Питер Ком, 1998 – 688 с.
38. Саранцев, Г.И. Общая методика преподавания математики [Текст]: учеб. пособие для студентов мат. спец. пед. вузов и университетов / Г.И. Саранцев. – Саранск: Тип. «Крас. Окт.», 1999. – 208 с.
39. Семенов, Е.Е. Об одном приеме обучения учащихся обобщению и конкретизации [Текст] / Е.Е. Семенов // Математика в школе. – 1976. – №2. – С. 55 – 57.
40. Философская энциклопедия [Текст].Т4.-М.:Современная энциклопедия, 1967. – 519 с.
41. Философский энциклопедический словарь [Текст].Т4.-М.:Современная энциклопедия, 1983. – 446 с.
42. Фридман, Л.М., Турецкий Е.Н. Как научиться решать задачи [Текст]: кн. для учащихся ст. классов сред. шк./ Л.М. Фридман, Е.Н. Турецкий. – 3‑е изд., дораб. – М.: Просвещение, 1989. -192 с.
43. Эрдниев, П.М. Укрупнение дидактических едениц в обучении метематике[Текст]: кн. для учителя / П.М. Эрдниев, Б.П. Эрдниев. – М.: Просвещение, 1986. – 255 с.
| Действительные числа | Векторы |
| 1. Существуют отношения ра венства и неравенства | 1. Существуют отношения ра венства и неравенства |
| 2. Есть ноль | 2. Есть нулевой вектор |
| 3. Существуют противоположные числа a + (– a ) = 0 | 3. Существуют противоположные векторы: 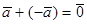 |
| 4. Определены действия сложения и вычитания чисел. Результат – число | 4. Определены действия сложения и вычитания векторов. Результат – вектор. |
| 6. Определены действия умножения и деления чисел. Результат – число. Делить на 0 нельзя | |
| 8. Существует взаимно однозначное соответствие между множеством действительных чисел и точками координатной прямой | 8. Существует взаимно однозначное соответствие между множеством векторов и точками координатной плоскости |
9. 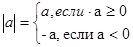 | 9. 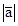 – длина вектора – длина вектора 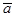 |
| 10. Направление на прямой | 10. Направление на плоскости |
| Векторы в геометрии | Векторы в физике |
| Вектор – направленый отрезок | Вектор – направленый отрезок: сила, скорость, ускорение, момент силы и т.п. |
| Скалярное умножение векторов | |
| Вычисление длины лектора | Нахождение значения равнодействующей силы, скорости и др. |
| Разложение вектора по координатным осям или по двум данным векторам | Разложение сил, скоростей, других векторных величин по координатным осям или двум данным векторам |
| Нулевой вектор | Сумма сил по замкнутому многоугольному контуру; сумма сил приложенных к центру тяжести фигуры |
| Компланарные вектора | Силы, скорости, ускорения и др., действующие в одном или противоположных направлениях |
| Некомпланарные векторы | Физические векторные величины, направленные друг к другу под углом 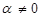 |
| Задача о скорости движения (механика) | Задача о касательной к графику функции (геометрия) | Задача о мгновенной силе электрического тока (физика) | общий алгоритм решения этих задач |
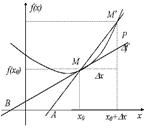
| Найти мгновенную скорость движения тела в момент времени t . | Дан график функции f = f ( x ) и точка М(х0 , f ( x 0 )) на нем. В этой точке к графику проведена касательная (предположим что существует). Найти угловой коэффициент касательной. | Для цепи переменного тока определить силу тока в данный момент времени | Нахождение производной функции в заданной точке. |
| Обозначим зависимость пути от времени как функцию S=S(t). | Рассмотрим зависимость количества электричества, протекающего через поперечное сечение проводника за время tкак функцию Q=Q(t) | Выбираем некоторую функцию f = f ( x ). | |
зафиксируем какой то момент времени t, дадим аргументу t приращение 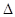 t и рассмотрим ситуацию в момент времени t и рассмотрим ситуацию в момент времени | Зафиксируем х0 и придадим приращениеаргументу 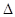 х . Получим точку х . Получим точку 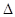 х+х0 х+х0 | Зафиксируем х0 , придадим приращениеаргументу 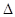 х . Получим точку х . Получим точку 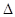 х+х0 х+х0 | |
Найдем S(t), S (t+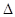 t) и вычислим приращение функции S (t+ t) и вычислим приращение функции S (t+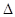 t) – S(t)= t) – S(t)= 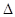 S. S. | Найдем f ( x 0 ), f ( x 0 +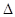 x ) и вычислим приращение функции f ( x 0 + x ) и вычислим приращение функции f ( x 0 +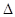 x ) – f ( x 0 )= x ) – f ( x 0 )= 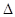 f . Через точки М(х0 , f ( x 0 ) и М’ ( x 0 + f . Через точки М(х0 , f ( x 0 ) и М’ ( x 0 +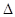 x , f ( x 0 + x , f ( x 0 +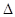 x )) проведем секущую к кривой MM ’. x )) проведем секущую к кривой MM ’. | Найдем Q(t0 ), Q(t0 + 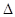 t ) и приращение количества электричества t ) и приращение количества электричества 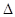 Q = Q(t0 + Q = Q(t0 +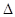 t) – Q(t0 ) t) – Q(t0 ) | Найдем f ( x 0 ), f ( x 0 +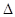 x ), приращение функции f ( x 0 + x ), приращение функции f ( x 0 +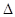 x ) – f ( x 0 )= x ) – f ( x 0 )= 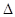 f . f . |
Найдем среднюю скорость vср .= 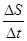 | Тогда угловой коэффициент секущей будет 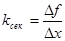 | Найдем среднюю силу тока I ср .=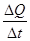 | Составим отношение 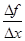 |
Учитывая, что касательная к кривой в точке М есть предельное положение секущей то при 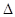 х->0 M ’-> M . Получаем: х->0 M ’-> M . Получаем: 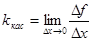 | определяем условие существования предела 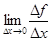 | ||
| Это и есть мгновенная скорость движения тела. | Это и есть угловой коэффициент касательной | Это есть определение мгновенной силы тока. | Тогда предел 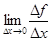 есть производная функции f = f ( x ) в точке x 0 и обозначаетсяf ’ ( x 0 ) есть производная функции f = f ( x ) в точке x 0 и обозначаетсяf ’ ( x 0 ) |
Задача: сумма двух целых чисел равна 24. Найдите эти числа, если известно, что их произведение принимает наибольшее значение [25, №949а].
| Решение конкретной задачи | Решение обобщенной задачи | |
| сумма двух целых чисел равна 24. Найдите эти числа, если известно, что их произведение принимает наибольшее значение. | По исходным данным найти наибольшее или наименьшее значение какой-либо функции | |
| 1. Введем переменные: первое число равно х, второе – 24‑х | 2. Ввести переменную, выразить через нее все остальные переменные задачи | |
| 2. Произведением двух чисел является функция P(x)=x(24‑х) | 3. Составить функцию для исследования на экстремум | |
| 3. Так как х – целое число, а сумма двух чисел равна 24, то 0 Pосн = 3*a, где а – сторона правильного треугольника, находящегося в основании призмы 1) h– высота правильной n‑угольной призмы, в данном случае ребро призмы 2) Pосн – периметр правильной n‑угольной призмы В основании правильный n‑угольник -> Pосн = n*a, где а – сторона правильного n‑угольника, находящегося в основании призмы | ||
| формула площади боковой поверхности призмы необходимого вида | Sбок = 3*а*h | Sбок = n*а*h |
Задача: Основанием наклонной призмы ABCA 1 B 1 C 1 является равнобедренный треугольник ABC , в котором AC = AB =13 см, BC =10 см, а боковое ребро призмы образует с плоскостью основания угол 45 0 . Проекцией вершины А1 является точка пересечения медиан треугольника ABC . Найдите площадь грани CC 1 B 1 B » [2, №228].
Вначале задача была решена по этапам. Этим была показана громоздкость решения и смотивировано отыскание решения задачи в «общем виде» с последующей подстановкой числовых данных.
1. Решение по этапам.
1) Так как треугольник ABC – равнобедренный, то AK является медианой и высотой. Тогда AK =
2) по свойству медианы

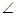
4) Тогда AA1 =
то SBB 1 CC 1 =10*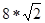
Ответ: SBB 1 CC 1 =
2. Решение задачи в общем виде с последующей
подстановкой данных короче и быстрее.
SBB 1 CC 1 = BB 1 * BC ; AA 1 = BB 1 = CC 1, тоSBB 1 CC 1 = AA 1 * BC =
| Задача 1 | Задача 2 | Задача 3 | Метод | ||||||||||||||||||||||||||||
| Построить равнобедренный треугольник ABC (b=c) по а, hb . | Построить треугольник ABC по a, mb , mc | Построить ромб ABCD по диагонали BD и высоте ВН | Построение фигуры с помощью вспомогательного треугольника | ||||||||||||||||||||||||||||
| Вопросы и советы для усвоения содержания задачи | ||||||||||||||||||||||||||||
| Вопросы и советы для составления плана решения задачи | ||||||||||||||||||||||||||||
| Советы для реализации плана решения задачи | ||||||||||||||||||||||||||||
| шаги | Задача №1: докажите, что середина гипотенузы прямоугольного треугольника равноудалена от всех его вершин. | Общий алгоритм | Задача №2: докажите, что сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей. |
| 1 | Рассмотрим треугольник ABC, угол С-прямой. М – середина гипотенузы AB. Введем прямоугольную систему координат так, что С-центр, CB‑на оси х, СA – на оси у. | Вводим прямоугольную систему координат так, чтобы одна из точек фигуры являлась центром, и хотя бы одна сторона лежала на какой-либо оси. | АBCD‑данный параллелограмм. Введем прямоугольную систему координат так, что А-центр, AD – на оси х. |
| 2 | Обозначим: BC=a, AC=b, тогдавершиныC (0,0), B (a, 0), A (0, b), М (a/2, b/2) | Обозначаем координаты точек во введенной системе координат. | Обозначим: AD=BC=a, тогдавершиныA (0,0), B (b, c), D (a, 0), C (a+b, c) |
| 3 | Используя нужную формулу, составляем равенство, которое необходимо доказать, и доказываем его в координатной форме. | ||
| MA=MB=MC, что и требовалось доказать | Запись ответа | Таким образом, AB 2 +BC 2 +CD 2 +DA 2 =AC 2 +BD 2 , что и требовалось доказать |
| № | Задача | Решение задачи | Вывод |
| 1 | Определить вид четырехугольника ABCD его вид, если известно, что 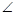 A+ A+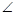 B=180 0 , B=180 0 , 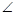 A=смежному с A=смежному с 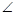 D по продолжению AD и имеет место равенство: AB+CD=BC+AD D по продолжению AD и имеет место равенство: AB+CD=BC+AD | Определение: параллелограмм, у которого все стороны равны называется ромбом | |
| 2 | Дан, параллелограмм ABCDAB=BC=CD=AD. Доказать, что треугольник BOC– прямоугольный, где O – точка пересечения диагоналей. | Так как в параллелограмме ABCD все стороны равны, то это ромб. Задача отражает свойство ромба: диагонали ромба взаимно перпендикулярны | |
| 3 | В параллелограмме ABCD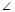 ABD= ABD=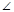 DBC, AB=a. Найти периметр параллелограмма ABCD. DBC, AB=a. Найти периметр параллелограмма ABCD. |


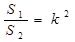 . Тогда, анализируя задачу, когда S 1 и S 2 – площади треугольников, можно сделать обобщение, когда S 1 и S 2 – площади многоугольников. Это обобщение, в свою очередь, может быть рассмотрено для конкретных многоугольников.
. Тогда, анализируя задачу, когда S 1 и S 2 – площади треугольников, можно сделать обобщение, когда S 1 и S 2 – площади многоугольников. Это обобщение, в свою очередь, может быть рассмотрено для конкретных многоугольников.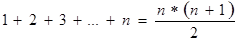
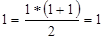
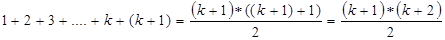
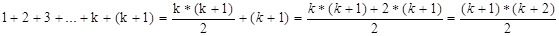

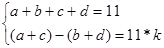



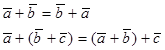
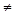 0 , если a
0 , если a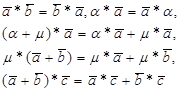

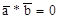 может быть при
может быть при 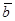
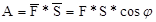
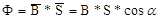 где Ф – магнитный поток,В-магнитная индукция, S– площадь контура
где Ф – магнитный поток,В-магнитная индукция, S– площадь контура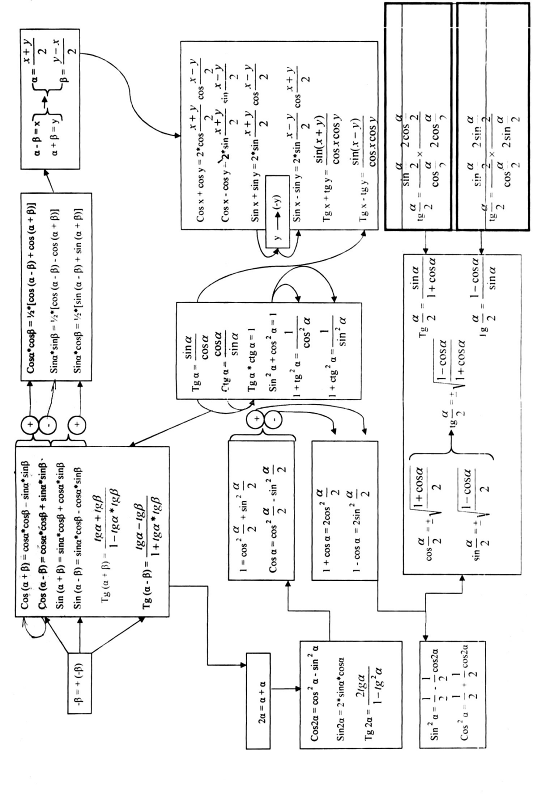
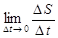
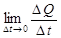
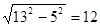
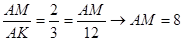
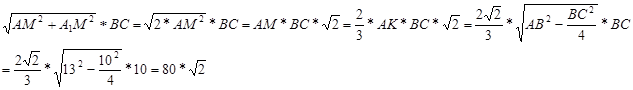
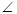 B,
B, 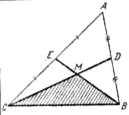
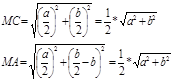
 2)
2)  1) AB=BC=CD=AD, треугольник ABC – равнобедренный.
1) AB=BC=CD=AD, треугольник ABC – равнобедренный.


