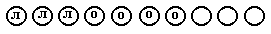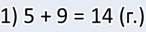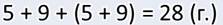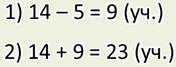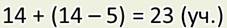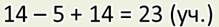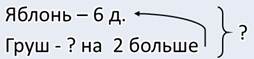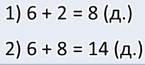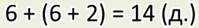Способ решения задач выражением

Способ решения задач выражением

СПОСОБЫ РЕШЕНИЯ ЗАДАЧ

Понятие “решение задачи” можно рассматривать с различных точек зрения: решение как результат, т.е. как ответ на вопрос, поставленный в задаче, и решение как процесс нахождения этого результата.

С точки зрения методики обучения решению задач на первый план выступает процесс нахождения результата, который в свою очередь, тоже можно рассматривать с различных точек зрения Во-первых, как способ нахождения результата и, во-вторых, как последовательность тех действий, который входят в тот или иной способ.

Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?

Учащиеся могут решить эту задачу, не имея никакого представления о делении и о записи этого действия, а только опираясь на свой жизненный опыт и владея счетом от 1 до 8. Для этого они отсчитывают 8 яблок, положат 2 на одну тарелку, затем 2 на другую и т.д. пока не разложат все. Посчитав количество тарелок, они ответят на поставленный вопрос. Такой способ и называется практическим или предметным. Его возможности ограничены, так как учащийся может выполнить предметные действия только с небольшим количеством предметов. Усвоив смысл действия деления и его запись, можно решить эту задачу уже не практическим, а арифметическим способом, записав равенство 8 : 2 = 4.

Для решения можно применить алгебраический способ, рассуждая при этом так: “Число тарелок неизвестно, обозначим их буквой Х. На каждой тарелке 2 яблока, значит число всех яблок — это 2х. Так как в условии известно, что число всех яблок 8, то можно записать уравнение 2х = 8 и решить его х = 8 : 2, х = 4”.

Задачи, в которых для ответа на вопрос нужно выполнить только одно действие, называются простыми. Если для ответа на вопрос задачи нужно выполнить два и более действий, то такие задачи называются составными. Составную задачу, так же как и простую можно решить, используя различные способы.

Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?

Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим

пойманных рыб: л — лещи, о — окуни.

Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество пойманных щук соответствует тем кругам, которые не обозначены (их З).

1) 3 + 4 = 7 (р.) — пойманные рыбы

Для ответа на вопрос задачи мы выполнили два действия.

Пусть х — пойманные щуки

Тогда количество всех рыб можно записать выражением:

3 + 4 + х — все рыбы

По условию задачи известно, что рыбак поймал всего 10 рыб.

Значит 3 + 4 + х = 10

Решив это уравнение, мы ответим на вопрос задачи.

Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.

В начальных классах используются различные формы записи решения задач по действиям, по действиям с пояснением, с вопросами, выражением.

У мальчика было 90 книг. 28 он поставил на первую полку, 12 на вторую. Остальные на третью. Сколько книг на третьей пилке?

а) решение по действиям

Ответ: 50 книг на третьей полке.

б) по действиям с пояснением

1) 28 + 12 = 40 (к.) на 1 и 2 полках вместе.

2) 90 — 10 = 50 (к.) на 3 полке.

1) Сколько книг на первой и второй полках вместе?

2) Сколько книг на третьей полке?

При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:

90 — (28 + 12) = 50 (к.)

Не следует путать такие понятие как: решение задачи различными способами (практический, арифметический графический, алгебраический), различные формы записи арифметического способа, решения задачи (по действиям, выражением по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомым, а, с следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.

Например, рассмотренную выше задачу можно решить другим арифметическим способом:

1) 90 — 28 = 62 (к.) на 2 и3 полках.

Читайте также:  Способы обвязки бусины крючком

2) 62 — 12 = 50 (к.) на 3 полке.

В качестве арифметического способа можно рассматривать и такое решение данной задачи:

1) 90 — 12 = 78 (к.) на 2 и 3 полках.

2) 78 -28 = 50 (к.) на З полке.

В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.

Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?

Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:

Ответ: 27 машин было в гараже

В альбоме для раскрашивания 48 листов. Часть альбома Коля раскрасил. Сколько листов осталось не раскрашенными, если Коля раскрасил в 2 раза больше, чем ему осталось?

Решение задачи можно оформить так:

48 : 3 = 16 (л.) Ответ: 16 листов

[../../../_private/navbar1.htm]

Источник

Способ решения задач выражением

Как показывает практика, многие студенты педагогических факультетов, а иногда и учителя начальных классов не понимают разницы между различными способами решения и различными формами записи решения задачи. Один и тот же способ решения текстовой задачи можно записать каждым из первых пяти перечисленных выше форм.

Рассмотрим возможные варианты обучения детей записи решения задачи при помощи числового выражения.

На этапе ознакомления с решением задач нового типа этот способ записи решения задачи могут использовать не все учащиеся, а лишь единицы. На данном этапе целесообразно использовать запись решения задачи по действиям с вопросами или пояснениями, либо в соответствии с составленным планом.

Если же навык решения задач данного вида отработан, то запись решения числовым выражением имеет ряд преимуществ: учащемуся требуется гораздо меньше времени на оформление задачи; появляется возможность решить за урок гораздо больше задач. Ведь не секрет, что младшие школьники пишут медленно, а запись решения задачи выражением более компактна. Кроме того, решая задачи составлением выражений, дети лучше готовятся к обучению в старших классах. Углубляются знания свойств и законов арифметических действий, представления о числовом выражении и его значении, т.е. осуществляется алгебраическая пропедевтика. В задачах с буквенными данными решение записывается только выражением.

Анализ методической литературы по вопросу обучения детей записи решения задачи составлением выражения и анализ просмотренных уроков математики в начальной школе позволил нам выделить следующие подходы к решению данного вопроса: способ последующей работы над записью решения задачи и способ поэтапной записи выражения в процессе решения задачи (названия автора).

Приведем примеры организации учебно-познавательной деятельности учащихся при их обучении записи решения задач при помощи числового выражения двумя вышеперечисленными способами.

Первый способ – способ последующей работы над записью решения задачи выражением после ее решения по действиям. Работа над решением задачи и его записью проводится в такой последовательности: учащиеся сначала решают задачу по действиям, а потом учитель предлагает составить по полученным действиям выражение.

Источник

Способы записи решения задач.
учебно-методический материал по математике

Учебный-методический материал поможет учителю при работе с текстовыми задачами на уроках математики.

Скачать:

Вложение	Размер
sposoby_zapisi_resheniya_zadach.doc	26 КБ

Предварительный просмотр:

Способы записи решения задач.

Начальный курс математики ставит своей основной целью научить младших школьников решать задачи арифметическим способом, который сводится к выбору арифметических действий, моделирующих связи между данными и искомыми величинами. Решение задач в этом случае оформляется в виде последовательности числовых равенств, к которым даются пояснения, или числовым выражением. В начальных классах используются различные формы записи решения задач арифметическим способом: по действиям; по действиям с пояснением; с вопросами; выражением.

У мальчика было 90 книг. 28 он поставил на первую полку. 12 — на вторую, остальные — на третью. Сколько книг на третьей полке?

а ) Решение по действиям:

Ответ: 50 книг на третьей полке.

б ) По действиям с пояснением:

1) 28+12=40 ( к.) — на первой и второй полках вместе,

2) 90-40=50 ( к.) — на третьей полке.

1) Сколько книг на первой и второй полках вместе?

2) Сколько книг на третьей полке?

Ответ: 50 книг на третьей полке,

При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так: 90-(28+12)=50 (к.)

Ответ: 50 книг на третьей полке.

Не следует путать такие понятия, как: решение задачи различными способами (практический, арифметический, графический, алгебраический); различные формы записи арифметического способа решения задачи (по действиям, выражением, по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомыми, а следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.

Например, рассмотренную выше задачу можно решить другим арифметическим способом:

1) 90-28 = 62 ( к.) — на второй и третьей полке,

2) 62-12 = 50 ( к.) — на третьей полке.

Ответ: 50 книг на третьей полке.

В качестве арифметического способа можно рассматривать и такое решение

1) 90-12 = 78 ( к.) — на первой и третьей полке,

2) 78-28 = 50 ( к.) — на третьей полке.

Ответ: 50 книг на третьей полке

По теме: методические разработки, презентации и конспекты

Урок математики во 2 классе «Решение задач графическим способом»

Урок развивает умение решать текстовые задачи графическим способом; развивает математическую речь, логическое мышление; воспитывает интерес к точным наукам, аккуратность, чувство товарищества, в.

Конспект урока русского языка на тему: «Выявление орфографической задачи на месте сочетаний [сн], [с\’н\’] и способы её решения.

Тема урока: «Выявление орфографической задачи на месте сочетаний [сн], ]с\’н\’] и способы её решения»Цель урока: усвоение основ орфограммНа уроке ребята узнают, что некоторые звуки руссого языка трудно .

Мастер-класс » Комбинаторные задачи и способы их решения»

ФГОС второго поколения начального общего образования определяет новые требования к уровню подготовки младших школьников, что предполагает необходимость переосмысления учителями начальной школы как сам.

Конспект урока математики по теме: «Решение задач разными способами»

Конспект урока с использованием деятельностного подхода.

Конспект урока по математике в 3 классе «Решение задач разными способами»

Конспект урока по математике в 3 классе.

Методика записи краткого условия и решения задачи.

Уроки счета для глубоко умственно отсталых связаны с формированием разнообразных умений и навыков умственной и учебной деятельности способствуют коррекции недостатков познавательной деятельности и лич.

Конспект урока математики 4 класс (система Д.Б.Эльконина – В.В.Давыдова) Тема. Анализ средств для самоконтроля при составлении краткой записи и решении задач.

Конспект урока математики 4 класс (система Д.Б.Эльконина – В.В.Давыдова)Тема. Анализ средств для самоконтроля при составлении краткой записи и решении задач.Тип урока. Урок рефлексии.Цель. Форми.

Источник

Запись решения задачи выражением

Урок 15. Математика 2 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Запись решения задачи выражением»

— Плюс. Плююююс! Ты где?

Привет, Плюс! Чего так долго? Включай скорее компьютер. Сейчас у нас будет в скайпе разговор с царицей Математикой.

— Здравствуй, Минус. Как это я забыл! Включаю.

— Здравствуйте, Дорогие Плюс и Минус!

Сегодня я хочу проверить, как вы умеете решать задачи. Я дам несколько задач и предлагаю вам устроить соревнование — кто сможет их решить быстрее, но при этом, конечно, правильно.

— Да, царица, мы Вас внимательно слушаем.

— Мы очень внимательно слушаем.

— Ну что же, приступим. Итак, вот первая задача:

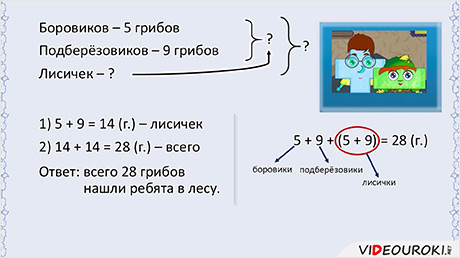
Ребята в лесу собирали грибы. Они нашли 5 боровиков, 9 подберёзовиков, а лисичек столько, сколько боровиков и подберёзовиков вместе. Сколько всего грибов нашли ребята в лесу?

Ну, Плюс и Минус, я жду вашего решения. Может быть и ребята, которые на вас смотрят, попробуют решить эту задачу.

— Всё, я готов! Могу даже объяснить, как я решал эту задачу.

Нам даны два числа: количество боровиков — их 5, и количество подберёзовиков — их 9. Но неизвестно количество лисичек. Про них сказано, что их столько, сколько боровиков и подберёзовиков вместе. А ещё неизвестно, сколько всего грибов.

В задаче два неизвестных, значит, задача составная, то есть в ней не одно действие, а два. В первом действии я узнаю, сколько лисичек.

А так как боровиков и подберёзовиков вместе столько же, сколько и лисичек, то общее количество грибов я нашёл вот так:

Ответ: всего 28 грибов нашли ребята в лесу.

— А я решал задачу другим способом. Вот посмотрите:

— Да, Минус, чувствуется, что сложение — это не твой конёк. Конечно, задачу ты решил правильно. Но при этом у тебя получилось не два, а три действия. При этом первое и второе действия повторяются. Для этой задачи такой способ записи не очень удобен. Хотя некоторые задачи действительно удобно записывать не по действиям, как это сделал я, а числовым выражением. А вот, кстати, царица Математика уже даёт нам новую задачу.

— Тихо, Плюс, слушаем!

— На уроке физкультуры присутствовало 14 мальчиков. А девочек — на 5 меньше. Сколько всего учащихся присутствовало на уроке физкультуры?

— Ну что же, начинаем решать. Ребята, и вы попробуйте с нами решать!

— Я уже решил. Вот посмотрите, в задаче известно количество мальчиков, Их 14. Но неизвестно количество девочек. Ведь сказано, что их на 5 меньше, чем мальчиков.

А в задаче надо узнать количество девочек, и только потом — сколько всего детей. Я так и узнавал:

Ответ: всего 23 учащихся присутствовало на уроке физкультуры.

— А вот я записал решение этой задачи по-другому:

И ещё можно вот так:

— Но ведь ты мне только что говорил, что такой способ решения неудобен! Зачем же ты решил задачу другим способом — записью выражения.

— В первой задаче он действительно был неудобен, а в этой — очень даже удобен. Во-первых, это не другой способ решения задачи. Посмотри, в моём решении есть те же действия, что и в твоём, и даже в той же последовательности.

Ты первым действием узнаёшь, сколько девочек, и я тоже. Ведь это действие я записал в скобках. А то, что записано в скобках, всегда выполняется первым.

Во втором действии к 14 прибавляем полученное в первом действии число 9. А в этой записи слагаемые меняются местами — к 9 прибавляется 14.

И получается, что это не другой способ решения задачи — ведь все действия одинаковы, а другой способ записи решения. Ты решал по действиям, а я — выражением. Способ решения одинаковый, а способ записи этого решения — разный. Но посмотри, моя запись получилась короче. В ней нет номеров действий и пояснений. Поэтому такая запись помогает экономить и время, и бумагу.

— Ты, Плюс, как всегда. Все тебе надо складывать да экономить. Хотя, наверное, ты прав. Эта запись действительно удобная. А хотелось бы и мне попробовать такую запись задачи выражением.

Ваше величество, госпожа королева. Не могли бы Вы задать нам ещё одну задачу?

— Ну что же, слушайте:

В моём саду растёт 6 яблонь. А груш на 2больше. Сколько всего яблонь и груш растёт в моём саду?

Я хочу видеть у вас оба способа записи решения — и по действиям, и выражением.

— Ну вот что у меня получилось. Прежде, чем узнать, сколько всего яблонь и груш, необходимо узнать, сколько груш. Ведь нам это неизвестно. Сказано, что их на 2 больше, чем яблонь.

Значит, в саду царицы растёт 14 яблонь и груш.

А вот как получилась запись выражением:

Сначала я нашёл, количество груш. Но, так как это действие стоит не в начале записи, я выделил его скобками. А потом нашёл сумму чисел. Ответ такой же, как и при записи по действиям — 14.

— Хорошо. Задача решена, верно. А теперь расскажите, чему вы научились.

— Можно я начну первый.

Записывать решение задачи можно по действиям и выражением.

— При записи по действиям мы пишем номер действия и пояснения к каждому действию, а при записи выражением только пояснение к значению записанного выражения.

— При записи выражения первое действие часто записываем в скобках, и конечно, не забываем записать ответ задачи.

— Ну что же, молодцы, Плюс и Минус. Вы справились с заданием. И сейчас вы можете пойти погулять в мой сад и полакомиться яблоками и грушами.

Источник