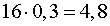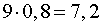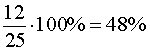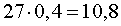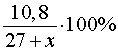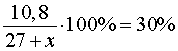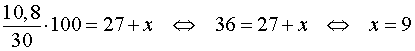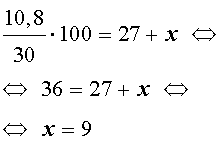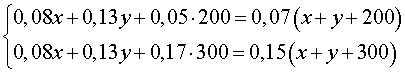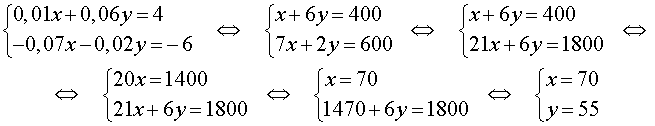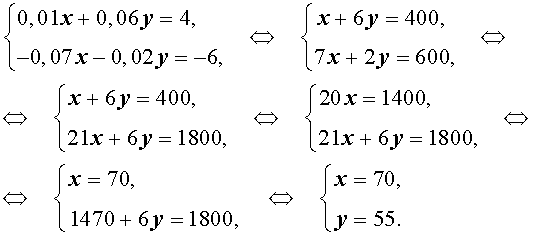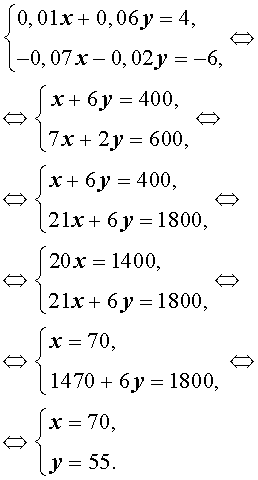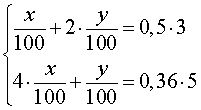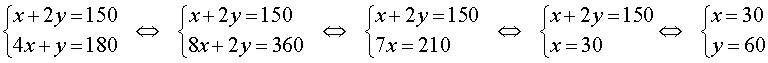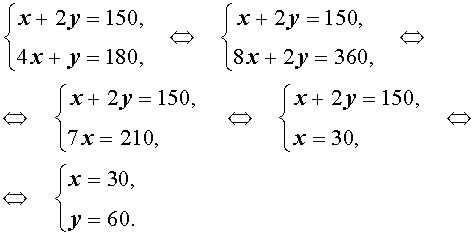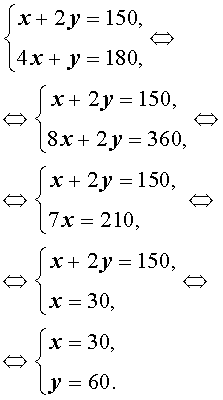Различные способы решение задач на смеси, сплавы, растворы
материал для подготовки к егэ (гиа) по алгебре (9, 11 класс) на тему
Задачи на смеси, сплавы, растворы вызывают у учащихся общеобразовательных классов затруднения. Самостоятельно справиться с ними могут немногие. Задачи данного типа, ранее встречающиеся практически только на вступительных экзаменах в ВУЗы и олимпиадах, сейчас включены в КИМы для подготовки и проведения экзамена по математике за курс основной школы. Эти задачи, имеющие практическое значение, являются также хорошим средством развития мышления учащихся. Поэтому на сегодняшний день тема решений таких задач является актуальной.
Скачать:
| Вложение | Размер |
|---|---|
| razlichnye_sposoby_reshenie_zadach_na_smesi_splavy_rastvory.rar | 2.48 МБ |
Предварительный просмотр:
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 46»
Различные способы решения задач на смеси, сплавы, растворы.
Автор: Гревцева Елена Владимировна
Глава 1. Теоретические основы решения задач «на смеси,
Глава 2. Типы задач «на смеси сплавы, растворы».
В современном мире множество отраслей, связанных с химией, например такие, как пищевая, фармацевтическая, тяжёлая промышленность, медицина, фармакология и т.д. Однако все они связаны не только с химией, но и с математикой, так как приходится решать задачи на процентное содержание в продукте питания, металле, лекарстве, косметике и т.д. тех или иных веществ.
Задачи на смеси, сплавы, растворы при первом знакомстве с ними вызывают у учащихся общеобразовательных классов затруднения. Самостоятельно справиться с ними могут немногие. Задачи данного типа, ранее встречающиеся практически только на вступительных экзаменах в ВУЗы и олимпиадах, сейчас включены в КИМы для подготовки и проведения экзамена по математике за курс основной школы. Эти задачи, имеющие практическое значение, являются также хорошим средством развития мышления учащихся. Поэтому на сегодняшний день тема решений таких задач является актуальной.
Итак, объект исследования: математика.
Предмет исследования: задачи «на смеси, сплавы, растворы»
Цель работы: помочь учащимся 11 классов успешно сдать выпускной экзамен.
Глава 1. Теоретические основы решения задач «на смеси, сплавы, растворы».
Чтобы лучше понимать условия задач, необходимо знать следующие понятия:
- Все получающиеся сплавы или смеси однородны.
- При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов.
- Процент — одна сотая любого вещества.
- Производительность объекта — скорость работы
- Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси. Она показывает долю вещества в растворе.
- Это отношение может быть выражено либо в дробях, либо в процентах.
- Сумма концентраций всех компонент, составляющих смесь, равна единице.
Глава 2. Типы задач «на смеси сплавы, растворы». Способы их решения.
Все задачи на «смеси, сплавы, растворы» можно разделить на три типа:
- на вычисление концентрации;
- на вычисление количества чистого вещества в смеси (или сплаве);
- на вычисление массы смеси (сплава).
Существуют следующие способы решения задач:
- с помощью таблиц;
- с помощью схемы;
- старинным арифметическим способом;
- алгебраическим способом;
- с помощью графика;
- с помощью формулы.
Алгоритм решения задачи на сплавы, растворы и смеси:
- Изучить условия задачи;
- Выбрать неизвестную величину (обозначить ее буквой);
- определить все взаимосвязи между данными величинами;
- Составить математическую модель задачи (выбрать способ решения задачи, составить пропорцию или уравнение относительно неизвестной величины) и решить ее;
- провести анализ результата.
Глава 3. Рассмотрим несколько задач и решим их различными способами.
Задача 1 . Сколько нужно добавить воды в сосуд, содержащий 200 г
70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?
Источник
Задачи на смеси, сплавы и растворы
 Концентрация (процентное содержание) вещества Концентрация (процентное содержание) вещества |
 Примеры решения задач на смеси, сплавы и растворы Примеры решения задач на смеси, сплавы и растворы |
Концентрация (процентное содержание) вещества
Рассмотрим смесь (сплав, раствор) из нескольких веществ.
Определение 1. Концентрацией (процентной концентрацией, процентным содержанием) вещества A в смеси (сплаве, растворе) называют число процентов pA , выраженное формулой
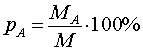 | (1) |
где MA – масса вещества A в смеси (сплаве, растворе), а M – масса всей смеси (сплава, раствора).
Часто в задачах на растворы указаны не массы входящих в них веществ, а их объёмы. В этом случае вместо формулы (1) для концентрации (процентной концентрации, процентного содержания) вещества A в растворе используется формула
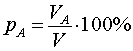 | (2) |
где VA , – объём вещества А в растворе, а V – объем всего раствора.
Определение 2 . Формулу (1) называют формулой для массовой концентрации вещества A в смеси (сплаве, растворе), а формулу (2) – формулой для объёмной концентрации вещества A в растворе.
При решении задач считается, что при слиянии нескольких растворов (сплавов) масса и объем полученной смеси равны сумме масс и объемов смешиваемых компонентов соответственно.
Приёмы, используемые при решении задач на массовые концентрации смесей (сплавов, растворов), а также при решении задач на объёмные концентрации растворов, являются общими, что мы и увидим при решении следующих типовых задач
Примеры решения задач на смеси, сплавы и растворы
Задача 1 . Смешали 16 литров 30% раствора кислоты в воде с 9 литрами 80% раствора кислоты в воде. Найти концентрацию полученного раствора кислоты в воде.
Решение . В 16 литрах 30% раствора кислоты в воде содержится
литров кислоты. В 9 литрах 80% раствора кислоты в воде содержится
литров кислоты. Поэтому в смеси этих растворов содержится
литров кислоты. Поскольку полученный в результате смешивания раствор имеет объем
литров, то концентрация кислоты в этом растворе равна
Задача 2 . Имеется 27 килограммов смеси цемента с песком с 40% содержанием цемента. Сколько килограммов песка нужно добавить в эту смесь, чтобы процентное содержание цемента в ней стало 30% ?
Решение . Обозначим буквой x количество килограммов песка, которые нужно добавить в смесь. Поскольку в 27 килограммах смеси с 40% содержанием цемента содержится
килограммов цемента, а после добавления x килограммов песка масса смеси станет равной
килограммов, то после добавления песка процентное содержание цемента в получившейся смеси будет составлять
По условию задачи
Ответ . 9 килограммов.
Задача 3 . Смешав 8% и 13% растворы соли и добавив 200 миллилитров 5% раствора соли, получили 7% раствор соли. Если бы вместо 200 миллилитров 5% раствора соли добавили 300 миллилитров 17% раствора соли, то получили бы 15% раствор соли. Сколько миллилитров 8% и 13% растворов соли использовали для получения раствора?
Решение . Обозначив буквой x массу 8% раствора соли, а буквой y – массу 13% раствора соли, рассмотрим рисунки 1 и 2.
| x мл | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| + | y мл | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| + | 200 мл | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | (x + y + 200) мл | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||