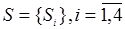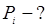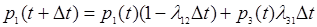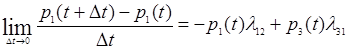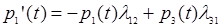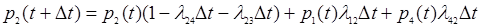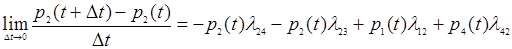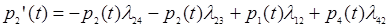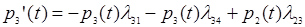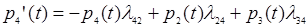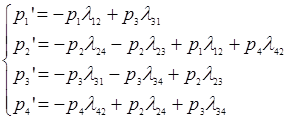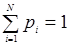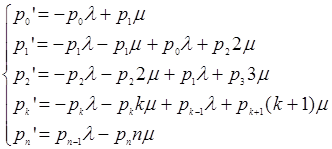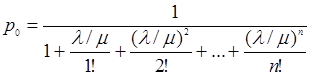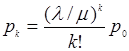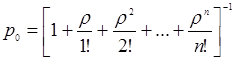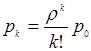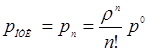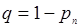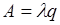Способ решения уравнения колмогорова

Уравнения Колмогорова.
Предельные вероятности состояний

Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями ; так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока «окончаний ремонтов» первого узла и т.п.

Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния: .

Вероятностью i-го состояния называется вероятность того, что в момент система будет находиться в состоянии . Очевидно, что для любого момента сумма вероятностей всех состояний равна единице:

Рассмотрим систему в момент и, задав малый промежуток , найдем вероятность того, что система в момент будет находиться в состоянии . Это достигается разными способами.

1. Система в момент с вероятностью находилась в состоянии , а за время не вышла из него.

Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной . А вероятность того, что система не выйдет из состояния , равна . Вероятность того, что система будет находиться в состоянии по первому способу (т.е. того, что находилась в состоянии и не выйдет из него за время ), равна по теореме умножения вероятностей:

2. Система в момент с вероятностями (или ) находилась в состоянии или и за время перешла в состояние .

Потоком интенсивностью (или — с- рис. 1) система перейдет в состояние с вероятностью, приближенно равной (или ). Вероятность того, что система будет находиться в состоянии по этому способу, равна (или ).

Применяя теорему сложения вероятностей, получим

Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную (обозначим ее для простоты ):

Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.

Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:

Сформулируем правило составления уравнений Колмогорова . В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).

В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).

Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии , т.е. при начальных условиях .

Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени . Особый интерес представляют вероятности системы в предельном стационарном режиме , т.е. при , которые называются предельными (или финальными) вероятностями состояний.

В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.

Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии . Например, если предельная вероятность состояния , т.е. , то это означает, что в среднем половину времени система находится в состоянии .

Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:

Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом , согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.

Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при

Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или

(Здесь мы вместо одного «лишнего» уравнения системы (10) записали нормировочное условие (8)).

Решив систему (11), получим , т.е. в предельном, стационарном режиме система в среднем 40% времени будет находиться в состоянии (оба узла исправны), 20% — в состоянии (первый узел ремонтируется, второй работает), 27% — в состоянии (второй узел ремонтируется, первый работает) и 13% времени — в состоянии (оба узла ремонтируются)

Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).

Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел — . В то же время первый узел находится в ремонте в среднем долю времени, равную , а второй узел — . Поэтому средний чистый доход в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен

Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока «окончаний ремонтов» каждого узла, т.е. теперь и система линейных алгебраических уравнений (10), описывающая стационарный режим системы , вместе с нормировочным условием (8) примет вид:

Решив систему, получим .

Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход в единицу времени:

Так как больше (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.

Процесс гибели и размножения

В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения . Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.

Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.

Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния возможны переходы только либо в состояние , либо в состояние .

Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или .

По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).

В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния

для состояния имеем , которое с учетом (12) приводится к виду

Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:

к которой добавляется нормировочное условие

При анализе численности популяций считают, что состояние соответствует численности популяции, равной , и переход системы из состояния в состояние происходит при рождении одного члена популяции, а переход в состояние — при гибели одного члена популяции.

Решая систему (14), (15), можно получить

Легко заметить, что в формулах (17) для коэффициенты при есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния , а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния .

Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.

Источник

Уравнения Колмогорова для вероятностей состояний. Финальные вероятности состояний

Рассматривая марковские процессы с дискретными состояниями и непрерывным временем, нам удобно будет представлять себе, что все переходы системы S из состояния в состояние происходят под действием каких-то потоков событий (поток вызовов, поток отказов, поток восстановлений и т.д.). Если все потоки событий, переводящие систему S из состояния в состояние,- простейшие, то процесс, протекающий в системе, будет марковским. Это и естественно, так как простейший поток не обладает последействием: в нем «будущее» не зависит от «прошлого».

Если система S находится в каком-то состоянии Si, из которого есть непосредственный переход в другое состояние Sj (стрелка, ведущая из Si в Sj на графе состояний), то мы себе это будем представлять так, как будто на систему, пока она находится в состоянии Si действует простейший поток событий, переводящий ее по стрелке Si → Sj. Как только появится первое событие этого потока, происходит «перескок» системы из Si в Sj.

Для наглядности очень удобно на графе состояний у каждой стрелки проставлять интенсивность того потока событий, который переводит систему по данной стрелке. Обозначим λij интенсивность потока событий, переводящего систему из состояния Si в Sj. На рис. 4.7 дан граф состояний с проставленными у стрелок интенсивностями (мы будем называть такой граф размеченным).

Рис. 4.7. Размеченный граф состояний

Построим размеченный граф состояний для технического устройства из двух узлов. Состояния системы:

S0 — оба узла исправны,

S1 — первый узел ремонтируется, второй исправен,

S2 — второй узел ремонтируется, первый исправен,

S3 — оба узла ремонтируются.

Интенсивности потоков событий, переводящих систему из состояния в состояние, будем вычислять, предполагая, что среднее время ремонта узла не зависит от того, ремонтируется ли один узел или оба сразу. Это будет именно так, если ремонтом каждого узла занят отдельный специалист. Найдем все интенсивности потоков событий, переводящих систему из состояния в состояние. Пусть система находится в состоянии S0. Какой поток событий переводит ее в состояние S1? Очевидно, поток отказов первого узла. Его интенсивность λ1 равна единице, деленной на среднее время безотказной работы первого узла. Какой поток событий переводит систему обратно из S1 в S0? Очевидно, поток «окончаний ремонтов» первого узла. Его интенсивность μ1 равна единице, деленной на среднее время ремонта первого узла. Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем стрелкам графа рис. 4.7.

Имея в своем распоряжении размеченный граф состояний системы, легко построить математическую модель данного процесса.

В самом деле, пусть рассматривается система S, имеющая n возможных состояний S1, S2. Sn. Назовем вероятностью i-го состояния вероятность pi(t) того, что в момент t система будет находиться в состоянии Si. Очевидно, что для любого момента сумма всех вероятностей состояний равна единице:

Источник

Методика вывода уравнений Колмогорова

-интенсивность перехода

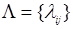
1. Найдем вероятность того, что в момент времени t система

находится в состоянии S1. Придадим t малое приращение Dt и

определим, что система в момент времени t+Dt находится в состоянии S1.

2. Найдем вероятность того, что система находится в состоянии S2:

3. Найдем вероятность того, что система находится в состоянии S3:

4. Найдем вероятность того, что система находится в состоянии S4:

В результате получаем систему уравнений Колмогорова:

Интегрирование данной системы даст искомые вероятности состояний, как функций времени. Начальные условия берутся в зависимости от того, какого было начальное состояние системы. Если при t=0 система находится в состоянии S1, то начальные условия будут p₁=1, p₂= p₃= p₄=0. Кроме этого, к системе добавляются условия нормировки:

Все уравнения строятся по определенному правилу:

1. В левой части каждого уравнения стоит производная вероятности состояния, а в правой части содержится столько членов, сколько стрелок связано с этим состоянием.

2. Если стрелка направлена «из» состояния, соответствующий член имеет знак “-“, если «в» состояние, то знак “+”.

3.Каждый член равен произведению плотности вероятности перехода (интенсивность), соответствующий данной стрелке, и вероятности того состояния, из которого выходит стрелка.

Пример.

Рассмотрим многоканальную СМО с отказами. Состояние системы характеризуется по числу занятых каналов, т.е. по числу заявок.

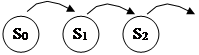
S0 – все каналы свободны

S1 – занят один канал, остальные свободны

Sk – занято k каналов, остальные свободны

Sn – заняты все n каналов.

l

l

l

l

l

l

m

2m

3m

km

(k+1)m

nm

Разметим граф, т.е. проставим у стрелок интенсивности соответствующих потоков событий. Пусть система находится в состоянии S1. Как только закончится обслуживание заявки, занимающей этот канал, система переходит в состояние S0, интенсивность перехода m. Если занято 2 канала, а не один, то интенсивность перехода составит 2m.

Предельные вероятности состояний p₀ и p_n характеризую установившийся режим работы системы массового обслуживания при t® ¥.

— среднее число заявок, приходящих в систему за среднее время обслуживания одной заявки.

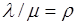
Зная все вероятности состояний p₀ , … , p_{n ,} можно найти характеристики СМО:

· вероятность отказа – вероятность того, что все n каналов заняты

· относительная пропускная способность – вероятность того, что заявка будет принята к обслуживанию

· среднее число заявок, обслуженных в единицу времени

Полученные соотношения могут рассматриваться как базисная модель оценки характеристик производительности системы. Входящий в эту модель параметр l = 1 / t_{ОБРАБОТКИ}, является усредненной характеристикой пользователя. Параметр m является функцией технических характеристик компьютера и решаемых задач.

Эта связь может быть установлена с помощью соотношений, называемых интерфейсной моделью. Если время ввода/вывода информации по каждой задачи мало по сравнению со временем решения задачи, то логично принять, что время решения равно 1 / m и равно отношению среднего числа операций, выполненных процессором при решении одной задачи к среднему быстродействию процессора.

На практике далеко не все случайные процессы являются Марковскими или близкими к ним. В СМО поток заявок не всегда Пуассоновский, ещё реже наблюдается показательное или близкое к нему распределение времени обслуживания.

Для произвольных потоков сообщений, переводящих систему из одного состояния в другое, аналитическое решение получено только для отдельных частных случаев. Когда построение аналитической модели по той или иной причине трудно осуществимо, применяется другой метод моделирования – метод статистических испытаний (Монте-Карло). Широкое распространение метода связано с возможностью его реализации на компьютере.

Идея метода: вместо того, чтобы описывать случайное явление с помощью аналитической зависимости производится «розыгрыш», т.е. происходит моделирование случайного явления с помощью некоторой процедуры, дающей случайный результат. Произведя такой розыгрыш n раз, получаем статистический материал, т.е. множество реализаций случайного явления, которое потом можно обработать обычными методами математической статистики. Метод Монте-Карло предложил Фон-Нейман в 1948 году, как метод численного решения некоторых математических задач.

Суть метода:

1. Вводим в некотором единичном квадрате любую поверхность S.

2. Любым получаем 2 числа x_i, y_i, подчиняющиеся равномерному закону распределения случайной величины на интервале [0, 1].

3. Полагаем, что одно число определяет координату x, второе – координату y

4. Анализируем принадлежность точки (x, y) фигуре. Если принадлежит, то увеличиваем значение счетчика на 1.

5. Повторяем n раз процедуру генерации 2х случайных чисел с заданным законом распределения и проверку принадлежности точки поверхности S.

6. Определяем площадь фигуры как количество попавших точек, к количеству сгенерированных.

Фон-Нейман доказал, что погрешность .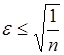

Преимущества метода статистических испытаний в его универсальности, обуславливающей возможность всестороннего статистического исследования объекта, однако, для реализации этой возможности нужны довольно полные статистические сведения о параметрах элементов.

К недостаткам относится большой объем требуемых вычислений, равный количеству обращений к модели. Поэтому вопрос выбора величины n имеет важнейшее значение. Уменьшая n – повышаем экономичность расчетов, но одновременно ухудшаем их точность.

Источник