Способ решения циклических алгоритмов

Способ решения циклических алгоритмов

Циклический алгоритм – описание действий, которые должны повторяться указанное число раз или пока не выполнено заданное условие. Перечень повторяющихся действий называют телом цикла.

Циклические алгоритмы бывают двух типов:
Циклы со счетчиком, в которых какие-то действия выполняются определенное число раз;
Циклы с условием, в которых тело цикла выполняется, в зависимости от какого-либо условия.

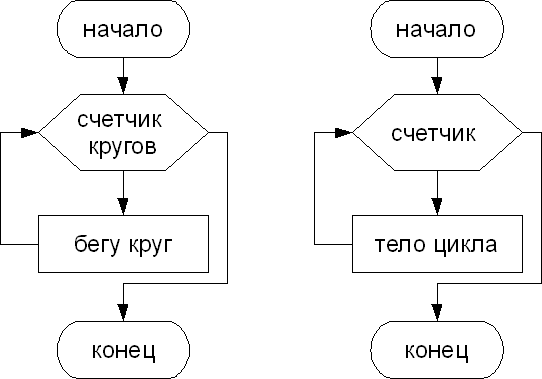
В общем случае схема циклического алгоритма со счетчиком будет выглядеть так:

Для счетчика от нач. значения до кон. значения выполнить действие. Часто бывает так, что необходимо повторить тело цикла, но заранее не известно, какое количество раз это надо сделать. В таких случаях количество повторений зависит от некоторого условия. Такие циклы называются циклы с условием. Циклы в которых сначала проверяется условие, а затем, возможно, выполняется тело цикла называют циклы с предусловием. Если условие проверяется после первого выполнения тела цикла, то циклы называются циклы с постусловием.

Например, в субботу вечером вы смотрите телевизор. Время от времени поглядываете на часы и если время меньше полуночи, то продолжаете смотреть телевизор, если это не так, то вы прекращаете просмотр телепередач.

В общем случае схема циклического алгоритма с условием будет выглядеть так:

Пока условие повторять действие. При составлении циклических алгоритмов важно думать о том, чтобы цикл был конечным. Ситуация, при которой выполнение цикла никогда не заканчивается, называется зацикливанием .

Источник

Способ решения циклических алгоритмов

называется конечной суммой

Для некоторых последовательностей известны формулы расчета конечных сумм, например: при a_n = a_n-1 + d; S_n = (a₁ + a_n)*n/2; — арифметическая прогрессия, при a_n = a_n-1 * q; S_n= (a₁ — a_n*q)/(1-q); — геометрическая прогрессия, где d и q — постоянные числа. Здесь N-ый член последовательности выражается через (N-1)-ый член. Такие зависимости называются реккурентными. Конечная сумма последовательности может быть неизвестна, тогда для ее расчета применяется алгоритм суммирования членов последовательности в цикле от 1 до N. Приведем пример расчета конечной суммы последовательности: 12 + 32 + 52 +. . . + (2*N-1)₂; S_n = N*(4*N₂-1)/3; В некоторых случаях «N»-ый член последовательности определяется через сумму предыдущих членов, например,

и конечную сумму можно рассчитать по формуле:

где «S₀» — начальная сумма. Рассмотрим программу вычисления конечной суммы денежного вклада в банк через N месяцев при ежемесячной процентной ставке «pr» (5% cоответствует pr=5). Часто применяются вложенные операторы цикла. Например, если необходимо провести все варианты расчета при изменении нескольких параметров в заданных диапазонах. Составим программу расчета функции y = A*sin(x) — cos(x)/A; при изменении аргумента «x» в диапазоне от 0 до Pi с шагом Pi/100 и при изменении параметра «A» в диапазоне от 1 до 3 с шагом 0.5.

Операторы цикла с условием

Схема выполнения операторов имеет вид:

Цикл WHILE	Цикл REPEAT

В цикле While «оператор» выполняется если условие верно (True), если условие ложно (False), то цикл заканчивается, т. е. цикл While повторяется пока выполняется условие. Цикл While начинается проверкой условия, поэтому, если начальное условие ложно, то «оператор» не выполняется ни разу. Для включения в тело цикла нескольких операторов применяется составной оператор: Begin «операторы» end. Цикл Repeat повторяется, если условие ложно (False), и заканчивается, если условие верно (True), т. е. цикл Repeat повторяется до выполнения условия. Цикл Repeat заканчивается проверкой условия, поэтому «операторы» выполняются не менее одного раза. В теле цикла может записываться более одного оператора. Циклы с условием обычно используются в тех случаях, если количество повторений блока операторов заранее не известно, например, при расчете суммы членов бесконечного ряда с заданной погрешностью. Сумма членов бесконечной последовательности

называется бесконечным рядом и записывается в виде:

Здесь a_n — общий член ряда. Сумма конечного числа членов ряда называется частичной суммой и обозначается «S_n«. Если сумма членов бесконечного ряда имеет конечный предел «S», то ряд называется сходящимся. Для некоторых рядов получены формулы расчета суммы членов ряда. Например, сумма членов числового ряда:

1 + 1/32 + 1/52 + . . . + 1/(2*N-1) + .

имеет предел S = Pi 2 /8 и общий член a_n = images/(2*N-1) 2 , где N = 1, 2, 3, . Для сходящегося ряда вычисляется последовательность частичных сумм с заданной погрешностью. Абсолютная погрешность расчетов определяется по формуле Eps=abs(S-S_n), либо Eps=abs(a_n), если значение S неизвестно. Относительная погрешность расчетов определяется по формуле Eps_o=abs((S-S_n)/S), либо Eps_o=abs(a_n/S_n). Частичные суммы вычисляются по формуле: S_n = S_n-1 + a_n Для знакопеременного ряда следует добавить k1=-1, а в цикле: k1:=-k1, a_n=k1*a_n. В некоторых случаях «N»-ый член ряда выражается через «N-1»-ый, например, для ряда:

1 + 1/2! + 1/4! + 1/6! + . + 1/(2*N)! + . ; N = 0, 1, 2, .

общий член ряда вычисляется по формуле: a_n = a_n-1*k; Параметр k = a_n/a_n-1 — коэффициент роста вычисляется предварительно (до написания программы). Для данного ряда

Здесь N! = 1*2*3*. *N; — вычисление факториала числа «N», причем 0! = 1. Расчет частичных сумм производится в цикле с условием, например, для данного ряда операторами:

Операторы ограничения и прерывания цикла

Примеры

Пример1: На промежутке от 1 до M найти все числа Армстронга. Натуральное число из n цифр называется числом Армстронга, если сумма его цифр, возведенных в n-ю степень, равна самому числу.

Этапы решения задачи:

1. Математическая модель: xО[1;M], x=
2. Составим блок схему программы:

Распишем составные части блока»Находим все числа Армстронга на заданном промежутке и печатаем их»
Опишем блок «Подсчитываем сколько цифр в числе i»
Опишем блок «Проверяем, является ли i числом Армстронга»
Дальнейшая детализация не требуется, запишем блок-схему целиком:
Дальнейшей детализации не требуется, переведем программу на язык Паскаль.

Контрольные вопросы

1. Как записывается и как работает оператор FOR?
2. Для организации каких циклов применим оператор FOR?
3. В чем отличие оператора WHILE от оператора REPEAT?
4. Как программируются циклические алгоритмы с явно заданным числом повторений цикла?
5. Как программируются циклические алгоритмы с заранее неизвестным числом повторений цикла?
6. Напишите оператор цикла, который не выполняется ни разу.
7. Напишите оператор цикла, который выполняется неограниченное число раз.
8. Замените оператор «Repeat A Until B» равносильным фрагментом программы с оператором While.

Задачи

1. Найти все двузначные числа, сумма цифр которых не меняется при умножении числа на 2,3,4,5,6,7,8,9.
2. Найти все трехзначные числа, сумма цифр которых равна данному целому числу.
3. Найти все трехзначные числа, средняя цифра которых равна сумме первой и третьей цифр.
4. Найти все трехзначные числа, которые можно представить разностью между квадратом числа, образованного первыми двумя цифрами и квадратом третьей цифры.
5. Найти все двузначные числа, сумма квадратов цифр которых делится на 17.
6. Найти все трехзначные числа, представимые в виде сумм факториалов своих цифр.
7. Найти двузначное число, обладающее тем свойством, что куб суммы его цифр равен квадрату самого числа.
8. Найти двузначное число, равное утроенному произведению его цифр.
9. В каких двузначных числах удвоенная сумма цифр равна их произведению?
10. Можно ли заданное натуральное число М представить в виде суммы квадратов двух натуральных чисел? Написать программу решения этой задачи.
    Вычисление выражений:
    Дано натуральное n. Вычислить:
11. ;
12. ;

Дано действительное число х, натуральное число n. Вычислить:

x ( x — n )( x — 2 n )( x — 3 n )…( x — n2 );

;

;
Дано натуральное n. Вычиcлить:

;

;

Вычислить приближенно значение бесконечной суммы (справа от каждой суммы дается ее точное значение, с которым можно сравнить полученный ответ):

= ;

= ;

= ;

Нужное приближение считается полученным, если вычислена сумма нескольких первых слагаемых, и очередное слагаемое оказалось по модулю меньше данного положительного числа e.

Даны два целых числа A и B (A 0). Вывести A в степени N: AN = A·A·. ·A (числа A перемножаются N раз).

Дано вещественное число A и целое число N (> 0). Вывести все целые степени числа A от 1 до N.

Дано вещественное число A и целое число N (> 0). Вывести 1 + A + A2 + A3 + . + AN.

Дано вещественное число A и целое число N (> 0). Вывести 1 — A + A2 — A3 + . + (-1)NAN.

Дано целое число N (> 1). Вывести наименьшее целое K, при котором выполняется неравенство 3K > N, и само значение 3K.

Дано целое число N (> 1). Вывести наибольшее целое K, при котором выполняется неравенство 3K 1). Вывести наименьшее из целых чисел N, для которых сумма 1 + 1/2 + . + 1/N будет больше A, и саму эту сумму.

Дано вещественное число A (> 1). Вывести наибольшее из целых чисел N, для которых сумма 1 + 1/2 + . + 1/N будет меньше A, и саму эту сумму.

Дано целое число N (> 0). Вывести произведение 1·2·. ·N. Чтобы избежать целочисленного переполнения, вычислять это произведение с помощью вещественной переменной и выводить его как вещественное число.

Дано целое число N (> 0). Если N — нечетное, то вывести произведение 1·3·. ·N; если N — четное, то вывести произведение 2·4·. ·N. Чтобы избежать целочисленного переполнения, вычислять это произведение с помощью вещественной переменной и выводить его как вещественное число.

Дано целое число N (> 2) и две вещественные точки на числовой оси: A, B (A 2) и две вещественные точки на числовой оси: A, B (A 0). Последовательность чисел AN определяется следующим образом: A1 = 2, AN = 2 + 1/AN-1, N = 2, 3, . Найти первый из номеров K, для которых выполняется условие |AK — AK-1| 0). Последовательность чисел AN определяется следующим образом: A1 = 1, A2 = 2, AN = (AN-2+ AN-1)/2, N = 3, 4, . Найти первый из номеров K, для которых выполняется условие |AK AK-1| Задачи повышенной сложности

1. Определить, является ли заданное число совершенным , т.е. равным сумме всех своих (положительных) делителей, кроме самого этого числа (например, число 6 совершенно: 6=1+2+3).
2. Дано натуральное k. Напечатать k-ю цифру последовательности 1234567891011121314. в которой выписаны подряд все натуральные числа.
3. Дано натуральное k. Напечатать k-ю цифру последовательности 149162536. в которой выписаны подряд квадраты всех натуральных чисел.
4. Дано натуральное k. Напечатать k-ю цифру последовательности 1123581321. в которой выписаны подряд все числа Фибоначчи.

Источник