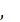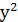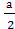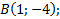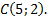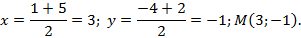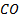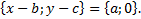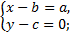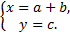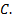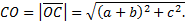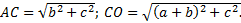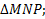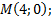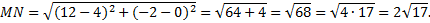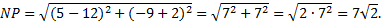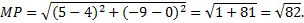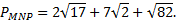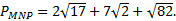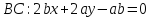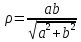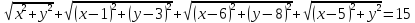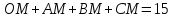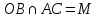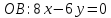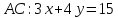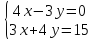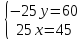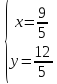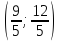Способ решения той или иной задачи есть метод

Статья на тему: «Методы и способы решения текстовых задач»

Методы и способы решения текстовых задач

Начну с того, что же такое задача. Ведь термин задача встречается нам как в быту, так и в профессии. Каждый из нас решает ежедневно те или иные задачи. Задача – это сформулированный словами вопрос, ответ на который может быть получен с помощью арифметических действий. Текстовая задача – описание некоторой ситуации на естественном языке, с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между её компонентами и определить вид этого отношения. Любая текстовая задача состоит из двух частей – условия и требования (вопроса). В условии соблюдаются сведения об объектах и некоторые числовые данные объекта, об известных и неизвестных значениях между ними. Требования задачи – это указание того, что нужно найти. Оно выражено предложением в повелительной или вопросительной форме. Основная особенность текстовых задач состоит в том, что в них не указывается прямо, какое именно действие должно быть выполнено для получения ответа на требование задачи. Ответ на требование задачи получается в результате ее решения. Решить задачу в широком смысле этого слова — это значит раскрыть связи между данными, заданными условием задачи, и искомыми величинами, определить последовательность применения общих положений математики (правил, законов, формул и т. д.), выполнить действия над данными задачи, используя общие положения и получить ответ на требование задачи или доказать невозможность его выполнения.
Прежде всего надо, осознать, что такое текстовая задача. И целью подготовительного периода является возможность показать перевод различных реальных явлений на язык математических символов и знаков. Также для того, чтобы правильно выбрать то или иное действие для решения простой задачи, необходимо сформировать понятие об арифметических действиях, научить выбирать то или иное действие. Решением задачи называют результат, т. е. ответ на требование задачи.

Текстовые задачи мы можем условно классифицировать по типам: задачи на числовые зависимости; задачи, связанные с понятием процента; задачи на «движение», «концентрацию смесей и сплавов», «работу» и т. д.

Решение текстовых задач делится на несколько этапов:

восприятие и осмысление задачи;

поиск плана решения;

выполнение плана решения;

Существуют различные методы решения текстовых задач:

метод проб и ошибок.

В основе каждого метода лежат различные виды математических моделей.

Например, при алгебраическом методе решения задачи составляются уравнения или неравенства, при геометрическом — строятся диаграммы или графики. Решение задачи логическим методом начинается с составления алгоритма.

Следует иметь в виду, что практически каждая задача в рамках выбранного метода допускает решение с помощью различных моделей. Так, используя алгебраический метод, ответ на требование одной и той же задачи можно получить, составив и решив совершенно разные уравнения, используя логический метод — построив разные алгоритмы. Ясно, что в этих случаях мы так же имеем дело с различными методами решения конкретной задачи, которые называю способы решения.

Арифметический метод. Решить задачу арифметическим методом — значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту де задачу во многих случаях можно решить различными арифметическими способами. Задача считается решенной различными способами, если ее решения отличаются связями между данными и искомыми, положенными в основу решений, или последовательностью этих связей.

Алгебраический метод . Решить задачу алгебраическим методом — это значит найти ответ на требование задачи, составив и решив уравнение или системы уравнений (или неравенств). Одну и ту же задачу можно так же решить различными алгебраическими способами. Задача считается решенной различными способами, если для ее решения составлены различные уравнения или системы уравнений (неравенств), в основе составления которых лежат различные соотношения между данными и искомыми.

Геометрический метод. Решить задачу геометрическим методом — значит найти ответ на требование задачи, используя геометрические построения или свойства геометрических фигур.

Логический метод . Решить задачу логическим методом — это значит найти ответ на требование задачи, как правило, не выполняя вычислений, а только используя логические рассуждения.

Практический метод . Решить задачу практическим методом — значит найти ответ на требования задачи, выполнив практические действия с предметами или их копиями (моделями, макетами).

Табличный метод позволяет видеть задачу целиком это — решение путем занесения содержания задачи в соответствующим образом организованную таблицу.

Комбинированный метод позволяет получить ответ на требование задачи более простым путем.

Метод проб и ошибок (самый примитивный), в нем ответ на вопрос задачи угадывается. Но и здесь основные моменты решения — выбор пробных ответов на вопрос задачи и проверка их соответствия условию осуществляется с помощью мыслительных операций, необходимых при решении любым путем. Угадывание ответа требует интуиции, без которой невозможно никакое решение.

Методы решения могут быть разные, но способ решения, лежащий в их основе, может быть один.

Работа над текстовой задачей остается одним из важнейших аспектов обучения в начальной школе, когда закладываются основы знаний; является движущим фактором в развитии младших школьников. Из текстов задач дети открывают новое об окружающем мире, испытывают чувство удовлетворения и радости от их успешного решения.
Решение текстовых задач и нахождение разных способов их решения на уроках математики способствует развитию у детей мышления, памяти, внимания, творческого воображения, наблюдательности, последовательности рассуждения и его доказательности, развитию умения кратко, четко и правильно излагать свои мысли.

При решении любых текстовых задач на движение наиболее рационально принимать в качестве неизвестных величин расстояние, скорость или наименьшую из величин, что приводит к более короткому решению. Если после составления уравнений, полученная система не решается, то необходимо попробовать выбрать другие неизвестные. Количество неизвестных не имеет значения, правильное составление системы превыше всего. Также, нужно обращать особое внимание на единицы измерения – в течение всего решения они обязательно должны быть одинаковыми. А именно, если это часы, то на протяжении всей задачи время должно выражаться в часах, а не в минутах, так и, километры и метры не должны применяться в одном решении и т. п.

Для преобразования условия задачи в математическую модель математические знания практически не нужны – здесь необходим здравый смысл. Очень важно обязательно сформулировать, используя переменные, что мы обязаны найти, т. к. переменных может быть намного больше, чем уравнений, где все их найти просто невозможно.

Решая системы нужно помнить, что в текстовых задачах все величины, как правило, положительны, т. к. в природе отрицательных скоростей и расстояний не существует. Это даёт нам право на умножение, деление и на возведение в квадрат получающиеся уравнения и неравенства.

Решая задачи «на работу», очень выгодно принимать за неизвестные величины производительность (работа, производимая за единицу времени), но бывают и исключения, где необходимо за неизвестную, например, выбрать время. Иногда встречаются такие задачи, в которых не указывается, какая работа выполняется. В таких задачах, будет удобнее ввести самим единицу работы, равную всей работе. Во время исследования была обнаружена всего одна задача, где помимо рассмотрения деятельности всех рабочих, важно рассмотреть их совместную деятельность, а иначе задача будет решена не верно.

В задах «на производительность» стоит лишь отметить то, что за производительность трубы принимается объём жидкости, протекающей через неё за единицу времени. Также, бывают случаи, когда необходимо принять за неизвестные одновременно объём бассейна, производительность труб и время наполнения бассейна каждой трубой, чего не стоит опасаться.

Источник

Способ решения той или иной задачи есть метод

Введение

Федеральные государственные образовательные стандарты выдвигают новые социальные требования не только к результатам реализации основной образовательной программы, но и к системе школьного образования в связи с чем необходимым условием является пересмотр методов и технологий, применяемых для формирования различных универсальных учебных действий обучаемых. Развитие личности обучающегося на основе усвоения универсальных учебных действий, познания и освоения мира составляет цель и основной результат образования. Как проконтролировать результаты обучения? Как зафиксировать продвижение учащегося к планируемым результатам? Понятно, что это прерогатива рабочей программы учителя. Рабочая программа разрабатывается учителем и отражает особенности преподавания математики в конкретном классе конкретного образовательного учреждения. Этот документ — индивидуальный инструмент педагога, с помощью которого учитель определяет оптимальные и наиболее эффективные для получения результата методы и приемы организации образовательного процесса. В геометрии применяются различные методы решения задач — это синтетический (чисто геометрический) метод, метод преобразований, векторный, метод координат и другие. Они занимают различное положение в школе. Основным методом считается синтетический, а из других наиболее высокое положение занимает метод координат потому, что он тесно связан с алгеброй. Изящество синтетического метода достигается с помощью интуиции, догадок, дополнительных построений. Координатный метод этого не требует: решение задач во многом алгоритмизировано, что в большинстве случаев упрощает поиск и само решение задачи. Можно с уверенностью говорить о том, что изучение данного метода является неотъемлемой частью школьного курса геометрии. Но нельзя забывать, что при решении задач координатным методом необходим навык алгебраических вычислений и не нужна высокая степень сообразительности, а это в свою очередь негативно сказывается на творческих способностях учащихся. Поэтому необходима методика изучения метода координат, позволяющая учащимся научиться решать разнообразные задачи координатным методом, однако не показывающая , что этот метод как основной для решения геометрических задач. Также многие геометрические задачи решаются очень сложно, а с применением этого метода, решение упрощается.

Этим и определяется актуальность выбранной темы: «Применение метода координат при решении планиметрических задач»

Объект исследования: решение планиметрических задач

Предмет исследования: метод координат как способ решения геометрических задач

Целью исследования было показать преимущество применения этого метода для решения геометрических задач

Гипотеза исследования. Исходное предположение заключалось в том, использование метода координат для решения некоторых геометрических задач целесообразнее .

В соответствии с целью и выдвинутой гипотезой были поставлены следующие задачи исследования:

Изучить литературу по данной проблеме.

Проверить эффективность метода при решении конкретных геометрических задач.

Практическая значимость исследования. Метод координат в геометрии в том и состоит, что посредством координат точек геометрические объекты задают аналитически с помощью чисел, уравнений, неравенств или их систем и тем самым при доказательстве теорем или решении геометрических задач используют аналитические методы. Это существенно упрощает рассуждение и часто позволяет доказывать теоремы или решать задачи, пользуясь определенным алгоритмом (производя те или иные вычисления), в то время, как синтетический метод в геометрии в большинстве случаев требует искусственных приемов. Овладение универсальными учебными действиями – это требование стандартов образования нового поколения.

В работе будут использоваться эмпирические методы, включающие: наблюдение; экспериментальные методы, анализ продуктов деятельности.

Метод координат

Метод координат — способ определять положение точки или тела с помощью чисел или других символов (например, положение шахматных фигур на доске определяется с помощью чисел и букв). Числа (символы), определяющие положение точки (тела) на прямой, плоскости, в пространстве , на поверхности и так далее, называются её координатами. В зависимости от целей и характера исследования выбирают различные системы координат. Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющий положение конкретной точки, называется координатами этой точки. В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа. В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.

В географии координаты — широта, долгота и высота над известным общим уровнем (например, океана).

В астрономии координаты — величины, при помощи которых определяется положение звезды, например, прямое восхождение и склонение.

Небесные координаты — числа, с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой систему полярных координат на сфере с соответствующим образом выбранным полюсом. Систему небесных координат задают большим кругом небесной сферы (или его полюсом, отстоящим на 90° от любой точки этого круга) с указанием на нём начальной точки отсчёта одной из координат. В зависимости от выбора этого круга системы небесных координат называлась горизонтальной, экваториальной, эклиптической и галактической.

Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае.

Прямоугольная система координат на плоскости

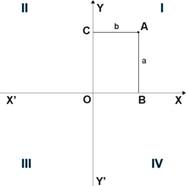
Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси X’X против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y’Y. Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y, называются координатными углами. Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: A(a, b). Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.

Основная заслуга в создании современного метода координат принадлежит французскому философу, математику и естествоиспытателю Рене Декарту (1595-1650) — чьим именем названы прямоугольные координаты. Приходя в театр, мало кто задумывается о происхождении простой вещи: нумерация кресел по рядам и местам. А ведь когда-то это было большой проблемой. До наших времен дошла история: Декарт, посещая парижские театры, постоянно удивлялся, почему же происходит такая путаница и ругань при распределении публики в зрительном зале. Оказывается, ряды и места, попросту, не имели номеров. Тогда-то он и предложил ввести систему нумерации, в которой каждое место получало номер ряда и порядковый номер от края. Эта система используется и в наши дни. Важное место в истории координат занимают работы Рене Декарта: «Рассуждение о методе» (1637г) и «Геометрия» (1637). В первой работе Р. Декарт впервые научно описал прямоугольную систему координат. Именно поэтому прямоугольную систему координат также называют декартовой системой координат. В «Геометрии» Декарт открыл и показал связь алгебры и 8 геометрии. Он впервые ввел понятия переменной величины и функции. Этот научный труд дал огромный толчок в развитии математики. В декартовой системе координат получили реальное истолкование отрицательные числа. Развитие алгебры и геометрии в течение тысячелетий шло независимо друг от друга, между ними была очень слабая связь. Во времена Декарта эти две ветви уже достигли высокой степени развития, но именно с появлением аналитической геометрии появилось новое направление в изучении, устанавливающее тесную связь между геометрией и алгеброй. Любую точку пространства или плоскости можно определять с помощью чисел – ее координат. Это означает, что любую фигуру можно «зашифровать» с помощью чисел. Соотношения между координатами чаще всего определяет не одну точку, а некоторое множество (совокупность) точек. Например, если отметить все точки, у которых абсцисса равна ординате, т. е. 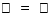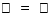точки, координаты которых удовлетворяют уравнению , то получится прямая линия — биссектрисы первого и третьего координатных углов.(рис.1) Рис.1 Иногда понятие «множество точек» заменяют на «геометрическое место точек». Например, геометрическое место точек, координаты которых 9 удовлетворяют соотношению – это и есть биссектрисы первого и третьего координатного угла. Именно открытие связи между алгеброй и геометрией дало толчок для нового направления в развитии математики. Эти знания начали развивать математику как единую науку, в которой все ее части неотделимы друг от друга. Нельзя не сказать о французском математике Пьере Ферма. В его работах сделан большой вклад в развитие координатного метода, они впервые были опубликованы уже после его смерти. Ферма и Декарт изучали применение метода координат только на плоскости, а вот в трехмерном пространстве впервые применил этот метод Леонард Эйлер в 18 веке. Координаты дают возможность наглядно при помощи графика изобразить зависимость одной величины от другой. В современном мире в различных областях данные знания широко используются. Именно поэтому большое количество специалистов разных направлений имеют представление о прямоугольных декартовых координатах на плоскости.

Анализ школьных учебников

В школьном курсе геометрии существуют различные методы для решения задач и доказательства теорем. К ним можно отнести синтетический метод, метод геометрических преобразований, векторный метод и метод координат, которые в свою очередь связаны между собой. Тот или иной метод в школьных учебниках может занимать преобладающее значение. в зависимости от раскрываемой авторами концепции.

Рассмотрев школьную программу по геометрии основной школы, можно сказать, что координатному методу уделяется мало внимания. Раздел программы « Цели изучения курса геометрии» рассматривает: « при решение задач и доказательстве теорем…применяются геометрические преобразования, векторы и координаты». Значит программа не ставит цель – изучить метод координат, как метод решения геометрических задач. В программе говорится, что « в результате изучения курса геометрии учащиеся должны уметь использовать координаты для решения несложных задач

Атанасян Л. С. в учебнике геометрии 7-9классов[1], изучению координатного метода посвятил целую главу. В этой главе в §1 рассматривается координаты вектора и разложение вектора по двум неколлинеарным векторам; во §2 решаются простейшие задачи в координатах, изучается связь между координатами вектора и координатами его начала и конца; и в §3 уравнение прямой и окружности. Координатный метод в данной главе трактуется как метод, изучающий геометрические фигуры средствами алгебры. Главной целью автора является, обучить учащихся применению координатного метода для решения задач на построение фигур, для доказательства задач и вывода геометрических формул.

Так в учебнике Погорелова А. В. геометрия 7-11 классов[7], координатный метод занимает одно из центральных мест. Координаты начинают изучать с восьмого класса, изучив темы «Четырехугольники» и «Теорема Пифагора». Сначала изучают основные понятия, это введение координат на плоскости, уравнения прямой и окружности, после рассматривают пересечение двух окружностей, пересечение прямой и окружности, определяют sin, cos и tg любого угла. Изучение данных тем являются начальным изучением координатного метода в школе.

И наконец, в учебнике Шарыгина И. Ф. геометрия 7-9 классов[7],большое внимание уделяется методам решения геометрических задач, по сравнению с учебниками Атанасяна Л.С. и Погорелова А.В. В данном учебнике координатный метод изучается в конце девятого класса. Изучая эту тему, школьники знакомятся с декартовыми координатами на плоскости, уравнениями прямой и окружности. Нужно отметить, что изучению данной темы уделяется мало теоретического материала. Шарыгин не рассматривает формулу середины отрезка, не дает определения фигуры, зато изучает уравнение «плоских линий», которые необходимы для решения задач. Метод координат начинает рассматривать после изучения векторов. Приводится достаточное количество задач на эту тему. Автор приводит два примера,

вначале рассматривается окружность Аполлония, затем уделяется внимание выбору системы координат. К ним относятся сложные задачи, связанные с нахождением геометрического места точек.

Методические аспекты изучения и применения метода координат в геометрии

Решение задач координатным методом происходит по алгоритму, что в свою очередь, упрощает поиск и само решение задачи. Данный метод переносит в геометрию важную особенность алгебры – единообразие способов для решения той или иной задачи. В отличие от арифметики и элементарной геометрии, в алгебре и аналитической геометрии решение задач приводится по общему для всех задач плану, практически подходящему к любой задаче. Применение координатного метода для решения геометрических задач, избавляет от необходимости наглядного представления сложных пространственных изображений. Сущность метода координат как метода решения задач состоит в том, что, задавая фигуры уравнениями и выражая в координатах различные геометрические соотношения, мы можем решать геометрическую задачу средствами алгебры. Метод координат – это универсальный метод. Он обеспечивает тесную связь между алгеброй и геометрией, которые, соединяясь, дают «богатые плоды», какие они не могли бы дать, оставаясь разделенными.

Суть метода координат

Сущность метода координат как метода решения задач состоит в том, что, задавая фигуры уравнениями и выражая в координатах различные геометрические соотношения, мы можем решать геометрическую задачу средствами алгебры. Метод координат – это универсальный метод. Он обеспечивает тесную связь между алгеброй и геометрией, которые, соединяясь, дают «богатые плоды», какие они не могли бы дать, оставаясь разделенными.В некоторых случаях метод координат дает возможность строить доказательства и решать многие задачи более рационально, красиво, чем чисто геометрическими способами. В отношении школьного курса геометрии можно сказать, метод координат связан, правда, с одной геометрической сложностью. Одна и та же задача получает различное аналитическое представление в зависимости от того или иного выбора системы координат. И только достаточный опыт позволяет выбирать систему координат наиболее целесообразно.

Алгоритм решения задач методом координат

С помощью метода координат, можно решать задачи двух видов.

1.Пользуясь координатами можно истолковать уравнения и неравенства геометрически и таким образом применять геометрию к алгебре и анализу. Графическое изображение функции первый пример такого применения координатного метода.

2.Задавая фигуры уравнениями и выражая в координатах геометрические соотношения, мы применяем алгебру к геометрии. Например, можно выразить через координаты основную геометрическую величину — расстояние между точками.

Решение задач, как алгебраических, так и геометрических методом координат сводится к выполнению определенного алгоритма, состоящего из следующие шагов.

Перевести задачу на координатный (аналитический) язык.

Выполнить преобразование аналитического выражения.

Сделать обратный перевод, т. е. перевод с координатного языка на язык, в терминах которого сформулирована задача.

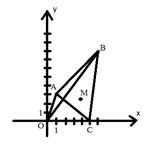
Задача. 1.В треугольнике ABC: AC=b, AB=c, ВС=а, BD — медиана. Докажите, что .

Первый шаг. Выберем систему координат так, чтобы точка А служила началом координат, а осью Ох — прямая АС (рис.).

Важно оптимально выбирать систему координат, т. е. так, чтобы наиболее просто находить координаты данных точек.

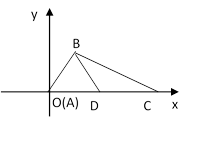
В выбранной системе координат точки А, С и D имеют следующие координаты: А(0,0), D(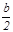,0) и С(b,0).

Обозначим координаты точки В через х и у. Тогда используя формулу для нахождения расстояний между двумя точками, заданными своими координатами, получаем:

(1)

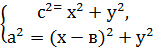
По той же формуле 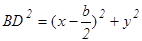. (2)

Решив систему уравнений (1), найдем х и у:

; .

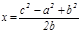
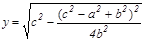
Подставляя результат в формулу (2), получаем: .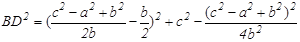

.

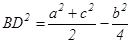
Задача №2. Даны две точки. Найдите множество точек, для каждой из которых расстояния от двух данных точек равны.

Первый шаг. Обозначим точки через A и B. Введем прямоугольную систему координат с началом в точка A. ( формируется умение оптимального выбора системы координат). Отсюда следует, что AB=а, тогда в данной системе точки имеют следующие координаты А(0,0) и В(а,0). Обозначим произвольную точку так, чтобы выполнялось условие AM=MB (АМ2=МВ2).Точка М имеет координаты М(х,у). Используем формулу расстояния от одной точки до другой, получаем

=+

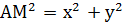
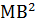
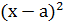
Тогда 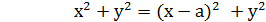уравнение окружности.

Второй шаг. Осуществим преобразование данного выражения, в результате получим соотношение: х =

Третий шаг. Выполним обратный перевод с языка уравнения на геометрический язык. Данное уравнение – это уравнение прямой, параллельной оси Оу и стоящей от точки А на расстояние d=, то есть серединного перпендикуляра к отрезку AB.

Разновидности задач, обучающие методу координат

Разрабатывая методику формирования умений применения метода координат, важно выявить требования, предъявляющая логическая структура решения задач к мышлению учащихся. Метод координат предусматривает наличие у учащихся навыков и умений, которые способствуют применению координатного метода на практике. Проведем анализ решения задач данным методом для выявления компонентов умения использовать метод координат. Благодаря чему, осуществиться поэлементное формирование умений использования координатного метода решения задач.

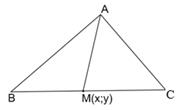
Дан треугольник с вершинами 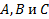. Найти медиану: АМ .

Дано:

;

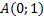
Найти: .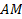

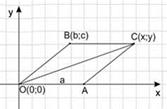
Решение: Найдем координаты точки 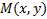как середины отрезка ВС:

Найдем длину отрезка :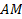

.

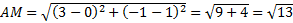
Ответ: .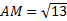

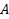
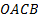
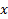
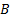
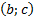
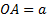
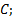
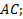
Задача 2.Вершина параллелограмма лежит на положительной полуоси , вершина имеет координаты ; . Найти координаты точки сторону диагональ

Решение: Построим данный параллелограмм в прямоугольной системе координат

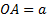
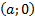
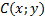
Так как , то координаты точки . Пусть координаты точки .

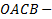
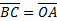
Так как параллелограмм, то ;

Координаты равны, следовательно,

Итак, ;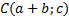

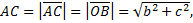
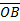
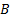
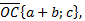
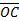
так как вектор имеет те же координаты, что и точка .

так как координаты вектора совпадают с координатами точки

Ответ: ;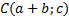

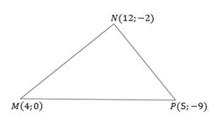
Задача 3.Найти периметр треугольника, если известны координаты его вершин

Дано:

;

.

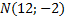
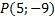
Найти: периметр .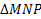

Воспользуемся формулой вычисления расстояния между точками.

Найдем длину :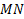

Найдем длину :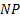

Найдем длину :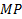

Ответ:

Несмотря на то что метод координат имеет некоторые недостатки, такие как наличие большого количества дополнительных формул, необходимых запомнить, и отсутствие предпосылок развития творческих способностей учащихся, некоторые виды задач трудно решить без применения данного метода. Поэтому изучение координатного метода необходимо, нужно детальное знакомство с этим методом .

Задача №4. Найти расстояние между центрами вписанной и описанной окружностей прямоугольного треугольника с катетами 3 см и 4 см. Для решения этой задачи целесообразно применить координатный метод и метод геометрических мест. Решение. Пусть АВС — данный треугольник. LС=90°, АС=4, ВС=3. Поместим его в систему координат: С=0, АС=0Y, BC=0X. Тогда С(0;0), А(0;4), В(0:3). Пусть К центр описанной окружности, тогда К- середина АВ и К(1,5;2). Пусть М — центр вписанной окружности. Координаты точки М равны, так как она принадлежит биссектрисе угла С и каждая из них равна радиусу вписанной окружности. Стороны треугольника составляют 3, 4, 5, тогда r=3+4−5 2 =1, то есть М(1;1). 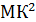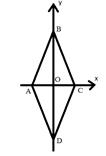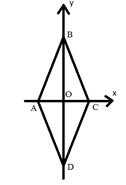По формуле расстояния между двумя точками найдем расстояние между центрами окружностей: =(1,5 − 1)2 + (2 − 1)2 МК=√1,25=√5 2 . Ответ: √5 2

Вычислите расстояние между прямыми, содержащими противоположные стороны ромба, если длины его диагоналей равны .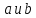

Решение

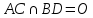
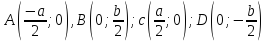
Введем прямоугольную декартову систему координат. Пусть ABCD – ромб. . Точка О – начало координат. Вершины ромба имеют координаты:

.

Расстояние от точки А до прямой ВС равно:

.

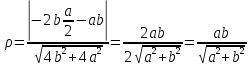
Ответ:

Решение

Введем прямоугольную декартову систему координат. Пусть .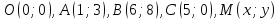

Ответ:

Заключение

Достаточно простой в применении, метод координат является необходимой составляющей решения задач различного уровня. Использование данного метода, позволяет учащимся значительно упростить и сократить процесс решения задач, что помогает им при дальнейшем изучении, как школьного курса математики, так и при изучении математики в высших учебных заведениях.

В данной работе:

1)проанализировано несколько действующих школьных учебников относительно темы «Метод координат»;

2)описан сам метод координат, виды и этапы решения задач методом координат;

3) выделены основные умения, необходимые для овладения данным методом и приведен ряд задач, формирующих их.

4) разработан конспект урока с технологической картой

Также выдвинутая гипотеза о том, что изучение метода координат в школьном курсе геометрии необходимо. Оно будет более эффективно, если в 5-6 классе проведена пропедевтическая работа по формированию основных умений и навыков, в системном курсе планиметрии учащиеся знакомятся со структурой данного метода, и используется продуманная система задач для формирования отдельных компонентов метода.

Источник