Способ решения квадратных уравнений по теореме безу

Содержание

Об уравнениях высших степеней
Кубические уравнения
Возвратные кубические уравнения
Теорема Безу и схема Горнера
Возвратные биквадратные уравнения
Область применения
Разложение многочлена на множители. Часть 3. Теорема Безу и схема Горнера

Об уравнениях высших степеней

Как правило в физике, информатике и экономике мы сталкиваемся с простейшими линейными, или дробно-рациональными уравнениями, реже с квадратными. А что до уравнений третьей и четвёртой степени? Если вам интересно, то прошу под кат.

Для начала рассмотрим понятие уравнения высшей степени. Уравнением высшей степени, называется уравнение вида:

В этой статье я рассмотрю:

1. Кубические уравнения.
2. Возвратные кубические.
3. Применение схемы Горнера и теоремы Безу.
4. Возвратные биквадратные уравнения.

Кубические уравнения

Кубические уравнения, это уравнения, в которых у неизвестной при старшем члене степень равна 3. Кубические уравнения имеют следующий вид:

Решать такие уравнения можно по разному, однако мы воспользуемся знаниями базовой школы, и решим кубическое уравнение методом группировки:

В данном примере используется метод группировки, группируем первые два и последние два члена, получая равные скобки, снова выносим, получая уравнение из двух скобок.

Произведение равно нулю тогда, и только тогда, если хотя бы один из множителей равен нулю, на основании этого мы каждый множитель (скобку) приравниваем к нулю, получая неполное квадратное и линейное уравнения.

Также стоит отметить, что максимальное количество корней уравнения, равно степени неизвестной при главном члене, так в кубическом уравнении может быть не более трёх корней, в биквадратном (4-ой степени) не более четырёх корней и. т. д.

Возвратные кубические уравнения

Возвратные кубические уравнения имеют вид:

Возвратными они называются потому что коэффициенты будут зеркально повторяться. Подобные уравнения тоже решаются школьными методами, но чуть хитрее:

Сначала производится группировка, потом при помощи формул сокращённого умножения мы раскладываем получаемое на множители. Снова получаем 2 равные скобки, «выносим их». Получаем два множителя (скобки) и решаем их как два различных уравнения.

Теорема Безу и схема Горнера

Теорема Безу была открыта, как ни удивительно, Этьеном Безу, французским математиком, занимавшимся в основном алгеброй. Теорему Безу, можно сформулировать следующим образом:

Давайте разберёмся. P(x) — это какой-либо многочлен от x, (x — a) — это двучлен в котором a — это один из целых корней уравнения, который мы находим среди делителей свободного члена.

Три точки, это оператор обозначающий что одно выражение делится на другое. Из этого следует что найдя хотя бы один корень данного уравнения, мы сможем применить к нему эту теорему. Но зачем нужна эта теорема, каково её действие? Теорема Безу — это универсальный инструмент, если вы хотите понизить степень многочлена. Например, при её помощи, кубическое уравнение, можно превратить в квадратное, биквадратное, в кубическое и т. д.

Но одно дело понять, а как поделить? Можно конечно, делить и в столбик, однако этот метод доступен далеко не всем, да и вероятность ошибиться очень высока. Поэтому есть и иной путь, это схема Горнера. Её работу я поясню на примере. Предположим:

И так, нам дан многочлен, и мы возможно заранее нашли один из корней. Теперь мы рисуем небольшую табличку из 6 столбцов и 2 строк, в каждый столбец первой строки (кроме первого), мы вносим коэффициенты уравнения. А в первый столбец 2 строки мы вносим значение a (найденный корень). Потом первый коэффициент, в нашем случае 5, мы просто сносим вниз. Значения последующих столбиков мы рассчитываем так:

(Картинка позаимствована здесь)
Далее поступаем точно так же и с остальными столбцами. Значение последнего столбца (2 строки) будет остатком от деления, в нашем случае 0, если получается число отличное от 0, значит надо избрать другой подход. Пример для кубического уравнения:

Возвратные биквадратные уравнения

Выше мы так же рассматривали возвратные кубические уравнения, а теперь разберём биквадратные. Их общий вид:

В отличие от кубического возвратного уравнения, в биквадратном пары, относительно коэффициентов, есть не у всех, однако в остальном они очень схожи. Вот алгоритм решения таких уравнений:

Как видно, решать такие уравнения совсем не просто. Но я всё равно разберу и этот случай. Начинается решение с деления всего уравнения на x^2. Далее мы группируем, здесь я специально ввёл дополнительную строку для ясности. После этого мы совершаем хитрость, и вводим в первую скобку 2, которую мы сначала прибавляем, а после вычитаем, сумма всё равно не изменится, зато теперь мы можем свернуть эту скобку в квадрат суммы.

Уберём -2 из скобки, предварительно домножив его на a, после чего вводим новую переменную, t и получаем квадратное уравнение.

А теперь перейдём к примеру:

Основная часть так же как и в обобщённом алгоритме, делим на x^2, группируем, сворачиваем в полный квадрат, выполняем подстановку переменной и решаем квадратное уравнение. После этого полученные корни подставляем обратно, и решаем ещё 2 квадратных уравнения (с умножением на x).

Область применения

В виду своей громоздкости и специфичности уравнения высших степеней редко находят себе применение. Однако примеры всё же есть, уравнение Пуассона для адиабатических процессов в Физике.

Источник

Разложение многочлена на множители. Часть 3. Теорема Безу и схема Горнера

Разложение многочлена на множители. Теорема Безу и схема Горнера

При решении уравнений и неравенств нередко возникает необходимость разложить на множители многочлен, степень которого равна трем или выше. В этой статье мы рассмотрим, каким образом это сделать проще всего.

Как обычно, обратимся за помощью к теории.

Теорема Безу утверждает, что остаток от деления многочлена на двучлен равен .

Но для нас важна не сама теорема, а следствие из нее:

Если число 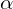является корнем многочлена , то многочлен делится без остатка на двучлен .

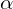
Перед нами стоит задача каким-то способом найти хотя бы один корень многочлена, потом разделить многочлен на , где — корень многочлена. В результате мы получаем многочлен, степень которого на единицу меньше, чем степень исходного. А потом при необходимости можно повторить процесс.

Эта задача распадается на две: как найти корень многочлена , и как разделить многочлен на двучлен.

Остановимся подробнее на этих моментах.

1. Как найти корень многочлена.

Сначала проверяем, являются ли числа 1 и -1 корнями многочлена.

Здесь нам помогут такие факты:

Если сумма всех коэффициентов многочлена равна нулю, то число является корнем многочлена.

Например, в многочлене сумма коэффициентов равна нулю: . Легко проверить, что является корнем многочлена.

Если сумма коэффициентов многочлена при четных степенях 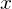равна сумме коэффициентов при нечетных степенях, то число является корнем многочлена. Свободный член считается коэффициентом при четной степени, поскольку , а — четное число.

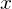
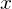
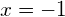
Например, в многочлене сумма коэффициентов при четных степенях : , и сумма коэффициентов при нечетных степенях : . Легко проверить, что является корнем многочлена.

Если ни 1, ни -1 не являются корнями многочлена, то двигаемся дальше.

Для приведенного многочлена степени 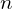(то есть многочлена, в котором старший коэффициент — коэффициент при — равен единице) справедлива формула Виета:

, где — корни многочлена .

Если многочлен не является приведенным, то его можно сделать таковым, разделив на старший коэффициент.

Есть ещё 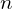формул Виета, касающихся остальных коэффициентов многочлена, но нас интересует именно эта.

Из этой формулы Виета следует, что если корни приведенного многочлена целочисленные, то они являются делителями его свободного члена, который также является целым числом.

Исходя из этого, нам надо разложить свободный член многочлена на множители, и последовательно, от меньшего к большему, проверять, какой из множителей является корнем многочлена.

Рассмотрим, например, многочлен .