Главная » Разное

Способ решения кронекера капелли

Содержание
  1. Теорема Кронекера-Капелли
  2. ЕГЭ2022 (математика профиль) в ВК Скоро вебинар «ПРЯМАЯ НА ПЛОСКОСТИ» (Аналитическая геометрия). Жми подробнее. Теорема Кронекера-Капелли. Метод Гаусса. «Если Вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.» Д. Пойа (1887-1985 г.) (Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.) Пусть дана система m линейных уравнений с n неизвестными . На вопрос о совместности этой системы дает теорема Кронекера-Капелли. Какая система называется совместной читать здесь Теорема Кронекера-Капелли: Система линейных уравнений (СЛУ) совместна тогда и только тогда, когда ранг расширенной матрицы системы (rp) равен рангу основной матрицы (ro). Что называется расширенной матрицей читать здесь Что такое ранг матрицы и как его найти читать здесь Правила отыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем. Теорема 1: Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Теорема 2: Если ранг совместной системы меньше числа неизвестных, то система имеет бесконечно много решений. МЕТОД ГАУССА Одним из наиболее универсальных и эффективных методов решения СЛУ является МЕТОД ГАУССА, состоящий в последовательном исключении неизвестных. СУЩНОСТЬ МЕТОДА ГАУССА. Расширенную матрицу системы с помощью элементарных преобразований приводят к ступенчатой, восстанавливают систему, которая является равносильной исходной системе, и находят решение. Как данную матрицу привести к ступенчатой читать здесь Рассмотрим этот метод на примерах. ПРИМЕР 1: РЕШЕНИЕ: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду. Ранг основной матрицы равен 2 (ro=2), а ранг расширенной – 3 (rp=3), поэтому по теореме Кронекера-Капелли система несовместна. (Последняя строка представляет собой уравнение вида: 0=1. Поэтому делаем вывод, что система несовместна.) Ответ: система несовместна. Замечание: Если хотя бы одна строка имеет вид: то система несовместна. ПРИМЕР 2: ro=rp=3, поэтому по теореме Кронекера-Капелли система совместна, причем ранг системы равен числу неизвестных, следовательно система имеет единственное решение. Ответ: (4;1;-5) ПРИМЕР 3: РЕШЕНИЕ: Третья и четвертая строки получились нулевыми. Их можно вычеркнуть. ro=rp=2, поэтому по теореме Кронекера-Капелли система совместна, причем ранг системы меньше числа неизвестных, следовательно система имеет бесконечное число решений. Ответ: В открывшемся окне: поставить галочку возле «Добавить сообщение получателю» в появившемся поле оставить сообщение «в дар» или «подарок». ИЛИ
    3. оставить комментарий ниже.
Упражнения к уроку: Решите системы методом Гаусса ; 3.Система несовместна. Автор: Аникина Анна Комментарии к этой заметке: Добавить Ваш комментарий Хотите внести свою лепту в его развитие!? Тогда Вам сюда! Источник учимся программировать Программированию нельзя научить, можно только научится Главная » Уроки по Численным методам » Урок 14. Решение систем линейных уравнений (СЛУ). Теорема Кронекера-Капелли. Решение СЛУ с помощью матричных уравнений Урок 14. Решение систем линейных уравнений (СЛУ). Теорема Кронекера-Капелли. Решение СЛУ с помощью матричных уравнений Система линейных уравнений: (1) Здесь и (i =1..m, j=1..n) — заданные, а — неизвестные действительные числа. Матричной записью системы линейных уравнений называется выражение вида: =, или кратко: = (2), где: = = = столбец свободных членов Упорядоченная совокупность n вещественных чисел (c1, c2. cn) называется решением системы(1), если в результате подстановки этих чисел вместо соответствующих переменных x1, x2. xn каждое уравнение системы обратится в арифметическое тождество; другими словами, если существует вектор C= (c1, c2. cn)T такой, что AC = B. СЛУ называется совместной, или разрешимой, если она имеет, по крайней мере, одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений. Матрица , образованная путем приписывания справа к матрице A столбца свободных членов, называется расширенной матрицей системы. Вопрос о совместности системы (1) решается следующей теоремой. Теорема Кронекера-Капелли Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. Система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение. Пример. Исследовать систему линейных уравнений Решение. Составим расширенную матрицу системы и с помощью элементарных преобразований вычислим одновременно ранги обеих матриц. Далее умножим вторую строку на -2 и сложим с третьей, а затем сложим третью строку с последней. Имеем . Ранг матрицы системы =3, так как матрица имеет три ненулевых строки, а ранг расширенной матрицы =4. Тогда согласно теореме Кронекера-Капелли система не имеет решений. Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, — так называемые системы крамеровского типа: a11 x1 + a12 x2 +. + a1n xn = b1, a21 x1 + a22 x2 +. + a2n xn = b2, (3) . . . . . . an1 x1 + an1 x2 +. + ann xn = bn. Системы (3) решаются одним из следующих способов: 1) методом Гаусса, или методом исключения неизвестных; 2) по формулам Крамера; 3) матричным методом. Матричный метод Если матрица А системы линейных уравнений невырожденная, т.е. det A=0, то матрица А имеет обратную, и решение системы (3) совпадает с вектором . Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X=C, C=A-1B называют матричным способом решения системы, или решением по методу обратной матрицы. Задание 1: Решить систему уравнений матричным способом в Excel Ход решения: Сначала надо записать систему в матричном виде и ввести ее на лист Excel: , здесь , Затем надо с помощью Excel найти обратную матрицу для матрицы А. Далее полученную матрицу нужно умножить на матрицу В. В результате получим ответ: Задание 2: Самостоятельно решить матричным способом систему уравнений Ответ для самопроверки: Источник
  • Упражнения к уроку:
  • учимся программировать
  • Программированию нельзя научить, можно только научится
  • Урок 14. Решение систем линейных уравнений (СЛУ). Теорема Кронекера-Капелли. Решение СЛУ с помощью матричных уравнений
  • Система линейных уравнений:
  • Теорема Кронекера-Капелли
  • Матричный метод
  • Задание 1: Решить систему уравнений матричным способом в Excel
  • Задание 2: Самостоятельно решить матричным способом систему уравнений
    • Читайте также:  Способ переживания бактериями неблагоприятных условий

    Теорема Кронекера-Капелли

    Совместная система линейных уравнений имеет единственное решение, если ранг этой системы равен количеству переменных.

    Совместная система линейных уравнений имеет бесконечное множество решений, если ранг этой системы меньше количества переменных.

    Пример №1 . Исследовать систему алгебраических уравнений (без непосредственного решения системы) с помощью теоремы Кронекера-Капелли.
    Запишем систему в виде:

    Для удобства вычислений поменяем строки местами:

    Добавим 2-ую строку к 1-ой:

    Добавим 3-ую строку к 2-ой:

    Умножим 3-ую строку на (2). Добавим 4-ую строку к 3-ой:

    Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:

    Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:

    Добавим 2-ую строку к 1-ой:

    Это соответствует системе:
    -3x2 + 9x3 = 6
    -4x1 + 5x2 + 7x3 — 10x4 = 0
    За базисные переменные примем x1 и x2. Тогда свободные x3,x4.
    Ранг основной матрицы равен 2. Ранг расширенной матрицы тоже равен 2. Система совместна и имеет бесконечное множество решений.

    Пример №2 .
    Запишем систему в виде:

    Для удобства вычислений поменяем строки местами:

    Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:

    Умножим 2-ую строку на (2). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:

    Умножим 3-ую строку на (3). Умножим 4-ую строку на (-2). Добавим 4-ую строку к 3-ой:

    Добавим 2-ую строку к 1-ой:

    Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:

    Добавим 2-ую строку к 1-ой:

    3x2 -2x3 – 3x4 = 10
    3x1 -x2 -2x3 = 1
    Необходимо переменные x3,x4 принять в качестве свободных переменных и через них выразить базисные – x1, x2.
    Ранг основной матрицы равен 2. Ранг расширенной матрицы тоже равен 2. Система совместна и имеет бесконечное множество решений.

    Читайте также:  Какие способы экономии энергии вам известны кратко

    Пример №3 . Дана система линейных уравнений у которой число уравнений равно числу неизвестных. При каком условии эта система имеет единственное решение?
    Ответ: Система имеет единственное решение, если ранг этой системы будет равен количеству переменных.

    Источник

    ЕГЭ2022 (математика профиль) в ВК

    Скоро вебинар
    «ПРЯМАЯ НА ПЛОСКОСТИ»
    (Аналитическая геометрия). Жми подробнее.

    Теорема Кронекера-Капелли. Метод Гаусса.

    «Если Вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.»
    Д. Пойа (1887-1985 г.)

    (Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)

    Пусть дана система m линейных уравнений с n неизвестными

    .

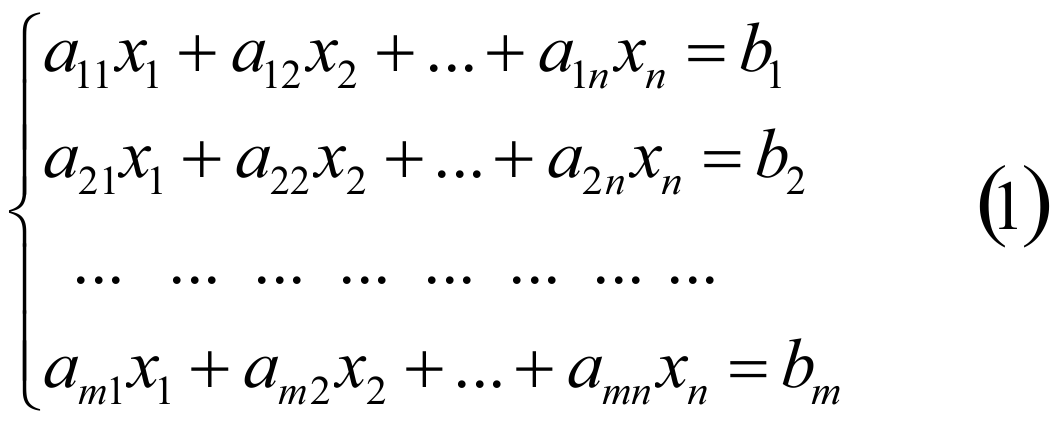
    На вопрос о совместности этой системы дает теорема Кронекера-Капелли.

    Какая система называется совместной читать здесь

    Теорема Кронекера-Капелли: Система линейных уравнений (СЛУ) совместна тогда и только тогда, когда ранг расширенной матрицы системы (rp) равен рангу основной матрицы (ro).

    Что называется расширенной матрицей читать здесь

    Что такое ранг матрицы и как его найти читать здесь

    Правила отыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем.

    Теорема 1: Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.

    Теорема 2: Если ранг совместной системы меньше числа неизвестных, то система имеет бесконечно много решений.

    МЕТОД ГАУССА

    Одним из наиболее универсальных и эффективных методов решения СЛУ является МЕТОД ГАУССА, состоящий в последовательном исключении неизвестных.

    СУЩНОСТЬ МЕТОДА ГАУССА. Расширенную матрицу системы с помощью элементарных преобразований приводят к ступенчатой, восстанавливают систему, которая является равносильной исходной системе, и находят решение.

    Как данную матрицу привести к ступенчатой читать здесь

    Рассмотрим этот метод на примерах.

    ПРИМЕР 1:

    РЕШЕНИЕ:

    Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.

    Ранг основной матрицы равен 2 (ro=2), а ранг расширенной – 3 (rp=3), поэтому по теореме Кронекера-Капелли система несовместна.

    (Последняя строка представляет собой уравнение вида: 0=1. Поэтому делаем вывод, что система несовместна.)

    Ответ: система несовместна.

    Замечание: Если хотя бы одна строка имеет вид:

    то система несовместна.

    ПРИМЕР 2:

    ro=rp=3, поэтому по теореме Кронекера-Капелли система совместна, причем ранг системы равен числу неизвестных, следовательно система имеет единственное решение.

    Ответ: (4;1;-5)

    ПРИМЕР 3:

    РЕШЕНИЕ:

    Третья и четвертая строки получились нулевыми. Их можно вычеркнуть.

    ro=rp=2, поэтому по теореме Кронекера-Капелли система совместна, причем ранг системы меньше числа неизвестных, следовательно система имеет бесконечное число решений.

    Ответ:

    В открывшемся окне:

    • поставить галочку возле «Добавить сообщение получателю»
    • в появившемся поле оставить сообщение «в дар» или «подарок».

    ИЛИ

  • оставить комментарий ниже.

    • Упражнения к уроку:

    Решите системы методом Гаусса

    ;
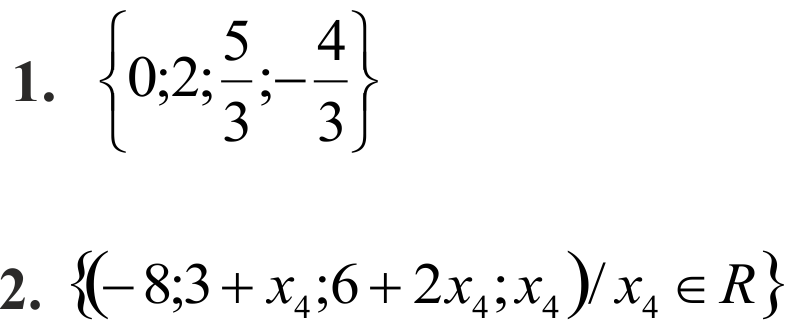
    3.Система несовместна.

    Автор: Аникина Анна

    Комментарии к этой заметке:

    Добавить Ваш комментарий

    Хотите внести свою лепту в его развитие!? Тогда Вам сюда!

    Источник

    учимся
    программировать

    Программированию нельзя научить, можно только научится

    Главная » Уроки по Численным методам » Урок 14. Решение систем линейных уравнений (СЛУ). Теорема Кронекера-Капелли. Решение СЛУ с помощью матричных уравнений

    Урок 14. Решение систем линейных уравнений (СЛУ). Теорема Кронекера-Капелли. Решение СЛУ с помощью матричных уравнений

    Система линейных уравнений:

    (1)

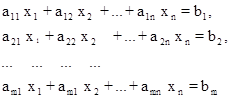
    Здесь и (i =1..m, j=1..n) — заданные, а — неизвестные действительные числа.
    Матричной записью системы линейных уравнений называется выражение вида:
    =, или кратко: = (2),
    где:

    =

    =

    столбец свободных членов

    Упорядоченная совокупность n вещественных чисел (c1, c2. cn) называется решением системы(1), если в результате подстановки этих чисел вместо соответствующих переменных x1, x2. xn каждое уравнение системы обратится в арифметическое тождество; другими словами, если существует вектор C= (c1, c2. cn)T такой, что AC = B.

    СЛУ называется совместной, или разрешимой, если она имеет, по крайней мере, одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.
    Матрица
    ,
    образованная путем приписывания справа к матрице A столбца свободных членов, называется расширенной матрицей системы.

    Вопрос о совместности системы (1) решается следующей теоремой.

    Теорема Кронекера-Капелли

    Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы.

    Система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

    Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.

    Пример. Исследовать систему линейных уравнений

    Решение. Составим расширенную матрицу системы и с помощью элементарных преобразований вычислим одновременно ранги обеих матриц.

    Далее умножим вторую строку на -2 и сложим с третьей, а затем сложим третью строку с последней. Имеем
    .
    Ранг матрицы системы =3, так как матрица имеет три ненулевых строки,
    а ранг расширенной матрицы =4.
    Тогда согласно теореме Кронекера-Капелли система не имеет решений.

    Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, — так называемые системы крамеровского типа:
    a11 x1 + a12 x2 +. + a1n xn = b1,
    a21 x1 + a22 x2 +. + a2n xn = b2, (3)
    . . . . . .
    an1 x1 + an1 x2 +. + ann xn = bn.

    Системы (3) решаются одним из следующих способов:
    1) методом Гаусса, или методом исключения неизвестных;
    2) по формулам Крамера;
    3) матричным методом.

    Матричный метод

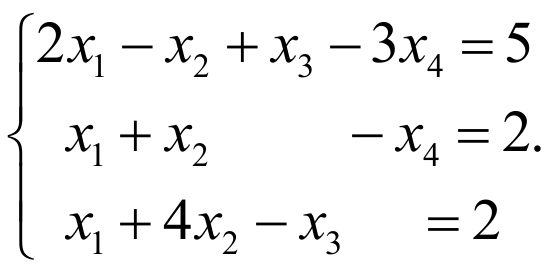
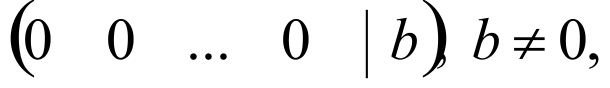
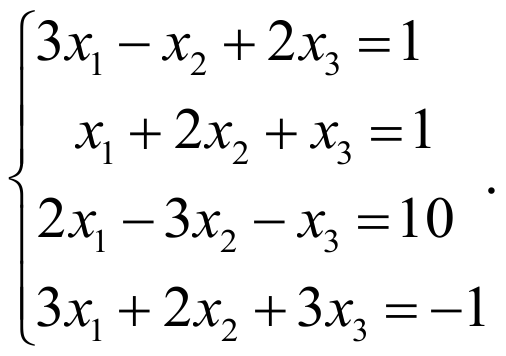
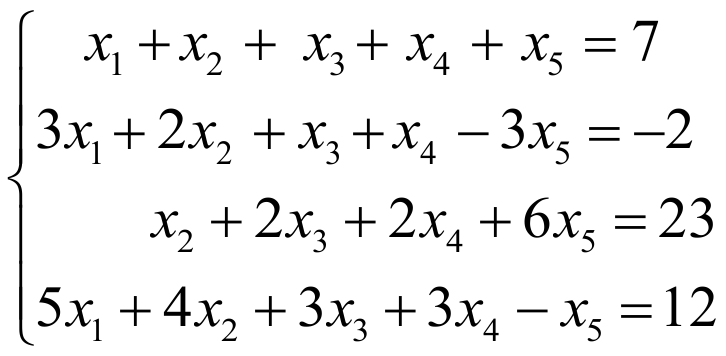
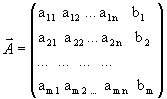    Если матрица А системы линейных уравнений невырожденная, т.е. det A=0, то матрица А имеет обратную, и решение системы (3) совпадает с вектором . Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X=C, C=A-1B называют матричным способом решения системы, или решением по методу обратной матрицы.

    Задание 1: Решить систему уравнений матричным способом в Excel

    Ход решения:

    1. Сначала надо записать систему в матричном виде и ввести ее на лист Excel:

    , здесь ,

    1. Затем надо с помощью Excel найти обратную матрицу для матрицы А.
    2. Далее полученную матрицу нужно умножить на матрицу В.
    3. В результате получим ответ:

    Задание 2: Самостоятельно решить матричным способом систему уравнений

    Ответ для самопроверки:

    Источник

    Оцените статью
    Разные способы
    © 2024 Разные способы.
    Внимание! Информация, опубликованная на сайте, носит исключительно ознакомительный характер и не является рекомендацией к применению.
    =