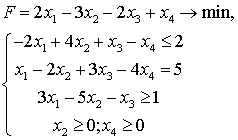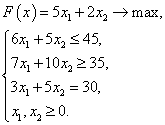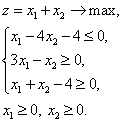Способ решения двойственных задач

Решение двойственной задачи

Здесь мы рассмотрим вопрос, как из решения прямой задачи, получить решение двойственной задачи.

Теоремы двойственности

Первая теорема двойственности

Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная задача имеет оптимальное решение. При этом значения целевых функций прямой и двойственной задачи, для оптимальных решений, равны друг другу.

Если одна из пары двойственных задач не имеет решения вследствие неограниченности целевой функции, то двойственная задача не имеет решения вследствие несовместимости системы ограничений.

Вторая теорема двойственности

Пусть мы имеем симметричную пару двойственных задач (1) и (2):
(1.1) ;
(1.2)
(2.1) ;
(2.2)
Для того чтобы допустимые решения и являлись оптимальными решениями двойственных задач (1) и (2), необходимо и достаточно, чтобы выполнялись следующие равенства:
(3) , .
(4) , ;

Для наглядности, выпишем равенства (3) и (4) в развернутом виде:
(3.1)
(3.2)

(3.m)

Метод решения двойственной задачи

Применяя теоремы двойственности, можно получить решение двойственной задачи из решения прямой. Опишем метод решения двойственной задачи.

Пусть мы нашли решение прямой задачи (1) с оптимальным значением целевой функции и с оптимальным планом . Подставим найденные значения в систему ограничений (1.2). Тогда если -е неравенство не является равенством, то есть если
,
то, согласно (3.i),
.
Рассматривая все строки системы ограничений (1.2), мы найдем, что часть переменных двойственной задачи равна нулю.

Далее замечаем, что если , то, согласно (4.k), -я строка системы ограничений (2.2) является равенством:
.
Составив все строки системы ограничений (2.2), для которых , мы получим систему уравнений, из которой можно найти ненулевые значения переменных .

На основании первой теоремы двойственности, минимальное значение целевой функции
.

Если известно решение задачи (2), то аналогичным образом можно найти решение задачи (1).

Примеры решения двойственной задачи из решения прямой

Пример 1

Пусть дана задача линейного программирования:
;

Известно решение этой задачи:
; .

Составить двойственную задачу и получить ее решение из решения прямой.

Согласно первой теореме двойственности, оптимальное значение целевой функции равно
.

Применим вторую теорему двойственности. Подставим оптимальные значения переменных в систему ограничений прямой задачи.
(П1.1.1) ;
(П1.1.2) ;
(П1.1.3) ;
(П1.1.4) .
Поскольку первая и четвертая строки являются строгими неравенствами (не являются равенствами), то
и .

Поскольку и , то 2-я и 4-я строки двойственной задачи являются равенствами:

Подставим уже найденные значения и , имеем:

Отсюда
;
; .

Двойственная задача имеет вид:
;

Ее решение
;

Пример 2

Дана задача линейного программирования:
(П2.1.1) ;
(П2.1.2)
Найти решение этой задачи, решив двойственную задачу графическим методом.

Решение задачи (П2.2) приводится на странице “Решение задач линейного программирования графическим методом”. Решение задачи (П2.2) имеет вид:
; .

Согласно первой теореме двойственности, оптимальное значение целевой функции равно
.

Применим вторую теорему двойственности. Подставим оптимальные значения переменных в систему ограничений прямой задачи (П2.2).
;
;
.
Поскольку третья строка является строгим неравенством (не являются равенством), то
.

Поскольку и , то 1-я и 2-я строки двойственной задачи (П2.1) являются равенствами:

Подставим найденное значение .

Решаем систему уравнений.
;
;
;
; ;
.

Решение исходной задачи (П2.1) имеет вид:
; .

Автор: Олег Одинцов . Опубликовано: 27-08-2016

Источник

Двойственные задачи линейного программирования

Двойственность является важным понятием в линейном программировании, имеющим экономическое (практическое) применение. Например, для задачи оптимального распределения ресурсов для производства некоторых видов товаров пара прямой и двойственной задачи принимает следующий экономический смысл:
Прямая задача: Сколько и какой продукции xj необходимо производить, чтобы при заданных доходах Cj и объемах ресурсов bi максимизировать доход от продажи продукции?
Двойственная задача: Какова должна быть «теневая» цена каждого ресурса yi, чтобы при заданных количествах bi и доходах Cj минимизировать затраты?

Для составления двойственных задач используют специальные правила, при решении же выбирают один из наиболее подходящих методов решения ЗЛП: симплекс-метод, графический метод. Более того, так как между парой двойственных задач существует связь, иногда достаточно решить только одну из задач, чтобы получить решение второй.

Примеры составления и решения двойственных задач линейного программирования приведены в этом разделе — изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении подобных заданий — Решение контрольных по линейному программированию.

Примеры составления и решения двойственных задач онлайн

Задача 1. Записать математическую модель двойственной ЗЛП по заданной прямой:

Задача 2. Составить задачу, двойственную исходной задаче:

Задача 3. Решить задачу линейного программирования; составить задачу, двойственную данной, и также найти ее решение:

Источник

Двойственная задача линейного программирования. Онлайн калькулятор

С помощю этого онлайн калькулятора можно построить двойственную задачу линейного программирования (ЛП) по отношению к исходной задаче. Для построения двойственной задачи, введите данные исходной задачи и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Запись

1. Построение двойственной задачи к исходной задаче линейного программирования

Пусть задана прямая задача линейного программирования (ЛП) в общем виде:

(1a)

(1b)

(1c)

(1d)

(1e)

Задаче (1) соответствует следующая двойственная задача ЛП:

(2a)

(2b)

(2c)

(2d)

(2e)

В этих задачах знак ∀ — определяет, что на данную переменную не налагается ограничение в виде неотрицательности, т.е. она произвольная.

Отметим, что если задача ЛП (2) является двойственной к задаче ЛП (1), то задача ЛП (1) является двойственной к задаче ЛП (2). Говорят, что задачи ЛП (1) и (2) взаимно двойственные задачи линейного программирования.

Рассмотрим подробно процесс построения двойственной задачи к исходной задачи линейного программирования. Для построения двойственной задачи:

1. Упорядочивается запись исходной задачи ЛП: если целевая функция исследуется на максимум, то ограничения (1b), (1c) должны иметь знак или «=», или «≤», а если целевая функция исследуется на минимум, то ограничения (1b), (1c) должны иметь знак или «=» , или «≥». Если в исходной задаче ЛП есть ограничения, не удовлетворяющие этим условиям, то это можно исправить, умножая данное ограничение на −1.

2. Каждому ограничению исходной задачи ставится в соответствие переменная . Число переменных двойственной задачи равно числу ограничений исходной задачи, а число ограничений двойственной задачи равно числу переменных исходной задачи.

3. Если в исходной задаче целевая функция исследуется на максимум, то целевая функция двойственной задачи исследуется на минимум.

4. Свободные члены исходной задачи становятся коэффициентами целевой функции двойственной задачи.

5. Коэффициенты целевой функции исходной задачи становятся свободными членами двойственной задачи.

6. Матрица коэффициентов двойственной задачи получается транспонированием матрицы коэффициентов исходной задачи.

7. Если на переменную наложено ограничение в виде неотрицательности, то j-е ограничение двойственной задачи записывается в виде неравенства. Если же переменная исходной задачи произвольная, то j-е ограничение двойственной задачи имеет знак равенства.

8. Если в исходой задаче имеются ограничения в виде равенств, то на соответствующие переменные двойственной задачи не налагаются условия неотрицательности.

Чтобы посмотреть пример построения двойственной задачи воспользуйтесь онлайн калькулятором в начале страницы. Для этого введите коэффициенты исходной задачи в ячейки калькулятора и нажмите на кнопку «Построить».

2. Теория двойственности в задачах линейного программирования

Утверждение 1. Если X и Y − допустимые точки задач (1) и (2), соответственно, то

.

(3)

При этом, если для каких то допустимых точек и выполнено равенство , то и являются решениями задач (1) и (2) соответственно.

Доказательство. Запишем взвимно двойственные задачи (1) и (2) в матричном виде.

(4a)

(4b)

(4c)

(4d)

где ,,,,,,

матрица коэффициентов ограничений исходной задачи, которая разделена на четыре матрицы следующих порядков: ,,,.

Сделаны также следующие обозначения:

, ,

(5a)

(5b)

(5c)

(5d)

где , , .

(6)

(5b) и (5c) можно записать так:

,

(7)

Легко показать, что

(8)

(9)

Множители в правой части выражения (9) неотрицательны. Тогда их произведение не отрицательно, т.е. выполнено условие (8).

Учитывая (7) и (8) упростим выражение 6:

(9)

С другой стороны:

(10)

(11)

(4b) и (4c) можно записать так

(12)

Учитывая (12) и Y₁ упростим выражение (11):

(13)

Из (9) и (13) получим:

(14)

т.е. выполнено условие (3).

Докажем вторую часть утверждения 1. Для любой допустимой точки x задачи (1) в том числе . Тогда

Поэтому наибольшее значение целевой функции задачи (1).

С другой стороны для любой допустимой точки y задачи (2)

т.е. − наименьшее из значений целевой функции задачи (2). Таким образом получили, что является решением задачи (1), а является решением задачи (2).

Теорема 1 (первая теорема двойственности). Если исходная задача имеет решение , то двойственная ей задача также имеет решение , и

.

Если в исходной задаче целевая функция неограничена, то в двойственной задаче допустимая область пуста.

Отметим, что обратное утверждение неверно. Из несовместности системы системы ограничений одной из задач не следует неограниченность целевой функции для другой. В этом случае системы ограничений обеих задач могут быть несовместными. Приведем пример.

Представленные задачи взаимно двойственные, и в этих задачах допустимые области пусты.

Теорема 2 (вторая теорема двойственности или условие дополняющей нежесткости). Планы и пары двойственных задач (1) и (2) являются решениями этих задач тогда и только тогда, когда выполняются следующие условия:

(15)

,

(16)

или выполняется условие:

.

(17)

Докажем эквивалентность условий (15) и (16) с условием (17).

Из (4с) и (5с) имеем:

, .

(18)

,

(19)

.

(20)

Из (15) и (16) имеем:

.

(21)

,

(22)

Подставляя (19),(20) в (21),(22) соответственно и упрощая получим:

,

(23)

,

(24)

Выразив, например, через остальные слагаемые из (23) и подставляя в (24) получим:

.

(25)

А Запись (25) − это другой вид записи равенства (17).

3. Двойственные к разным формам задач линейного программирования

В статье Формы записи задачи линейного программирования мы рассмотрели различные формы записи задачи линейного программирования. В этом параграфе мы рассмотрим двойственные задачи к задачам ЛП в различных формах.

1) Двойственной к задаче ЛП в канонической форме

,

является задача ЛП в основной форме

2) Двойственной к задаче ЛП в основной форме

является задача ЛП в канонической форме

3) Двойственной к задаче ЛП в стандантной форме

является задача ЛП также в стандартной форме

Все эти три пары взаимно двойственных задач получаются из пары двойственных задач в общем виде (1) и (2) при различных значениях n₁ и m₁. Первая пара задач получается из (1) и (2) при m₁=0, n₁=n. Вторая пара задач получается из задач (1) и (2) при m₁=m, n₁=0. Третья пара задач получается из (1) и (2) при m₁=m, n₁=n.

Иногда более удобно рассматривать задачи ЛП в векторно-матричной форме. Высше представленные пары двойственных задач представим в векторно-матричной форме записи.

1) Двойственной к задаче ЛП в канонической форме

является задача ЛП в основной форме

.

2) Двойственной к задаче ЛП в основной форме

является задача ЛП в канонической форме

.

3) Двойственной к задаче ЛП в стандантной форме

.

является задача ЛП также в стандартной форме

.

где векторы строки порядка и соответственно, векторы-столбцы порядка и соответственно, − матрица порядка .

4.Условие дополняющей нежесткости

Равенства (15) и (16) называются условиями дополняющей нежесткости. Рассмотрим уравнение (16). Левая часть уравнения является скалярным произведением неотрицательных векторов и , а это означает, что если один из координат одного из этих векторов больше нуля, то соответствующая координата другого вектора равна нулю (поскольку их скалярное произведение равно нулю). Получается, что если в системе линейных неравенств (4b) некоторое неравенство в точке не удовлетворяется как равенство, то соответствующая координата вектора равна нулю и обратно − если некоторая координата вектора больше нуля, то соответствующее неравенство в системе (4b) в точке удовлетворяется как равенство.

Аналогичные рассуждения можно привести и для равенства (15). Условие дополняющей нежесткости позволяет найти оптимальный план двойственной задачи, если известен оптимальный план исходной задачи. Рассмотрим это на примере пар двойственных задач ЛП записанных в стандартной форме.

Пример 1. Дана следующая задача ЛП:

(26a)

(26b)

(26c)

(26d)

Решить данную задачу. Построить двойственную задачу и найти ее решение используя решение исходной задачи.

Запишем задачу ЛП в матричном виде:

, , , .

Поскольку задача с двумя переменными, то ее можно решить графически.

Как видно из рисунка, область определения – это желтая область . Вектор целевой функции c=<1;2>. Для нахождения оптимального плана нужно прямую, перпендикулярную вектору С перемешать по направлению вектора С , до предельного положения соприкосающаяся с областью определения (точка M). Таким образом точка M является оптимальным решением задачи линейного программирования. Как видно из рисунка, точка M находится на пересечении следующих прямых:

(27)

Решая систему линейных уравнений (27) получим координаты точки M, т.е. оптимальный план задачи ЛП (26):

(28)

или в векторном виде:

(29)

Целевая функция в этой точке равна:

Построим двойственную к (26) задачу ЛП:

(30a)

(30b)

(30c)

(30d)

В векторно матричном виде задача ЛП (30) будет выглядеть так:

Условие дополняющей нежесткости (15) и (16) в случае задач ЛП в стандартной форме примут вид:

,

(31)

.

(32)

Условие (32) позволяет найти оптимальный план двойственной задачи ЛП (30). Поскольку все координаты оптимального плана исходной задачи положительны, то из равенства (32) следует, что неравенства (30b) и (30c) в оптимальной точке должны выполняться как равенства, т.е. надо решить систему линейных уравнений

Решив данное уравнение находим оптимальный план

.

Найдем значение целевой функции в данной точке:

.

Значение целевых функций в оптимальных точках исходной и двойственной задач равны. Следовательно получено правильное решение.

Графический метод решения задачи ЛП (30) смотрите на Рис.2:

Рассмотрим пример с той же допустимой областью, что и пример 1, но с другой целевой функцией.

Пример 2. Дана следующая задача ЛП:

(33a)

(33b)

(33c)

(33d)

Решить данную задачу. Построить двойственную задачу и найти ее решение используя решение исходной задачи и условия дополняющей нежесткости.

Запишем задачу ЛП в матричном виде:

, , , .

Поскольку задача с двумя переменными, то ее можно решить графически.

Из Рис.3 видно, что оптимальным является точка

Целевая функция в этой точке равна:

Построим двойственную задачу:

(34a)

(34b)

(34c)

(34d)

В оптимальной точке ограничение (33b) удовлетворяется как строгое неравенство следовательно исходя из условия дополняющей нежесткости (31), первая координата вектора должна быть равна нулю: . Из равенства (32) следует, что неравенство (34b) в оптимальной точке должно выполняться как равенство, поскольку соответствующая координата опттимального плана исходной задачи больше нуля. Таким образом имеем систему линейных уравнений:

Откуда получим .

В векторном виде оптимальный план двойственной задачи имеет вид:

.

Найдем значение целевой функции в данной точке:

.

Значение целевых функций в оптимальных точках исходной и двойственной задач равны. Следовательно получено правильное решение.

Графический метод решения задачи ЛП (34) представлен на Рис.4. Прямая, ортогональная к вектору целевой функции B перемещаем перпендикулярно к вектору целевой функции до соприкосновения к допустимой области задачи ЛП (желтая область). Полученная точка M является решением задачи ЛП.

Источник