Способ разрешения коллизий упорядоченный список с логарифмическим поиском

Разрешение коллизий

Разрешение коллизий (англ. collision resolution) в хеш-таблице, задача, решаемая несколькими способами: метод цепочек, открытая адресация и т.д. Очень важно сводить количество коллизий к минимуму, так как это увеличивает время работы с хеш-таблицами.

Содержание

Разрешение коллизий с помощью цепочек [ править ]

Каждая ячейка [math]i[/math] массива [math]H[/math] содержит указатель на начало списка всех элементов, хеш-код которых равен [math]i[/math] , либо указывает на их отсутствие. Коллизии приводят к тому, что появляются списки размером больше одного элемента.

В зависимости от того нужна ли нам уникальность значений операции вставки у нас будет работать за разное время. Если не важна, то мы используем список, время вставки в который будет в худшем случае равна [math]O(1)[/math] . Иначе мы проверяем есть ли в списке данный элемент, а потом в случае его отсутствия мы его добавляем. В таком случае вставка элемента в худшем случае будет выполнена за [math]O(n)[/math]

Время работы поиска в наихудшем случае пропорционально длине списка, а если все [math]n[/math] ключей захешировались в одну и ту же ячейку (создав список длиной [math]n[/math] ) время поиска будет равно [math]\Theta(n)[/math] плюс время вычисления хеш-функции, что ничуть не лучше, чем использование связного списка для хранения всех [math]n[/math] элементов.

Удаления элемента может быть выполнено за [math]O(1)[/math] , как и вставка, при использовании двухсвязного списка.

Линейное разрешение коллизий [ править ]

Все элементы хранятся непосредственно в хеш-таблице, без использования связных списков. В отличие от хеширования с цепочками, при использовании этого метода может возникнуть ситуация, когда хеш-таблица окажется полностью заполненной, следовательно, будет невозможно добавлять в неё новые элементы. Так что при возникновении такой ситуации решением может быть динамическое увеличение размера хеш-таблицы, с одновременной её перестройкой.

Стратегии поиска [ править ]

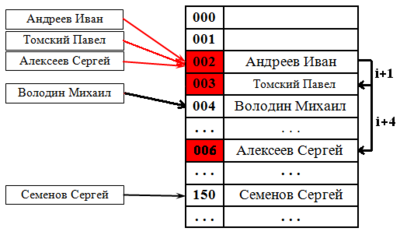
При попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math]i+1, i+2, i+3[/math] и так далее, пока не найдём свободную ячейку. В неё и запишем элемент.

Выбираем шаг [math]q[/math] . При попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math]i+(1 \cdot q), i+(2 \cdot q), i+(3 \cdot q)[/math] и так далее, пока не найдём свободную ячейку. В неё и запишем элемент. По сути последовательный поиск — частный случай линейного, где [math]q=1[/math] .

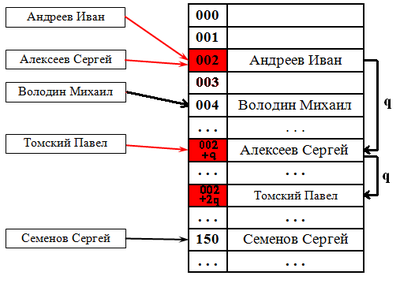
Шаг [math]q[/math] не фиксирован, а изменяется квадратично: [math]q = 1,4,9,16. [/math] . Соответственно при попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math] i+1, i+4, i+9[/math] и так далее, пока не найдём свободную ячейку.

Проверка наличия элемента в таблице [ править ]

Проверка осуществляется аналогично добавлению: мы проверяем ячейку [math]i[/math] и другие, в соответствии с выбранной стратегией, пока не найдём искомый элемент или свободную ячейку.

При поиске элемента может получится так, что мы дойдём до конца таблицы. Обычно поиск продолжается, начиная с другого конца, пока мы не придём в ту ячейку, откуда начинался поиск.

Проблемы данных стратегий [ править ]

Проблем две — крайне нетривиальное удаление элемента из таблицы и образование кластеров — последовательностей занятых ячеек.

Кластеризация замедляет все операции с хеш-таблицей: при добавлении требуется перебирать всё больше элементов, при проверке тоже. Чем больше в таблице элементов, тем больше в ней кластеры и тем выше вероятность того, что добавляемый элемент попадёт в кластер. Для защиты от кластеризации используется двойное хеширование и хеширование кукушки.

Удаление элемента без пометок [ править ]

Рассуждение будет описывать случай с линейным поиском хеша. Будем при удалении элемента сдвигать всё последующие на [math]q[/math] позиций назад. При этом:

• если в цепочке встречается элемент с другим хешем, то он должен остаться на своём месте (такая ситуация может возникнуть если оставшаяся часть цепочки была добавлена позже этого элемента)
• в цепочке не должно оставаться «дырок», тогда любой элемент с данным хешем будет доступен из начала цепи

Учитывая это будем действовать следующим образом: при поиске следующего элемента цепочки будем пропускать все ячейки с другим значением хеша, первый найденный элемент копировать в текущую ячейку, и затем рекурсивно его удалять. Если такой следующей ячейки нет, то текущий элемент можно просто удалить, сторонние цепочки при этом не разрушатся (чего нельзя сказать про случай квадратичного поиска).

Хеш-таблицу считаем зацикленной

Утверждение (о времени работы):

[math]\triangleright[/math]

Заметим что указатель [math]j[/math] в каждой итерации перемещается вперёд на [math]q[/math] (с учётом рекурсивных вызовов [math]\mathrm[/math] ). То есть этот алгоритм последовательно пройдёт по цепочке от удаляемого элемента до последнего — с учётом вызова [math]\mathrm[/math] собственно для нахождения удаляемого элемента, мы посетим все ячейки цепи.

[math]\triangleleft[/math]

Вариант с зацикливанием мы не рассматриваем, поскольку если [math]q[/math] взаимнопросто с размером хеш-таблицы, то для зацикливания в ней вообще не должно быть свободных позиций

Теперь докажем почему этот алгоритм работает. Собственно нам требуется сохранение трёх условий.

• В редактируемой цепи не остаётся дырок

Докажем по индукции. Если на данной итерации мы просто удаляем элемент (база), то после него ничего нет, всё верно. Если же нет, то вызванный в конце [math]\mathrm[/math] (см. псевдокод) заметёт созданную дыру (скопированный элемент), и сам, по предположению, новых не создаст.

• Элементы, которые уже на своих местах, не должны быть сдвинуты.

• В других цепочках не появятся дыры

Противное возможно только в том случае, если какой-то элемент был действительно удалён. Удаляем мы только последнюю ячейку в цепи, и если бы на её месте возникла дыра для сторонней цепочки, это бы означало что элемент, стоящий на [math]q[/math] позиций назад, одновременно принадлежал нашей и другой цепочкам, что невозможно.

Двойное хеширование [ править ]

Двойное хеширование (англ. double hashing) — метод борьбы с коллизиями, возникающими при открытой адресации, основанный на использовании двух хеш-функций для построения различных последовательностей исследования хеш-таблицы.

Принцип двойного хеширования [ править ]

При двойном хешировании используются две независимые хеш-функции [math] h_1(k) [/math] и [math] h_2(k) [/math] . Пусть [math] k [/math] — это наш ключ, [math] m [/math] — размер нашей таблицы, [math]n \bmod m [/math] — остаток от деления [math] n [/math] на [math] m [/math] , тогда сначала исследуется ячейка с адресом [math] h_1(k) [/math] , если она уже занята, то рассматривается [math] (h_1(k) + h_2(k)) \bmod m [/math] , затем [math] (h_1(k) + 2 \cdot h_2(k)) \bmod m [/math] и так далее. В общем случае идёт проверка последовательности ячеек [math] (h_1(k) + i \cdot h_2(k)) \bmod m [/math] где [math] i = (0, 1, \; . \;, m — 1) [/math]

Таким образом, операции вставки, удаления и поиска в лучшем случае выполняются за [math]O(1)[/math] , в худшем — за [math]O(m)[/math] , что не отличается от обычного линейного разрешения коллизий. Однако в среднем, при грамотном выборе хеш-функций, двойное хеширование будет выдавать лучшие результаты, за счёт того, что вероятность совпадения значений сразу двух независимых хеш-функций ниже, чем одной.

[math]\forall x \neq y \; \exists h_1,h_2 : p(h_1(x)=h_1(y))\gt p((h_1(x)=h_1(y)) \land (h_2(x)=h_2(y)))[/math]

Выбор хеш-функций [ править ]

[math] h_1 [/math] может быть обычной хеш-функцией. Однако чтобы последовательность исследования могла охватить всю таблицу, [math] h_2 [/math] должна возвращать значения:

• не равные [math] 0 [/math]
• независимые от [math] h_1 [/math]
• взаимно простые с величиной хеш-таблицы

Есть два удобных способа это сделать. Первый состоит в том, что в качестве размера таблицы используется простое число, а [math] h_2 [/math] возвращает натуральные числа, меньшие [math] m [/math] . Второй — размер таблицы является степенью двойки, а [math] h_2 [/math] возвращает нечетные значения.

Например, если размер таблицы равен [math] m [/math] , то в качестве [math] h_2 [/math] можно использовать функцию вида [math] h_2(k) = k \bmod (m-1) + 1 [/math]

Пример [ править ]

Показана хеш-таблица размером 13 ячеек, в которой используются вспомогательные функции:

[math] h(k,i) = (h_1(k) + i \cdot h_2(k)) \bmod 13 [/math]

[math] h_1(k) = k \bmod 13 [/math]

[math] h_2(k) = 1 + k \bmod 11 [/math]

Мы хотим вставить ключ 14. Изначально [math] i = 0 [/math] . Тогда [math] h(14,0) = (h_1(14) + 0\cdot h_2(14)) \bmod 13 = 1 [/math] . Но ячейка с индексом 1 занята, поэтому увеличиваем [math] i [/math] на 1 и пересчитываем значение хеш-функции. Делаем так, пока не дойдем до пустой ячейки. При [math] i = 2 [/math] получаем [math] h(14,2) = (h_1(14) + 2\cdot h_2(14)) \bmod 13 = 9 [/math] . Ячейка с номером 9 свободна, значит записываем туда наш ключ.

Таким образом, основная особенность двойного хеширования состоит в том, что при различных [math] k [/math] пара [math] (h_1(k),h_2(k)) [/math] дает различные последовательности ячеек для исследования.

Простая реализация [ править ]

Пусть у нас есть некоторый объект [math] item [/math] , в котором определено поле [math] key [/math] , от которого можно вычислить хеш-функции [math] h_1(key)[/math] и [math] h_2(key) [/math]

Так же у нас есть таблица [math] table [/math] величиной [math] m [/math] , состоящая из объектов типа [math] item [/math] .

Реализация с удалением [ править ]

Чтобы наша хеш-таблица поддерживала удаление, требуется добавить массив [math]deleted[/math] типов [math]bool[/math] , равный по величине массиву [math]table[/math] . Теперь при удалении мы просто будем помечать наш объект как удалённый, а при добавлении как не удалённый и замещать новым добавляемым объектом. При поиске, помимо равенства ключей, мы смотрим, удалён ли элемент, если да, то идём дальше.

Альтернативная реализация метода цепочек [ править ]

В Java 8 для разрешения коллизий используется модифицированный метод цепочек. Суть его заключается в том, что когда количество элементов в корзине превышает определенное значение, данная корзина переходит от использования связного списка к использованию сбалансированного дерева. Но данный метод имеет смысл лишь тогда, когда на элементах хеш-таблицы задан линейный порядок. То есть при использовании данный типа [math]\mathbf[/math] или [math]\mathbf[/math] имеет смысл переходить к дереву поиска, а при использовании каких-нибудь ссылок на объекты не имеет, так как они не реализуют нужный интерфейс. Такой подход позволяет улучшить производительность с [math]O(n)[/math] до [math]O(\log(n))[/math] . Данный способ используется в таких коллекциях как HashMap, LinkedHashMap и ConcurrentHashMap.

Источник

Лабораторная работа № 1
Работа с таблицей символов

Цель работы: изучить основные методы организации таблиц идентификаторов, получить представление о преимуществах и недостатках, присущих различным методам организации таблиц идентификаторов (таблиц символов или таблиц имен).

Краткие теоретические сведения

Назначение таблицы идентификаторов

Проверка правильности семантики и генерация кода требуют знания характеристик идентификаторов, используемых в программе на исходном языке. Эти характеристики выясняются из описаний и из того, как идентификаторы используются в программе и накапливаются в таблице символов (или таблице идентификаторов).

Любая таблица идентификаторов состоит из набора полей (ячеек таблицы), количество которых совпадает с количеством различных идентификаторов в исходной программе. Каждое поле содержит полную информацию об идентификаторе, которому соответствует данный элемент таблицы. Под идентификаторами подразумеваются имена констант, переменных, модулей, процедур и функций, а также формальные параметры процедур и функций. Компилятор может работать с одной или несколькими таблицам идентификаторов – их количество зависит от реализации компилятора.

Вне зависимости от реализации компилятора принцип его работы с таблицей идентификаторов остается одним и тем же – на различных фазах компиляции XE «Фаза компиляции» компилятор многократно обращается к этой таблице для поиска информации и записи новых данных. Причем поиск данных в таблице выполняется существенно чаще, чем запись в таблицу новых данных, поскольку в исходной программе использование ранее описанных идентификаторов встречается существенно чаще, чем описания новых идентификаторов, да и для каждого встреченного описания компилятор должен проверить существование такого же идентификатора, чтобы исключить дублирование их имен.

Отсюда можно сделать вывод, что таблицы идентификаторов должны быть организованы таким образом, чтобы компилятор имел возможность максимально быстрого поиска нужного ему элемента. Каждый элемент таблицы идентификаторов характеризуется уникальным именем. Даже в том случае, когда исходный язык допускает совпадающие имена идентификаторов – например, при различных областях видимости идентификаторов – в компиляторе существуют средства обеспечения уникальности их имен в пределах всей исходной программы. Поэтому поиск элемента в таблице выполняется по имени идентификатора, которое считается уникальным в пределах одной таблицы идентификаторов.

Простейшие способы организации таблицы идентификаторов

Таблица идентификаторов в виде простого линейного списка

Самый простой способ организации таблицы идентификаторов состоит в том, чтобы добавлять элементы в таблицу в порядке их поступления. В этом случае таблица идентификаторов будет представлять собой простой линейный список или массив с переменным количеством элементов. Тогда добавление нового элемента (нового идентификатора) в таблицу практически не будет требовать затрат вычислительных ресурсов – время записи нового элемента пренебрежимо мало: T _з

0. Но поиск идентификатора в таблице в этом случае потребует последовательного сравнения искомого элемента с каждым элементом таблицы, пока не будет найден подходящий. Для таблицы, содержащей N элементов, в среднем будет выполнено N /2 сравнений – тогда время поиска можно оценить как: T _п

N /2. Если N велико, то этот способ нельзя признать эффективным.

Таблица идентификаторов в виде упорядоченного списка

Поиск может быть выполнен более эффективно, если элементы таблицы упорядочены (отсортированы) согласно некоторому естественному порядку. В данном случае, когда поиск будет осуществляться по имени идентификатора, наиболее естественным будет расположить элементы таблицы в алфавитном порядке. Эффективным методом поиска в упорядоченном списке из N элементов является бинарный или логарифмический поиск. Символ S, который следует найти, сравнивается с элементом в середине таблицы: ( N div 2)+1. Если они совпадают, то искомый элемент найден. Иначе, если этот элемент не является искомым (не совпадает с S ), то необходимо просмотреть только блок элементов, пронумерованных от 1 до ( N div 2), или блок элементов от ( N div 2)+2 до N в зависимости от того, меньше искомый элемент, чем S или больше. Затем эта же операция повторяется над блоком меньшего размера. Так как на каждом шаге число элементов, которые могут содержать S, сокращается в два раза, то максимальное число сравнений равно 1+[ log ₂ N ]. Тогда время поиска идентификатора можно оценить как: T _п

Для сравнения: при для N =128 бинарный поиск требует самое большее 8 сравнений, поиск в неупорядоченной таблице – в среднем 64 сравнения.

Однако для применения алгоритма бинарного поиска массив элементов должен быть упорядоченным. Это значит, что при добавлении нового идентификатора его нельзя просто добавить в конец таблицы – необходимо сначала найти место в таблице, в которое следует записать этот идентификатор, потом сдвинуть массив данных, находящихся справа от найденного места (чтобы освободить ячейку для нового элемента), и только потом записать элемент в таблицу. Таким образом, время записи нового идентификатора в таблицу можно оценить как: T _з

1+[ log ₂ N ]+ k * N /2, где k – это коэффициент, отражающий соотношение вычислительных затрат на операции сравнения и записи данных одного элемента таблицы.

Если бы операции поиска и добавления новых элементов в таблице идентификаторов выполнялись с одинаковой частотой, то преимущество метода бинарного поиска было бы ничтожным: сокращая время поиска с N /2 до 1+[ log ₂ N ] он в то же время увеличивает время добавления нового элемента с 0 до 1+[ log ₂ N ]+ k * N /2. Однако в таблице идентификаторов поиск элементов выполняется существенно чаще, чем добавление новых элементов в таблицу, поэтому применительно к таблице идентификаторов метод бинарного поиска является более эффективным, чем простой линейный список [1, 7, 13].

Таблица идентификаторов в форме бинарного дерева

Существует еще один простейший метод построения таблиц идентификаторов, при котором таблица имеет форму бинарного дерева. Каждый узел такого дерева представляет собой элемент таблицы, у которого может быть не более двух дочерних элементов, причем корневой узел является первым элементом таблицы. При построении дерева элементы сравниваются между собой, и в зависимости от результатов, выбирается путь в дереве.

Рассмотрим алгоритм XE «Алгоритм:заполнения бинарного дерева» заполнения бинарного дерева. Будем считать, что алгоритм работает с потоком входных данных, содержащим идентификаторы (в компиляторе этот поток данных порождается в процессе разбора текста исходной программы). Первый идентификатор помещается в вершину дерева. Все дальнейшие идентификаторы попадают в дерево по следующему алгоритму:

Шаг 1 . Выбрать очередной идентификатор из входного потока данных. Если очередного идентификатора нет, то построение дерева закончено.

Шаг 2 . Сделать текущим узлом дерева корневую вершину.

Шаг 3 . Сравнить очередной идентификатор с идентификатором, содержащимся в текущем узле дерева.

Шаг 4 . Если очередной идентификатор меньше, то перейти к шагу 5, если равен – сообщить об ошибке и прекратить выполнение алгоритма (двух одинаковых идентификаторов быть не должно!), иначе – перейти к шагу 7.

Шаг 5 . Если у текущего узла существует левая вершина, то сделать ее текущим узлом и вернуться к шагу 3, иначе перейти к шагу 6.

Шаг 6 . Создать новую вершину, поместить в нее очередной идентификатор, сделать эту новую вершину левой вершиной текущего узла и вернуться к шагу 1.

Шаг 7 . Если у текущего узла существует правая вершина, то сделать ее текущим узлом и вернуться к шагу 3, иначе перейти к шагу 8.

Шаг 8 . Создать новую вершину, поместить в нее очередной идентификатор, сделать эту новую вершину правой вершиной текущего узла и вернуться к шагу 1.

На рис.1 показана последовательность построения таблицы идентификаторов в форме бинарного дерева для входного потока идентификаторов: G D M E A B F . На рис.1,а показана таблица с одним корневым элементом для идентификатора G. Теперь надо записать идентификатор D. Для него выбирается левая ветвь от корня дерева, так как D G (рис.1,b). Далее запишем идентификатор M. Так как M > G , для M выбирается правая ветвь от узла G (рис.1, b ). Наконец, запишем идентификатор E. Так как E G, то идем по левой дуге от узла G и попадаем в узел D, E> D , поэтому E попадает в правую ветвь от узла D (рис.1,с). На рис.1, d изображено дерево после того, как в него были добавлены идентификаторы A, B и F.

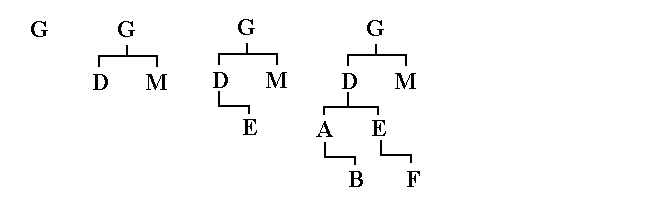Рис. 1. Пример таблицы идентификаторов в форме бинарного дерева

Поиск нужного элемента в таблице идентификаторов в форме бинарного дерева выполняется по алгоритму, схожему с алгоритмом XE «Алгоритм:поиска в бинарном дереве» заполнения этого дерева:

Шаг 1 . Сделать текущим узлом дерева корневую вершину.

Шаг 2 . Сравнить искомый идентификатор с идентификатором, содержащимся в текущем узле дерева.

Шаг 3 . Если идентификаторы совпадают, то искомый идентификатор найден, алгоритм поиска завершен, иначе надо перейти к шагу 4.

Шаг 4 . Если очередной идентификатор меньше, то перейти к шагу 5, иначе — перейти к шагу 6.

Шаг 5 . Если у текущего узла существует левая вершина, то сделать ее текущим узлом и вернуться к шагу 2, иначе искомый идентификатор не найден, алгоритм завершен.

Шаг 7 . Если у текущего узла существует правая вершина, то сделать ее текущим узлом и вернуться к шагу 2, иначе искомый идентификатор не найден, алгоритм завершен.

Например, произведем поиск в дереве, изображенном на рис. 1, идентификатора A . Берем корневую вершину G (она становится текущим узлом), сравниваем идентификаторы G и A . Искомый идентификатор меньше – текущим узлом становится левая вершина D . Опять сравниваем идентификаторы. Искомый идентификатор меньше – текущим узлом становится левая вершина A . При следующем сравнении искомый идентификатор найден.

Если искать отсутствующий в таблице идентификатор – например, A 11, то поиск опять пойдет от корневой вершины. Сравниваем идентификаторы G и A 11. Искомый идентификатор меньше – текущим узлом становится левая вершина D . Опять сравниваем идентификаторы. Искомый идентификатор меньше – текущим узлом становится левая вершина A . Снова выполняем сравнение. Искомый идентификатор больше – текущим узлом становится правая вершина B . Сравниваем A 11 и B . Искомый идентификатор меньше, но левая вершина у узла B отсутствует, поэтому в данном случае искомый идентификатор не найден.

Для данного метода количество требуемых сравнений и форма получившегося дерева зависят от порядка, в котором идентификаторы поступают на вход. В среднем при большом количестве идентификаторов можно считать, что метод бинарного дерева, как и метод бинарного поиска на каждом шаге сокращает количество искомых элементов в два раза. Тогда среднее время поиска идентификатора в дереве можно оценить как: T _п

1+[ log ₂ N ], где N – количество идентификаторов в таблице. Но поскольку запись нового идентификатора в дерево выполняется по аналогичному алгоритму и, в отличие от упорядоченного массива, не требует сдвига данных, среднее время записи нового идентификатора в дерево также можно оценить как: T _з

Как видно, среднестатистически метод организации таблицы идентификаторов в форме бинарного дерева имеет лучшие характеристики, чем метод, основанный на упорядоченном линейном списке за счёт отсутствия необходимости сдвигать уже существующие элементы таблицы при добавлении нового идентификатора. Однако метод, основанный на бинарном дереве, имеет два основных недостатка.

Первый его недостаток связан с самой формой организации таблицы – деревом. Для размещения бинарного дерева в памяти компьютера потребуются накладные расходы вычислительных ресурсов, вызванные необходимостью работы с динамической памятью при размещении элементов дерева, а также необходимостью хранения двух ссылок на дочерние элементы в каждом элементе таблицы. Этот недостаток можно считать несущественным.

Второй недостаток данного метода связан с тем, что форма дерева, а значит, и эффективность метода существенно зависят от порядка поступления идентификаторов на вход. В частности, если идентификаторы поступают на вход упорядоченно (в прямом или обратном алфавитном порядке – например, A B C C 22 D 1), построенное дерево получается полностью вырожденным в одну единственную ветвь и эффективность метода теряется. Но в реальных компьютерных программах идентификаторы поступают на вход неупорядоченно, поэтому данным недостатком можно пренебречь.

Таким образом, с учётом условий применения для ренальных входных программ метод построения таблицы идентификаторов в форме бинарного дерева достаточно эффективен. Данный метод применялся в реальных компиляторах.

Хеш-функции и хеш-адресация

Принципы работы хеш-функций

Логарифмическая зависимость времени поиска и времени заполнения таблицы идентификаторов от количества идентификаторов – это самый лучший результат, которого можно достичь за счет применения простейших методов организации таблиц. Однако в реальных исходных программах количество идентификаторов столь велико (десятки тысяч и более), что даже логарифмическую зависимость времени поиска от их числа нельзя признать удовлетворительной. Необходимы более эффективные методы поиска информации в таблице идентификаторов.

Лучших результатов можно достичь, если применить методы, связанные с использованием хеш-функций и хеш-адресации.

Хеш-функцией F называется некоторое отображение множества входных элементов R на множество целых неотрицательных чисел Z : F ( r ) = n , r Î R , n Î Z . Сам термин «хеш-функция» происходит от английского термина « hash function » ( hash — «мешать», «смешивать», «путать»). Множество допустимых входных элементов R называется областью определения хеш-функции. Множеством значений хеш-функции F называется подмножество M из множества целых неотрицательных чисел Z : M Í Z , содержащее все возможные значения, возвращаемые функцией F : » r Î R : F ( r ) Î M и » m Î M : $ r Î R : F ( r )= m . Процесс отображения области определения хеш-функции на множество значений называется «хешированием».

При работе с таблицей идентификаторов хеш-функция должна выполнять отображение имен идентификаторов на множество целых неотрицательных чисел. Областью определения такой хеш-функции будет множество всех возможных имен идентификаторов.

Хеш-адресация заключается в использовании значения, возвращаемого хеш-функцией, в качестве адреса ячейки некоторого массива данных. Размер массива должен соответствовать области значений используемой хеш-функции. В реальном компиляторе область значений хеш-функции не должна превышать размер доступного адресного пространства компьютера.

Метод организации таблиц идентификаторов, основанный на использовании хеш-адресации, заключается в размещении каждого элемента таблицы в ячейке, адрес которой возвращает хеш-функция, вычисленная для этого элемента. Тогда в идеальном случае для размещения любого элемента в таблице идентификаторов достаточно вычислить его хеш-функцию и обратиться к нужной ячейке массива данных. Для поиска элемента в таблице необходимо вычислить хеш-функцию для искомого элемента и проверить, не является ли заданная ею ячейка массива пустой. Если она не пуста – элемент найден, если пуста – не найден. Первоначально все ячейки массива данных должны быть пустыми.

Этот метод весьма эффективен, поскольку как время размещения элемента в таблице, так и время его поиска определяются только временем, затрачиваемым на вычисление хеш-функции, которое в общем случае несопоставимо меньше времени, необходимого на многократные сравнения элементов таблицы.

Метод имеет два очевидных недостатка. Первый из них – неэффективное использование объема памяти под таблицу идентификаторов: размер массива для ее хранения должен соответствовать области значений хеш-функции, в то время как реально хранимых в таблице идентификаторов может быть существенно меньше. Второй недостаток – необходимость соответствующего разумного выбора хеш-функции.

Построение таблиц идентификаторов на основе хеш-функций

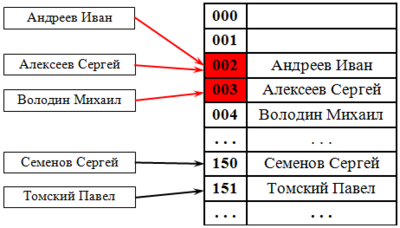
Существуют различные варианты хеш-функций. Получение результата хеш-функции – «хеширование» – обычно достигается за счет выполнения над цепочкой символов некоторых простых арифметических и/или логических операций. Самой простой хеш-функцией для символа является код внутреннего представления в компьютере литеры символа. Эту хеш-функцию можно использовать и для цепочки символов, выбирая первый ее символ. Например, если двоичное представление символа А есть код 00100001₂ , то результатом хеширования идентификатора ATable будет код 00100001₂ .

Хеш-функция, предложенная выше, очевидно не удовлетворительна: при использовании такой хеш-функции возникнет проблема – двум различным идентификаторам, начинающимся с одной и той же буквы, будет соответствовать одно и то же значение хеш-функции. Тогда при хеш-адресации в одну ячейку таблицы идентификаторов по одному и тому же адресу должны быть помещены два различных идентификатора, что явно невозможно. Ситуация, когда двум или более идентификаторам соответствует одно и то же значение хеш-функции, называется коллизией.

Естественно, что хеш-функция, допускающая коллизии, не может быть напрямую использована для хеш-адресации в таблице идентификаторов. Достаточно получить хотя бы один случай коллизии на всем множестве идентификаторов, чтобы такой хеш-функцией нельзя было пользоваться непосредственно. Но в примере взята самая элементарная хеш-функция. А возможно ли построить хеш-функцию, которая бы полностью исключала возникновение коллизий?

Для полного исключения коллизий хеш-функция должна быть взаимно однозначной: каждому элементу из области определения хеш-функции должно соответствовать одно значение из ее множества значений, и каждому значению из множества значений этой функции должен соответствовать только один элемент из ее области определения. Тогда двум произвольным элементам из области определения хеш-функции будут всегда соответствовать два различных ее значения. Теоретически для идентификаторов такую хеш-функцию построить можно, так как и ее область определения (все возможные имена идентификаторов), и область ее значений (целые неотрицательные числа) являются бесконечными счетными множествами. Теоретически можно организовать взаимно однозначное отображение одного счетного множества на другое.

Но на практике существует ограничение, делающее создание взаимно однозначной хеш-функции для идентификаторов невозможным. Дело в том, что в реальности область значений любой хеш-функции ограничена размером доступного адресного пространства компьютера. При организации хеш-адресации значение, используемое в качестве адреса таблицы идентификаторов, не может выходить за пределы, заданные разрядностью адреса компьютера. Множество адресов любого компьютера может быть велико, но оно всегда конечно, то есть ограничено. Организовать взаимно однозначное отображение бесконечного счётного множества на конечное даже теоретически невозможно. Можно учесть, что длина принимаемой во внимание части имени идентификатора в реальных компиляторах также ограничена – обычно она лежит в пределах от 32 до 128 символов (то есть, и область определения хеш-функции конечна). Но и тогда количество элементов в конечном множестве, составляющем область определения функции, будет превышать их количество в области значений функции (количество всех возможных идентификаторов больше количества допустимых адресов в современных компьютерах). Таким образом, создать взаимно однозначную хеш-функцию практически невозможно. Следовательно, невозможно избежать возникновения коллизий.

Поэтому на практике хеш-адресацию используют не напрямую, а в сочетании с каким-либо методом, позволяющим бороться с возникающими коллизиями. Часть таких методов рассмотрена далее.

Построение таблиц идентификаторов с помощью рехеширования

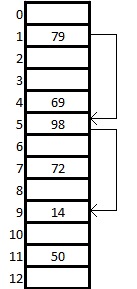
Для решения проблемы коллизии можно использовать много способов. Одним из них является метод рехеширования (или расстановки). Согласно этому методу, если для элемента A адрес h ( A ), вычисленный с помощью хеш-функции h , указывает на уже занятую ячейку, то необходимо вычислить значение функции n ₁= h ₁( A ) и проверить занятость ячейки по адресу n ₁. Если и она занята, то вычисляется значение h ₂( A ) и так до тех пор, пока либо не будет найдена свободная ячейка, либо очередное значение h_i ( A ) совпадет с h ( A ). В последнем случае считается, что таблица идентификаторов заполнена, и места в ней больше нет – тогда выдается информация об ошибке размещения идентификатора в таблице.

Такую таблицу идентификаторов можно организовать по следующему алгоритму размещения элемента:

Шаг 1: Вычислить значение хеш-функции n = h ( A ) для нового элемента A .

Шаг 2: Если ячейка по адресу n пустая, то поместить в нее элемент A и завершить алгоритм, иначе i :=1 и перейти к шагу 3.

Шаг 3: Вычислить n_i = h_i ( A ). Если ячейка по адресу n_i пустая, то поместить в нее элемент A и завершить алгоритм, иначе перейти к шагу 4.

Шаг 4: Если n = n_i , то сообщить об ошибке и завершить алгоритм, иначе i := i +1 и вернуться к шагу 3.

Поиск элемента A в таблице идентификаторов, организованной таким образом, будет выполняться по следующему алгоритму:

Шаг 1: Вычислить значение хеш-функции n = h ( A ) для искомого элемента A .

Шаг 2: Если ячейка по адресу n пустая, то элемент не найден, алгоритм завершен, иначе сравнить имя элемента в ячейке n с именем искомого элемента A . Если они совпадают, то элемент найден и алгоритм завершен, иначе i :=1 и перейти к шагу 3.

Шаг 3: Вычислить n_i = h_i ( A ). Если ячейка по адресу n_i пустая или n = n_i , то элемент не найден и алгоритм завершен, иначе сравнить имя элемента в ячейке n_i с именем искомого элемента A . Если они совпадают, то элемент найден и алгоритм завершен, иначе i := i +1 и повторить шаг 3.

При такой организации таблиц идентификаторов в случае возникновения коллизии алгоритм размещает элементы в пустых ячейках таблицы, выбирая их определенным образом. При этом элементы могут попадать в ячейки с адресами, которые потом будут совпадать со значениями хеш-функции, что приведет к возникновению новых, дополнительных коллизий. Таким образом, количество операций, необходимых для поиска или размещения в таблице элемента, зависит от заполненности таблицы.

Для организации таблицы идентификаторов по методу рехеширования необходимо определить все хеш-функции h_i для всех i . Чаще всего функции h_i определяют как некоторую модификацию хеш-функции h . Например, самым простым методом вычисления функции h_i(A) является ее организация в виде h_i(A) = (h(A) + p_i) mod N_m, где p_i — некоторое вычисляемое целое число, а N_m – максимальное значение из области значений хеш-функции h . В свою очередь, самым простым подходом здесь будет положить p_i = i . Тогда получаем формулу h_i ( A ) = ( h ( A )+ i ) mod N_m . В этом случае при совпадении значений хеш-функции для каких-либо элементов поиск свободной ячейки в таблице начинается последовательно от текущей позиции, заданной хеш-функцией h ( A ). Такой метод называется простым рехешированием.

Этот способ нельзя признать особенно удачным — при совпадении хеш-адресов элементы в таблице начинают группироваться вокруг них, что увеличивает число необходимых сравнений при поиске и размещении. Но даже такой примитивный метод рехеширования является достаточно эффективным средством организации таблицы идентификаторов при неполном ее заполнении.

Среднее время на помещение одного элемента в таблицу и на поиск элемента в таблице можно снизить, если применить более совершенный метод рехеширования. Одним из таких методов является использование в качестве p_i для функции h_i ( A )=( h ( A )+ p_i ) mod N_m последовательности псевдослучайных целых чисел p ₁, p ₂, …, p_k . При хорошем выборе генератора псевдослучайных чисел длина последовательности k будет k = N_m . В качестве самого простого варианта последовательности псевдослучайных чисел можно взять вычисление p_i по формуле p_i =( i * K )/ L , где K и L должны быть простыми числами ( L выбирают максимально близко к N_m , а K берут около L /2).

Существуют и другие методы организации функций рехеширования h_i ( A ), основанные на квадратичных вычислениях или, например, на вычислении по формуле: h_i ( A ) = ( h ( A )* i ) mod N_m , если N_m – простое число. В целом рехеширование позволяет добиться неплохих результатов для эффективного поиска элемента в таблице (лучших, чем бинарный поиск и бинарное дерево), но эффективность метода сильно зависит от заполненности таблицы идентификаторов и качества используемой хеш-функции – чем реже возникают коллизии, тем выше эффективность метода. Как показывают расчёты, при выборе качественной хеш-функции (например, хеширование по алгоритмам MD 5 или MD 6) метод простого рехеширования является более эффективным, чем бинарный поиск или бинарное дерево при заполненности таблицы идентификаторов до 80%. Требование неполного заполнения таблицы ведет к неэффективному использованию объема доступной памяти.

Несмотря на указанные недостатки, метод организации таблицы идентификаторов на основе рехеширования имеет практическое применение и встречается в реализациях реальных компиляторов.

Построение таблиц идентификаторов по методу цепочек

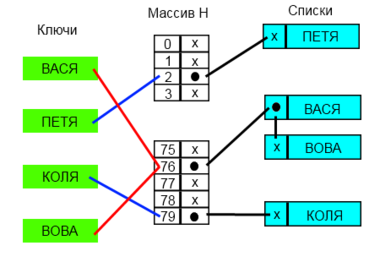
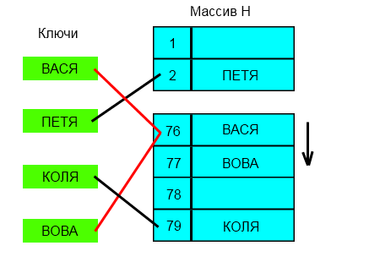
Неполное заполнение таблицы идентификаторов при применении хеш-функций ведет к неэффективному использованию всего объема памяти, доступного компилятору. Причем объем неиспользуемой памяти будет тем выше, чем больше информации хранится для каждого идентификатора. Этого недостатка можно избежать, если дополнить таблицу идентификаторов некоторой промежуточной хеш-таблицей.

В ячейках хеш-таблицы может храниться либо пустое значение, либо значение указателя на некоторую область памяти из основной таблицы идентификаторов. Тогда хеш-функция вычисляет адрес, по которому происходит обращение сначала к хеш-таблице, а потом уже через нее по найденному адресу – к самой таблице идентификаторов. Если соответствующая ячейка таблицы идентификаторов пуста, то ячейка хеш-таблицы будет содержать пустое значение. Тогда вовсе не обязательно иметь в самой таблице идентификаторов ячейку для каждого возможного значения хеш-функции – таблицу можно сделать динамической так, чтобы ее объем рос по мере заполнения.

Такой подход позволяет добиться двух положительных результатов: во-первых, нет необходимости заполнять пустыми значениями таблицу идентификаторов – это можно сделать только для хеш-таблицы; во-вторых, каждому идентификатору будет соответствовать строго одна ячейка в таблице идентификаторов (в ней не будет пустых неиспользуемых ячеек). Пустые ячейки будут только в хеш-таблице, и объем неиспользуемой памяти не будет зависеть от объема информации, хранимой для каждого идентификатора – для каждого значения хеш-функции будет расходоваться только память, необходимая для хранения одного указателя.

На основе этой схемы можно реализовать еще один способ организации таблиц идентификаторов с помощью хеш-функций, называемый « метод цепочек». Для метода цепочек в таблице идентификаторов к каждому элементу добавляется еще одно поле, в котором может содержаться ссылка на любой элемент таблицы. Первоначально это поле всегда пустое (никуда не указывает). Также для этого метода необходимо иметь одну специальную переменную, которая всегда указывает на первую свободную ячейку основной таблицы идентификаторов (первоначально – указывает на начало таблицы).

Метод цепочек работает следующим образом по следующему алгоритму:

Шаг 1: Во все ячейки хеш-таблицы поместить пустое значение, таблица идентификаторов пуста, переменная FreePtr (указатель первой свободной ячейки) указывает на начало таблицы идентификаторов; i :=1.

Шаг 2: Вычислить значение хеш-функции n_i для нового элемента A_i . Если ячейка хеш-таблицы по адресу n_i пустая, то поместить в нее значение переменной FreePtr и перейти к шагу 5; иначе перейти к шагу 3.

Шаг 3: Выбрать из хеш-таблицы адрес ячейки таблицы идентификаторов m и перейти к шагу 4.

Шаг 4: Для ячейки таблицы идентификаторов по адресу m проверить значение поля ссылки. Если оно пустое, то записать в него адрес из переменной FreePtr и перейти к шагу 5; иначе выбрать из поля ссылки адрес m и повторить шаг 4.

Шаг 5: Добавить в таблицу идентификаторов новую ячейку, записать в нее информацию для элемента A_i (поле ссылки должно быть пустым), в переменную FreePtr поместить адрес за концом добавленной ячейки. Если больше нет идентификаторов, которые надо разместить в таблице, то выполнение алгоритма закончено, иначе i := i +1 и перейти к шагу 2.

Поиск элемента в таблице идентификаторов, организованной таким образом, будет выполняться по следующему алгоритму:

Шаг 1: Вычислить значение хеш-функции n для искомого элемента A . Если ячейка хеш-таблицы по адресу n пустая, то элемент не найден и алгоритм завершен, иначе выбрать из хеш-таблицы адрес ячейки таблицы идентификаторов m .

Шаг 2: Сравнить имя элемента в ячейке таблицы идентификаторов по адресу m с именем искомого элемента A . Если они совпадают, то искомый элемент найден и алгоритм завершен, иначе перейти к шагу 3.

Шаг 3: Проверить значение поля ссылки в ячейке таблицы идентификаторов по адресу m . Если оно пустое, то искомый элемент не найден и алгоритм завершен; иначе выбрать из поля ссылки адрес m и перейти к шагу 2.

При такой организации таблиц идентификаторов в случае возникновения коллизии алгоритм размещает элементы в ячейках таблицы, связывая их друг с другом последовательно через поле ссылки. При этом элементы не могут попадать в ячейки с адресами, которые потом будут совпадать со значениями хеш-функции. Таким образом, дополнительные коллизии не возникают. В итоге в таблице возникают своеобразные цепочки связанных элементов, откуда происходит и название данного метода – «метод цепочек».

Метод цепочек является очень эффективным средством организации таблиц идентификаторов. Среднее время на размещение одного элемента и на поиск элемента в таблице для него зависит только от среднего числа коллизий, возникающих при вычислении хеш-функции. Накладные расходы памяти, связанные с необходимостью иметь одно дополнительное поле указателя в таблице идентификаторов на каждый ее элемент, можно признать вполне оправданными. Этот метод позволяет более экономно использовать память, чем метод, основанный на рехешировании, но при этом требует организации работы с динамическими массивами данных. Поэтому метод цепочек сложнее в реализации, чем метод рехеширования.

Метод цепочек находит практическое применение в реальных компиляторах наряду с методом рехеширования. Какой из методов организации таблиц идентификаторов использовать в каждом конкретном случае решают разработчики компилятора.

Комбинированные способы построения таблиц идентификаторов

Выше в примере была рассмотрена весьма примитивная хеш-функция, которую никак нельзя назвать удовлетворительной. Хорошая хеш-функция распределяет поступающие на ее вход идентификаторы равномерно на все имеющиеся в распоряжении адреса, так что коллизии возникают не столь часто. Существует большое множество хеш-функций. Каждая из них стремится распределить адреса под идентификаторы по своему алгоритму, но, как было показано выше, идеального хеширования достичь невозможно.

То, какой конкретно метод применяется в компиляторе для организации таблиц идентификаторов, зависит от реализации компилятора. Один и тот же компилятор может иметь даже несколько разных таблиц идентификаторов, организованных на основе различных методов.

Как правило, применяются комбинированные методы. В этом случае, как и для метода цепочек, в таблице идентификаторов организуется специальное дополнительное поле ссылки. Но в отличие от метода цепочек оно имеет несколько иное значение. При отсутствии коллизий для выборки информации из таблицы используется хеш-функция, поле ссылки остается пустым. Если же возникает коллизия, то через поле ссылки организуется поиск идентификаторов, для которых значения хеш-функции совпадают по одному из рассмотренных выше методов: неупорядоченный список, упорядоченный список или же бинарное дерево. При хорошо построенной хеш-функции коллизии будут возникать редко, поэтому количество идентификаторов, для которых значения хеш-функции совпали, будет не столь велико. Тогда и время поиска одного среди них будет незначительным (в принципе, при высоком качестве хеш-функции подойдет даже перебор по неупорядоченному списку).

Такой подход имеет преимущество по сравнению с методом цепочек, поскольку не требует использования промежуточной хеш-таблицы. Недостатком метода является необходимость работы с динамически распределяемыми областями памяти. Эффективность такого метода, очевидно, в первую очередь зависит от качества применяемой хеш-функции, а во вторую — от метода организации дополнительных хранилищ данных.

Хеш-адресация – это метод, который применяется не только для организации таблиц идентификаторов в компиляторах. Данный метод нашел свое применение и в операционных системах, и в системах управления базами данных.

Порядок выполнения работы

1. Получить вариант задания у преподавателя.

2. Разработать алгоритм организации таблицы идентификаторов в соответствии с заданием.

3. Подготовить и защитить отчет.

4. Написать и отладить программу на ЭВМ.

5. Сдать работающую программу преподавателю.

Требования к оформлению отчета

Отчет по лабораторной работе должен содержать следующие разделы:

· Краткое изложение цели работы.

· Задание по лабораторной работе с описанием своего варианта.

· Схему организации хеш-таблицы (в соответствии с вариантом задания).

· Описание алгоритма поиска в хеш-таблице (в соответствии с вариантом задания).

· Выводы по проделанной работе.

Основные контрольные вопросы

1. Что такое таблица символов (таблица идентификаторов) и для чего она предназначена?

2. Какая информация может храниться в таблице символов?

3. Какие операции выполняет компилятор с таблицей символов? В чем особенность работы компилятора с этой таблицей?

4. Какие цели преследуются при организации таблицы символов?

5. Какими характеристиками могут обладать идентификаторы (именованные константы, переменные)?

6. Какие существуют простейшие способы организации таблиц символов?

7. В чем заключается алгоритм логарифмического поиска? Какие преимущества он дает по сравнению с простым перебором и какие он имеет недостатки?

8. Расскажите о древовидной организации таблиц идентификаторов. В чем ее преимущества и недостатки?

9. Что такое хеш-функции и для чего они используются?

10. В чем суть хеш-адресации?

11. Расскажите о преимуществах и недостатках организации таблицы идентификаторов с помощью хеш-функции.

12. Что такое коллизия? Почему она происходит? Можно ли полностью избежать коллизий?

13. Что такое рехеширование? Какие методы рехеширования существуют?

14. В чем заключается метод цепочек?

15. Сравните между собой методы организации таблицы идентификаторов на основе рехеширования и с помощью метода цепочек.

16. Как могут быть скомбинированы различные методы организации хеш-таблиц?

Варианты заданий

Для выполнения лабораторной работы требуется написать программу, которая получает на входе набор идентификаторов, организует таблицу по заданному методу и позволяет осуществить многократный поиск идентификатора в этой таблице. Список идентификаторов считать заданным в виде текстового файла. Длину идентификаторов можно считать ограниченной 32 символами.

Для организации таблицы используется простейшая хэш-функция, указанная в варианте задания, а при возникновении коллизий используется дополнительный метод размещения идентификаторов в памяти. Если в качестве этого метода используется дерево или список, то они должны быть связаны с элементом главной хэш-таблицы.

В каждом варианте требуется, чтобы программа сообщала среднее число коллизий и среднее количество сравнений, выполненных для поиска идентификатора. Варианты заданий приведены далее в таблице 1.

Варианты заданий для лабораторной работы №1

Источник