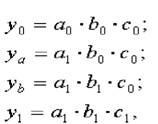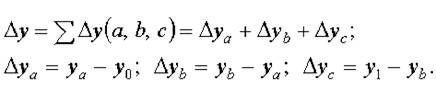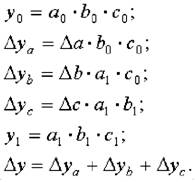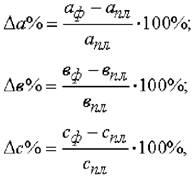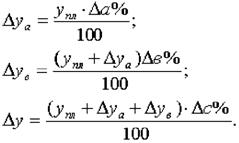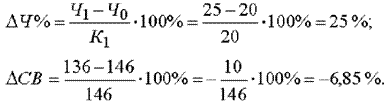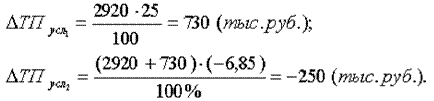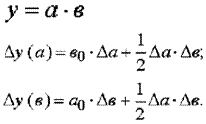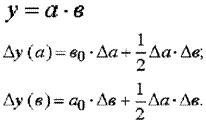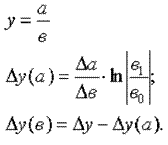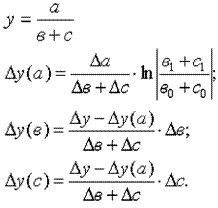Способ разниц или цепной подстановки

Метод цепных подстановок и абсолютных разниц

Метод цепных подстановок является одним из базовых методов экономического анализа, который применяется для анализа мультипликативных моделей. При этом каждый фактор последовательно изменяется с базисного на отчетное значение, тогда как остальные остаются без изменения.

Можно проводить расчеты в таблице. Предположим, что анализируемый показатель «А» представляет собой произведение трех факторов (Ф1, Ф2, Ф3).

Абсолютное изменение показателя известно. Необходимо определить суммы факторного влияния – насколько изменился результирующий показатель под влиянием изменения конкретного фактора. Размер факторного влияния Аф1, Аф2, Аф3 будет определяться следующим образом:

Фактор 1	Фактор 2	Фактор 3	Анализируемый показатель	Размер влияния на анализируемый показатель
Базисный	Базисный	Базисный	Базисный (Б)
Отчетный	Базисный	Базисный	Условный 1 (У1)	Аф1 = У 1 – Б
Отчетный	Отчетный	Базисный	Условный 2 (У2)	Аф2 = У 2 – У 1
Отчетный	Отчетный	Отчетный	Отчетный (О)	Аф3 = О – У 2

Общая сумма факторных отклонений дает абсолютное отклонение (изменение) показателя. Достоинством приема является то, что количество факторов не имеет значения и не влияет на методику расчета, увеличивается только количество «шагов» расчета.

Для примера представим выручку условного транспортного предприятия как произведение следующих факторов – количество машин, количество рейсов одной машины, количество пассажиров за одну поездку и стоимость проезда одного пассажира:

Данные о значении факторов в базисном и отчетном периоде представлены в таблице 7.

Показатель	Обозначение	Базисный период	Отчетный период
Количество машин	М
Количество рейсов	Р
Количество пассажиров	П
Стоимость проезда	С
Выручка	В

Абсолютное отклонение выручки составит + 180000 р.

Рассчитаем факторные отклонения. Если все факторы будут иметь базисное значение, сумма выручки составляет 1500000 р.

Затем мы будем постепенно заменять значения факторов с базисного значения на отчетное:

В базис = 25*10*40*150 =1500000

В усл 1 = 30*10*40*150 = 1800000

1440000 – 1800000 = — 360000.

В усл 2 = 30*8*40*150 = 1440000

1260000 – 1440000 = — 180000.

В усл 3 = 30*8*35*150 = 1260000

1680000 – 1260000 = + 420000.

В отчет = 30*8*35*200 = 1680000

По итогам расчетов можно сделать вывод, что за счет увеличения количества машин предприятие получило дополнительную выручку в сумме 300000 рублей, а за счет увеличения тарифа – в сумме 420000 рублей. В то же время сказалось отрицательное влияние таких факторов, как уменьшение количества рейсов одной машины и уменьшение количества пассажиров на каждом рейсе (недополучено выручки на сумму360000 и 180000 рублей соответственно).

Прием цепных подстановок считается основным приемом факторного анализа, но имеет существенный недостаток – наличие так называемого «неразложимого остатка». Это означает, что при изменении порядка факторов в модели изменяется сумма факторных отклонений. Поэтому при составлении моделей для проведения факторного анализа существует следующее правило – сначала указываются количественные, а затем стоимостные показатели. Если необходимо обеспечить высокую точность расчетов, используются логарифмический или интегральный прием.

Метод абсолютных разниц является разновидностью приема цепных подстановок. Каждый фактор последовательно представляется в виде разницы между отчетным и базисным значениями. Остальные показатели принимаются в отчетном или базисном значении в зависимости от расположения в формуле (соответственно до анализируемого фактора или после него).

Аф1 = (Ф1о – Ф1б) * Ф2б * Ф3б;

Аф2 = Ф1о * (Ф2о – Ф2б) * Ф3б;

Аф3 = Ф1о * Ф2о * (Ф3о-Ф3б),

где Ф1б, Ф2б, Ф3б – факторы в своем базисном значении;

Ф1о, Ф2о, Ф3о – факторы в своем отчетном значении.

Вопросы для обсуждения:

1. Почему метод абсолютных разниц считается разновидностью метода цепных подстановок? Какой из предложенных приемов факторного анализа проще применять и почему?

2. Можно ли представить модель, предложенную в примере, как произведение большего количества факторов? Как произведение меньшего количества факторов?

Задачи и ситуации:

1. Рассчитать показатели рентабельности продукции и капитала по данным условного предприятия и определить, используя формулу Дюпона, влияние на изменение рентабельности активов изменения рентабельности продукции и оборачиваемости активов. Аналогичные расчеты провести по рентабельности собственного капитала.

Показатель	Прошлый год	Отчетный год
Выручка
Валюта баланса
Прибыль до налогообложения
Собственный капитал

2. Рассчитать при помощи приема абсолютных разниц:

Влияние на суммарные материальные затраты изменений в стоимости сырья и нормы расхода сырья на производство продукции.

Показатели	Прошлый год	Отчетный год
Стоимость 1 кг сырья
Норма расхода, кг
Материальные затраты	?	?

Определить разницу в значении факторных отклонений при изменении места расположения показателей — факторов.

3. Составить мультипликативную модель и определить факторное влияние на изменение товарооборота следующих факторов:

— средняя стоимость товара;

— количество работников торгового зала;

— количество проданных товаров на одного работника.

Источник

Метод цепных подстановок

Способ цепных подстановок может быть использован во всех типах детерминированных факторных моделей (аддитивные, мультипликативные, кратные, комбинированные) для расчёта величины влияния фактора на результат.

Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью рассчитывают ряд условных величин, которые учитывают изменение одного, двух и т.д. факторов, допуская, что остальные факторы не меняются. Сравнение величины результата до и после изменения уровня того или иного фактора позволяют элиминироваться от влияний всех факторов, кроме одного.

Алгоритм метода цепных подстановок для многофакторной мультипликативной модели

1. Рассчитываем плановый показатель: Y0 = a0 * b0 * с0* d0;

2. Далее рассчитывается система условных показателей:
Y_усл.1 = a1 * b0 * с0* d0;
Y_усл.2 = a1 * b1 * с0* d0;
Y_усл.3 = a1 * b1 * с1* d0;

3. Рассчитываем фактический показатель: Y1 = a1 * b1 * с1* d1;

4. Путем последовательного вычитания полученных показателей находим изменение результативного показателя за счет факторов:
ΔYа = Y_усл.1 – Y0;
ΔYb = Y_усл.2 – Y_усл.1;
ΔYс = Y_усл.3 – Y_усл.2;
ΔYd = Y1– Y_усл.3;
5. Рассчитываем общее отклонение фактического показателя от планового, которое равно сумме факторных отклонений:
ΔY = Y1 — Y0 = ΔYа + ΔYb + ΔYс + ΔYd

Рекомендации при использовании этого метода:
А) в первую очередь учитываются изменения количественных показателей, затем качественные;
Б) сначала учитываются факторы первого уровня подчинения, затем второго и т.д.

Пример . Исходные данные для расчета влияния факторов базисные: (y0 = 1,58; a0 = 12940; b0 = 8210 ) и фактические: (y1 = 1,53; a1 = 13950; b1 = 9124; ). Рассчитайте влияние на отклонение результативного показателя (y) каждого из определяющих его факторов (a, b).

Источник

Тема 4. Метод детерменированного факторного анализа

4.1. Метод цепных подстановок

Метод цепных подстановок заключается в определении ряда промежуточных значений результативного показателя путем последовательной замены базисных значений факторов на отчетные. Данный способ основан на элиминировании. Элиминировать — значит устранить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Предполагается, что все факторы изменяются независимо друг от друга, т.е. сначала изменяется один фактор, а все остальные остаются без изменения, потом изменяются два при неизменности остальных и т.д.

В общем виде применение способа цепных постановок можно описать следующим образом:

где a₀, b₀, c₀ — базисные значения факторов, оказывающих влияние на обобщающий показатель у;
a₁ , b₁, c₁ — фактические значения факторов;
y_a, y_b, — промежуточные изменения результирующего показателя, связанного с изменением факторов а, b соответственно.

Общее изменение Δу = у₁ — у₀ складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов:

Рассмотрим пример. Исходные данные для факторного анализа сведены в таблицу 4.1. На основе этих данных проведем описанным выше способом анализ влияния на объем товарной продукции количества работников и их выработки.

Исходные данные для факторного анализа

Показатели	Услов. обозн-я	Базисные значения (0)	Фактические значения (1)	Изменение
				Абсолютное (+,- )	Относительное (%)
Объем товарной продукции, тыс. руб.	ТП	2920	3400	+480	116,40
Количество работников, чел	Ч	20	25	+5	125,00
Выработка на одного работающего, тыс. руб.	СВ	146	136	-10	93,15

Зависимость объема товарной продукции от данных факторов можно описать с помощью мультипликативной модели:

Тогда влияние изменения величины количества работников на обобщающий показатель можно рассчитать по формуле:

Далее определим влияние изменения выработки работников на обобщающий показатель:

Таким образом, на увеличение объема товарной продукции на 730 тыс. руб. положительное влияние оказало изменение на 5 человек численности работников. Отрицательное влияние оказало снижение выработки на 10 тыс. руб., что вызвало снижение объема на 250 тыс. руб. Суммарное влияние двух факторов привело к увеличению объема продукции на 480 тыс. руб.

Преимущества данного способа: универсальность применения, простота расчетов.

Недостаток метода состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения. Это связано с тем, что в результате применения этого метода образуется некий неразложимый остаток, который прибавляется к величине влияния последнего фактора. На практике точностью оценки факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора. Однако существуют определенные правила, определяющие последовательность подстановки:

• при наличии в факторной модели количественных и качественных показателей в первую очередь рассматривается изменение количественных факторов;
• если модель представлена несколькими количественными и качественными показателями, то в первую очередь определяется влияние факторов первого порядка, затем второго и т.д.

Под количественным факторами при анализе понимают те, которые выражают количественную определенность явлений и могут быть получены путем непосредственного учета (количество рабочих, станков, сырья и т.д.).

Качественные факторы определяют внутренние качества, признаки и особенности изучаемых явлений (производительность труда, качество продукции, средняя продолжительность рабочего дня и т.д.).

4.2. Метод абсолютных разниц

Метод абсолютных разниц является модификацией способа цепной подстановки. Изменение результативного показателя за счет каждого фактора определяется как произведение абсолютного прироста исследуемого фактора на базисную величину факторов, которые находятся справа от него и отчетную величину факторов, расположенных слева от него в модели.

4.3. Метод относительных разниц

Метод относительных разниц также является одной из модификацией способа цепной подстановки. Применяется для измерения влияния факторов на прирост результативного показателя в мультипликативных моделях. Он используется в случаях, когда исходные данные содержат определенные ранее относительные отклонения факторных показателей в процентах.

Для мультипликативных моделей типа у = а · в · с методика анализа следующая:

находят относительное отклонение каждого факторного показателя:

определяют отклонение результативного показателя у за счет каждого фактора

Пример. Воспользовавшись данными табл. 1, проведем анализ способом относительных разниц. Относительные отклонения рассматриваемых факторов составят:

Рассчитаем влияние на объем товарной продукции каждого фактора:

Результаты расчетов те же, что и при использовании предыдущего способа.

4.4. Интегральный метод

Интегральный метод применим к мультипликативным, кратным и смешанным моделям. Метод позволяет получать более точные результаты расчета влияния факторов по сравнению с методами цепной подстановки, абсолютных и относительных разниц. Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер, т. е. можно использовать также уже сформированные рабочие формулы, приводимые в специальной литературе:

4.5. Метод логарифмирования

Метод логарифмирования применяется для измерения влияния факторов только в мультипликативных моделях. Данный метод обеспечивает высокую точность расчетов. При этом результаты не зависят от местоположения факторов в модели. Дополнительный прирост от взаимодействия факторовраспределяется пропорционально доле изолированного влияния каждого фактора на уровень результативного показателя (пропорционально отношениям логарифмов факторных индексов к логарифму результативного показателя). При расчетах используются как натуральный, так и десятичный логарифм.

Рассмотрим возможность использования основных методов детерминированного анализа, обобщим вышеизложенное в виде матрицы (табл. 4.2).

Сферы применения способов детерминированного факторного анализа

Способы	Тип модели
	Мультипликативные	Аддитивные	Кратные	Смешанные
Цепной подстановки	+	+	+	+
Абсолютных разниц	+	—	+	—
Относительных разниц	+	—	—	у = а · (в — с)
Интегральный	+	—	+	у = a / Σвi
Логарифмический	+	—	—	—

Бальжинов А.В., Михеева Е.В. Анализ и диагностика финансово-хозяйственной деятельности предприятия: Учебн.пособ., — Улан-Удэ, 2003.

Источник