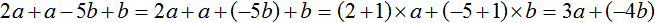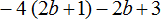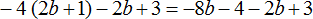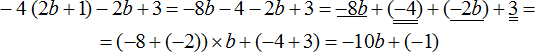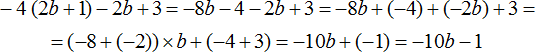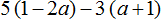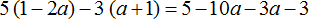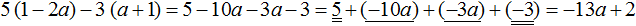Способ раскрытия скобок фонтанчиком

Раскрытие скобок

Продолжаем изучать основы алгебры. В данном уроке мы научимся раскрывать скобки в выражениях. Раскрыть скобки означает избавить выражение от этих скобок.

Чтобы раскрывать скобки, нужно выучить наизусть два правила. При регулярных занятиях раскрывать скобки можно с закрытыми глазами, и про те правила которые требовалось заучивать наизусть, можно благополучно забыть.

Первое правило раскрытия скобок

Рассмотрим следующее выражение:

Значение данного выражения равно 2. Раскроем скобки в данном выражении. Раскрыть скобки означает избавиться от них, не влияя на значение выражения. То есть после избавления от скобок значение выражения 8 + (−9 + 3) по прежнему должно быть равно двум.

Первое правило раскрытия скобок выглядит следующим образом:

При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.

Итак, мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Этот плюс нужно опустить вместе со скобками. Иными словами, скобки исчезнут вместе с плюсом, который перед ними стоял. А то, что было в скобках запишется без изменений:

Мы получили выражение без скобок 8−9+3 . Данное выражение равно 2, как и предыдущее выражение со скобками было равно 2.

Таким образом, между выражениями 8+(−9+3) и 8−9+3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

8 + (−9 + 3) = 8 − 9 + 3

Пример 2. Раскрыть скобки в выражении 3 + (−1 − 4)

Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках останется без изменений:

3 + (−1 − 4) = 3 − 1 − 4

Пример 3. Раскрыть скобки в выражении 2 + (−1)

Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках останется без изменений:

В данном примере раскрытие скобок стало своего рода обратной операцией замене вычитания сложением. Как это понимать?

В выражении 2 − 1 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 2 + (−1) . Но если в выражении 2 + (−1) раскрыть скобки, то получится изначальное 2 − 1 .

Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после каких-нибудь преобразований. То есть избавить его от скобок и сделать проще.

Чтобы упростить данное выражение, можно привести подобные слагаемые. Напомним, что для приведения подобных слагаемых, нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:

Получили выражение 3a + (−4b) . В этом выражении раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок, то есть опускаем скобки вместе с плюсом, который стоит перед этими скобками:

Таким образом, выражение 2a+a−5b+b упрощается до 3a−4b .

Раскрыв одни скобки, по пути могут встретиться другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в следующем выражении:

Здесь два места, где нужно раскрыть скобки. В данном случае применимо первое правило раскрытия скобок, а именно опускание скобок вместе с плюсом, который стоит перед этими скобками:

2 + (−3 + 1) + 3 + (−6) = 2 − 3 + 1 + 3 − 6

Пример 3. Раскрыть скобки в выражении 6+(−3)+(−2)

В обоих местах, где имеются скобки, перед ними стоит плюс. Здесь опять же применяется первое правило раскрытия скобок:

6 + (−3) + (−2) = 6 − 3 − 2

Иногда первое слагаемое в скобках записано без знака. Например, в выражении 1+(2+3−4) первое слагаемое в скобках 2 записано без знака. Возникает вопрос, а какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ напрашивается сам — перед двойкой будет стоять плюс.

На самом деле даже будучи в скобках перед двойкой стоит плюс, но мы его не видим по причине того, что его не записывают. Мы уже говорили, что полная запись положительных чисел выглядит как +1, +2, +3 . Но плюсы по традиции не записывают, поэтому мы и видим привычные для нас положительные числа 1, 2, 3 .

Поэтому, чтобы раскрыть скобки в выражении 1+(2+3−4) , нужно как обычно опустить скобки вместе с плюсом, стоящим перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:

1 + (2 + 3 − 4) = 1 + 2 + 3 − 4

Пример 4. Раскрыть скобки в выражении −5 + (2 − 3)

Перед скобками стоит плюс, поэтому применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед этими скобками. Но первое слагаемое, которое в скобках записываем со знаком плюс:

−5 + (2 − 3) = −5 + 2 − 3

Пример 5. Раскрыть скобки в выражении (−5)

Перед скобками стоит плюс, но он не записан по причине того, что до него не было других чисел или выражений. Наша задача убрать скобки, применив первое правило раскрытия скобок, а именно опустить скобки вместе с этим плюсом (даже если он невидим)

Пример 6. Раскрыть скобки в выражении 2a + (−6a + b)

Перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишется без изменений:

Пример 7. Раскрыть скобки в выражении 5a + (−7b + 6c) + 3a + (−2d)

В данном выражении имеется два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишется без изменений:

Второе правило раскрытия скобок

Теперь рассмотрим второе правило раскрытия скобок. Оно применяется тогда, когда перед скобками стоит минус.

Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный.

Например, раскроем скобки в следующем выражении

Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, стоящим перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:

Мы получили выражение без скобок 5 + 2 + 3 . Данное выражение равно 10, как и предыдущее выражение со скобками было равно 10.

Таким образом, между выражениями 5−(−2−3) и 5+2+3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

5 − (−2 − 3) = 5 + 2 + 3

Пример 2. Раскрыть скобки в выражении 6 − (−2 − 5)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок, а именно опускаем скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, записываем с противоположными знаками:

6 − (−2 − 5) = 6 + 2 + 5

Пример 3. Раскрыть скобки в выражении 2 − (7 + 3)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

2 − (7 + 3) = 2 − 7 − 3

Пример 4. Раскрыть скобки в выражении −(−3 + 4)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 5. Раскрыть скобки в выражении −(−8 − 2) + 16 + (−9 − 2)

Здесь два места, где нужно раскрыть скобки. В первом случае нужно применить второе правило раскрытия скобок, а когда очередь доходит до выражения +(−9 − 2) нужно применить первое правило:

−(−8 − 2) + 16 + (−9 − 2) = 8 + 2 + 16 − 9 − 2

Пример 6. Раскрыть скобки в выражении −(−a − 1)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 7. Раскрыть скобки в выражении −(4a + 3)

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 8. Раскрыть скобки в выражении a − (4b + 3) + 15

Перед скобками стоит минус, поэтому применяем второе правило раскрытия скобок:

Пример 9. Раскрыть скобки в выражении 2a + (3b − b) − (3c + 5)

Здесь два места, где нужно раскрыть скобки. В первом случае нужно применить первое правило раскрытия скобок, а когда очередь доходит до выражения −(3c+5) нужно применить второе правило:

2a + (3b − b) − (3c + 5) = 2a + 3b − b − 3c − 5

Пример 10. Раскрыть скобки в выражении −a − (−4a) + (−6b) − (−8c + 15)

Здесь три места, где нужно раскрыть скобки. Вначале нужно применить второе правило раскрытия скобок, затем первое, а затем опять второе:

−a − (−4a) + (−6b) − (−8c + 15) = −a + 4a − 6b + 8c − 15

Механизм раскрытия скобок

Правила раскрытия скобок, которые мы сейчас рассмотрели, основаны на распределительном законе умножения:

На самом деле раскрытием скобок называют ту процедуру, когда общий множитель умножают на каждое слагаемое в скобках. В результате такого умножения скобки исчезают. Например, раскроем скобки в выражении 3×(4+5)

3 × (4 + 5) = 3 × 4 + 3 × 5

Поэтому, если нужно умножить число на выражение в скобках (или выражение в скобках умножить на число) надо говорить раскроем скобки.

Но как связан распределительный закон умножения с правилами раскрытия скобок, которые мы рассматривали ранее?

Дело в том, что перед любыми скобками стоит общий множитель. В примере 3 × (4 + 5) общий множитель это 3 . А в примере a(b + c) общий множитель это переменная a .

Если перед скобками нет чисел или переменных, то общим множителем является 1 или −1 , в зависимости от того, какой знак стоит перед скобками. Если перед скобками стоит плюс, значит общим множителем является 1 . Если перед скобками стоит минус, значит общим множителем является −1 .

К примеру, раскроем скобки в выражении −(3b − 1) . Перед скобками стоит минус, поэтому нужно воспользоваться вторым правилом раскрытия скобок, то есть опустить скобки вместе с минусом, стоящим перед скобками. А выражение, которое было в скобках, записать с противоположными знаками:

Мы раскрыли скобки, воспользовавшись правилом раскрытия скобок. Но эти же скобки можно раскрыть, воспользовавшись распределительным законом умножения. Для этого сначала записываем перед скобками общий множитель 1, который не был записан:

Минус, который раньше стоял перед скобками относился к этой единице. Теперь можно раскрыть скобки, применяя распределительный закон умножения. Для этого общий множитель −1 нужно умножить на каждое слагаемое в скобках и полученные результаты сложить.

Для удобства заменим разность, находящуюся в скобках на сумму:

Далее умножаем общий множитель −1 на каждое слагаемое в скобках:

Как и в прошлый раз мы получили выражение −3b + 1 . Каждый согласится с тем, что в этот раз затрачено больше времени на решение столь простейшего примера. Поэтому разумнее пользоваться готовыми правилами раскрытия скобок, которые мы рассматривали в данном уроке:

Но не мешает знать, как эти правила работают.

В данном уроке мы научились ещё одному тождественному преобразованию. Вместе с раскрытием скобок, вынесением общего за скобки и приведением подобных слагаемых можно немного расширить круг решаемых задач. Например:

Раскрыть скобки и привести подобные слагаемые в следующем выражении:

Здесь нужно выполнить два действия — сначала раскрыть скобки, а потом привести подобные слагаемые. Итак, по порядку:

1) Раскрываем скобки:

2) Приводим подобные слагаемые:

В получившемся выражении −10b+(−1) можно раскрыть скобки:

Пример 2. Раскрыть скобки и привести подобные слагаемые в следующем выражении:

1) Раскроем скобки:

2) Приведем подобные слагаемые. В этот раз для экономии времени и места, не будем записывать, как коэффициенты умножаются на общую буквенную часть

Пример 3. Упростить выражение 8m+3m и найти его значение при m=−4

1) Сначала упростим выражение. Чтобы упростить выражение 8m+3m , можно вынести в нём общий множитель m за скобки:

2) Находим значение выражения m(8 + 3) при m = −4 . Для этого в выражение m(8 + 3) вместо переменной m подставляем число −4

m (8 + 3) = −4 (8 + 3) = −4 × 8 + (−4) × 3 = −32 + (−12) = −44

Источник

Алгебра

План урока:

Многочлен, вычисление значений многочлена

В предыдущем уроке мы познакомились с понятием одночлена. При записи одночленов не используется операция сложения. Если же возникает необходимость сложить несколько одночленов, то в результате получается многочлен.

В качестве примера многочленов можно привести следующие выражения:

Стоит обратить внимание, что в записи многочлена может использоваться и знак минус, при этом его всё равно можно считать суммой одночленов, а не разностью. Дело в том, что можно условно считать, что знак минус относится к коэффициенту одночлена, например:

Для некоторых видов многочленов существуют особые названия. Если многочлен состоит из двух одночленов, то его называют двучленом. Многочлен, состоящий из 3 одночленов, называют трехчленом.

Иногда в литературе используются такие термины, как «моном» (синоним «одночлена»), «бином» (синоним «двучлена»), «полином» (синоним «многочлена»).

Если известно значение переменных, входящих в полином, то возможно вычисление значения многочлена.

Пример. Найдем значение полинома x 3 +2x 2 +5y+1 при значении x=2 и y = 3.

Пример. Вычислим значение полинома v 4 – d 4 при значении переменных v = 4 и d = 3.

Стандартный вид многочлена

Иногда некоторые мономы, входящие в состав полинома, имеют одинаковую буквенную часть. Например, в выражении

первый и третий мономы отличаются лишь своими коэффициентами. Такие слагаемые называются подобными.

У подобных слагаемых одинаковый набор переменных, и при этом они возведены в одинаковые степени. Так, подобными являются мономы:

• 7a 2 s 3 и 2a 2 s 3 , так как совпадает буквенная часть a 2 s 3 ;
• 5v 9 m 7 t 5 и – 4v 9 m 7 t 5 , так как у них одинаковая буквенная часть – 4v 9 m 7 t 5 ;
• a 2 и 1000a 2 , так как есть одинаковая буквенная часть a 2 .

Также подобными слагаемыми можно считать и числа без буквенной части, например 8 и 2.

В качестве примеров неподобных слагаемых можно привести:

• 7a 2 s 3 и 2a 2 s 4 – у переменной s разные степени (3 и 4) в этих мономах;
• 4x 2 yи 5x 2 – в буквенной части первого монома есть переменная y, а у второго его нет.

У подобных слагаемых может быть изменен порядок множителей. Так, подобными являются мономы 5p 2 u 4 и 9u 4 p 2 , так как у одних и тех же переменных стоят одинаковые показатели.

Подобные слагаемые можно складывать друг с другом. В этом случае буквенная часть останется неизменной, а коэффициенты сложатся друг с другом. Например:

Такое действие называется приведением подобных слагаемых.

Пример. Приведите подобные слагаемые полинома:

Решение. В данном полиноме есть три пары подобных слагаемых:

Сгруппируем подобные слагаемые друг с другом, после чего сложим их:

Если в полиноме нет подобных слагаемых, а все входящие в него мономы записаны в стандартном виде, то его называют многочленом стандартного вида.

Что такое одночлен стандартного вида, можно узнать из ранее изученного урока. Примерами полиномов стандартного вида являются:

Далее рассмотрим понятие степени многочлена. Каждый из входящих в полином мономов имеет свой показатель степени(см. урок 3). Степенью полинома стандартного вида называется наибольшая из всех степеней одночленов, входящих в его состав.

Рассмотрим пример. Дан трехчлен 2y 2 + x 3 y + 5y 2 x, требуется найти его степень.

Решение. Рассматриваемый трехчлен находится в стандартном виде. Он состоит из трех мономов:

Найдем степень каждого из них:

• 2y 2 – степень равна 2;
• x 3 y – степень равна 4 = (3+1);
• 5y 2 x – степень равна 3 = (2+1).

Получается, что максимальную степень, равную 4, имеет моном x 3 y. Соответственно, и степень трехчлена также равна 4.

Если же рассматривается полином, не находящийся в стандартном виде, то для вычисления его степени сначала надо привести полином к этому виду.

Пример. Найдите степень полинома с 6 + ac 2 + 9 – с 6 .

Решение. На первый взгляд может показаться, что она равна 6, так как один из его мономов, с 6 , имеет показатель, равный 6. Но это не так. Приведем полином к стандартному виду:

Оказалось, что подобные мономы c 6 и – с 6 сократились. Получившийся полином состоит из двух мономов, ac 2 и 9, чьи степени равны 3 и 0 соответственно. Значит, и степень всего двучлена равна трём.

Определение степени полинома потребуется для решения уравнений в старших классах. Если в одной части уравнения стоит полином, например, третьей степени, в другой части – ноль, то его называют уравнением третьей степени:

Аналогично выделяют уравнения первой, второй, четвертой и любой другой степени.

В зависимости от степени уравнения используются различные методы их решения. Ранее (ссылка на урок уравнения) мы уже научились решать линейные уравнения, которые являются уравнениями 1-ой степени. Обычно чем выше степень уравнения, тем сложнее его решать. Также существует интересная зависимость – количество корней уравнения не превышает его степень (за исключением одного частного случая, при котором есть бесконечное множество решений).

Особое значение в алгебре имеют те полиномы, в которых содержится только одна переменная, например:

• m 2 + 4m 4 + 5m 3 +9(здесь переменная m);
• c 6 + 1(единственная переменная – с);
• 3x + 10(запись содержит только x);
• – y 4 + 89y 10 – 2,56y 100 (используется только y).

Их называют полиномами с одной переменной. Обычно их принято записывать по мере убывания степеней одночленов. То есть впереди пишется моном с максимальной степенью, а в самом конце – число без буквенной части:

То число, которое стоит перед одночленом в наибольшей степени, называют старшим коэффициентом, а число, не имеющее буквенной части – свободным членом (реже свободным коэффициентом):

Для некоторых полиномов с одной переменной есть особое название. Так, многочлен второй степени называют квадратным трехчленом. Дело в том, вторую степень в математике часто называют квадратом, а состоит квадратный трехчлен из трех монов. В качестве примера можно привести:

Конечно, квадратный многочлен может содержать и меньше трех одночленов:

В этом случае иногда бывает удобно добавить «недостающее» слагаемое, поставив перед ним коэффициент, равный нулю:

В общем случае квадратным трехчленом называют выражение вида

где x – произвольная переменная, а, b и c являются произвольными действительными числами. При этом a не должно равняться нулю, иначе получится полином уже только 1-ой степени.

Квадратные трехчлены будут изучены подробнее в старших классах при изучении темы «Квадратные уравнения».

Сложение и вычитание многочленов

Полиномы можно складывать друг с другом, а также вычитать. При этом, возможно, придется приводить подобные слагаемые.

Пример. Произведите сложение многочленов 8z 2 + 3z +12 и 2z 4 + 9z.

Решение. Запишем интересующую нас сумму:

Если перед скобками стоит знак «+», то можно просто опустить скобки:

Осталось привести полином к стандартному виду. Здесь есть лишь одна пара подобных одночленов, 3z и 9z:

При вычитании многочленов надо учитывать следующее правило:

Пример. Вычтите из полинома x 5 + 3x 3 – 7y 3 + 9x 2 + 17 трехчлен 2y 4 + 0,4y 3 – 25.

Запишем разность полиномов:

Первые скобки можно опустить, так как перед ними нет никакого знака. Перед вторыми скобками стоит минус, а потому для раскрытия скобок знаки слагаемых в них надо поменять на противоположные. Вместо 2y 4 надо написать – 2y 4 , вместо 0,4y 3 поставим – 0,4y 3 , а – 25 заменим на + 25:

Осталось привести подобные слагаемые:

Стоит заметить, что при сложении и вычитании полиномов их степени не могут увеличиться. Так, если складываются два полинома 5-ой и 4-ой степени, то в результате получится многочлен, чья степень будет не больше 5.

Рассмотрим более сложный пример с вложенными (внутренними) скобками. Необходимо упростить выражение

Решение. Раскроем первые скобки. Перед ними стоит минус, поэтому знаки слагаемых должны поменяться на противоположные. Однако обратите внимание, что здесь есть вложенные скобки (2a 2 b – ab) и (ab 2 + 2a 2 b). Менять следует только знак перед ними, а знаки внутри вложенных скобок не меняются! Они рассматриваются как единые, неизменяемые слагаемые:

Теперь раскроем оставшиеся две скобки:

Приведем подобные слагаемые. Для наглядности пары подобных мономов подчеркнуты. Одной чертой подчеркнуты мономы с буквенной частью ab 2 , двумя чертами – мономы с a 2 b, а штриховой линией выделены мономы с буквенной частью ab:

Умножение одночлена на многочлен

Напомним распределительный закон умножения:

Используя этот закон, можно производить умножение одночлена на многочлен.

Пример. Перемножьте выражения 5v 2 и 9v 3 + 2t 4 .

Решение: Запишем произведение выражений:

Такое раскрытие скобок можно объяснить с помощью «метода фонтанчика»:

От множителя 5v 2 строят линии (синего цвета к) КАЖДОМУ слагаемому в скобке. Каждой такой линии соответствует отдельное произведение в получаемом полиноме.

После раскрытия скобок получили два произведения одночлена на одночлен, которые считаем по отдельности (см. урок 3):

Можно сформулировать следующее правило умножения многочлена на одночлен:

Ещё один пример. Перемножьте полином 2x 2 y + 4xy 2 – 1 и моном – 3ху.

Здесь метод «фонтанчика» будет выглядеть так:

Можно заметить, что после умножения монома на полином получится столько одночленов, сколько их было в исходном полиноме. Это правило можно использовать для самоконтроля.

Умножение многочлена на многочлен

Пусть нам надо перемножить два полинома, a+bи c+d. Запишем их произведение:

Заменим выражение a + b переменной k:

Теперь исходное произведение можно выразить как произведение монома и полинома:

Проведем обратное преобразование, заменив k на a + b:

Наконец, раскроем скобки в этом выражении:

Эту формулу можно проиллюстрировать геометрически. Рассмотрим прямоугольник со сторонами a + b и c + d:

Площадь этого прямоугольника, как и любого другого, равна произведению его сторон, то есть(a + b)(c + d).С другой стороны, она состоит из 4 прямоугольников, чьи площади также вычисляются как произведения их сторон, и составляют ac, bc, ad и bd. Поэтому можно записать равенство

Получается, что для умножения многочлена на многочлен нужно перемножать попарно все мономы, входящие в их состав, после чего сложить их.

Если в одном полиноме содержится m слагаемых, а в другом n, то результатом их перемножения окажется новый полином, содержащий m•n мономов (до приведения подобных слагаемых). Для перемножения многочленов также используется метод «фонтанчика».

Пример. Найдем произведение выражений 3a 2 – 4ab + b 2 и 2a– b.

Решение: В первом полиноме содержится 3 монома, а во втором – 2, поэтому после их перемножения мы получим сумму 3•2 = 6 одночленов:

Раскрытие скобок «фонтанчиком» будет выглядеть так:

В результате действительно получилась сумма 6 мономов. Осталось вычислить каждый из них, после чего привести подобные слагаемые:

Заметим, что при перемножении полиномов происходит сложение степеней многочленов. Действительно, в рассмотренном выше примере мы умножили полином второй степени 3a 2 – 4ab + b 2 на полином первой степени 2a– b, и получили в результате многочлен 3-ей (2+1) степени.

Также возможно умножение многочленов в столбик. Особенно это удобно делать в случае с полиномами с одной переменной.

Пример. Найдите произведение выражений 2x 3 + 3x 2 +5x + 9 и x 2 + 4x + 7.

Решение: Запишем полиномы в столбик, один под другим:

Далее умножим самый правый моном второго многочлена, то есть число 7, на первый полином, и запишем его ниже:

Далее умножим следующий моном, 4х, на первый полином, и запишем результат ещё ниже, причем сместим запись чуть влево, чтобы подобные члены оказались друг под другом:

Также умножим последний одночлен, x 2 , на первый полином:

Осталось сложить подобные слагаемые (то есть переменные х с одинаковыми степенями), которые записаны друг под другом:

Ещё раз цветом выделим подобные слагаемые и результаты их суммирования:

Ответ: 2х 5 + 11х 4 + 31х 3 + 50х 2 + 71х +63.

Источник