Способ раскатки применяется для построения разверток

При построении разверток данным способом поверхность цилиндра или призмы разрезается по одной из образующих или по одному ребру и совмещается вращением вокруг образующей или вокруг ребра с некоторой плоскостью.

Данный способ обычно применяется в случае, когда образующие цилиндра или ребра призмы являются линиями уровня. Если образующие цилиндра или ребра призмы не являются линиями уровня, то предварительно одним из способов преобразования комплексного чертежа их надо привести в положение линий уровня.

Рассмотрим построение чертежа развертки поверхности призмы, ребра которой являются фронтальными линиями уровня, а нижнее основание является горизонтальной плоскостью уровня (рис. 153).

Призма разрезана по ребру a(a₁,a₂) и это ребро принято за ось вращения i(i₁,i₂); i=α. При вращении граней призмы вокруг этой оси любая точка будет перемещаться в плоскости, перпендикулярной оси вращения, например, точка B будет перемещаться в плоскости

Грань ABB’A поворачивают до совмещения ее с плоскостью уровня α(α₁), проходящей через ребро a. Для этого достаточно совместить точку B с плоскостью α. Зная расстояние от точки A до точки B (/AB/=/A₁B₁/ ) и зная, что точка B перемещается во фронтально-проецирующей плоскости δ(δ₂), из точки A₂, как из центра, проводится дуга окружности радиусом r=/A₁B₁/ и на δ₂ получается точка B₀. Точка B₀ – совмещенное с плоскостью α положение точки B. Соединив точки A₂ и B₀, получим совмещенное положение грани с плоскостью α.

Для того чтобы совместить грань ABB’A’ с плоскостью α, из точки B₀ строится прямая b₀ (b₀ – совмещенное положение ребра b с плоскостью α) параллельно a₂. Аналогичным образом построены совмещенные положения остальных граней призмы с плоскостью  (равенство соответствующих отрезков обозначено на рис 153 специальными значками).

Вершины A’, B’ и C’ верхнего основания также вращаются в соответствующих фронтально-проецирующих плоскостях, перпендикулярных ребрам призмы. Поэтому совмещенные с плоскостью α проекции вершин верхнего основания A’₀, B’₀ и C’ определяются как точки пересечения прямых a₀, b₀ и c₀ с соответствующими фронтально-проецирующими плоскостями.

Соединив последовательно совмещенные вершины ломаными линиями, получают развертку боковой поверхности призмы.

Чтобы получить полную развертку поверхности призмы, к развертке боковой поверхности присоединяют натуральные величины обоих оснований.

На рис 146 показано построение на чертеже развертки точки K(K₁,K₂), принадлежащей грани ABB’A’.

Для этого через точку K проведена прямая (KD) , параллельная ребрам призмы. Затем она построена на чертеже развертки: где K₀ – точка развертки, соответствующая точке K поверхности.

Рассмотрим построение чертежа развертки поверхности наклонного цилиндра, образующие которого являются фронтальными линиями уровня, а основание – окружностью (рис. 154).

Для построения развертки цилиндр разрезается по образующей AA’, а основание цилиндра разбивается на произвольное число равных частей, что соответствует замене цилиндрической поверхности поверхностью многогранной призмы. Следует иметь в виду, что чем больше число сегментов, тем точнее развертка поверхности.

В данном примере основание разбито на шесть равных частей точками A, B, C, D, E и F. Эти точки совмещены с плоскостью γ(γ₁) вращением вокруг оси i(i₁,i₂), которая совпадает с образующей цилиндра AA’.

При вращении граней вписанной призмы вокруг оси i, любая точка будет перемещаться в плоскости, перпендикулярной оси вращения, например, точка B будет вращаться в плоскости δ(δ₂) ⊥ i(δ₂ ⊥ i₂). Зная расстояние от точки A до точки B (AB=A₁B₁) и зная, что точка B перемещается во фронтально – проецирующей плоскости δ(δ₂), можно провести дугу окружности из точки A₂, как из центра, радиусом r = A₁B₁ и получить на δ₂ точку B₀. Точка B₀ – совмещенное с плоскостью γ положение точки B.

Аналогичным образом построены совмещенные положения остальных точек основания цилиндра. Образующие цилиндра на развертке параллельны своим фронтальным проекциям.

Оставшуюся неподвижной точку A и полученные точки, B₀, C₀, D₀, E₀, F₀ и A₀ нужно соединить плавной кривой. Эта кривая представляет собой развертку окружности, лежащей в основании цилиндра.

Источник

Способ раскатки

Разверткой многогранника называется плоская фигура, получаемая последовательным совмещением всех граней многогранника с одной плоскостью. Так как все грани многогранника изображаются на развертке в натуральную величину, построение развертки сводится к определению натуральной величины граней – плоских многоугольников.

Способ раскатки используют для построения развертки призмы, в том случае, когда ее основание параллельно какой-либо одной плоскости проекции, а боковые ребра отображаются в натуральную величину на другой плоскости проекций.

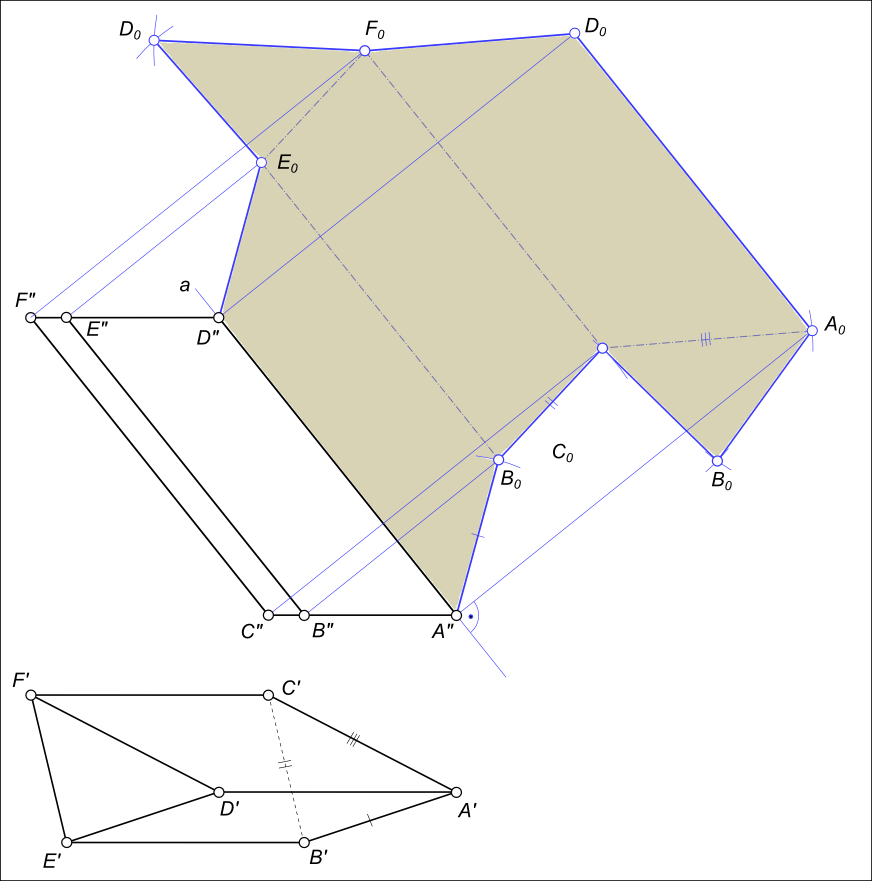
Построить развертку поверхности наклонной трехгранной призмы ABCDEF, используя способ раскатки

За плоскость развертки примем плоскость β, проходящую через ребро AD, параллельную фронтальной плоскости проекций. Совместим грань ADEB с плоскостью β. Для этого мысленно разрежем призму по ребру AD, и затем выполним поворот грани ADEB вокруг ребра AD. Определение совмещенного с плоскостью β положения ребра B₀E₀ из точки B» опускаем луч, перпендикулярный к A»D» и засекаем на нем дугой радиуса A`B`, проведенной из центра A», точку B₀. Из точки B₀ проводим прямую B₀E₀, параллельную A»D». Совмещенное положение ребра B₀E₀ принимаем за новую ось и вращаем вокруг нее грань BEFC до совмещения с плоскостью β. Из точки C» опускаем луч, перпендикулярный к B»E», а из точки B₀ — дугой окружности радиусом B`C` засекаем на нем положение точки C₀. Из C₀ проводим C₀F₀ параллельно B₀E₀. Аналогично определяется положение ребра A₀D₀. Соединив точки A»B₀C₀A₀ и D»E₀F₀D₀ прямыми, получим фигуру A»B₀C₀A₀D₀E₀F₀D» — развертку боковой поверхности призмы. Полная развертка призмы будет получена если к каким-либо из звеньев ломаных линий A»B₀C₀A₀ и D»E₀F₀D₀ пристроить треугольники основания A₀B₀C₀ и D₀E₀F₀.

Способ раскатки применяется также для получения развертки цилиндрической поверхности: Развертка цилиндра

Источник

Способ раскатки

Способ раскатки применяется для построения разверток призматических и цилиндрических поверхностей в случае, когда боковые ребра призмы или образующие цилиндра параллельны какой-либо плоскости проекций, следовательно, проецируются в натуральную величину, а стороны основания параллельны другой плоскости проекций.

Схема построения развертки:

1. Мысленно разрезается боковая поверхность по одному из ребер.

2. Последовательным вращением вокруг боковых ребер, как вокруг линий уровня, все боковые грани совмещаются с плоскостью уровня, проходящей через ребро, по которому разрезается данная призма.

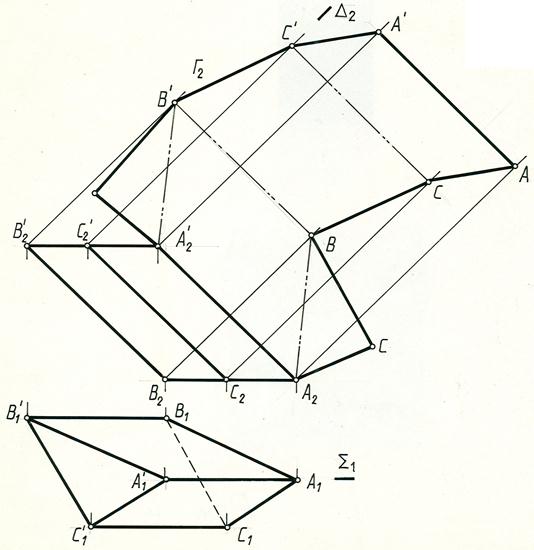
Пример 5. Построить полную развертку поверхности наклонной треугольной призмы.

Решение: Развертку боковой поверхности призмы строим способом раскатки, так как боковые ребра ее параллельны фронтальной плоскости проекций, а стороны основания параллельны горизонтальной плоскости проекций и проецируются в натуральную величину (рис. 12.6)

Так как боковые ребра параллельны фронтальной плоскости П₂, можно каждую грань повернуть вокруг соответствующего ребра до положения, когда эта грань окажется параллельна плоскости П₂. Тогда она и спроецируется на плоскость П₂ без искажения. Повернув таким образом каждую грань, получим развертку боковой поверхности призмы.

Примем за плоскость развертки плоскость Σ (Σ₁), проходящую через ребро АА’, и параллельную фронтальной плоскости проекций. Совместим грань АА’В’В с плоскостью Σ. Для этого мысленно разрежем поверхность призмы по ребру АА’ и повернем грань АА’В’В вокруг ребра (как вокруг фронтали) до совмещения с фронтальной плоскостью Σ, проходящей через это ребро.

Для определения совмещенного положения ребра ВВ’ с плоскостью Σ, из точки В₂‘ проводим вырожденную проекцию плоскости Г(Г₂) , в которой вращается точка В’, (см. метод вращения вокруг линии уровня) перпендикулярную АА’, на которой из точки А’₂ делаем засечку дугой окружности радиуса A₂‘B’=A₁B₁. Через точку В’ проводим прямую В’В параллельную А’А. Принимаем совмещенное положение ребра В’В за новую ось и вращаем вокруг нее грань В’ВСС’ до совмещения с плоскостью Σ. Для этого из точки C₂‘ проводим вырожденную проекцию плоскости Δ (Δ₂) перпендикулярную ребру ВВ’, а из точки В’ – дугу окружности радиусом равным B₁C₁. Пересечение дуги с Δ ₂ определит положение точки С’. Аналогично определяем положение ребра А’А. Соединив соответствующие точки прямыми линиями, получим развертку боковой поверхности призмы. Достроив основание призмы, получим полную развертку.

Источник

Развёртывание поверхностей

Содержание:

Развертывание цилиндров и конусов основывается на способах развертки гранных поверхностей приведенных выше. В общем случае поверхность цилиндра аппроксимируется призматической поверхностью, а конус – пирамидой и затем строится приближенная развертка кривой поверхности.

Свойства развёрток

Развёрткой криволинейной поверхности Ф называется плоская фигура , полученная путём совмещения поверхности Ф с плоскостью Σ (рис. 5.1). В начертательной геометрии плоскостью Σ является одна из плоскостей проекций.

Развёртывание поверхностей тел широко применяется в технике, поскольку большое количество технических конструкций изготавливается из листового материала. Заготовки таких конструкций, которые являются развёртками, используются для изготовления тонкостенных ёмкостей, воздуходувов, промышленной вентиляции и пневмотранспорта, фасонных частей пылеулавливателей, деталей подъёмно — транспортных приборов и т.д. (рис. 5.2).

Развёртывание поверхности

Применение развёрток

Поверхности Ф, которые можно совместить с плоскостью Σ без разрывов и складок, являются, развёртывающимися. К ним принадлежат все многогранники (см. п. 4.1), цилиндрические и конические поверхности (см. п. 3.2.1.3, рис. 3.55 б – в), торсы (см. п. 3.2.1.3, рис. 3.57). Все другие кривые поверхности не развёртываются на плоскость, поэтому при их изготовлении из листового материала они приближённо заменяются развёртывающимися поверхностями (призмами, пирамидами, цилиндрами, конусами). В этих случаях имеют место так называемые условные развёртки (см. п. 5.4.1.3 – 5.4.1.4).

Основные свойства развёрток:

а) прямая l на поверхности Ф отвечает прямой на развёртке

б) параллельные прямые на поверхности Ф отвечают параллельным прямым на развёртке

в) длина (натуральная величина) любой линии s на поверхности Ф равна длине линии на развёртке

г) угол α между линиями r, s на поверхности Ф равен углу между линиями на развёртке

д) площадь S фигуры на поверхности Ф равна плоскости соответствующей фигуры на развёртке

е) если прямая на развёртке отвечает кривой линии s на поверхности Ф, то кривая s является геодезическою линией поверхности Ф. Длина дуги МN геодезической линии является наименьшей из всех возможных дуг MN на поверхности Ф.

Описанные свойства геометрически интерпретированы на рис. 5.3.

Свойства развёрток

Геодезическая линия (от греческого γεωδαισία – разделение Земли) – линия минимальной длины, проведенная через две точки криволинейной поверхности. На развёртке поверхности эта линия — прямая.

Геодезическая линия широко применяется в неэвклидовой геометрии, теоретических и практических задачах геодезии – науки, которая изучает измерения пространства, в том числе размеры и форму Земли, её гравитационное поле и т.д.

Развёртывание поверхности многогранника

Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью. Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.

Способ натуральных граней

Согласно свойствам развёртки (см. п. 5.1) все грани многогранника Ф сохраняют на развёртке свою длину, для определения которой используются способы начертательной геометрии.

На рис. 5.4 построены горизонтальная и фронтальная проекции треугольной пирамиды SABC. Основа АВС является плоскостью горизонтального уровня, поэтому проецируется на П1 в натуральную величину А1В1С1. Для определения натуральных величин граней SAB, SBC, SCA используется способ вращения вокруг горизонтально-проецирующей оси і, которая проходит через вершину S пирамиды. Отрезки являются натуральными величинами ребер SA, SB, SC пирамиды. По этим ребрам строится развёртка пирамиды. Вырезав плоскую заготовку из контура развёртки и сложив её по линиям сгиба и совмещая одноименные рёбра, можно получить поверхность данной пирамиды SABC.

Способ натуральных граней

Для определения на развёртке произвольной точки D пирамиды применяется способ вспомогательного отрезка. Точка D принадлежит грани SАС. Через вершину S и точку D проводится отрезок S-1, точка 1 которого принадлежит основе АВС пирамиды. Определяется натуральная величина отрезка S-1, на нём определяется проекция На отрезке развёртки строится отрезок , длина которого равна длине проекции

Способ нормального сечения

Способ нормального сечения применяется для построения развёртки призм, ребра которых являются прямыми уровня.

Суть способа нормального сечения

Призма пересекается в произвольном месте плоскостью Σ, перпендикулярной рёбрам. Определяется натуральная величина линии 1 – 2 – … нормального сечения. Эта линия является плоским многоугольником, количество сторон которого равно количеству граней призмы. Линия 1 – 2 – … разворачивается до формы прямого отрезка … На перпендикулярах, проведенных по обе стороны от точек …, строятся части натуральных величин рёбер пирамиды, которые находятся по разные стороны секущей плоскости Σ.

На рис. 5.5 заданы две проекции треугольной призмы ABCDEF с рёбрами AD, BE, CF горизонтального уровня. Вводится секущая плоскость Σ, перпендикулярная рёбрам призмы (горизонтальный след Σ1 перпендикулярен горизонтальным проекциям рёбер призмы). Плоскость Σ пересекает призму по треугольнику 1 – 2 – 3, точки которого принадлежат, соответственно, рёбрам AD, BE, CF. Способом замены плоскостей проекций определяется натуральная величина нормального сечения (ось параллельна следу Σ1). Треугольник разворачивается до формы прямого отрезка длины частей которого равны соответствующим сторонам треугольника На перпендикулярах, проведенных по обе стороны от точек строятся отрезки длины которых равны длинам проекций На развёртке достраиваются натуральные величины основ АВС, DEF призмы.

Способ нормального сечения

Для определения на развёртке произвольной точки G призмы применяется способ вспомогательных отрезков. Точка G принадлежит грани ABDE. Через точку G проводится отрезок 4 – 5, параллельный рёбрам призмы. Точка 4 принадлежит отрезку АВ, точка 5 – отрезку DE. Определяется точка 6 пересечения отрезка 4 – 5 с плоскостью Σ. Точка 6 принадлежит отрезку 1 – 2. Определяется проекция На отрезке развёртки строится отрезок , длина которого равна длине проекции Из точки развёртки призмы проводится отрезок в направлении, перпендикулярном отрезку в сторону точки Длина отрезка равна длине проекции

Способ раскатки

Способ раскатки применяется для развёртывания призмы, основа которой параллельна одной плоскости проекций, а боковые рёбра параллельны другой плоскости проекций.

Из точек 1, 2, … основы … верхней грани призмы проводятся лучи, перпендикулярные боковым рёбрам … На этих лучах строятся точки … так, что длины отрезков … равны натуральным величинам отрезков , …

На рис. 5.6 заданы две проекции треугольной призмы с основой 1 – 2 – 3 и верхней гранью горизонтального уровня и рёбрами фронтального уровня. Из фронтальных проекций проводятся лучи, перпендикулярные фронтальным проекциям На этих лучах по очереди откладываются точки так, что длины отрезков равны натуральным величинам отрезков

Способ раскатки

Для определения на развёртке произвольной точки А призмы применяется способ вспомогательного луча. Точка А принадлежит грани Через точку А проводится отрезок параллельный рёбрам призмы, точка 4 которого принадлежит отрезку 1 – 3 основы. Из проекций проводятся лучи перпендикулярные фронтальным проекциям рёбер призмы. Из точки принадлежащей отрезку развёртки, проводится отрезок параллельный отрезку до пересечения с лучом

Развёртывание поверхностей тел вращения

По развертыванию поверхности делятся на два класса: развертываемые, которые можно совместить с плоскостью без разрывов и складок, и неразвертываемые, которые невозможно совместить с плоскостью без разрывов и складок. Развертываются все многогранные поверхности, из кривых поверхностей – только линейчатые, у которых смежные образующие параллельны между собой (цилиндрические) или пересекаются по одной точке (конические).

Из всего разнообразия поверхностей тел вращения точное развёртывание осуществляется только для прямых круговых цилиндра и конуса (рис. 5.7 – 5.8).

Поверхность прямого кругового цилиндра разворачивается в прямоугольник, одна сторона которого равна длине нормального сечения (окружности диаметром d), другая – высоте h цилиндра (рис. 5.7). Развёртка цилиндра при необходимости дополняется нижней и верхней основами – окружностями диаметром d. Для определения точки А на развёртке прямого кругового цилиндра применяется способ образующей линии. Определяется угол α, и строится образующая линия на развёртке. Она размещена на расстоянии Высота точки равна высоте точки А.

Развёртка цилиндра

Поверхность прямого кругового конуса разворачивается в сектор окружности с центром в вершине S конуса. Радиус сектора равен длине l образующей линии конуса; угол φ = 180°·d/l, где d – диаметр основы конуса (рис. 5.8). Развёртка конуса при необходимости дополняется основой – окружностью диаметром d. Для определения точки А на развёртке прямого кругового конуса применяется способ образующей линии. Определяется угол α и строится образующая линия на развёртке, положение которой определяется углом β = 0,5αd/l. Точка расположена на расстоянии равном натуральной величине отрезка SA.

Развёртка конуса

Приближённое и условное развёртывание кривых поверхностей

При построении приближенных и условных разверток используют ап-проксимацию (от approximare (лат.) – приближаться) одной поверхности к другой. Аппроксимацией называют замену одной поверхности другой – аппроксимирующей, которая приближается к заданной по каким-то опре-деленным свойствам (форма, площадь, кривизна) с той или иной степенью точности.

Способ аппроксимирующих поверхностей

Развёртка любой развёртывающейся поверхности (кроме прямых круговых конуса и цилиндра) строится приближённо. Это происходит вследствие того, что при развёртывании кривой поверхности её аппроксимируют гранями вписанных многогранников(рис. 5.9).

Способ призматических поверхностей

Например, цилиндрическая поверхность условно заменяется призмой (рис. 5.9 а), коническая поверхность – пирамидой (рис. 5.9 б).

– Аппроксимация тела вращения многогранником

Для построения приближённой развёртки цилиндрической поверхности используется способ призматических поверхностей

Суть способа призматических поверхностей

В цилиндрическую поверхность вписывается призма, количество граней которой прямо влияет на точность построения развёртки цилиндра. Строится развёртка этой призмы способом нормального сечения или раскатки (см. п. 5.2.2 – 5.2.3). Через точки на развёртке призмы проводятся плавные кривые, являющиеся контуром приближённой развёртки цилиндра. При необходимости развёртка цилиндра дополняется нижней и верхней основами.

На рис. 5.10 изображен комплексный чертёж эллиптического цилиндра, поверхность которого аппроксимируется двенадцатигранной призмой. Развёртка последней строится способом раскатки. Через точки проводятся плавные кривые (синусоиды), образующие контур развёртки цилиндра. Развёртка дополняется нижней и верхней основами цилиндра.

Способ пирамидальных поверхностей

Способ пирамидальных поверхностей используется для построения развёртки боковой поверхности конуса.

Суть способа пирамидальных поверхностей

В коническую поверхность вписывается пирамида. Строится приближённая развёртка этой пирамиды способом натуральных граней (см. п. 5.2.1). Через точки на развёртке пирамиды проводится плавная кривая, являющаяся контуром развёртки конуса. По необходимости развёртка конуса дополняется его основой.

Аппроксимация (от англ. approximation – приближение) – научный метод, состоящий в замене одних объектов другими, более простыми, приближёнными к оригиналу.

Необходимо различать такие понятия, как приближённая и условная развёртка. Приближённая развёртка касается развёртывающихся поверхностей. Условная развёртка строится для поверхностей, которые не развёртываются.

Развёртка эллиптического цилиндра

На рис. 5.11 изображен комплексный чертёж эллиптического конуса, поверхность которого аппроксимируется двенадцатигранной пирамидой. Развёртка последней строится способом натуральных граней. Через точки проводится плавная кривая, которая образует контур развёртки конуса. Развёртка дополняется основой конуса.

Развёртка эллиптического конуса

Способ цилиндрических поверхностей

Для поверхностей, которые не развёртываются. в том числе нелинейчатых, строятся условные развёртки. Основные способы построения условных развёрток такие:

а) способ цилиндрических поверхностей;

б) способ конических поверхностей;

в) метод триангуляции.

Суть способа цилиндрических поверхностей

Кривая поверхность описывается совокупностью цилиндрических поверхностей, которые в дальнейшем развёртываются и совмещаются по точкам и линиям. Полученная развёртка является условной развёрткой кривой поверхности.

На рис. 5.12 построена условная развёртка сферы. Вокруг её поверхности описываются шесть одинаковых цилиндрических поверхностей. Одна из таких поверхностей имеет образующие линии Длины этих образующих равны длинам их горизонтальных проекций .Расстояния между образующими одинаковы и равны длине дуги SA, то есть длине фронтальной проекции Развёрткой одной из шести цилиндрических поверхностей является фигура в форме лепестка, контур которой проходит через концы образующих линий, удалённых одна от другой на одинаковое расстояние, равное длине дуги . Прибавляя к полученной части еще пять, строится условная развёртка сферы.

Условная развёртка сферы.

На рис. 5.13 построена условная развёртка открытого тора. Вокруг его поверхности описываются двенадцать одинаковых цилиндрических поверхностей. Одна из таких поверхностей имеет образующие линии Длины этих образующих равны длинам их фронтальных проекций Расстояния между образующими одинаковы и равны длине дуги SA, то есть, длине горизонтальной проекции S1A1. Развёрткой одной из двенадцати цилиндрических поверхностей является фигура, контур которой проходит через концы образующих линий, удалённых одна от другой на одинаковое расстояние, равное длине дуги S1A1. Прибавляя к полученной части еще одиннадцать, строится условная развёртка тора.

Условная развёртка открытого тора

Способ конических поверхностей

Способ конических поверхностей используется для построения условных развёрток закрытых тел вращения (эллипс, параболоид, эллипсоид, двуполостной гиперболоид, закрытый тор и т.д.).

Суть способа конических поверхностей

Сегменты поверхности описываются совокупностью конических поверхностей, которые развёртываются и совмещаются по точкам и линиям. Полученная развёртка является условной развёрткой кривой поверхности.

На рис. 5.14 построена условная развёртка сферы. Вокруг её поверхности описывается одна цилиндрическая и шесть конических поверхностей с разными вершинами Длины образующих линий одинаковы и равны длине проекции Углы и радиусы развёртывания конусов определяются, как описано в п. 5.3.

Условная развёртка сферы

На рис. 5.15 построена условная развёртка эллипсоида. Вокруг его поверхности описываются одна цилиндрическая и шесть конических поверхностей с разными вершинами Длины образующих линий могут быть разными и определяются по их фронтальным проекциям. Углы и радиусы развёртывания конусов определяются, как показано в п. 5.3.

Условная развёртка эллипсоида

Метод триангуляции

Метод триангуляции (от англ. triangle – треугольник) применяется для развёртывания многогранников, приближенного развёртывания цилиндрических и конических поверхностей и поверхностей с ребром поворота (торсов), а также условного развёртывания поверхностей которые не развёртываются.

Суть метода триангуляции

Кривая поверхность разбивается на треугольники с общими сторонами. Натуральные величины этих треугольников сочетаются по общим сторонам. Внешний контур полученной плоской фигуры является приближенной или условной развёрткой заданной кривой поверхности.

На рис. 5.16 построена приближённая развёртка торса Ф. Последний разбивается совокупностью треугольников с вершинами 1, 2, …, принадлежащими ребру возврата и одной из линий l поверхности Ф. Натуральные величины сторон 1 – 2, 2 – 3, … треугольников определяются способом вращения вокруг проецирующей оси. По найденным отрезкам строятся натуральные величины треугольников 1 – 2 – 3, 2 – 3 – 4, …, которые сочетаются по общим сторонам. Контур полученной плоской фигуры является приближенной развёрткой торса Ф.

Приближённая развёртка торса

На рис. 5.17 построена приближённая развёртка поверхности произвольного пространственного тела. Его поверхность разбивается на треугольники, стороны которых построены по точкам 1, 2, …, А, В, …, принадлежащим соответственно верхней и нижней основам тела. Натуральные величины сторон треугольников определяются способом вращения вокруг горизонтально-проецирующих осей, проходящих через точки В, С. По найденным отрезкам строятся натуральные величины треугольников, которые сочетаются по общим сторонам. Контур полученной плоской фигуры является приближенной развёрткой поверхности тела.

Развёртка поверхности тела методом триангуляции

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник