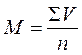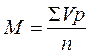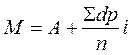Виды средних величин, методика их вычисления



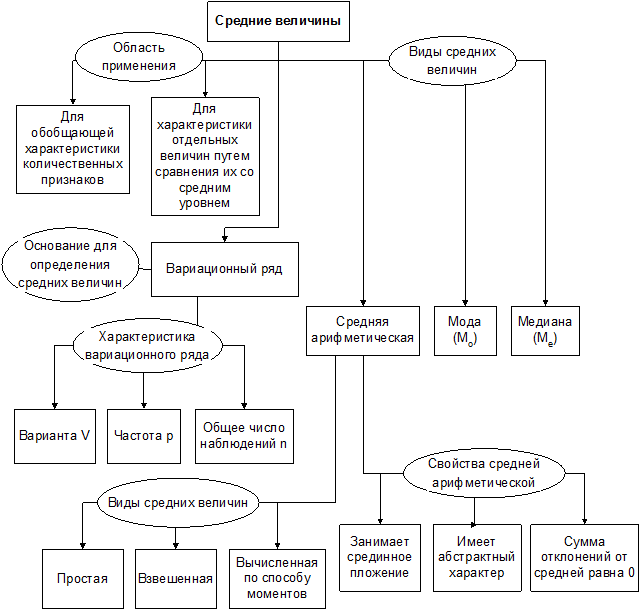
Различают три вида средних величин: мода (Мо), медиана (Me), средняя арифметическая (М). Они не могут подменить друг друга и лишь в совокупности достаточно полно и в сжатой форме представляют собой особенности вариационного ряда.
Мода (Мо) — наиболее часто встречающаяся в ряду распределения варианта. Она дает представление о центре распределения вариационного ряда. Используется:
— для определения центра распределения в открытых вариационных рядах
— для определения среднего уровня в рядах с резко асимметричным распределением
Медиана — это серединная варианта, центральный член ранжированного ряда. Название медиана взято из геометрии, где так именуется линия, делящая сторону треугольника на две равные части.
— для определения среднего уровня признака в числовых рядах с неравными интервалами в группах
— для определения среднего уровня признака, когда исход-ные данные представлены в виде качественных признаков и когда единственным способом указать некий центр тяжести совокупности является указание варианты (группы вариант), которая занимает центральное положение
— при вычислении некоторых демографических показателей (средней продолжительности предстоящей жизни)
— при определении наиболее рационального места расположения учреждений здравоохранения, коммунальных учреждений и т. п. (имеется в виду учет оптимальной удаленности учреждений от всех объектов обслуживания)
В настоящее время очень распространены различные опросы ((маркетинговые, социологические и др.), в которых опрашиваемых просят выставить баллы изделиям, политикам и т. п. Затем из полученных оценок рассчитывают средние баллы и рассматривают их как интегральные оценки, выставленные коллективом опрошенных. При этом обычно для определения средних показателей применяют среднее арифметическое. Однако такой способ на самом деле применять нельзя. Обоснованным в этом случае является использование в качестве средних баллов медианы или моды.
Для характеристики среднего уровня признака наиболее часто используется в медицине средняя арифметическая величина (М).
Средняя арифметическая величина— это общая количественная характеристика определенного признака изучаемых явлений, составляющих качественно однородную статистическую совокупность. Различают среднюю арифметическую простую и взвешенную.
Средняя арифметическая простая вычисляется для не сгруппированного вариационного ряда путем суммирования всех вариант и делением этой суммы на общее количество вариант, входящих в вариационный ряд.
Вычисляется средняя арифметическая простая по формуле:
М — средняя арифметическая простая,
ΣV — сумма вариант,
n — число наблюдений
Средняя арифметическая взвешенная вычисляется для сгруппированного вариационного ряда по формуле:
М — средняя арифметическая взвешенная,
ΣVp — сумма произведений вариант на их частоты,
n — число наблюдений.
Возвращаясь к нашему примеру, определим среднюю частоту пульса (среднее число ударов в минуту) у 54 студентов перед экзаменом.
| M = | 60х1+62х2+64х3+66х3+68х3+70х9+72х6+74х7+76х11+78х5+80х4 | = | =72,3(ударов в минуту) |
Помимо указанного метода прямого расчета средней арифметической взвешенной, существуют другие методы, в частности, способ моментов при котором несколько упрощены арифметические расчеты.
Расчет средней арифметической способом моментов проводится по формуле:
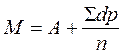
A – условная средняя (чаще всего в качестве условной средней берется мода Мо)
d – отклонение каждой варианты от условной средней (V–А)
Σdр — сумма произведений отклонений на их частоту.
Порядок вычисления представлен в таблице (за условную среднюю принимаем Мо = 76 ударам в минуту).
Определение средней арифметической способом моментов
| частота пульса V | Р | d (V–A) | dp |
| –16 | –16 | ||
| –14 | –28 | ||
| –12 | –36 | ||
| –10 | –30 | ||
| –8 | –24 | ||
| –6 | –54 | ||
| –4 | –24 | ||
| –2 | –14 | ||
| n = 54 | Σdp= –200 |
| M = 76 + | –200 | = 76–3,7 = 72,3 (ударов в минуту) |
Среднюю арифметическую можно также рассчитать и по данным середины группы. С учетом интервала между группами. Расчет проводим по формуле:

где i — интервал между группами.
Порядок вычисления представлен в табл. (за условную среднюю принимаем Мо = 73 ударам в минуту, где i = 3)
Определение средней арифметической способом моментов
| частота пульса V | середина группы | частота Р | условное отклонение в интервалах (d) | произведение условного отклонения на частоту (dp) |
| 60–62 | –4 | –12 | ||
| 63–65 | –3 | –9 | ||
| 66–68 | –2 | –12 | ||
| 69–71 | –1 | –9 | ||
| 72–74 | ||||
| 75–77 | ||||
| 78–80 | ||||
| n = 54 | Σ dp = –13 |
| M = 73 + | –13х3 | = 73–0,7 = 72,3 (ударов в минуту) |
Таким образом, полученное значение средней арифметической величины по способу моментов идентично таковому, найденному обычным способом.
Источник
Способ расчета средней арифметической величины
Тема 5: Средние величины
5.1 Сущность средних величин
5.2 Виды средних величин и способы их расчета
5.3 Математические свойства средней арифметической. Упрощеный метод расчета средней арифметической.
5.4 Структурные средние
5.5 Показатели вариации.
5.1.Сущность средних величин.
Средняя величина – это обобщающий количественный показатель, характеризующий типичный уровень совокупности по определенному признаку. Средняя величина является наиболее распространеной формой статистических показателей, используемых в экономических исследованиях.
Основные черты средней величины, как типичной характеристики явления:
1.Средняя величина отражает то общее, что присуще всем единицам исследуемой совокупности.
2. Средняя величина представляет значения оприделенного признака совокупности одним числом, несмотря на количественные различия у отдельных единиц совокупности.
3. Средняя величина абстрагируется от индивидуальных значений признака отдельных единиц совокупности и отражает то общее, что содержится в каждом отдельном единичном.
4. Средние величины тесно связаны с законом больших чисел.
5.2. Виды средних величин и способы их расчета
Виды средних величин:
1) Самый распространенный вид средней величины — это средняя арифметическая.
В общем случае ее расчет сводится к суммированию всех значений варьирующего признака и делению полученной суммы на количество единиц совокупности.
Средняя арифметическая может быть:
а) средняя арифметическая простая
xi — варианты осередняемого признака
n— число единиц совокупности
Средняя арифметическая простая применяется в тех случаях, когда значение каждого варианта встречается по одному разу
б) В тех случаях, когда значение вариантов встречаются несколько раз, для расчет применяют среднюю арифметическую взвешанную.
fi — частота этих вариантов.
В случае определения средней величины в интервальном ряду распределения сначала переходят от интервального к дискретному ряду, т.е. находят середину интервалов в каждой группе, как полусумму нижней и верхней границ в каждой группе.
2) Средняя гармоническая применяется в тех случаях, когда известны варианты осередняемого признака (xi) и показатели, представляющие произведение вариантов на частоты или веса средней арифметич.
Это произведение x*f=F и служит в качестве весов или частот средней гармонической.
Средняя гармоническая может быть простой и взвешанной.
а) средняя гармоническая простая
xi — варианты осередняемого признака
n— число вариантов осередняемого признака
Средняя гармоническая простая применятся в тех случаях, когда веса всех вариантов равны. В тех случаях, когда веса не равны, применяется средняя гармоническая взвешанная.
б) средняя гармоническая взвешанная
Средняя гармоническая — это средняя из обратных величин, поэтому ее применяют для расчета средней трудоемксти, которая является обратной величиной производительности труда (выработки).
На практике чаще всего применяются средняя арифметическая и средняя гармоническая. Чтобы правильно выбрать формулу средней, необходимо руководствоваться следующими правилами:
1. Средняя гармоническая применяется для расчета в тех случаях, когда показатеь, величина которого не известна находится в знаменателе исходного отношения (это экономическое содержание расчитываемое показателем)
ЗП=ФондЗП/ЧР
2. Если в искомом отношении не известен числитель, то для расчета применяют среднюю арифметическую взвешенную.
3) Средняя геометрическая применяется в тех случаях, когда определяемый показатель является не суммой значения признака, а их произведением, т.е. во всех случаях, где варианты связаны между собой не знаком «+», а знаком «*» расчитывают не среднюю арифметическую, а среднюю геометрическую. Средняя гармоническая бывает простая и взвешанная.
а) средняя геометрическая простая
xi — варианты осередняемого признака; n— число вариантов осередняемого признака
Применяется, когда варианты встречаются по одному разу.
В тех случаях, когда разное число вариантов, применяется
б) средняя геометрическая взвешенная
Ср. геом. простая применяется в экономических исследованиях для расчета среднего коэффициента роста. Ср. геом. взвешенная применяется для расчета средних величин, когда значения признака заключены в групповые интервалы. В этих случаях в качестве значения признака необходимо брать не значение их середины интервала, а log их полусуммы.
4) Средняя квадратичная применяется при осереднении величин, выраженных в виде квадратичной функции.
Применяется, когда варианты встречаются по одному разу. Применяется на практике редко. Ее используют в основном для расчета средних диаметров труб, средних сторон квадрата.
Между перечисленными средними величинами, рассчитанными по одной и той же совокупности единиц и по одному и тому же признаку существует следующая взаимосвязь:
5) Средняя хронологическая применяется для расчета средних величин в моментных рядах, когда значения признака представлены в хронологическом порядке через равные промежутки времени.
5.3 Математические свойства средней арифметической. Упрощеный метод расчета средней арифметической.
Определение средней арифметической в ряде случаев связано (при очень большой численности совокупности) с большими затратами времени и средств. Однако процедуру расчета средней можно упростить, если использовать некоторые ее свойства. Приведем без доказательства основные свойства средней арифметической:
1) средняя арифметическая от постоянной величины равна ей самой
2) произведение средней на сумму частот равно сумме произведения вариантов на их частоты
3) изменение каждого варианта на одно и тоже число и на одну и ту же величину изменяет среднюю на ту же величину
4) изменение каждого из весов (частот) в одно и тоже число раз не меняет величины средней
5) изменение каждого варианта в одно и тоже число раз изменяет среднюю во столько же раз
6) сумма отклонений каждого варианта от их средней равна нулю
7) средняя суммы равна сумме средних величин
Рассмотренные свойства средней арифметической используются для упрощения расчетов связанных с вычислением средней величины.
Метод упрощения вычисления средней арифметической называется методом условных моментов или методом отчета от условного нуля.
Согласно этому методу средняя рассчитывается по следующей формуле.
x0 – значение условного нуля
h – ширина интервала
m1 – условный момент первого порядка
Расчет средней арифметической способом условных моментов применяется для расчета средних в интервальных вариационных рядах.
5.4 Структурные средние.
В статистическом анализе кроме рассмотренных средних используют величины конкретных вариантов, которые занимают в упорядоченном ряду значений признака определенное положение. Это мода, медиана, квартири, децили, процентили. Эти средние называют структурными средними.
1) Медиана — это вариант расположенный в центре ранжированного ряда. Медиана делит ряд на две равные части, таким образом, что у одной половины единиц совокупности значения варьирующего признака меньше медианы, а у другой — больше.
Рассмотрим расчет медианы в вариационных рядах (дискретный и интервальный).
а) В дискретном вариационном ряду с четном числом вариантов медиана рассчитывается как среднее значение двух вариантов, имеющие порядковые номера n/2 и n/2+1.
В этих рядах с нечетным числом членов медиана рассчитывается по формуле n+1/2
б) В интервальных рядах медиана начинается с определения интервала, в котором находится медиана. Этот интервал называется медианный интервал. Этот интервал характерен тем, что его кумулятивная частота (сумма накопленных частот) равна или превышает полусумму всех частот ряда. После того, как нашли медианный интервал, значение медианы рассчитывается по следующей формуле:
XME – нижняя граница медианного интервала
h – ширина медианного интервала
SME-1 – кумулятивная частота, накопленная до медианного интервала.
2) Мода – это вариант, который чаще всего встречается в данной совокупности. Рассмотрим расчет моды в вариационных рядах:
а) В дискретном вариационом ряду модой является вариант обладающий наибольшей частотой.
б) в интервальном вариационном ряду расчет моды осуществляется в следующем порядке:
1. определяем модальный интервал, т.е. интервал обладающей наибольшей частотой;
2. производим расчет моды по формуле
XM0 – нижняя граница модального интервала
h – ширина модального интервала
fM0 – частота модального интервала
fM0-1 – частота предмодального интервала
fM0+1 – частота послемодального интервала
3) Наряду с медианой для полной характеристики изучаемой совокупности применяют:
а) квартири — делят ряд на 4-е равные части, из будет 3.
б) децили — делят ряд на 10 равных частей, их будет 9.
в) процентили — делят ряд на 100 равных частей, их будет 99
5.5 Показатели вариации.
Вариация – это такие количественные изменения величины исследуемого признака в пределах статистической совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов.
Например: размер зарплаты рабочих зависит от ряда факторов (специальность, разряд, стаж работы). Чем больше различия между значениями указанных факторов, тем больше вариаций в уровне заработной платы рабочих. Для характеристики вариации используют абсолютные и относительные показатели вариации.
1) Абсолютные (размах вариации) показатели – R – рассчитывается, как разница (..).
Чем меньше значение этого показателя, тем совокупность однороднее. Недостаток этого показателя в том, что он не учитывает изменения значений признака внутри предельных значений вариантов.
Вместе с тем для характеристики вариации признака необходимо знать не только размах предельных значений отклонений но и уметь обобщить отклонения всех значений от какой-либо типичной для изучаемой совокупности величины(средней). Такую характеристику вариаций дает среднее линейное отклонение.
Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их средней арифметической.
— это невзвешенное среднее линейное уравнение.
Применяется для вариационного ряда с равными частотами.
— это взвешенное.
Дисперсия — это средний квадрат отклонений вариантов от их средней арифметической.
— это простая дисперсия, которая применяется для в вариационных рядах с равными частотами.
В вариационных рядах с неравными частотами рассчитывают дисперсию взвешенную.
Для интервальных вариационных рядов с равными интервалами дисперсия рассчитывается способом условных моментов.
h – ширина интервала
m1 – условный момент 1-го порядка
m2 – условный момент второго порядка
2) Относительные показатели.
В статистической практике часто возникает необходимость сравнения вариации различных признаков. Например, сравнение вариации возраста рабочих и их квалификации, стажа работы и размера из з/п. Для таких сопоставлений абсолютные показатели вариации нельзя и использовать, тюк нельзя сравнивать вариацию стажа работы, выраженного в годах с вариацией з/п, выраженной в леях. Для таких сравнений используют относительный показатель вариации, который наз-ся коэффициентом вариации.
Коэффициент вариации применяется не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Если к.в. меньше 30 %, то совокупность является однородной.
Источник