Способ расчета относительных величин сравнения
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2
Расчёт относительных величин.
— область применения и методику расчёта относительных величин .
— исчислять относительные величины;
— формулировать вывод по полученным результатам.
Относительные величины дают качественную характеристику изучаемых явлений. Это числовые показатели, представляющие собой соотношение двух сопоставляемых одноимённых абсолютных величин. В статистике исчисляют следующие относительные величины:
1) относительная величина планового задания ( ОВпл .з ад .) рассчитывается как отношение уровня, запланированного на предстоящий период, к уровню, фактически сложившемуся в предшествующем периоде;
2) относительная величина выполнения планового задания ( ОВвып .п л,зад .) рассчитывается как отношение фактически достигнутого в данном периоде уровня к запланированному уровню;
3) относительная величина динамики (ОВ дин) характеризует развитие изучаемого явления во времени, рассчитывается делением уровня признака в определённый период или момент времени на уровень этого признака в предшествующий период или момент времени; исчисляется в виде темпа роста в форме коэффициента или процента;
Например: Пусть имеются значения показателя Х за два периода
Базисный (предыдущий) период
Отчетный (текущий) период
относительная величина планового задания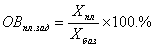 
относительная величина выполнения планового задания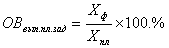 
относительная величина динамики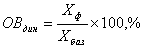 
Между относительными величинами планового задания, выполнения планового задания и динамики существует следующая взаимосвязь:
.
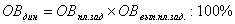
Основываясь на этой взаимосвязи по любым двум известным величинам можно определить третью неизвестную величину.
4) относительные величины структуры характеризуют доли или удельные веса частей изучаемого явления во всей совокупности;
Например: если явление Х можно представить как сумму его частей а, в и с,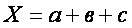 
, то:
относительная величина структуры части а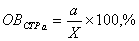 
;
относительная величина структуры части в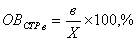 
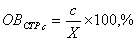
; относительная величина структуры части с 
;
сумма относительных величин структуры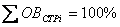 
Или же доля части а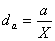 
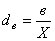
; доля части в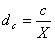 
;
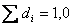
доля части с 
; сумма долей 
5) относительные величины интенсивности характеризуют степень распределения или развития данного явления в той или иной среде; представляют собой отношение абсолютного уровня одного показателя, свойственного изучаемой среде, к другому абсолютному показателю, также присущему данной среде и, как правило, являющемуся для первого показателя факторным признаком (например, при изучении демографических процессов рассчитываются показатели рождаемости или смертности, как отношение числа родившихся (или умерших) к среднегодовой численности населения данной территории;
Имеются следующие данные по стране «А» за 2009 г .;
Число родившихся, тыс. чел…………………………… 5611
Среднегодовая численность населения, млн. чел ……. 280,25
Определите относительную величину интенсивности, характеризующую рождаемость в стране «А».
Для решения задачи необходимо определить коэффициент рождаемости в стране «А» за 2009г.
(промилле)
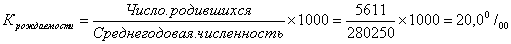
Этот показатель свидетельствует о том, что рождаемость в стране «А» в расчете на каждую 1000 чел. населения составляла в 2009 году 20 чел.
Примерами относительных величин интенсивности являются показатели уровня технического развития производства, уровня благосостояния граждан, показатели обеспеченности населения средствами массовой информации, предметами культурно-бытового назначения и т.д. Относительная величина интенсивности рассчитывается по формуле:
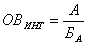
где А — распространение явления; БА — среда распространения явления А.
При расчете относительных величин интенсивности может возникнуть проблема выбора адекватной явлению базы сравнения (среды распространения явления). Например, при определении показателя плотности населения нельзя брать в качестве базы сравнения общий размер территории того или иного государства, в этом случае базой сравнения может быть лишь территория в 1 км 2 . Критерием правильности расчета является сопоставимость по разработанной методологии расчета сравниваемых показателей, применяющихся в статистической практике.
6) относительные величины координации характеризуют отношение частей данной совокупности к одной из них, принятой за базу сравнения, и показывают, во сколько раз одна часть совокупности больше другой, либо сколько единиц одной части приходится на 1, 10, 100, 1000 единиц другой части.
Имеются данные о среднегодовой численности рабочих и служащих в промышленности региона 2009 г . (млн. чел):
Всего рабочих и служащих …………………………………………….10,9
рабочих, включая обслуживающий персонал и работников охраны…..7,6
Исчислите, сколько служащих приходится на 100 рабочих
Относительные величины координации исчисляют соотношением частей целого. Поэтому относительная величина координации будет определена так:
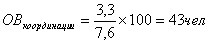
Следовательно, на каждые 100 рабочих (включая младший обслуживающий персонал и работников охраны) в промышленности района в 2009 г . приходится 43 служащих.
1) относительные величины сравнения характеризуют сравнительные размеры одноимённых абсолютных величин, относящихся к одному и тому же периоду или моменту времени, но к различным объектам или территориям.
Число квартир, построенных на каждые 10000 чел населения в стране «А» и стране «Б» в 2009 г ., характеризуется следующими данными:
страна «А» — 75, страна «Б» — 71.
Сравните число квартир, построенных на каждые 10000 чел населения в стране «А» и в стране «Б».
Относительная величина сравнения будет исчислена отношением исходных данных о числе квартир, построенных на каждые 10000 чел населения:
т.е. в 2009 г . по числу построенных квартир на каждые 10000 чел населения страна «А» превосходила страну «Б» в 1,056 раза.
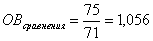
Вывод: Относительная величина в статистике выступает в качестве обобщающего показателя, который дает числовую меру соотношения двух сопоставляемых абсолютных величин. Так как многие абсолютные величины взаимосвязаны, то и относительные величины одного типа в ряде случаев могут определяться через относительные величины другого типа.
Основное условие правильного расчета относительной величины – сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями. Таким образом, по способу получения относительные показатели – всегда величины производные, определяемые в форме коэффициентов, процентов, промилле, продецимилле и т.п. Однако нужно помнить, что этим безразмерным по форме показателям может быть, в сущности, приписана конкретная, и иногда довольно сложная, единица измерения. Так, например, относительные показатели естественного движения населения, такие как коэффициенты рождаемости или смертности, исчисляемые в промилле (‰), показывают число родившихся или умерших за год в расчете на 1000 человек среднегодовой численности; относительная величина эффективности использования рабочего времени – это количество продукции в расчете на один отработанный человеко-час и т.д.
Источник
Относительная величина (относительный показатель) сравнения, координации, интенсивности
Следующий вид относительных величин – это относительная величина сравнения или как еще ее называют относительный показатель сравнения. По своему статусу величина сравнения занимает, скорее всего, пятое место среди всех относительных величин, после величин динамики, выполнения плана, планового задания и структуры. А вот по частоте использования, пожалуй, первое. Кроме того в этой части мы рассмотрим еще две относительные величины, которые также могут быть использованы в аналитических целях.
Относительная величина сравнения
Дело все в том, что относительная величина сравнения проводит сравнение одного показателя с другим. Получаем, что показатель сравнения это и есть сама относительная величина. Что такое относительные величины и как она рассчитывается можно посмотреть в этой лекции.
Относительная величина сравнения характеризует сравнительные размеры разных объектов или абсолютных величин, но отнесенных к одному и тому же явлению. Например, пакет молоко объемом 1 литр в одном магазине стоит 50 рублей, а в другом 60 рублей, то мы можем сравнить их стоимость, и выявить во сколько раз один стоит дороже другого. 60 : 50 = 1,2. То есть пакет молока во втором магазине стоит в 1,2 раза дороже.
Таким нехитрым действие и рассчитываются относительные величины сравнения, причем процесс расчета может состоять не из одного действия, а сразу из нескольких. Если в качестве сравниваемых величин будут использоваться несколько объектов, а база сравнения естественно будет одна.
Учитывая вышесказанное определить относительную величину сравнения (ОВСр) можно по следующей формуле
В данном случае, как и в любой относительной величине в числителе (сверху) находится сравниваемая величина, а в знаменателе (внизу) базисная величина. Базисная величина может меняться в зависимости от задания и целей расчета. Например, имеет данные о производстве мяса в Московской области, Тульской области, Брянской области, Смоленской области. Если за базу сравнения взять область Московскую, то все данные по другим областям мы будем делить на данные по Московской области. Если же за базу сравнения мы возьмем Тульскую, то, следовательно, данные по всем другим областям мы поделим на данные по Тульской области.
Пример. Имеются условные данные о производстве молока в четырех областях. Рассчитайте относительный показатель сравнения, приняв за базу сравнения данные по Московской области, а затем данные по Тульской области.
Кроме сравнения с данным по Московской и Тульской областям, аналогично можно производить сравнение с данными по Смоленской и Брянской областям. Все зависит от целей сравнения.
Кроме рассмотренных пяти относительных величин в статистике также используются еще две разновидности. Используются они реже, чем основные, но также достойны внимания.
Относительная величина координации
Относительный показатель координации используется в основном в узко аналитических целях. Для сравнения частей внутри статистической совокупности.
Относительная величина координации показывает соотношение частей целого между собой. Это базовое определение данной относительной величины.
Величина координации похожа на относительную величину структуры. Только если в структуре мы части делили на целое, то здесь часть будет делиться на другую часть, которую выбрали за базу сравнения.
Получаем соотношение основных базовых частей друг с другом, которые используются для конкретных целей анализа.
Формула расчет относительной величины координации (ОВК) имеет вид:
Возможны и другие варианты частей, например 3 с 1 и так далее.
Относительная величина интенсивности развития
Величина интенсивности показывает степень развития какого-то показателя в какой-то среде. Способ расчета показателя интенсивности классический, и похож на расчет величины сравнения.
Часто величина интенсивности рассчитывается в процентах, промиллях.
Обычно используется в статистике населения для характеристики демографических показателей. Например, уровней рождаемости.
Число родившихся в городе составило 15 человек на каждую тысячу живущих. Это и есть пример величины интенсивности развития.
Кроме того такой способ расчета используется и в экономике организации. Фондовооруженность показатель характеризующий величину основных фондов приходящихся на одного работника.
Чтобы вернуться к списку лекций нажмите на ссылку.
Источник
Способ расчета относительных величин сравнения
4.2 пФОПУЙФЕМШОЩЕ РПЛБЪБФЕМЙ
бОБМЙЪ — ЬФП, РТЕЦДЕ ЧУЕЗП, УТБЧОЕОЙЕ, УПРПУФБЧМЕОЙЕ УФБФЙУФЙЮЕУЛЙИ ДБООЩИ. ч ТЕЪХМШФБФЕ УТБЧОЕОЙС РПМХЮБАФ ЛБЮЕУФЧЕООХА ПГЕОЛХ ЬЛПОПНЙЮЕУЛЙИ СЧМЕОЙК, ЛПФПТБС ЧЩТБЦБЕФУС Ч ЧЙДЕ ПФОПУЙФЕМШОЩИ ЧЕМЙЮЙО.
пФОПУЙФЕМШОЩЕ ЧЕМЙЮЙОЩ РТЕДУФБЧМСАФ ЮБУФОПЕ ПФ ДЕМЕОЙС ДЧХИ УФБФЙУФЙЮЕУЛЙИ ЧЕМЙЮЙО Й ИБТБЛФЕТЙЪХАФ ЛПМЙЮЕУФЧЕООПЕ УППФОПЫЕОЙЕ НЕЦДХ ОЙНЙ.
рТЙ ТБУЮЕФЕ ПФОПУЙФЕМШОЩИ ЧЕМЙЮЙО Ч ЮЙУМЙФЕМЕ ЧУЕЗДБ ОБИПДЙФУС УТБЧОЙЧБЕНЩК РПЛБЪБФЕМШ, Б Ч ЪОБНЕОБФЕМЕ РПЛБЪБФЕМШ, РТЙОЙНБЕНЩК ЪБ ВБЪХ ДМС УТБЧОЕОЙС.
ч ЪБЧЙУЙНПУФЙ ПФ ФПЗП, ЛБЛПЕ ЮЙУМПЧПЕ ЪОБЮЕОЙЕ ЙНЕЕФ ВБЪБ УТБЧОЕОЙС (ЪОБНЕОБФЕМШ), ТЕЪХМШФБФ ПФОПЫЕОЙС НПЦЕФ ВЩФШ ЧЩТБЦЕО Ч ЖПТНЕ ЛПЬЖЖЙГЙЕОФБ, РТПГЕОФБ, РТПНЙММЕ Й РТПДЕГЙНЙММЕ. еУМЙ ВБЪБ УТБЧОЕОЙС РТЙОЙНБЕФУС ЪБ 1, ФП ПФОПУЙФЕМШОЩК РПЛБЪБФЕМШ ЧЩТБЦБЕФУС Ч ЛПЬЖЖЙГЙЕОФБИ, ЕУМЙ ВБЪБ УТБЧОЕОЙС РТЙОЙНБЕФУС ЪБ 100, 1000 ЙМЙ 10000, ФП ПФОПУЙФЕМШОЩК РПЛБЪБФЕМШ УППФЧЕФУФЧЕООП ЧЩТБЦБЕФУС Ч РТПГЕОФБИ ( o / o ), РТПНЙММЕ ( o / oo ), РТПДЕГЙНЙММЕ ( o / ooo ).
чУЕ ЙУРПМШЪХЕНЩЕ ОБ РТБЛФЙЛЕ ПФОПУЙФЕМШОЩЕ УФБФЙУФЙЮЕУЛЙЕ РПЛБЪБФЕМЙ НПЦОП РПДТБЪДЕМЙФШ ОБ УМЕДХАЭЙЕ ЧЙДЩ:
ћ РПЛБЪБФЕМЙ ДЙОБНЙЛЙ;
ћ РПЛБЪБФЕМЙ РМБОБ Й ТЕБМЙЪБГЙЙ РМБОБ;
ћ РПЛБЪБФЕМЙ УФТХЛФХТЩ;
ћ РПЛБЪБФЕМЙ ЛППТДЙОБГЙЙ;
ћ РПЛБЪБФЕМЙ ЙОФЕОУЙЧОПУФЙ;
ћ РПЛБЪБФЕМЙ УТБЧОЕОЙС.
пФОПУЙФЕМШОЩК РПЛБЪБФЕМШ ДЙОБНЙЛЙ (прд) РТЕДУФБЧМСЕФ ПФОПЫЕОЙЕ ХТПЧОС ЙУУМЕДХЕНПЗП РТПГЕУУБ ЙМЙ СЧМЕОЙС ЪБ ДБООЩК РЕТЙПД ЧТЕНЕОЙ Й ХТПЧОС ЬФПЗП ЦЕ РТПГЕУУБ ЙМЙ СЧМЕОЙС Ч РТПЫМПН.
 | (4.1) |
тБУУЮЙФБООБС ФБЛЙН ПВТБЪПН ЧЕМЙЮЙОБ РПЛБЪЩЧБЕФ, ЧП УЛПМШЛП ТБЪ ФЕЛХЭЙК ХТПЧЕОШ ЙЪНЕОЙМУС РП ПФОПЫЕОЙА Л РТЕДЫЕУФЧХАЭЕНХ (ВБЪЙУОПНХ). тБУЮЕФ прд ЧЩРПМОСЕФУС Ч ЧЙДЕ ФЕНРПЧ ТПУФБ, РТЙТПУФБ Й ДТ. рТЙ ОБМЙЮЙЙ ДБООЩИ ЪБ ОЕУЛПМШЛП РЕТЙПДПЧ ЧТЕНЕОЙ УТБЧОЕОЙЕ ЛБЦДПЗП ДБООПЗП ХТПЧОС НПЦЕФ РТПЙЪЧПДЙФШУС МЙВП У ХТПЧОЕН РТЕДЫЕУФЧХАЭЕЗП РЕТЙПДБ, МЙВП У ДТХЗЙН, РТЙОСФЩН ЪБ ВБЪХ. ч РЕТЧПН УМХЮБЕ РПМХЮБАФУС ГЕРОЩЕ РПЛБЪБФЕМЙ ДЙОБНЙЛЙ, ЧП ЧФПТПН — ВБЪЙУОЩЕ.
рТЙНЕТ: РТПЙЪЧПДУФЧП НСУБ Ч тж Ч 1994-1997 З.З. ИБТБЛФЕТЙЪХЕФУС УМЕДХАЭЙНЙ ДБООЩНЙ:
| зПД | 1994 | 1995 | 1996 | 1997 |
| пВЯЕН РТПЙЪЧПДУФЧБ, ФЩУ.Ф | 81,7 | 70,0 | 48,2 | 38,0 |
тБУУЮЙФБЕН ПФОПУЙФЕМШОЩЕ РПЛБЪБФЕМЙ ДЙОБНЙЛЙ У РЕТЕНЕООПК Й РПУФПСООПК ВБЪБНЙ УТБЧОЕОЙС:
| рЕТЕНЕООБС ВБЪБ УТБЧОЕОЙС (ГЕРОЩЕ РПЛБЪБФЕМЙ) | рПУФПСООБС ВБЪБ УТБЧОЕОЙС (ВБЪЙУОЩЕ РПЛБЪБФЕМЙ) |
| 70:87,1 ћ 100% = 80,4% | 70:87,1 ћ 100% = 80,4% |
| 48,2:70 ћ 100% = 68,9% | 48,2:87,1 ћ 100% = 55,3% |
| 38,0:48,2 ћ 100% = 78,8% | 38,0:87,1 ћ 100% = 43,6% |
пФОПУЙФЕМШОЩЕ РПЛБЪБФЕМЙ ДЙОБНЙЛЙ У РЕТЕНЕООПК Й РПУФПСООПК ВБЪПК УТБЧОЕОЙС ЧЪБЙНПУЧСЪБОЩ НЕЦДХ УПВПК УМЕДХАЭЙН ПВТБЪПН: РТПЙЪЧЕДЕОЙЕ ЧУЕИ ПФОПУЙФЕМШОЩИ РПЛБЪБФЕМЕК У РЕТЕНЕООПК ВБЪПК ТБЧОП ПФОПУЙФЕМШОПНХ РПЛБЪБФЕМА У РПУФПСООПК ВБЪПК ЪБ ЙУУМЕДХЕНЩК РЕТЙПД. фБЛ, ДМС ТБУУЮЙФБООЩИ РПЛБЪБФЕМЕК (РТЕДЧБТЙФЕМШОП РЕТЕЧЕДС ЙЪ РТПГЕОФПЧ Ч ЛПЬЖЖЙГЙЕОФЩ):
0,804 ћ 0,689 ћ 0,788 = 0,436 ЙМЙ 43,6%
уМЕДХАЭЙЕ ПФОПУЙФЕМШОЩЕ РПЛБЪБФЕМЙ: ПФОПУЙФЕМШОЩК РПЛБЪБФЕМШ РМБОБ (прр) Й ТЕБМЙЪБГЙЙ РМБОБ (пртр).
 | (4.2) |
 | (4.3) |
прр РПЛБЪЩЧБЕФ ЧП УЛПМШЛП ТБЪ ОБНЕЮБЕНЩК ПВЯЕН РТПЙЪЧПДУФЧБ РТЕЧЩУЙФ ДПУФЙЗОХФЩК ХТПЧЕОШ.
рТЙНЕТ: РМБОЙТПЧБМПУШ Ч 1999 З. ОБ НПМПЛПРЕТЕТБВБФЩЧБАЭЕН ЪБЧПДЕ РЕТЕТБВПФБФШ 150 Ф. НПМПЛБ. жБЛФЙЮЕУЛЙ РЕТЕТБВПФБМЙ ЪБ 1998 З. 120 Ф. ч ЬФПН УМХЮБЕ ПФОПУЙФЕМШОЩК РПЛБЪБФЕМШ РМБОБ УПУФБЧЙФ 125% (150 : 120 ћ 100). рТЕДРПМПЦЙН, ЮФП ЖБЛФЙЮЕУЛЙК ПВЯЕН РЕТЕТБВПФЛЙ НПМПЛБ Ч 1999 З. УПУФБЧЙМ 110 Ф. фПЗДБ, ПФОПУЙФЕМШОЩК РПЛБЪБФЕМШ ТЕБМЙЪБГЙЙ РМБОБ УПУФБЧЙФ 73,3% (110 : 150 ћ 100).
пФОПУЙФЕМШОЩК РПЛБЪБФЕМШ УФТХЛФХТЩ (пру) ИБТБЛФЕТЙЪХЕФ УПУФБЧ ЙЪХЮБЕНЩИ УПЧПЛХРОПУФЕК (ДБЕФ РТЕДУФБЧМЕОЙЕ П ДПМЙ ПФДЕМШОЩИ СЧМЕОЙК ЧП ЧУЕК УПЧПЛХРОПУФЙ). рПМХЮБАФ ЕЗП РХФЕН УПРПУФБЧМЕОЙС ЮБУФЙ У ГЕМЩН. чЩТБЦБЕФУС Ч % Й ЛПЬЖЖЙГЙЕОФБИ.
 | (4.4) |
рТЙНЕТ: РТПЖЕУУПТУЛП-РТЕРПДБЧБФЕМШУЛЙК УПУФБЧ чхъБ ИБТБЛФЕТЙЪХЕФУС УМЕДХАЭЙНЙ ДБООЩНЙ:
| лБФЕЗПТЙЙ | юЙУМП, ЮЕМ. | уФТХЛФХТБ, % |
| рТПЖЕУУПТБ | 50 | 11,1 (50 : 450) ћ 100 |
| дПГЕОФЩ | 120 | 26,7 (120 : 450) ћ 100 |
| уФ. РТЕРПДБЧБФЕМЙ | 180 | 40,0 (180 : 450) ћ 100 |
| бУУЙУФЕОФЩ | 100 | 22,2 (100 : 450) ћ 100 |
| йфпзп | 450 | 100 |
тБУУЮЙФБООЩЕ Ч РПУМЕДОЕК ЗТБЖЕ ФБВМЙГЩ РТПГЕОФЩ РТЕДУФБЧМСАФ УПВПК ПФОПУЙФЕМШОЩЕ РПЛБЪБФЕМЙ УФТХЛФХТЩ.
пФОПУЙФЕМШОЩК РПЛБЪБФЕМШ ЛППТДЙОБГЙЙ (прл) РТЕДУФБЧМСЕФ УПВПК ПФОПЫЕОЙЕ ПДОПК ЮБУФЙ УПЧПЛХРОПУФЙ Л ДТХЗПК ЮБУФЙ ЬФПК ЦЕ УПЧПЛХРОПУФЙ:
 | (4.5) |
ч ЛБЮЕУФЧЕ ВБЪЩ УТБЧОЕОЙС ЧЩВЙТБЕФУС ФБ ЮБУФШ, ЛПФПТБС ЙНЕЕФ ОБЙВПМШЫЙК ХДЕМШОЩК ЧЕУ Й СЧМСЕФУС ПУОПЧПК У ЬЛПОПНЙЮЕУЛПК, УПГЙБМШОПК ЙМЙ ДТХЗПК ФПЮЛЙ ЪТЕОЙС.
фБЛ, ОБ ПУОПЧЕ ДБООЩИ РТЕДЩДХЭЕЗП РТЙНЕТБ НЩ НПЦЕН ЧЩЮЙУМЙФШ, ЮФП ОБ ЛБЦДПЗП УФБТЫЕЗП РТЕРПДБЧБФЕМС РТЙИПДЙФУС 0,27 РТПЖЕУУПТБ, 0,67 ДПГЕОФБ Й 0,56 БУУЙУФЕОФБ.
пФОПУЙФЕМШОЩК РПЛБЪБФЕМШ ЙОФЕОУЙЧОПУФЙ (прй) ИБТБЛФЕТЙЪХЕФ УФЕРЕОШ ТБУРТПУФТБОЕОЙС ЙЪХЮБЕНПЗП РТПГЕУУБ ЙМЙ СЧМЕОЙС. пО РПЛБЪЩЧБЕФ УППФОПЫЕОЙЕ ТБЪОПЙНЕООЩИ, ОП УЧСЪБООЩИ НЕЦДХ УПВПК БВУПМАФОЩИ ЧЕМЙЮЙО. ч ПФМЙЮЙЕ ПФ ДТХЗЙИ ЧЙДПЧ ЧЕМЙЮЙО, ПОЙ ЧУЕЗДБ ЧЩТБЦБАФУС ЙНЕОПЧБООЩНЙ ЧЕМЙЮЙОБНЙ.
 | (4.6) |
рТЙНЕТПН прй НПЦЕФ УМХЦЙФШ РПЛБЪБФЕМШ, ИБТБЛФЕТЙЪХАЭЙК ЮЙУМП НБЗБЪЙОПЧ РП 10000 ЮЕМПЧЕЛ ОБУЕМЕОЙС. пО РПМХЮБЕФУС ДЕМЕОЙЕН ЮЙУМБ НБЗБЪЙОПЧ Ч ТЕЗЙПОЕ ОБ ЮЙУМЕООПУФШ ОБУЕМЕОЙС ТЕЗЙПОБ.
тБЪОПЧЙДОПУФША прй СЧМСЕФУС ПФОПУЙФЕМШОЩЕ РПЛБЪБФЕМЙ ХТПЧОС ЬЛПОПНЙЮЕУЛПЗП ТБЪЧЙФЙС, ИБТБЛФЕТЙЪХАЭЙЕ РТПЙЪЧПДУФЧП РТПДХЛГЙЙ Ч ТБУЮЕФЕ ОБ ДХЫХ ОБУЕМЕОЙС Й ЙЗТБАЭЙЕ ЧБЦОХА ТПМШ Ч ПГЕОЛЕ ТБЪЧЙФЙС ЬЛПОПНЙЛЙ ЗПУХДБТУФЧБ.
пФОПУЙФЕМШОЩК РПЛБЪБФЕМШ УТБЧОЕОЙС (пруТ) ИБТБЛФЕТЙЪХЕФ ЛПМЙЮЕУФЧЕООПЕ УППФОПЫЕОЙЕ ПДОПЙНЕООЩИ РПЛБЪБФЕМЕК, ПФОПУСЭЙИУС Л ТБЪМЙЮОЩН ПВЯЕЛФБН УФБФЙУФЙЮЕУЛПЗП ОБВМАДЕОЙС. оБРТЙНЕТ, ЮЙУМЕООПУФШ ЦЙФЕМЕК нПУЛЧЩ Й пТЕОВХТЗБ, ГЕОЩ ОБ ТЩОЛЕ Й Ч НБЗБЪЙОЕ.
Источник
