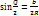ДЕТАЛЬНАЯ РАЗБИВКА КРУГОВЫХ КРИВЫХ
Детальная разбивка кривой предусматривает не только закреп-ление на местности начала НК, конца КК и середины СК кривой, но и обозначение всей кривой, например, колышками через определен-ный интервал. Существует ряд способов разбивки круговых кривых: способ прямоугольных координат, способ углов, способ продолжен-ных хорд.
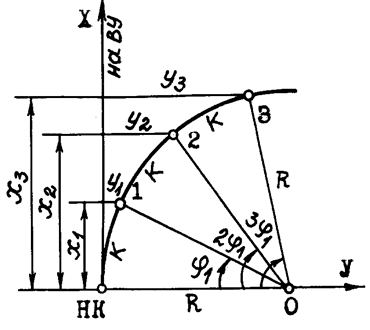
Способ прямоугольных координат (ординат от тангенса).
|
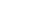


|
|
|
|
|
|
В эти формулы подставляют значение угла j1, зависящее от величины интервала К, которое можно найти из выражения:
j1= 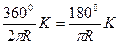
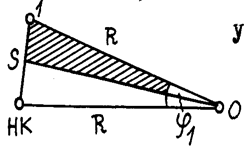
На местности откладывают от начала кривой НК по направ-лению на вершину угла поворота ВУ (по направлению тангенса) абсциссы Хi , а по перпендикулярному направлению ординаты Уi и закрепляют точки 1, 2, 3 и т.д. Так производят разбивку до середины кривой. Другую половину кривой разбивают с ее конца. Для определения координат Х и У существуют специальные таблицы.
Этот способ применяется на ровной площадке и является наиболее точным, так как точки 1, 2, 3 и т.д. выносят независимо друг от друга, поэтому ошибка положения одной точки не окажет влияния на положение других точек, чего нельзя сказать о рассмат-риваемых далее способах углов и продолженных хорд .
Способ углов (полярный способ).
|
|
|
|
|
Этот способ удобно применять в стесненных условиях, когда есть видимость между НК и точками 1, 2, 3. (например, на высокой насыпи, где способ прямоугольных координат неприемлем).
|
|

|
|
|
|
Способ продолженных хорд
|
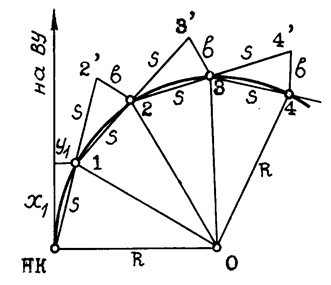
Вначале по координатам Х1 и У1 выносят точку 1. Затем в створе НК-1 на расстоянии S от точки 1 отмечают вспомогательную точку 2’, от которой откладывают так называемое промежуточное
|
|




|
|
Этим способом одну половину кривой разбивают с HK, а дру-гую половину — с конца кривой КК. Способ применим в любыхстес-ненных условиях, в том числе и в выемке, где первые два способа неприемлемы.
Недостатком способов углов и продолженных хорд является снижение точности разбивки кривой по мере возрастания ее длины, так как положение каждой последующей точки определяется относительно предыдущей.
Источник
Детальная разбивка кругов. кривых: способ прямоугольных координат, способ проложенных хорд, способ углов
Способ прямоугольных координат
Порядок разбивки данным способом следующий.
1)Задавшись длиной дуги S (расстояние между соседними точками разбивки), приняв нк или кк за начало координат, направление тангенсов на вершину угла за направление оси Х, вычисляют координаты точек кривой по формулам
2) По φ и R определяют главные элементы кривой – Т (тангенс, касательная к кривой), Б (биссектриса), К (длина кривой), Д (домер).
3) Закрепляют главные точки кривой – нк, ск, кк.
Для этого от вершины угла при помощи рулетки по направлению к началу трассы откладывают Т. Полученная точка является нк и закрепляется деревянным колышком. Затем откладывают Т от ВУ по направлению на последующее направление трассы, получают, таким образом кк, которую тоже закрепляют колышком. Внутренний угол при помощи теодолита делят пополам и на полученном направлении откладывают Б, получают ск.φ – угол поворота трассы (в данном случае вправо); ВУ – вершина угла; нк – начало кривой; кк – конец кривой; ск – середина кривой. Эти точки называют главными точками кривой. R – радиус кривой.
у1=R-R·cosβ=R·(1-cosβ)=2R·sin 2 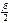
уn=2R·sin 2 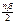
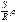

4) Вдоль тангенсов от нк и кк откладывают при помощи рулетки значения хn по перпендикуляру уn и закрепляют полученные точки колышками.
Способ продолженных хорд
Заключается в следующем :
1.По значению S и R вычисляют х1=Rsinβ; у1=2Rsin 2 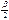
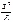
2.Точку 1 закрепляют колышком, отложив при помощи рулетки х1 от начала кривой по направлению на вершину угла (по оси Х) и у1 перпендикулярно этому направлению.
3.По точкам 0 – 1 натягивают ленту или рулетку и на продолжении 01 откладывают S, закрепляют точку 2′.
4.Точку 2 на кривой получают способом линейных засечек: пересечением отрезка S, который откладывают рулеткой из точки 1 и отрезка в, откладываемого из точки 2′. Полученную точку закрепляют деревянным колышком.
5.Таким же образом разбивают точки 3, 4, до середины кривой. Вторую половину кривой разбивают таким же образом от точки конца кривой.
Достоинство способа в том, что он применим на любой местности (косогоры, впадины и т.д.). Недостаток – с возрастанием длины кривой точность разбивки падает, так как положение последующей точки определяется относительно предыдущей. Происходит накопление ошибок.
В этом способе используется то положение, что углы с вершиной в какой-либо точке круговой кривой образован касательной АМ(Т) и соответствующей секущей равны половине соответствующего центрального угла. Данный способ заключается в построении угла q/2 в начале системы координат и последовательном откладывании хорды. При заданной длине хорды угол y определяют по формуле:
где в – длина хорды.
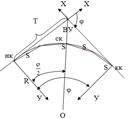
Для разбивки промежуточных точек кривой, теодолит устанавливают в НК или КК, ориентируют его по линии тангенса и откладывают от этой линии угол q/2 . Отложив вдоль построенного направления хорду l, закрепляют первую точку (В). Затем, в той же точке НК строят угол 2q/2 и откладывают хорду (В-С), получая на пересечении направления угла и хорды точку 2, и т.д. (рис. 179).
Линейные измерения выполняют вблизи кривой, что выгодно при разбивке точек на насыпи. Этот способ применяют для разбивки кривых земляных сооружений.
Порядок выполнения разбивки следующий:
— Выбирают из таблиц по радиусу угол Q/2 в зависимости от величины b (b=10,20,30 м).
— Устанавливают теодолит в точку А и от линии АМ фиксируют направление под углом Q/2.
— Вдоль этого направления откладывают длину хорды b и закрепляют на местности точку.
— Из точки А от направления АМ Фиксируют следующее направление под углом Q и вдоль него откладывают длину хорды. В такой последовательности выполняют разбивку всей кривой.
Источник
Детальная разбивка кривых
В качестве исходной информации задаются следующие данные:
1. Направление исходной трассы дороги.
2. Положение вершины угла поворота.
3. Значения угла и радиусаRповорота.
На первом этапе, по этим данным находят главные элементы кривой (длина кривой К, тангенсы Т, биссектриса Б, домер Д). Для этой цели используются известные формулы или таблицы детальной разбивки кривых.
Над вершиной угла устанавливается в рабочее положение теодолит и от направления исходной трассы откладывается заданный угол поворота и с помощью вешки фиксируется направление трассы дороги после поворота.
От вершины угла (ВУ) с помощью рулетки откладываются в переднем и заднем направлении отрезки, равные тангенсам, и с помощью колышков закрепляются точки начала кривой (НК) и конца кривой (КК).
С использованием известных значений угла поворота , вычисляется угол по формуле
Таким образом находится направление биссектрисы угла , которое фиксируется с помощью вехи. От вершины угла в этом направлении с помощью рулетки откладывается расстояние, равное биссектрисеБ, и колышком фиксируется точка середины кривой (СК).
На этом заканчивается разбивка основных элементов кривой и приступают к детальной разбивке, которая выполняется двумя способами:
1. Способом прямоугольных координат.
2. Способом продолженных хорд.
Способ прямоугольных координат
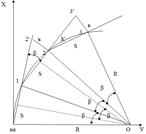
Направление НК – ВУ принимается за ось абсцисс, причем ее начало располагается в точке НК. Перпендикулярное направление от НК к центру условной окружности с радиусом Rпринимается за ось ординат (рис. 1.5).
Рис. 1.5. Схема к разбивке кривой способом прямоугольных координат
Координаты точки 1на кривой находятся по формуле:
Здесь 
Координаты точки 2находятся по формуле:
Таким же образом находятся координаты всех точек, лежащих на участке кривой от НК до СК.
Вторая часть кривой строится аналогично, но за ось абсцисс в этом случае принимается направление КК – ВУ, а за ось ординат принимается перпендикулярное направление от точки КК к центру условной окружности.
Критерием качества выполненной работы является точное схождение двух полученных частей кривой к точке СК.
Способ продолженных хорд
Выбор системы координат и определение положения точки 1производится аналогично предыдущему способу.
Далее, с помощью рулетки измеряется длина отрезка НК – 1(этот отрезок является хордойsэлементарной дуги кривойk) и по продолжению этой хорды откладывается отрезок такой же длиныs(рис. 1.6).
В результате получают вспомогательную точку 2. Окончательное положение точки2получают способом линейной засечки: от точки1откладывается дуга радиусомs, а от точки2дуга радиусом, вычисляемым по формуле
Далее с помощью рулетки измеряется расстояние от точки 1до точки2, продолжается на такое же расстояние, фиксируется вспомогательной точкой3, затем способом линейной засечки находится окончательное положение точки3.
Рис. 1.6. Схема к разбивке кривой способом продолженных хорд
Таким образом находится положение всех точек на участке кривой от НК до СК.
Вторая часть кривой строится аналогично от точки КК к точке СК. Критерием правильности построений является точное схождение двух частей кривой к точке СК.
Недостатком этого способа является возможное накопление ошибок.
Источник

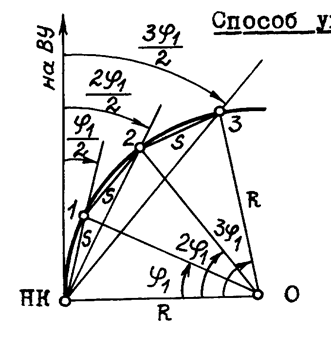
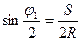 (из решения заштрихованного треугольника), причем в этом способе S явля-ется хордой определенной длины.
(из решения заштрихованного треугольника), причем в этом способе S явля-ется хордой определенной длины.