Способ прямоугольного проецирования придумал

Способ прямоугольного проецирования

Проекционное черчение (основы начертательной геометрии)

Метод проекций

Способ прямоугольного проецирования

Если проецирующие лучи составляют с плоскостью проекций прямой угол, то такие проекции называют прямоугольными.

Прямоугольные проекции называют также ортогональными. Слово «ортогональные» происходит от греческих слов «ortos» — прямой и «gonia» — угол.

Чертежи в системе прямоугольных проекций дают полное представление о форме и размерах предмета. Их легче выполнять, чем аксонометрические проекции.

Что нужно знать для успешного выполнения чертежей?

Всякий предмет, имеющий плоские поверхности, ограничивается вершинами, ребрами и гранями (рис. 108). Следовательно, чтобы научиться изображать на чертежах разнообразные предметы, нужно знать, как в прямоугольных проекциях изображаются вершины (точки), ребра (отрезки прямых линий) и грани предметов (части плоскости).

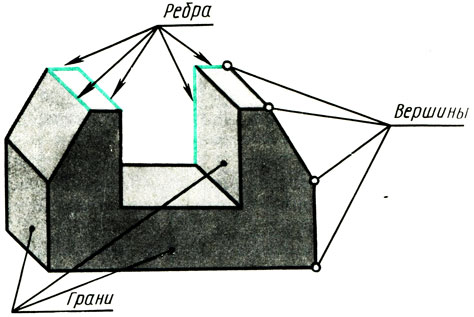
Рис. 108. Предмсч как совокупность точек, пиши. Вершины плоскостей

Проделаем несложный опыт. Проследим, как изображаются в различных положениях плоский предмет и сто элементы.

Примем противоположную окну стену за плоскость проекций. Пусть из окна перпендикулярно стене падают лучи света — проецирующие лучи. Расположим перед стеной (параллельно ей) лист плотной бумаги ABCD (рис. 109, а). На стене образуется тень, равнозначная проекции предмета. Каковы ее размеры? В данном случае проекция a’b’c’d’ по форме и размерам соответствует объекту проецирования — листу

ABCD. Способ проецирования прямоугольный, так как проецирующие лучи перпендикулярны плоскости проекций.

Как будет изменяться проекция, если изображаемый предмет поворачивать, например, вокруг его высоты — ребра AD (рис. 109, б)?

При повороте тень будет сокращаться по ширине (линии а’b’ и c’d’ на рис. 109, б становятся короче). Продолжая поворачивать лист бумаги, заметим, что в положении, перпендикулярном к стене, изображение листа превратится в линию (рис. 109, в), но высота предмета остается постоянной, т. е. линии a’d’ и b’с’ по длине не искажаются.

Теперь сформулируем выводы о том, какие изображения по форме и размерам имеет в прямоугольных проекциях плоский предмет, различно расположенный по отношению к плоскости проекций :

а) плоская фигура, параллельная плоскости проекций, изображается на ней в натуральную величину (рис. 109, а);

б) плоская фигура, наклонная к плоскости проекций, изображается на ней с искажением размеров (рис. 109, б);

в) плоская фигура, перпендикулярная к плоскости проекций, изображается на ней в виде отрезка прямой (рис. 109, в).

Рис. 109. Проецирование плоской фигуры

Эти выводы относятся к изображению граней предметов.

А как в прямоугольных проекциях изображаются ребра предметов, т. е. линии?

Повторим опыт с поворотом плоского предмета, понаблюдаем за тем, как проецируются его ребра, т. е. линии, и сделаем выводы:

а) отрезок прямой, параллельный плоскости проекций, изображается на ней в натуральную величину (сравните высоту предмета AD и ВС на рис. 109, а, б, в с ее проекциями a’d’ и b’с, а ширину предмета АВ и CD с ее проекциями а’b’ и c’d’ на рис. 109, а);

б) отрезок прямой, наклонный к плоскости проекций, изображается на ней с искажением по длине (сравните ширину предмета АВ и CD на рис. 109, б с ее проекциями а’b’ и c’d’);

в) отрезок прямой, перпендикулярный к плоскости проекций, изображается на ней точкой (см. на рис. 109, в ширину предмета — линии АВ и CD, перпендикулярные к плоскости проекций).

Проекцией точки является основание перпендикуляра, опущенного из данной точки в пространстве на плоскость проекций (см. точки а’, b’, с’ , d’ — проекции точек А, В, С, D).

Условимся точки в пространстве обозначать прописными буквами А, В, С, D и т. д., а проекции точек — соответствующими строчными буквами я, Ь, с, d и т. д.

Из двух совпадающих на чертеже точек (рис. 109, в) одна является изображением видимой вершины, а другая — невидимой (закрытой). Обозначение проекций невидимых вершин берут в скобки.

Источник

Прямоугольное проецирование. Урок черчения в 8-м классе

Презентация к уроку

Загрузить презентацию (565 кБ)

Цели урока:

• обучающая: формирование знаний и умений при изучении метода прямоугольного проецирования для выполнении чертежа предмета;
• развивающая: развитие пространственных представлении и пространственного мышления в ходе изучении метода прямоугольного проецирования;
• воспитывающая: воспитание культуры графического труда при выполнении чертежей.

Задачи:

• Обосновать необходимость применения двух и трех плоскостей проекций;
• создать условия для формирования умений проецировать предмет на плоскости проекций;

Тип урока: урок формирования новых знаний.

Методы обучения: объяснение, беседа, упражнения.

Оборудование: конструкция двухгранного и трехгранного угла, чертежные инструменты, плакаты, модели деталей.

Ход урока

I. Организационная часть

II. Актуализация полученных знаний

— Какое существует проецирование?

— Какое проецирование называется центральным?

— Чем центральное проецирование отличается от параллельного?

III. Объяснение новой темы

1. Прямоугольное проецирование на одну плоскость проекций

При прямоугольном проецировании на одну плоскость проекций деталь следует расположить таким образом, чтобы полученное изображение давало наибольшую информацию о ее форме.

Выберем для получения изображения вертикальную плоскость проекции и обозначим ее буквой V. Плоскость, расположенную перед зрителем, называют фронтальной.Перед этой плоскостью расположим деталь. В результате прямоугольного проецирования получим изображение детали, на котором грани предмета, параллельные плоскости проекций, отобразятся в натуральную величину. Полученное изображение называют фронтальной проекцией детали.

Задание. (работа в группе) Установите соответствие главных видов, обозначенных цифрами, деталям, обозначенным буквами, и запишите ответ в тетради.

Задание 1. (самостоятельно) выполните чертеж детали по наглядному изображению макета. Чертеж должен содержать одну проекцию (фронтальную). Нанесите размеры, укажите толщину.

2. Прямоугольное проецирование на две плоскости проекций

Перед учащимися ставится проблемная ситуация.

Задание. (работа в группе) Проанализируйте геометрическую форму детали на фронтальной проекции и найдите эту деталь среди наглядных изображений.

Рис.1. Проанализируйте геометрическую форму детали на фронтальной проекции и найдите эту деталь среди наглядных изображений

Вывод: все 6 деталей имеют одинаковую фронтальную проекцию. Значит, одна проекция не всегда дает полное представление о форме и конструкции детали.

— Какой выход из этой ситуации? (Ответ: Посмотреть на деталь с другой стороны).

Появилась потребность применения ещё одной плоскости проекций.

Вторая плоскость проекций располагается перпендикулярно к фронтальной плоскости.

Эта плоскость в черчении называется горизонтальной плоскостью проекций (плоскость, параллельная земной поверхности) и обозначается латинской буквой H.

— Плоскости V и H пересекаются по оси X, вокруг которой можно вращать плоскость H (показать на модели двугранного угла).

Рис. 2. Проецирования предмета на две плоскости проекций

Итак, помещаем предмет в двугранный угол. Обращаем внимание, что проецирующие лучи перпендикулярны к плоскости проекций. Предмет проецируется на плоскость Н.

Т.к. тетрадный лист плоский в отличие от двугранного угла (или формат листа А4), мы разворачиваем грань угла относительно оси Х на 90 градусов. Совмещаем проецирующие плоскости в одну грань.

Две проекции располагаются в проекционной связи относительно друг друга.

Разберем вопрос с размерами на чертеже.

Рис. 3. Постановка размеров:
на фронтальной проекции проставляется длина и высота;
на горизонтальной проекции – длина и ширина

Метод прямоугольного проецирования на две взаимно перпендикулярные плоскости проекций был разработан французский инженером учёным Гаспаром Монжем в конце 18 века. Метод прямоугольного проецирования называется еще Методом Монжа.

Задание (работа в группе).

Найдите фронтальную и горизонтальную проекции к данному наглядному изображению.

3. Проецирование на три плоскости проекций

Для того чтобы информация о сложной форме детали была представлена достаточно полно, используют проецирование на три взаимно перпендикулярные плоскости проекций: фронтальную, горизонтальную и профильную W (плоскость, расположенная перед зрителем сбоку).
Чтобы построить профильную проекцию предмета, удобно воспользоваться постоянной прямой (линия, которую проводят справа от горизонтальной проекции детали под углом 45 o к оси OX). Линии связи, идущие от горизонтальной проекции, доводят до постоянной прямой. Из точек их пересечения проводят перпендикуляры к горизонтальной прямой и строят профильную проекцию детали. (рассмотреть рис. 91, 92, б учебник)

Система плоскостей проекций представляет собой трехгранный угол с вершиной в точке О. пересечения плоскостей трехгранного угла образуют прямые линии – оси проекций ОХ, ОУ, ОZ.

Помним, что лист тетради (формата) плоский. Для получения чертежа предмета плоскость W поворачивают на 90 o вправо, а плоскость Н — на 90 o вниз. Профильную проекцию располагают в проекционной связи с фронтальной плоскостью, справа от нее на одной высоте.

Чертеж, состоящий из нескольких прямоугольных проекций, называют чертежом в системе прямоугольных проекций.

Задание (работа в группе).

Установите соответствие главных видов, обозначенных цифрами, деталям, обозначенным буквами, и запишите ответ в тетради.

V. Подведение итога урока

Вопросы на закрепление темы урока:

1. С какими плоскостями проекций вы познакомились?

2. Какие размеры проставляются на горизонтальной проекции?

3. Кто обосновал метод прямоугольного проецирования?

4. Как называется комплексный чертеж?

5. В каких случаях применяется прямоугольное проецирование предмета на три плоскости проекций?

4. Закрепление нового материала

Выполнение индивидуальных упражнений по карточкам-заданиям. По наглядному изображению выполнить его фронтальную, горизонтальную и профильную проекции.

5. Итог урока

6. Домашнее задание

• cтр.37-40, пар.16, задание 1.
• стр. 42, задание 2.

Источник

Основы проецирования

Проецированием называется процесс получения изображения предмета на плоскости.

Получившееся при этом изображение называют проекцией. Проекция – в переводе с латинского – «бросать (отбрасывать) вперёд».

В черчении изображения получают по так называемому методу проекций.

Чтобы построить изображение предмета по методу проекций, нужно через точки на предмете провести воображаемые лучи до встречи их с плоскостью. Эти лучи называются проецирующими. Плоскость, на которой получается изображение предмета, называется плоскостью проекций.

Если проецирующие лучи расходятся из одной точки, проецирование называется центральным (рис. 60а). Точка, из которой выходят лучи, называется центром проецирования.

Полученное при этом изображение называется центральной проекцией. Пример: тени, отброшенные от предмета лучами электрической лампочки.

Если проецирующие лучи параллельны друг другу, то проецирование называется параллельным (рис. 60б), а полученное изображение – параллельной проекцией. Пример: солнечные тени.

При параллельном проецировании все лучи падают на плоскость проекций под одним и тем же углом. Если это любой острый угол, то проецирование называется косоугольным (рис. 61а). В косоугольной проекции, как и в центральной, форма и величина предмета искажаются.

Когда проецирующие лучи перпендикулярны к плоскости проекций, проецирование называют прямоугольным (рис. 61б), а полученное изображение – прямоугольной проекцией.

Способ прямоугольного проецирования является основным в черчении.

Проецирование на одну, две и три взаимно перпендикулярные плоскости проекций

Расположим предмет перед плоскостью проекций так, чтобы на получившемся изображении были видны три его стороны (рис. 62).

По такому изображению легко представить пространственный образ предмета.

Такое проецирование в черчении используют для построения наглядных изображений, однако, на наглядных изображениях предметы получают большие искажения и по ним трудно определить истинные размеры предмета.

Теперь расположим предмет перед плоскостью проекций так, чтобы на изображении была видна только одна его сторона, и построим его прямоугольную проекцию (рис. 63а).

На данном изображении проекции рёбер предмета, которые параллельны двум его измерениям (например: длина и ширина), равны натуральным размерам. Но на таком изображении нет третьего измерения предмета (высоты), поэтому оно не наглядно. Такие изображения используют в случаях, когда высота (толщина) детали одинакова во всех её точках (например, чертежи прокладок). Тогда на чертеже такой детали делают запись, указывающую её толщину (высоту). Пример приведен на рис. 63б (S4).

Иногда на одной плоскости изображают предметы, не имеющие одинаковой высоты во всех его точках. Тогда рядом с изображением точки числом указывают её высоту. Такие изображения называют проекциями с числовыми отметками (рис. 63в).

Чтобы судить о трёх измерениях предмета, его необходимо спроецировать ещё на одну плоскость проекций (П₂), которая параллельна другой паре измерений предмета. Тогда вторая плоскость будет расположена перпендикулярно первой плоскости проекций (рис. 64).

Теперь по двум прямоугольным проекциям можно судить о размерах и форме предмета. Хотя форма не всегда ясно выражается двумя проекциями. Поэтому при изображении предметов сложной формы необходимо строить три (а иногда и более) прямоугольных проекции.

Возьмём три взаимно перпендикулярные плоскости проекций (рис. 65).

Одна из них занимает горизонтальное положение, её называют горизонтальной плоскостью проекций и обозначают П₁. Две другие плоскости — вертикальные. Одну называют фронтальной плоскостью проекций (от французского слова «фронталь» – «лицом к зрителю»), другую – профильной плоскостью проекций (от французского слова «профиль» – «вид сбоку») и обозначают соответственно П₂ и П₃.

Линии пересечения плоскостей проекций называют осями проекций и обозначают буквами x, y, z. Точку пересечения осей проекций обозначают буквой О.

В трёхгранный угол, образованный плоскостями проекций, поместим параллелепипед и, проведя проецирующие лучи перпендикулярно плоскостям проекций, получим его проекции. Изображение на плоскости П₁ – горизонтальная проекция, на плоскости П₂ и П₃ – соответственно фронтальная и профильная проекции.

Для получения плоского чертежа трёхгранный угол «разрезают» по оси у, а плоскости П₁ и П 3 поворачивают соответственно вокруг осей х и z по направлению, указанному на рис. 65а стрелками, до совмещения с плоскостью П 2 .

Совмещённые плоскости с построенными на них изображениями предмета показаны на рис. 65б. Линии, соединяющие между собой проекции, называют линиями связи. Линии связи всегда перпендикулярны осям проекций.

На чертежах плоскости проекций не ограничивают и не обозначают. Кроме того, на чертеже при изображении предмета можно не наносить и оси проекций, так как при параллельном проецировании расстояние от плоскости проекций до изображаемого предмета не влияет на очертание его проекций (рис. 66а).

Это даёт возможность устанавливать произвольное расстояние между проекциями, сохраняя между ними проекционную связь даже при отсутствии линий связи (рис. 66б). Такой чертёж называется безосным. При построении проекций здесь пользуются осями симметрии предмета, центровыми линиями или характерными его плоскостями (рис. 67).

Метод прямоугольного проецирования на две и три взаимно перпендикулярные плоскости был разработан французским учёным-геометром Гаспаром Монжем в конце XVIII века. Поэтому его называют ещё методом Монжа.

Г. Монж положил начало развитию новой науки об изображении предметов – начертательной геометрии.

Способы построения третьей проекции

Проекционную связь между горизонтальной и профильной проекциями можно установить несколькими графическими приёмами:

1. дугой окружности (рис. 68а);
2. с помощью прямой под углом 45° (рис. 68б);
3. с помощью постоянной прямой чертежа (рис. 68в).

На рис. 68а,б,в эти приёмы показаны на примере построения третьей проекции точки.

Удобнее всего пользоваться третьим способом, т.к. при наименьшем количестве графических операций достигается большая точность построения.

Если три вида уже построены, то место постоянной прямой чертежа произвольно выбирать нельзя. Нужно найти точку, через которую она пройдет. Для этого достаточно продолжить до взаимного пересечения горизонтальную и профильную проекции оси симметрии предмета. Через полученную точку К под углом 45° проводят отрезок прямой. Если осей симметрии на чертеже нет, то продолжают до пересечения в точке К₁ горизонтальную и профильную проекции любой грани, проецирующейся в виде отрезков прямой (рис. 69).

Источник