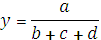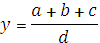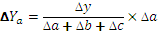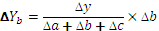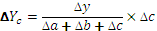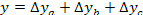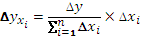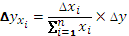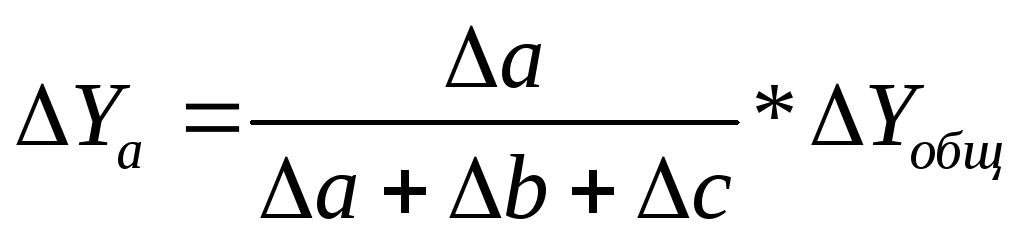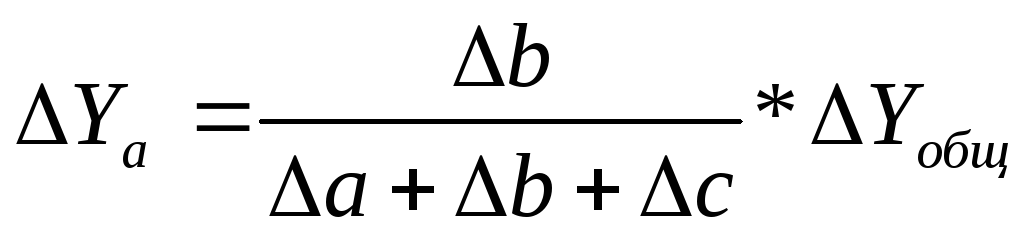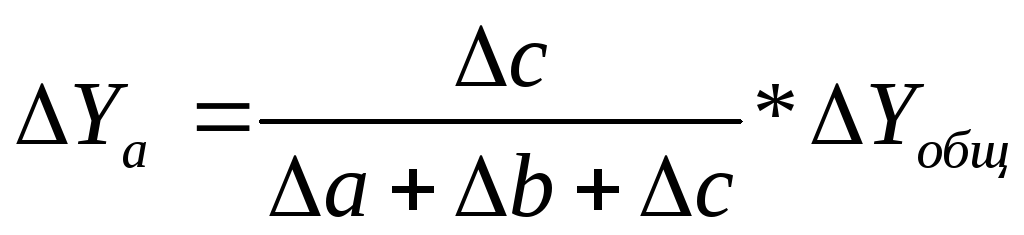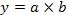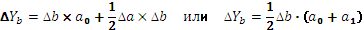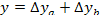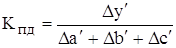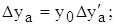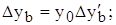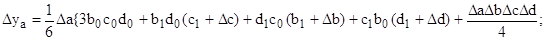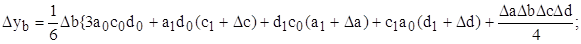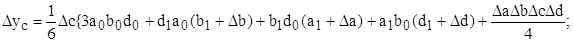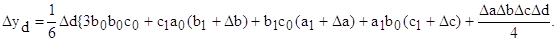6.2 Способы пропорционального деления и долевого участия
Способ пропорционального деления. Данный способ применяется для определения величины влияния факторов на изменение результативного показателя в аддитивных и смешанных моделях кратно-аддитивного типа:
Суть способа пропорционального деления состоит в том, что необходимо общее изменение результативного показателя распределить пропорционально влиянию каждого фактора.
Алгоритм расчета влияния факторов на изменение результативного показателя в аддитивных моделях включает следующие этапы:
1 этап. Построение факторной модели результативного показателя:
где у — результативный показатель;
а, b, с — факторные показатели, имеющие с результативным показателем аддитивную зависимость.
2 этап. Определение абсолютного изменения результативного показателя:
3 этап. Расчет влияния факторов на изменение результативного показателя:
4 этап. Проведение балансовой увязки полученных результатов:
∆
5 этап. Формулирование выводов по результатам проведенного анализа.
Таким образом, рассчитать влияние факторов в аддитивной факторной модели способом пропорционального деления можно следующим образом:
где ∆уXi— абсолютное изменение результативного показателя под влиянием хi-го фактора;
∆у — абсолютное изменение результативного показателя;
∆хi — абсолютное отклонение хi-го фактора, влияющего на изменение результативного показателя;
п — количество факторов, влияющих на изменение результативного показателя.
Способ долевого участия. Данный способ применяется для расчета влияния факторов в аддитивных и смешанных моделях кратно-аддитивного типа.
Суть способа долевого участия состоит в том, что необходимо определить долю влияния каждого фактора в общем изменении результативного показателя, которая затем умножается на общий прирост результативного показателя.
В аддитивной модели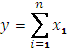 
расчет влияния факторов производится следующим образом:
Алгоритм расчета влияния факторов будет выглядеть следующим образом:
6.3 Интегральный способ в анализе хозяйственной деятельности
Элиминирование как способ детерминированного факторного анализа имеет существенный недостаток, так как при его использовании исходят из того, что факторы изменяются независимо друг от друга. На самом же деле они изменяются совместно, взаимосвязанно, и от этого взаимодействия получается дополнительный прирост результативного показателя, который при использовании приема элиминирования присоединяется к одному из факторов, как правило, последнему. В связи с этим величина влияния факторов на изменение результативного показателя меняется в зависимости от месторасположения фактора в детерминированной факторной модели. Для устранения указанного недостатка используются интегральный способ и способ логарифмирования.
Интегральный способ применяется для измерения влияния факторов на изменение результативного показателя в мультипликативных, кратных и смешанных кратно-аддитивных моделях.
Использование данного способа позволяет получать более точные результаты расчета влияния факторов по сравнению со способами элиминирования, так как дополнительный прирост результативного показателя от взаимодействия факторов присоединяется не к последнему фактору, а делится поровну между ними.
Алгоритм расчета влияния факторов на изменение результативного показателя в двухфакторной мультипликативной модели интегральным способом включает следующие этапы.
1 этап. Построение факторной модели результативного показателя:
где у — результативный показатель;
а, b — факторные показатели, имеющие с результативным показателем мультипликативную зависимость.
2 этап. Определение абсолютного изменения результативного показателя:
3 этап. Расчет влияния факторов на абсолютное изменение результативного показателя:
4 этап. Проведение балансовой увязки полученных результатов:
∆
5 этап. Формулирование выводов по результатам проведенного анализа.
Для расчета влияния факторов на изменение результативного показателя в других типах детерминированных факторных моделей используются следующие рабочие формулы, приведенные в таблице 6.1.
Таким образом, использование интегрального способа не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы подставить необходимые числовые данные и произвести расчеты с помощью калькулятора или ПЭВМ в Ехсе1.
Таблица 6.1 – Алгоритм расчета влияния факторов интегральным способом
Источник
Способ пропорционального деления или долевого участия
5. Способ пропорционального деления или долевого участия
Сущность способа пропорционального деления состоит в пропорциональном делении прироста результативного показателя по факторам его обусловившим, а долевого участия — в определении доли участия каждого фактора в общем приросте результативного показателя.
Эти способы применяются для аддитивных, мультипликативных, кратных и смешанных моделей типа 
.
Для определения влияния отдельных факторов на прирост результативного показателя рассчитывается один из следующих коэффициентов:
1) коэффициент пропорционального деления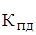 
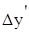
, как отношение общего относительного прироста результативного показателя 
к сумме относительных изменений факторных показателей.
При аддитивных типах моделей рассчитывается один коэффициент пропорциональности, а при других типах моделей — он определяется для каждого порядка факторов в отдельности.
При исходной модели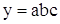 
, 
(изменения всех составляющих взяты в относительных единицах).
;
; 
;
.
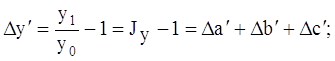
2) коэффициент долевого участия 
, который определяется как отношение относительного прироста i‑го факторного показателя к сумме относительных изменений факторных показателей.
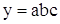
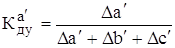
Например, для исходной факторной модели , коэффициент долевого участия для фактора «а»:
.
Тогда для приведенной исходной мультипликативной модели:
;
;
;
.
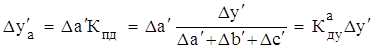
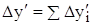
Переход от относительных единиц к абсолютным осуществляется по формулам:
; 
.
Если взаимосвязь факторов двух уровневая (n-уровневая), то необходимо рассчитывать коэффициент пропорционального деления для каждого уровня, а коэффициент долевого участия для каждого факторного показателя соответствующего уровня.
6. Интегральный способ
Для приемов элиминирования характерны следующие недостатки:
величина влияния фактора на изменение результативного показателя зависит от места расположения фактора в детерминированной модели;
дополнительный прирост результативного показателя, полученный от совместного взаимодействия факторов, присоединяется к последнему фактору.
Интегральный метод не имеет этих недостатков. Величина влияния фактора на изменение результативного показателя не зависит от места расположения фактора в детерминированной модели. Дополнительный прирост от совместного взаимодействия факторов, распределяется между ними поровну.
Метод применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях типа 
.
Для мультипликативных моделей:
Исходная модель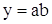 
.
; 
.
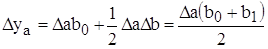
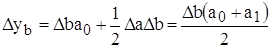
Исходная модель
; 
;
.
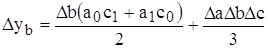
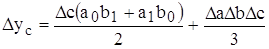
Исходная модель 
Кратная модель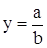 
; 
; 
.
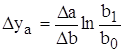
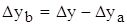
Смешанная модель типа: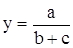 
; 
;
;
;
;
;
;
.
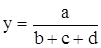
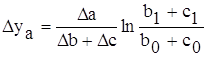
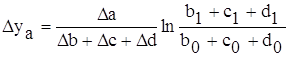
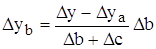
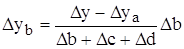
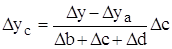
7. Способ логарифмирования
Применяется для измерения влияния факторов в мультипликативных моделях.
Результат расчета влияния факторов на результативный показатель при этом способе не зависит от места расположения факторов в модели. Дополнительный прирост от совместного взаимодействия факторов распределяется между ними пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя.
Исходная модель
; 
; 
.
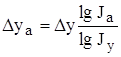
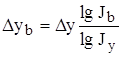
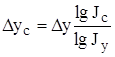
1. Экономика предприятия (фирмы): Учебник / Под. ред. проф. О.И.Волкова. – М.: ИНФРА-М, 2005. – 601 с.
2. Грузинов В.П., Грибов В.Д. Экономика предприятия: Учеб. пособие – М.: Финансы и статистика, 2005. – 208 с.
3. Сергеев И.В. Экономика предприятия. Учеб. пособие. – М.: Финансы и статистика, 2005. – 304 с.
4. Экономика предприятия / Под ред. Е.Л.Кантора. – СПб.: Питер, 2006. – 352 с.
Источник
