Способ проецирования аксонометрических проекций

Черчение. 10 класс

§ 17. Основные положения аксонометрического проецирования

Основные положения аксонометрического проецирования

Проецирование предмета на плоскости проекций дает нам представление о форме самого предмета только с одной стороны. Чтобы получить представление о форме предмета в целом, нужно проанализировать и сравнить между собой отдельные его проекции. Предмет можно спроецировать на плоскость проекций таким образом, чтобы на созданном изображении было видно сразу несколько его сторон. Полученное таким образом изображение называется наглядным. Его используют для реализации технического замысла автора при выполнении проектирования и конструирования разных объектов (рис. 53).
Для получения наглядного изображения предмета используют аксонометрическую проекцию (рис. 54).

Аксонометрическая проекция — это изображение, полученное при параллельном проецировании предмета вместе с осями прямоугольных координат на произвольную плоскость.

Слово аксонометрия — греческое. В переводе оно означает «измерение по осям» (аксон — ось, метрео — измеряю).

Проецируемый предмет располагают относительно координатных осей х, у, z и вместе с ними проецируют его на произвольную плоскость. Эта плоскость называется плоскостью аксонометрических проекций. Проекции координатных осей называются аксонометрическими осями (см. рис. 54).

Виды аксонометрических проекций.

Аксонометрическое изображение предмета получается прямоугольным (а) и косоугольным (б) проецированием.
Проецирующие лучи в прямоугольной аксонометрической проекции перпендикулярны плоскости проекции. К прямоугольным аксонометрическим проекциям относятся изометрическая и диметрическая проекции.
Проецирующие лучи в косоугольной аксонометрической проекции направлены под углом к плоскости проекций. К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции.

Какой вид аксонометрической проекции (прямоугольную или косоугольную) вы будете использовать для наглядного изображения объекта? Свой выбор объясните.

Коэффициент искажения. Все виды аксонометрических проекций характеризуются двумя параметрами: направлением аксонометрических осей и коэффициентами искажения по этим осям.

Коэффициент искажения (k) — отношение аксонометрической единицы измерения к натуральной.

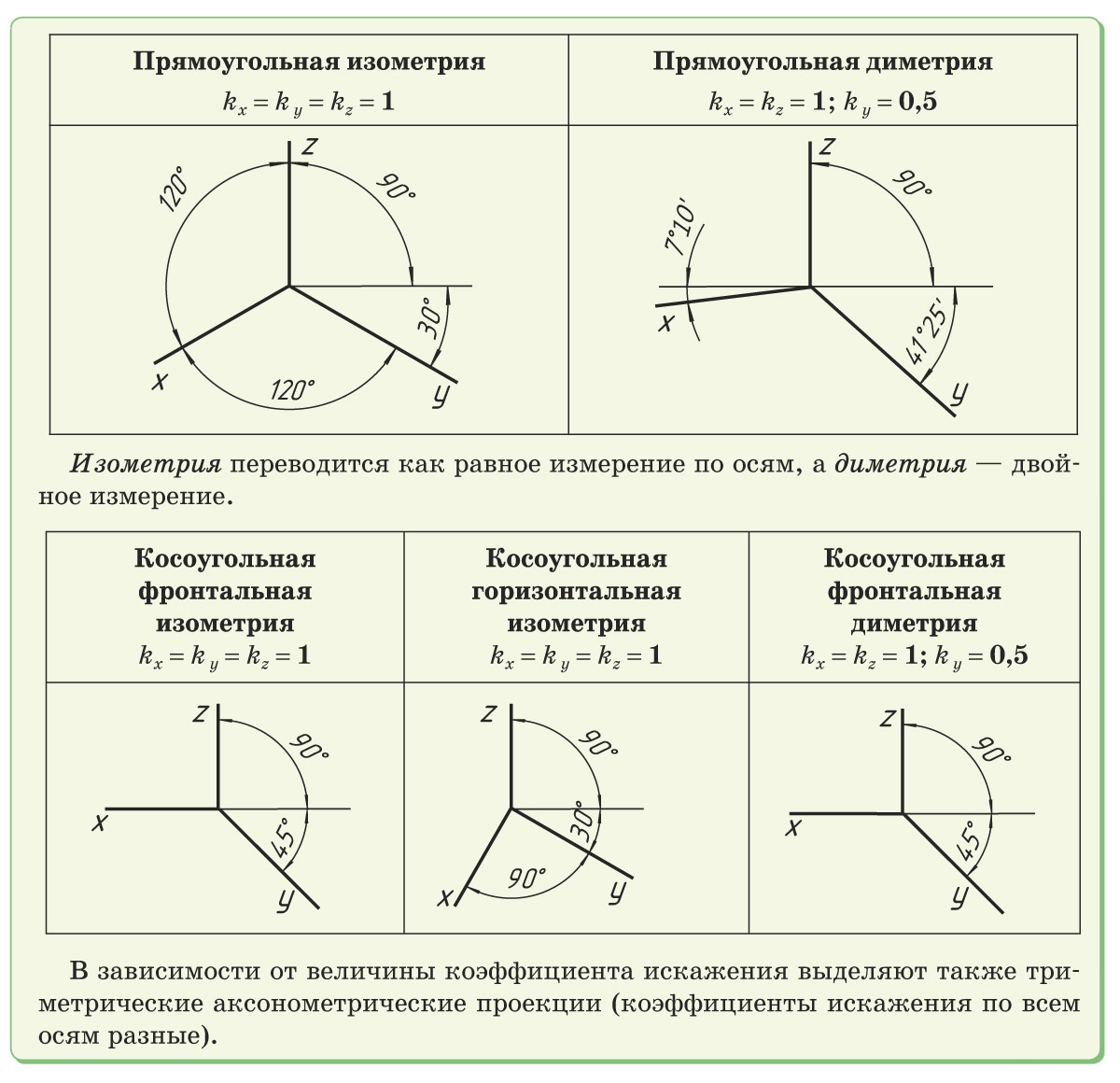
В зависимости от расположения координатных аксонометрических осей относительно аксонометрических проекций получаются различные аксонометрические проекции: прямоугольная изометрическая проекция (сокращенно — изометрия), прямоугольная диметрическая проекция (или диметрия), косоугольные фронтальная и горизонтальная изометрия и фронтальная диметрия.
Например, в прямоугольной изометрической проекции оксонометрические оси располагаются по отношению друг к другу под углом 120°.
Коэффициенты искажения различны в изометрических и диметрических аксонометрических проекциях. В изометрической проекции коэффициент (k) равен единице, т. е. по осям х, y, z выполняют проекцию без искажения. Диметрическая проекция выполняется с коэффициентом искажения (k) по оси y, равным 0,5, а по осям z и х — равным единице.

Объясните, в чем отличие изометрической проекции от диметрической.

Наиболее распространенными являются прямоугольная изометрическая (прямоугольная изометрия) и косоугольная фронтальная диметрическая (фронтальная диметрия) проекции, в которых объект изображается в трех проекциях так, чтобы можно было хорошо увидеть его форму с трех сторон.
Способы построения аксонометрических осей. При построении аксонометрических осей прямоугольной изометрии используют один из трех способов.

Правила построения аксонометрических проекций
1. Длина откладывается по оси х, высота — по оси z, ширина — по оси у.
2. Все измерения выполняются только по аксонометрическим осям или прямым, параллельным им.
3. Все прямые линии, параллельные друг другу или осям x, y, z, на комплексном чертеже в аксонометрических проекциях остаются параллельными между собой и соответствующим аксонометрическим осям

В начале 80-х гг. XX в. в компьютерных играх стала активно применяться изометрическая проекция. Это быстрая и эффективная симуляция трехмерного пространства, которая дает иллюзию глубины без большого количества дорогостоящих вычислений. Раньше большинство игр имели вид сверху или вид сбоку. Первыми играми, которые использовали изометрию, были Zaxxon и Qbert. Сейчас, несмотря на развитие 3D-технологий, игры с изометрическим видом все еще очень популярны, особенно ролевые и стратегии.

Источник

Аксонометрические проекции

Во многих случаях при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения. Для построения таких изображений применяются проекции, называемые аксонометрическими .

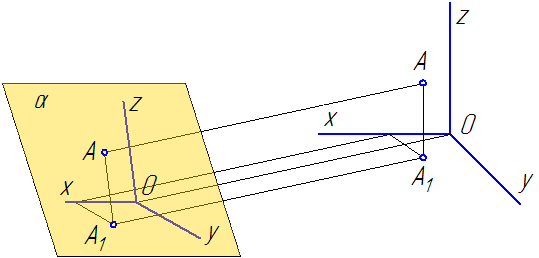
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).

Рисунок 4.1
Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
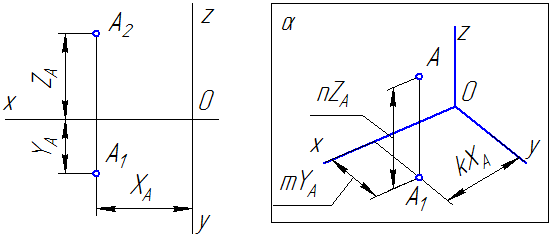
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.

Рисунок 4.2
Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:

• прямоугольные изометрические и диметрические;
• косоугольные фронтально изометрические, горизонтально изометрические и фронтально диметрические;

Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.

4.1. Прямоугольные проекции

4.1.1. Изометрическая проекция

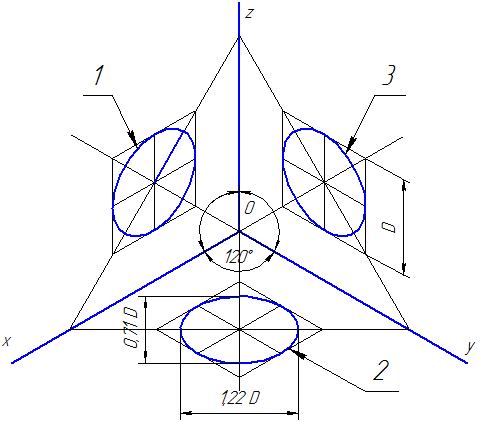
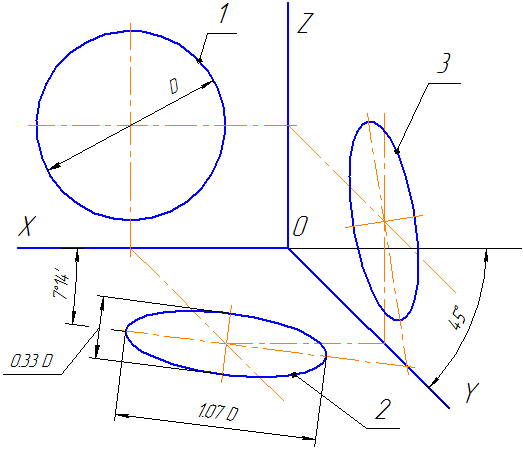
Направление аксонометрических осей приведено на Рисунке 4.3.

Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции

Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.

Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

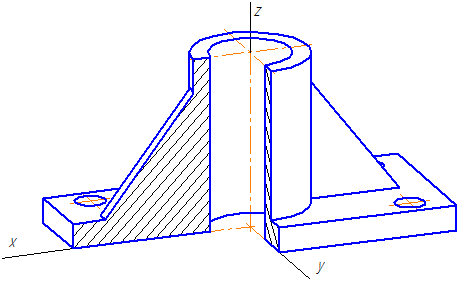
Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.

Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции

4.1.2. Диметрическая проекция

Положение аксонометрических осей проводится на Рисунке 4.5.

Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.

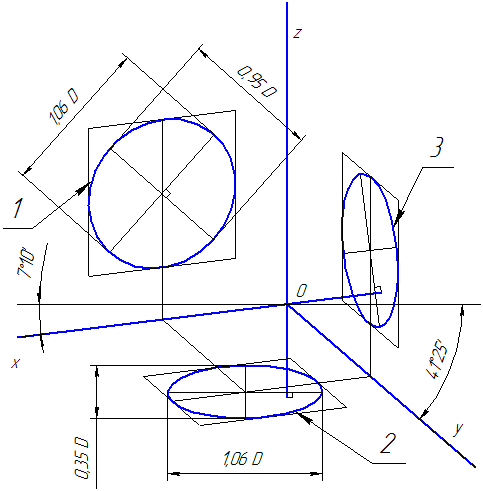
Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

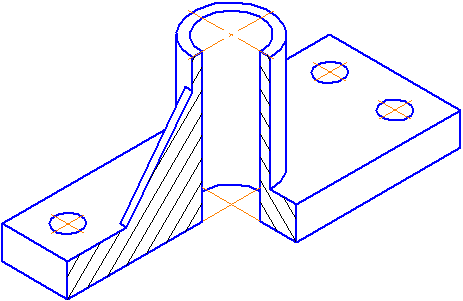
Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.

Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции

Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции

4.2 Косоугольные проекции

4.2.1 Фронтальная диметрическая проекция

Положение аксонометрических осей приведено на Рисунке 4.7. Допускается применять фронтальные диметрические проекции с углом наклона к оси OY, равным 30 0 и 60 0 .

Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.

Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.

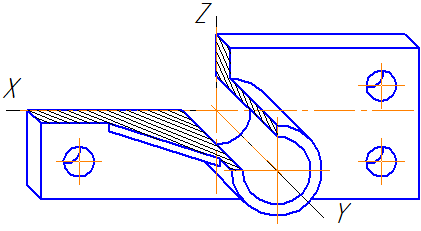
Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.

Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.

Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции

4.3 Построение эллипса

4.3.1 Построения эллипса по двум осям

На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).

Одна из этих окружностей делится на несколько равных (или неравных) частей.

Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.

Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.

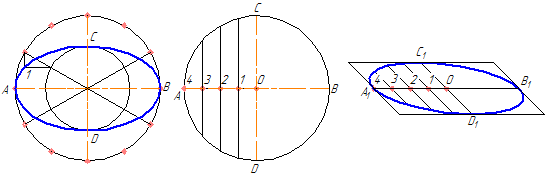
а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)

4.3.2 Построение эллипса по хордам

Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А₁В₁=АВ и С₁ D₁ = 0,5CD. Диаметр А ₁В₁ делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).

4.4 Штриховка сечений

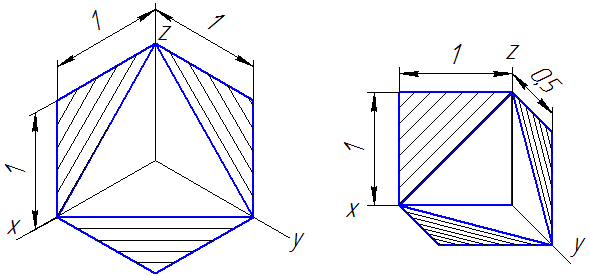
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).

а б
Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях

Источник