Способ проекции карты мира

На выбор проекции для конкретной карты влияет ряд факторов, в первую очередь назначение карты (требования потребителей) и пространственные особенности территории.

Прежде всего, исходя из назначения карты, устанавливают предпочтительный характер искажений. Карты, используемые для измерения азимутов и углов, целесообразно строить в равноугольных проекциях. Например, для морских навигационных карт применяют цилиндрическую проекцию Меркатора, в которой линия, пересекающая меридианы на эллипсоиде под одним и тем же углом (так называемая локсодромия), изображается прямой: судно, которое держит определенный курс (азимут), движется по локсодромии. Опыт показывает, что равноугольные проекции удовлетворяют запросы многих потребителей. Однако при необходимости производить по картам измерения или сравнение площадей (что, например, существенно для некоторых экономических карт) обращаются к проекциям равновеликим. Когда чрезмерные искажения углов и площадей одинаково нежелательны (например, на картах полушарий), берут одну из произвольных проекций.

Учет пространственных факторов, т. е. размеров, формы и положения картографируемой территории, позволяет найти в избранной группе проекций (равноугольных, равновеликих, произвольных) проекцию, обладающую наименьшими искажениями или их выгодным распределением, или другими ценными для карты свойствами.

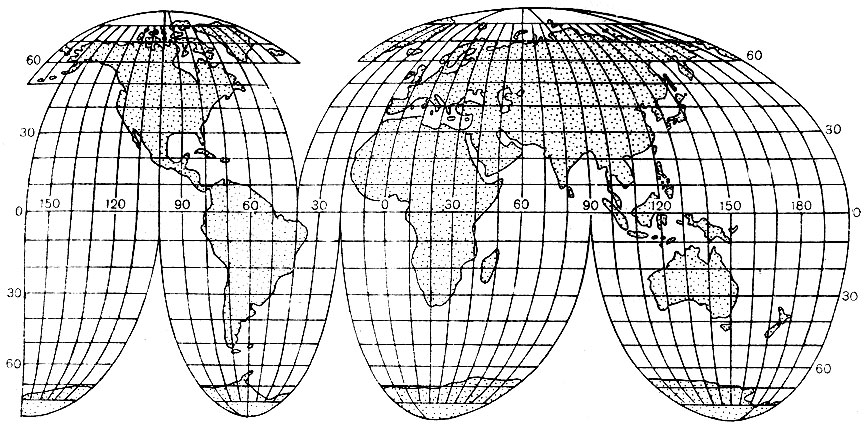
Для карт мира широко использовались цилиндрические и псевдоцилиндрические проекции, имеющие сетки с прямолинейными и параллельными друг другу параллелями, что ценно при изучении явлений широтной зональности. В цилиндрических проекциях изображения повторяющихся территорий (см. рис. 2.28) одинаковы. Чтобы уменьшить искажения в высоких широтах, можно строить проекцию на секущем Цилиндре.

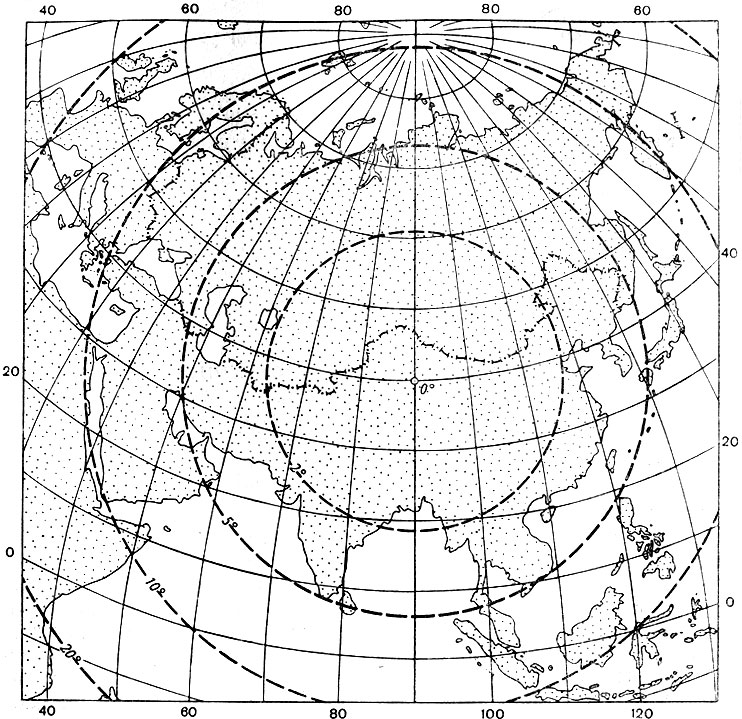
Рис. 2.16. Картографическая сетка в косой равновеликой азимутальной проекции (Ламберта) с изоколами углов

Например, на многих картах Большого советского атласа мира (БСАМ) (см. § 8.8) была использована цилиндрическая проекция, сохраняющая главные масштабы по параллели 30 ° Псевдоцилиндрические проекции (рис. 2.8) по сравнению с цилиндрическими дают в высоких широтах меньшие искажения площадей, но увеличивают искажения углов, что сказывается особенно неблагоприятно на изображениях повторяющихся территорий, например Северной и Южной Америки.

Теперь более употребительны поликонические проекции с малой кривизной параллелей, слабо возрастающей к полюсам, обладающие меньшими и уравновешенными искажениями углов и площадей Кривизна их меридианов и параллелей как бы отражает эллипсоидальность планеты.

Карты полушарий естественно строить в азимутальных проекциях. Ранее широко применялись равноугольная стереографическая проекция (см. рис. 2.14) и равновеликая Ламберта (см. рис. 2.15). Первой из них на краях полушария свойственны большие искажения площадей (р=4), второй — искажения углов (со=39 ° ). Поэтому в настоящее время для учебных карт предлагают произвольные азимутальные проекции, промежуточные по величине искажения ( В экваториальной азимутальной проекции, предложенной Г. А. Гинзбургом, на краях полушария р= 1,22, ω = 29 ° 6.).

Для карт отдельных материков (Европы, Азии, Северной Америки, Южной Америки, Австралии с Океанией) применяют преимущественно равновеликую косую азимутальную проекцию Ламберта с точкой нулевых искажений в центре изображаемого материка.

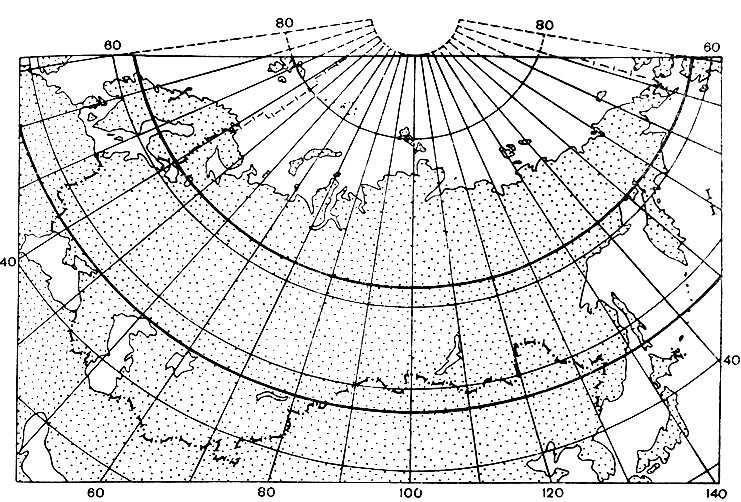
Рис. 2.17. Картографическая сетка для карт СССР в равнопромежуточной конической проекции В. В. Каврайского; параллели сечения 47 и 62sup°/sup с. ш. утолщены

Для Африки косая проекция заменяется экваториальной. В азимутальной проекции искажения нарастают по мере удаления от центра проекции и потому достигают наибольшей величины в углах прямоугольной рамки карты. Так, на карте Азии в пределах материка угловые искажения достигают 15 ° (рис. 2.16).

Карты СССР, изображающие страну в целом, составляются главным образом в нормальных конических проекциях, равнопромежу-точных по меридианам; разработанные В. В. Каврайским (рис. 2.17) и Ф. Н. Красовским, они не имеют принципиальных различий, но проекция Красовского дает несколько меньшие искажения для крайних северных районов СССР.

Нормальные конические проекции в применении для карт СССР не позволяют показать точку полюса и вследствие значительной кривизны параллелей как бы поднимают восточные и западные части СССР, что нарушает зрительное представление о широтных зонах. Эти недочеты, нежелательные для учебных карт, могут быть устранены при использовании других проекций, имеющих, однако, большие искажения по сравнению с коническими.

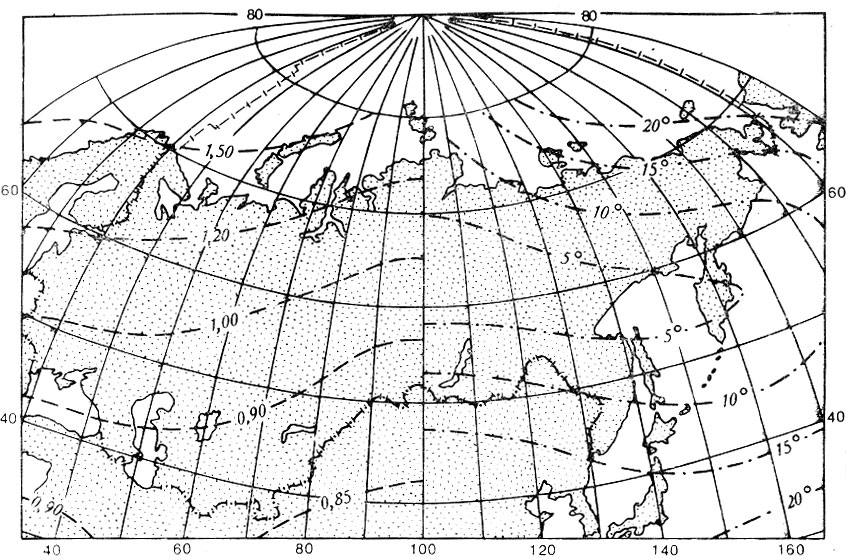
В частности, на картах СССР для начальной школы теперь используется произвольная проекция, симметричная относительно центрального меридиана 100 ° в. д. В ней Северный полюс лежит в рамке карты, кривизна параллелей мала, но возрастают искажения углов и площадей. В частности, искажения площадей достигают на северо-востоке и северо-западе материковой части СССР 20-40% (рис 2 18) а искажения углов увеличиваются до 15-20 ° .

Рис. 2.18. Картографическая сетка для карт СССР в произвольной проекции ЦНИИГАиК с изоколами площадей (на левой половине рисунка) и углов (справа)

В выборе проекций большую роль играет математический момент — величина искажений. Но этот признак не всегда решающий. Ярким примером этому служит использование для морских навигационных карт нормальной равноугольной цилиндрической проекции Меркатора (см. рис. 2.13). При сохранении главного масштаба на экваторе площади преувеличиваются на параллели 60 ° в 4 раза, а на параллели 80 ° — более чем в 30 раз. Но в этой проекции курсы корабля (локсодромии) изображаются прямыми линиями, а учет искажений длин, необходимый при определении пройденных расстояний, не вызывает затруднений.

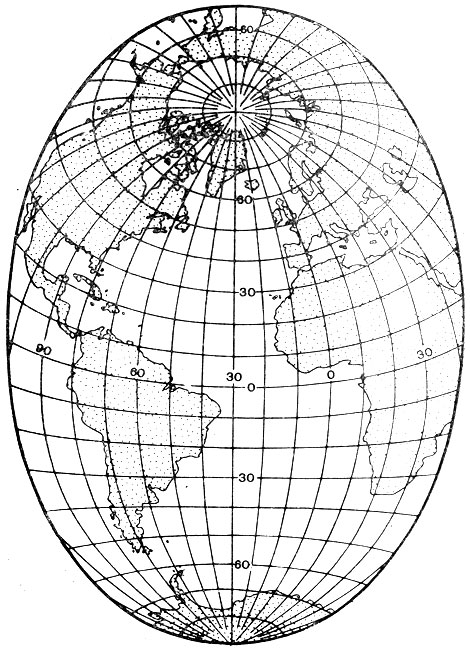
В других случаях важно учитывать географические требования в отношении целостного изображения взаимосвязанных объектов (например, Атлантического океана совместно с Северным Ледовитым, рис. 2.19), наилучшего показа основных для темы карты пространств и т. п.

По мере уменьшения масштаба значение географических требований к выбору проекций возрастает. Напротив, для крупного и среднего масштабов на первый план выступает математический фактор; карты этих масштабов часто используются в инженерных и оборонных целях, вследствие чего измерения по ним должны отличаться простотой и давать результаты большой точности. Это возможно при практически неощутимых искажениях. Однако при изображении обширных территорий любая проекция дает крупные искажения. Выход был найден в первой половине XIX в., когда стали применять так называемые «многогранные проекции».

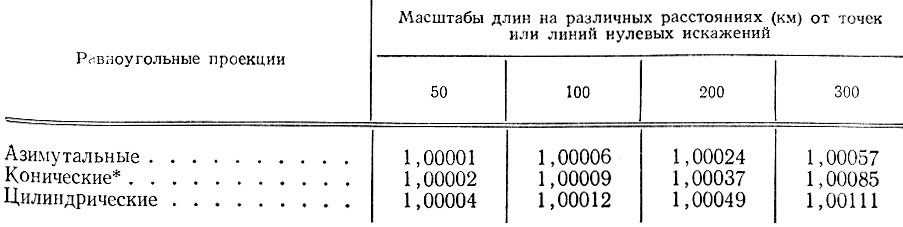
Как было сказано ранее, искажения возрастают по мере удаления от точек или линий, сохраняющих главный масштаб. В равноугольных проекциях искажения длин увеличиваются пропорционально квадрату этого удаления. В табл. 2.1 приводятся масштабы длин для расстояний 50, 100, 200 и 300 км от названных точек или линий равноугольных проекций. Из этого можно сделать вывод, что при картографировании ограниченного пространства практически можно не учитывать искажений длин и считать в этом смысле различные равноугольные проекции равноценными. Это значит, что при создании карт на большую территорию можно ограничить искажения пренебрегаемыми величинами, если изображать ее по частям. Для этого есть разные пути. Первоначально прибегали к замене земного эллипсоида многогранником, вписанным в эллипсоид (или описанным около него). Отдельные грани соответствуют трапециям эллипсоида, изображаемым на отдельных листах карты данного масштаба.

Рис. 2.19. Совместное изображение Атлантического и Северного Ледовитого океанов

При крупных масштабах, когда один лист карты покрывает незначительную территорию, каждую грань многогранника можно считать совпадающей с поверхностью эллипсоида, т. е. принять поверхность эллипсоида плоской в пределах каждой грани.

Таблица 2.1. Масштабы длин в равноугольных проекциях

( Масштабы длин в конической проекции зависят от широты параллели с нулевыми искажениями.)

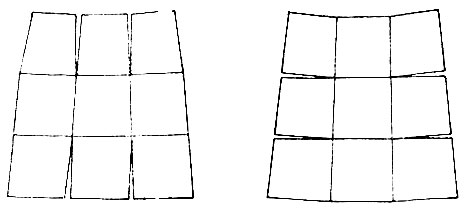
В этом случае изображение практически свободно от искажения; но если развернуть поверхность многогранника на плоскость (рис. 2.20), то между отдельными гранями (листами карты) образуются разрывы.

Рис. 2.20. Разрывы при соединении по рамкам листов карты, построенной в многогранной проекции

Листы карт не могут быть сведены в одно целое.

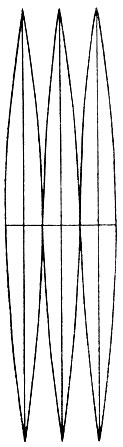
Рис. 2.21. Многополосное построение — изображение двуугольников земного эллипсоида в поперечной цилиндрической равноугольной проекции Гаусса

Искажения исключаются за счет потери непрерывности изображения. Просветы увеличиваются постепенно; при соединении четырех и даже девяти листов крупномасштабной карты ими можно практически пренебречь, но при большом количестве листов работа с картой затруднена.

Поэтому после первой мировой войны во многих странах стали постепенно вводить для топографических карт равноугольную поперечно — цилиндрическую проекцию, хорошо изображающую части земной поверхности, вытянутые вдоль меридианов. При ее применении поверхность эллипсоида разделяется меридианами на зоны, каждая из которых изображается на плоскости самостоятельно (рис. 2.21). Таким образом, «многогранная проекция» заменена «многополосной». В СССР эту проекцию называют проекцией Гаусса, а за рубежом, когда ее вычисляют несколько другим путем, она известна как поперечная проекция Меркатора (на осевом меридиане зон μ=1, международное обозначение проекции ТМ) или универсальная проекция Меркатора (μ=0,99960, обозначение проекции ИТМ).

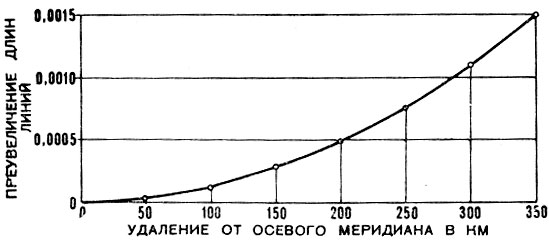
Рис. 2.22. Увеличение искажений длин в проекции Гаусса на разных расстояниях от среднего меридиана

Для топографических и обзорно-топографических карт масштабов 1 : 10 000-1 : 1 000 000 зоны, ограниченные меридианами, отстоящими друг от друга на 6 ° , совпадают с колоннами листов миллионной карты. Искажения (преувеличение) длин линий на краях плоского изображения таких зон в проекции Гаусса составляют 0,000 9, 0,000 6, 0,000 4 и 0,000 3 соответственно на параллелях 40, 50, 60 и 70 ° , что позволяет не считаться с ними при практическом использовании топографических карт. Увеличение искажений по мере удаления от среднего меридиана показано на рис. 2.22. Для масштабов 1:2000-1:5000 ширина зон установлена в 3 ° .

Многополосная проекция создает разрывы по краям зон, но позволяет соединить в одно целое листы внутри всей зоны и считать в пределах зоны масштаб практически постоянным.

Рис. 2.23. Картографическая сетка для карты мира в псевдоцилиндрической проекции с разрывами по океанам

Разрывы изображения могут использоваться также при построении проекций мировых карт, когда нет необходимости в целостном изображении океанов (например, на почвенной карте мира) или материков. В первом случае (рис. 2.23) каждый материк строится по своему среднему меридиану, что значительно улучшает изображение материков за счет разрезов (потери непрерывности изображения) на океанах.

Источник

Картографические проекции. Урок 6

Картографические проекции сегодня – это математические способы изображения всего земного эллипсоида или его части на плоскости, систематическое преобразование широт и долгот с поверхности сферы на плоскость.

Для создания географических карт выполняют две последовательных операции:

Перенесение (проектирование) поверхности геоида с его сложным рельефом на поверхность эллипсоида вращения или шара.
Дальнейшее его проектирование на плоскость (преобразование системы географических координат в декартовы) с использованием одной из картографических проекций.

При этом картографы пытаются добиться как можно меньшего количества искажений. Сделать мелкомасштабную карту совсем без искажений невозможно. На крупномасштабных (топографических) картах искажения почти отсутствуют. В зависимости от назначения карты одни погрешности допустимы, другие нет. Поэтому и существуют разные типы проекций, предназначенные для сохранения некоторых свойств сферы за счёт других её свойств.

Проекция на шар — глобус. Автор: UBC Library Digitization Centre

Виды искажений при использовании картографических проекций

Разложить на плоскости эллипс или шар очень трудно, для того, чтобы убедиться в этом, можно попробовать это сделать на практике. Сложить кусочки апельсиновой кожуры так, чтобы между ними не было пустых мест и попробовать получить непрерывную ровную плоскость. Корка соберётся в складки, она не уложится без промежутков.

При любом способе разложения шара на плоскость присутствует один или несколько типов искажения:

базовое – искажение расстояний (длин линий), от него зависит степень других видов деформаций. Признак: между соседними параллелями отрезки меридианов неодинаковы по длине;
площадей. При таком искажении между соседними параллелями форма и величина (а значит и площадь) ячеек неодинакова;
углов – углы между определённым направлением на местности и на карте не совпадают. Узнать его можно по тому, что углы между параллелями и меридианами не являются прямыми;
форм. При одинаковой площади форма клеток, находящихся на одной широте, разная.

При этом типы искажений взаимозависимы, при уменьшении одного из показателей увеличивается другой. В зависимости от назначения карты, на ней присутствуют места с нулевым искажением, с удалением от него количество искажений увеличивается. Поэтому на карте есть три вида масштаба:

основной (тот, что подписан), действующий на линии нулевого искажения,
частные (определяются при помощи эллипса искажений), их может быть бесконечно много;
средний (совокупность частных масштабов отрезка).

При выборе типа картографической проекции сначала строят изоколы – изолинии, соединяющие точки с одинаковым искажением.

Изоколы искажения углов
Источник: https://ds04.infourok.ru/uploads/ex/0617/00148bfe-04623ef1/hello_html_329bd6b7.jpg

Типы проекций по характеру искажений

Для разных целей нужны карты с отсутствием тех или иных видов искажений. При помощи разных проекций можно сделать так чтобы на них отсутствовали погрешности либо углов, либо длин, либо площадей. Чем больше искажаются углы, тем меньше искажаются площади и наоборот. По характеру искажений все картографические проекции делят на:

равноугольные (конформные);
равновеликие (эквивалентные);
произвольные:
- равнопромежуточные (эквидистантные).

Равноугольные картографические проекции

На картах, построенных по этому типу, нет искажений направлений и углов. Направления на местности совпадают с таковыми на карте, прямые линии на местности остаются прямыми на карте. Они используются для прокладки точных маршрутов и применяется на навигационных и топографических картах.

Зато на них сильно изменены площади объектов Земли и линейный масштаб карты зависит от положения на ней данной точки. Типичный пример равноугольной проекции – цилиндрическая проекция Герхарда Меркатора (Герарда Кремера), созданная ещё в 1569 г и используемая в морской навигации до сих пор. Примером использования Проекции Меркатора является равноугольная проекция Гаусса-Крюгера.

В этой проекции создаются отдельные океанологические, климатические и геофизические карты.

Проекция Меркатора.
Файл доступен по лицензии: Creative Commons Attribution-Share Alike 3.0 Unported

Равновеликие картографические проекции

Это проекции для построении карт, на которых нет искажения площадей (масштаб площадей имеет везде одну и ту же величину), зато сильно растёт погрешность форм и углов (материки и океаны в высоких широтах сплющиваются). Картами, построенными в равновеликих проекциях, удобно пользоваться для расчета площадей, например типов почв, посадок кукурузы, облесенности материков, загрязнения океана или радиоактивного загрязнения суши и др.

Их применяют для составления климатических, почвенных, геофизических, геологических, зоогеографических, геоботанических, экономических, исторических, этнографических, административных карт.

Пример равновеликой проекции. Автор: CC BY-SA 3.0

Произвольные картографические проекции

Углы и площади здесь искажаются, но значительно меньше, чем в предыдущих двух проекциях. Поэтому они наиболее используемы. Произвольные картографические проекции не относятся ни к равновеликим, ни к равноугольным.

Произвольная проекция Робинсона. Автор: CC BY-SA 3.0

Равнопромежуточные картографические проекции

Это тип произвольных картографических проекций. В них масштаб длин одного из главных направлений остаётся неизменным. Пример: прямая азимутальная проекция. Равнопромежуточные проекции используют для создания общегеографических, физических, тектонических, политических и др. видов карт.

Характер искажения всегда входит в общее название проекции (равновеликая азимутальная, равноугольная коническая, равновеликая цилиндрическая и т.д.).

Интересно,

что д ревнейшей картографической проекцией является гномическая проекция, применённая на картах звёздного неба Фалесом Милетским ещё в Древней Греции.

Равнопромежуточная коническая проекция. Автор: CC BY-SA 3.0

Классификация географических проекций по геометрической фигуре, являющейся вспомогательной поверхностью

На плоскость эллипсоид проектируют при помощи геометрических фигур, а поверхности, на которые он проектируется, могут быть секущими (разрезающей) фигуру или касательными (соприкасается, но не разрезает глобус) к ней. При этом на полученной карте касательные и секущие линии (стандартные) представлены неискажёнными.

Проекции также бывают по-разному ориентированы.

Нормальными называют проекции, в которых оси вспомогательной поверхности совмещаются с осью земного эллипсоида или шара, а спроектированная поверхность размещается касательно к полюсу.
Поперечными – ось располагают под прямым углом к оси Земли.
Наклонными– под любым другим (непрямым) углом к оси Земли.

Нормальная, поперечная и косая ориентации площади проекции. Автор: Rylem

Поверхности, которые могут быть развёрнуты на плоскость или лист без растяжений, разрыва или усадки, называются разрабатываемыми поверхностями. Ими являются цилиндр, конус и плоскость. Поэтому по вспомогательной поверхности проекции делятся на:

цилиндрические – вспомогательная поверхность – боковая цилиндра, касательная к эллипсоиду или секущая эллипсоида. Меридианы изображаются равностоящими параллельными прямыми, а параллели – прямыми, перпендикулярными меридианам. Пример – нормальная равноугольная цилиндрическая проекция Меркатора.

Цилиндрическая, коническая, азимутальная типы проекций.
Автор: Rylem — собственная работа, CC BY-SA 4.0

псевдоцилиндрические – центральный меридиан на них представлен в виде отрезка прямой, другие меридианы длиннее центрального и изогнуты наружу. Параллели псевдоцилиндрических проекций – прямые линии.

Псевдоцилиндрическая проекция

конические – боковая поверхность секущей или касательной конуса. Конической называется любая проекция, в которой меридианы представлены прямыми линиями, выходящими из одного центра и равноудаляющимися к периферии, а параллели – дуги, центрированные на вершине. При построении картографы чаще выбирают 2 основные параллели, которые могут быть секущими или касательными. Искажения масштаба и формы на них низкие. К северу и югу от стандартных параллелей расстояния растягиваются, а между стандартными параллелями расстояния сжимаются. Может использоваться и одна стандартная параллель, тогда с удалением от неё расстояния растягиваются. Применяется для территорий, вытянутых вдоль параллелей, например, все карты России построены в конических проекциях.
псевдоконические – проекции, где центральный меридиан – прямая, остальные меридианы кривые линии, а параллели – прямые, промежутки между которыми уменьшаются к полюсам.
азимутальные – вспомогательной поверхностью служит секущая или касательная плоскость. Параллели на них – полные окружности. Меридианы – их радиусы. По меридианам такая проекция является равнопромежуточной и сохраняет вдоль них главный масштаб. Именно разновидностью азимутальной проекции является первая известная на Земле гномическая проекция.

Типы азимутальных проекций

поликонические – боковые вспомогательные поверхности нескольких касательных конусов, каждая из которых затем разворачивается на плоскость. Экватор и средний меридиан – перпендикулярные прямые, параллели – дуги, выпуклостью направленные к экватору, меридианы – кривые малой кривизны, направленные выпуклой стороной от центрального меридиана.
условные – те, что ни входят ни в один из выше перечисленных классов. Параллели и меридианы на них являются кривыми очень разного вида.

Полное название проекций может быть следующим: косая азимутальная равновеликая, нормальная равноугольная цилиндрическая, произвольная поликоническая и т.д.

Источник