Способ проектного полигона геодезия

Способы разбивочных работ

Способ прямой и обратной угловых засечек. Чаще всего эти способы применяют для выноса недоступных точек, а также точек, находящихся на значительных расстояниях от геодезической основы.

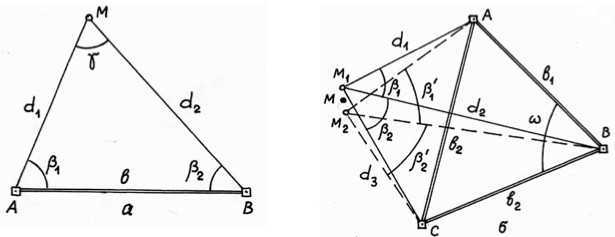
В способе прямой угловой засечки (см. рис. а) положение точки М определяют с исходных пунктов А и В геодезической основы построением в каждой из них горизонтальных углов β1 и β2, которые являются разбивочными элементами. Указанные углы строят на местности по правилам, изложенным в § 88. В данной схеме целесообразно использовать одновременно два теодолита. При этом положение проектной точки фиксируют по команде двух наблюдателей при положениях КЛ, а затем – при положениях КП. После фиксирования среднего положения точки М выполняют контрольное измерений углов β1 и β2.

Необходимо иметь в виду, что величина угла γ при точке М не должна быть малой и слишком большой. Оптимальным углом, при котором вынос точки может быть выполнен с меньшей погрешностью, является γ ≈109 0 − 110 0 при примерно равных расстояниях от исходных точек до точки М. То есть следует стремиться обеспечить симметричную схему построения точки М. Кроме того, для повышения точности построения проектной точки, а также для контроля её построения, вынос проектной точки на местность выполняют часто с двух базисов геодезической разбивочной основы.

Во многих случаях бывает сложно из одного приема вынести точку М с заданной точностью в её проектное положение. В таких случаях используют способ замкнутого треугольника. Вынос точки осуществляют последовательными приближениями. Для этого с максимально возможной точностью выполняют построение точки М, затем несколькими приёмами измеряют все углы треугольника, уравнивают углы и вычисляют координаты точки М из решения по формулам прямой угловой засечки. Полученные координаты сравнивают с проектными и при недопустимых отклонениях в их значениях определяют поправки (редукции) в положение точки М и смещают последнюю в проектное положение. Для контроля снова измеряют углы и выполняют аналогичные вычисления.

Вынос проектной точки способами прямой и обратной угловых засечек: а) способ прямой угловой засечки; б) способ обратной угловой засечки

Вынос на местность проектной точки способом полярных координат

Вынос на местность проектной точки способом проектного полигона

Метод последовательных приближений используют и в способе обратной угловой засечки (см. рис. б). Предварительно точку М выносят на местность и измеряют при ней углы β1 и β2. По формулам обратной угловой засечки определяют координаты точки М и сравнивают их с проектными. При необходимости положение точки М редуцируют на величины отклонений по координатам Х и Y, точку М фиксируют в положении М₂ и снова уже в новой точке измеряют горизонтальные углы β а затем вычисляют координаты новой точки М. Все указанные действия выполняют до тех пор, пока задача качественного построения проектной точки не будет решена.

Способ полярных координат используют в тех случаях, когда проектные точки находятся сравнительно недалеко от точек геодезической основы. При этом предпочтительно, чтобы расстояния до них не превышали длины мерного прибора (ленты или рулетки).

На местности от исходного направления АВ (см. рис.) строят проектный угол β и проектное расстояние d, которые в данном способе являются разбивочными элементами.

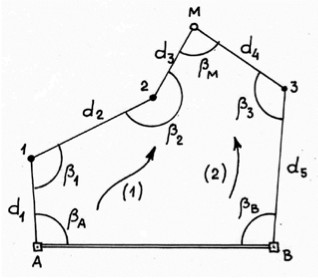
Проектная точка может находиться далеко от точек геодезической основы или не может быть вынесена по техническим условиям способами угловой засечки. В таких случаях к точке прокладывают полигонометрический ход (см. рис.), используя для этого последовательно расчётные проектные углы и проектные расстояния. Данный способ называют способом проектного полигона.

По двум ходам от базисной линии АВ геодезической основы получают два положения точки М из решения ходов (1) и (2). В качестве первого приближения вычисляют средние значения координат проектной точки. Затем в полученной точке М измеряют угол β_М и линии d₃ и d₄ и вычисляют координаты точки М в общей схеме замкнутого полигона. Если координаты точки М будут значительно отличаться от проектных, то определяют поправки (редукции) в положение точки М, точку смещают и снова измеряют угол β_М и линии d₃ и d₄. Из решения хода находят координаты точки М и сравнивают их с проектными. Такие действия выполняют до достижения необходимой точности построения проектной точки.

Вынос на местность проектной точки способом линейной засечки

Способы створных засечек: а) способ створно-линейной засечки; б) способ створной засечки

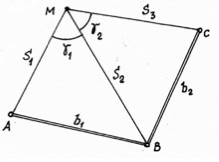
При небольших расстояниях от проектной точки до точек геодезической основы удобно использовать способ линейной засечки, реализуемый с помощью двух или трёх рулеток (см. рис.). Разбивочными элементами в этом способе являются только расстояния S или горизонтальные проложения.

Для выноса осей сооружений удобно использовать способы створных засечек (см. рис.).

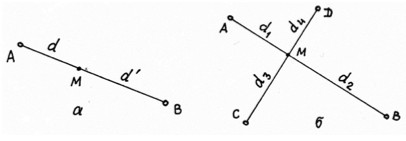
В схеме створно-линейной засечки (см. рис. а) положение точки М определяют на линии створа, образованного пунктами А и В геодезической основы. По линии створа проектным расстоянием d задают положение искомой точки М. При необходимости положение точки М может быть проконтролировано с другой точки створа. В точке А створа устанавливают теодолит, а в точке В – визирную цель (на штативе, с возможностью центрирования и горизонтирования).

В схеме створной засечки (см. рис. б) точку М задают на линии пересечения створов АВ и СD. Для повышения точности работу целесообразно выполнять одновременно двумя теодолитами и двумя визирными целями несколькими приёмами с перестановкой теодолитов и визирных целей. Для контроля измеряют расстояния от построенной точки до исходных пунктов геодезической основы.

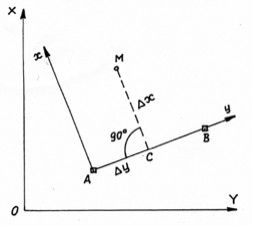
Обычно на строительной площадке имеется т.н. строительная сетка. В её системе координат задано положение всех осей (главных, основных и т.д.), а также всех главных (узловых) точек. В этом случае вынос проектных точек осуществляется в системе координат строительной сетки по приращениям координат Δx и Δy (см. рис.). В общегосударственной или местной системах координат ХОY используется система координат хАy строительной сетки c началом координат в точке А. Ось Аy задается исходным направлением на другую исходную точку (В) геодезической основы. Положение точки М определяется расстояниями Δx и Δy, т.е. приращениями координат в системе координат строительной сетки.

Разбивка точек сооружения от строительной сетки

Способ бокового нивелирования

Предварительно строят проектное расстояние Δy, устанавливают в полученной точке С теодолит, строят проектный угол β, равный 90 0 на точку М и в полученном направлении откладывают отрезок Δx. Для обеспечения более высокой точности построения точки меньшее из Δx и Δy следует строить в виде перпендикуляра, а большее – по створу исходной линии.

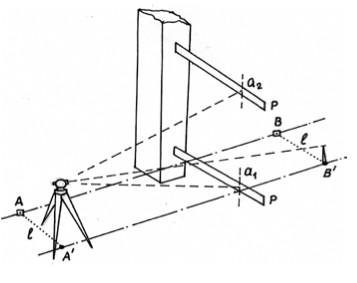
Вынос вертикальных осей конструкций выполняют способом бокового нивелирования (см. рис.). От оси АВ, на которой находится строительная конструкция, например, колонна, а небольшом расстоянии l строят линию А’В’, параллельную исходной линии АВ. В точке А’ устанавливают теодолит, который визируют на марку, находящуюся в точке В’. Перпендикулярно к оси колоны последовательно на её основание и верх устанавливают рейку Р (с уровнем, ориентированным осью по продольной оси рейки) и берут отсчёты а₁ и а₂ по вертикальной нити сетки зрительной трубы. Равенство указанных отсчётов определяет вертикальность оси колонны. Если расхождение между отсчётами недопустимо, то положение вертикальной оси колонны выправляют.

Оставьте свой отзыв, комментарий или задайте вопрос

Источник

Способ проектного полигона

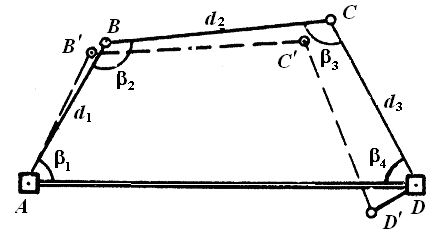
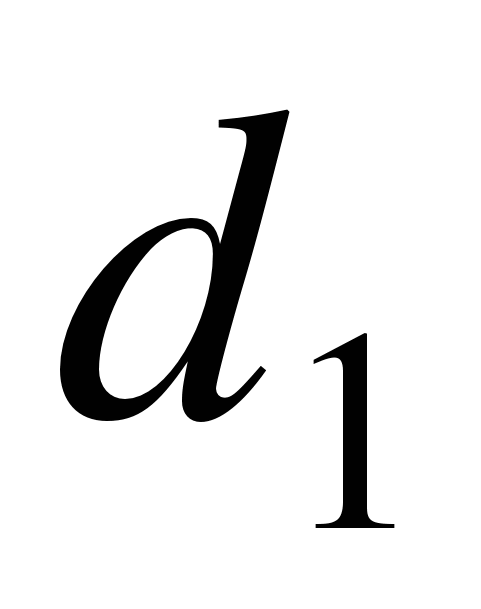
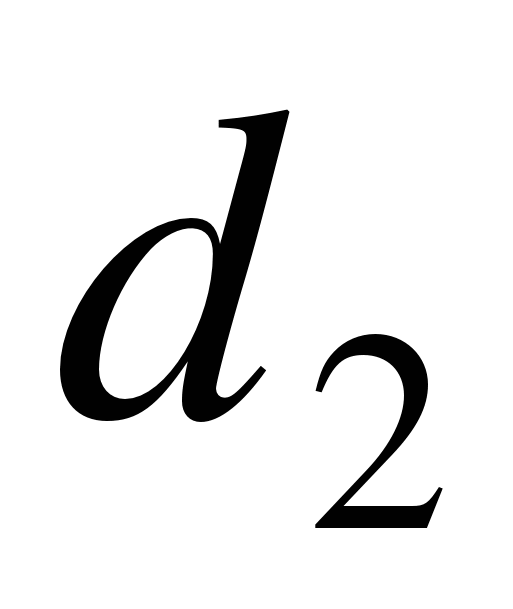
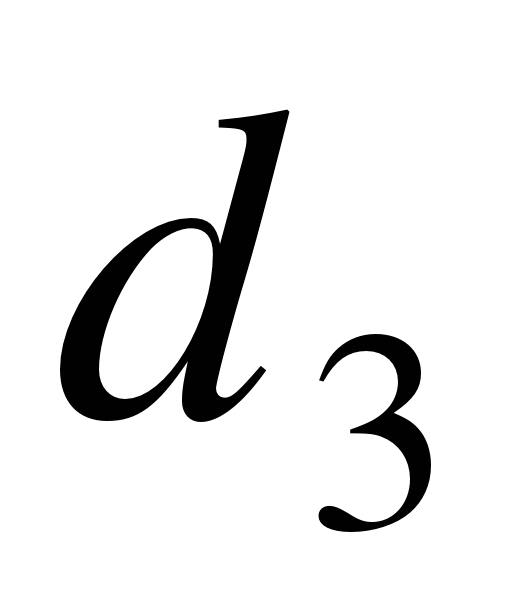
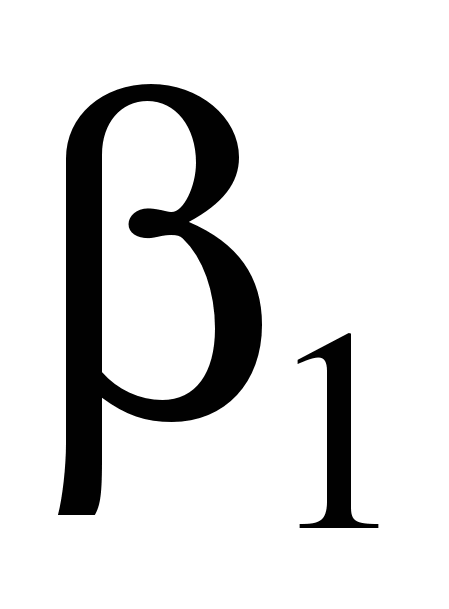
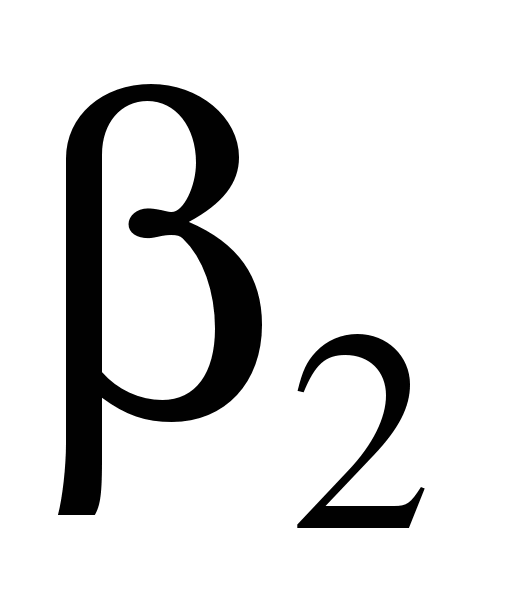
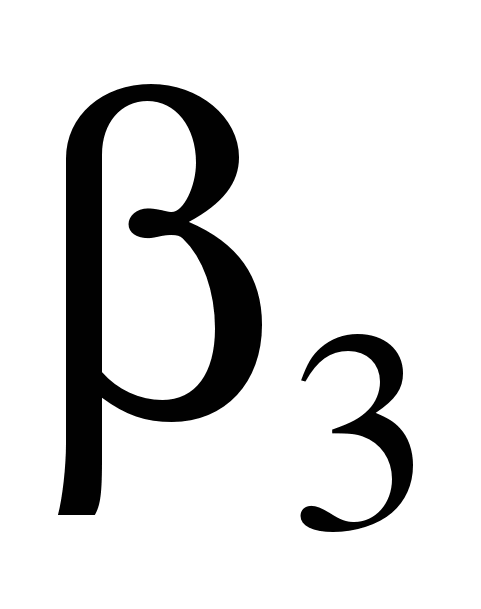
Способ проектного полигона применяют для выноса в натуру нескольких точек, если расстояния между ними не слишком велики. Из решения обратной геодезической задачи находят длины сторон , и и внутренние углы проектного полигона , , и (рис. 1.24). Затем, откладывая углы и расстояния, последовательно находят положения точек В¢, C¢и D¢, которые вследствие погрешностей построения углов и расстояний не совпадут с проектными точками.

Рис. 1.24. Построение точек способом проектного полигона

В конечной точке D¢измеряют величину и магнитный азимут направления линейной невязки DD¢. Если невязка не превышает допустимого значения, то точки В¢, С¢и D¢спомощью линейки перемещают в проектное положение по направлению магнитного азимута DD¢ на расстояния, пропорциональные их удалению от начала хода:

, .

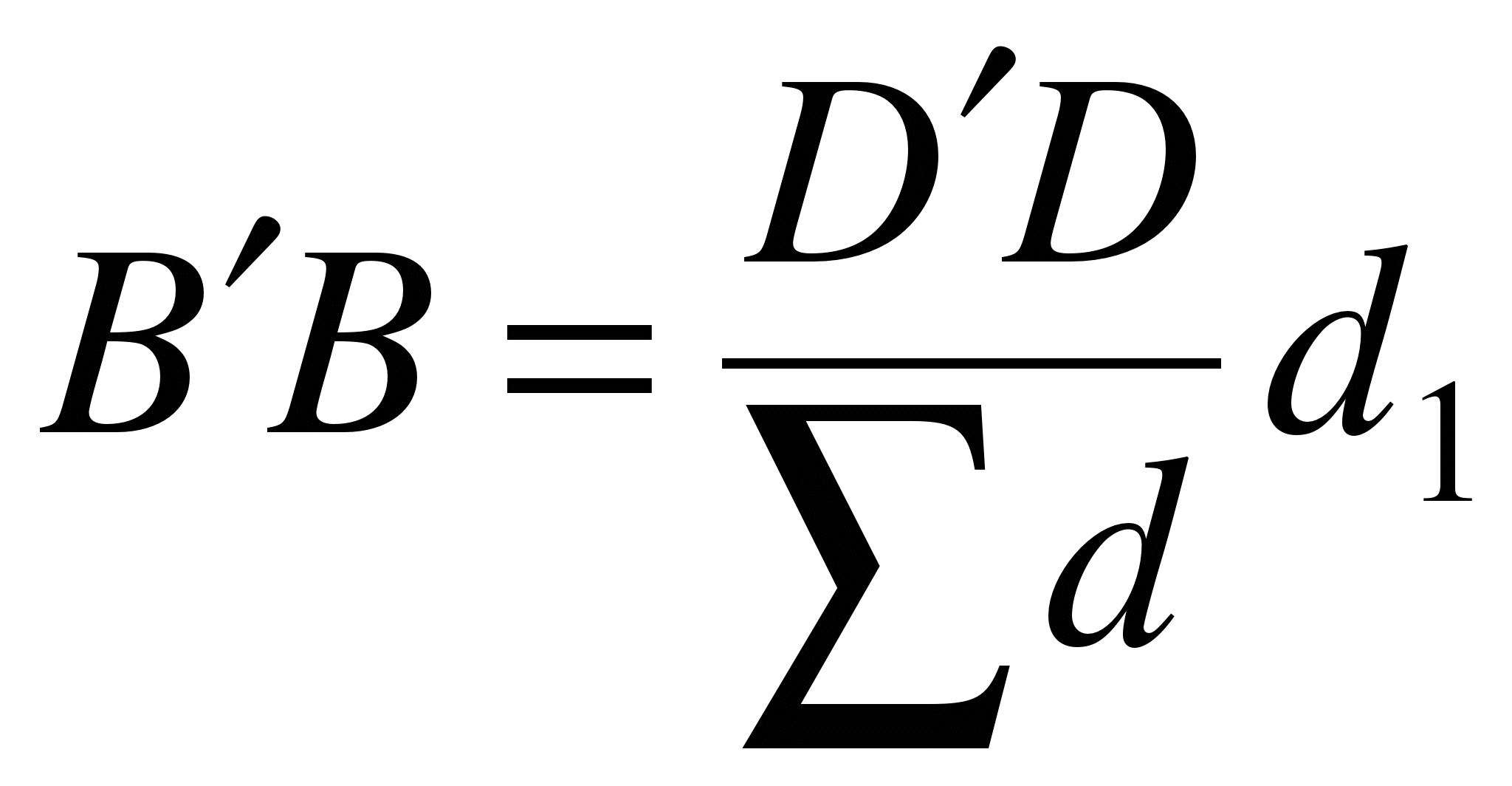
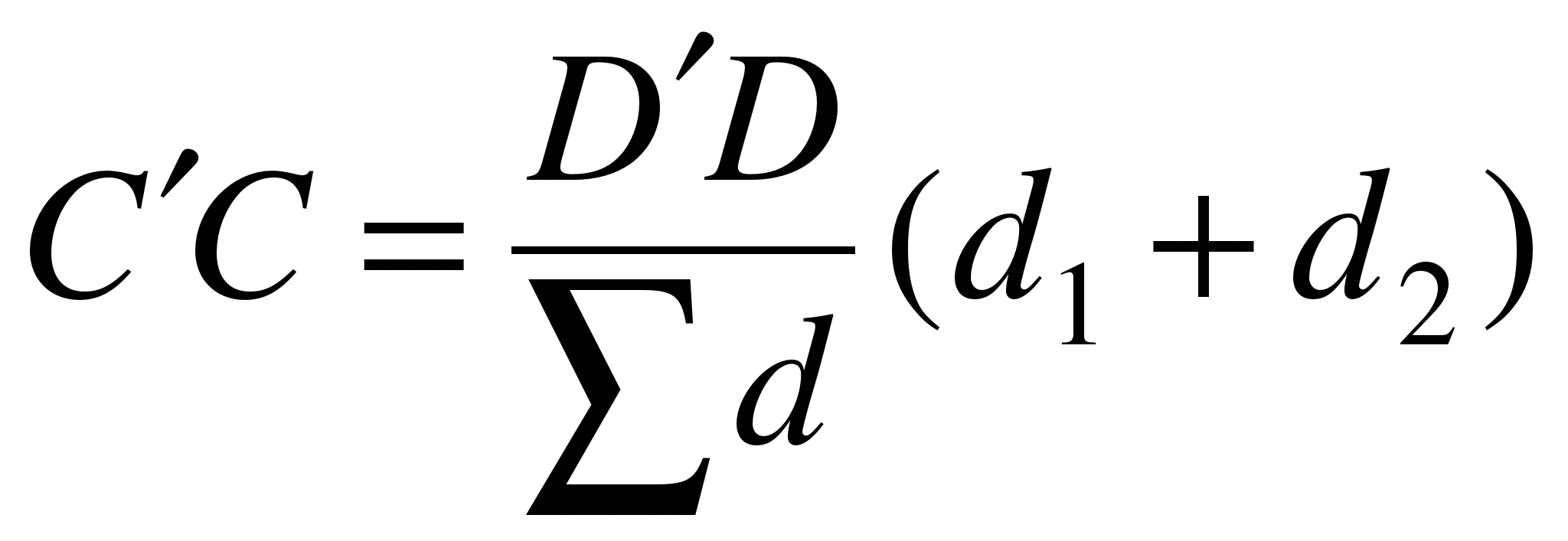
Полученные точки закрепляют.

33Альманах (спутн. навигац.) – набор данных об орбите, траектории и ходе часов навигационного спутника (системы NAVSTAR/GPS, ГЛОНАСС и др.). Альманах включается в сообщение, которое спутник передает на наземные станции, и отсылается на Землю еженедельно.

Альманах используется при спутниковых геодезических измерениях и в навигации для того, чтобы дать информацию о том, в какой части сферы можно ожидать спутник и в какое время. Таким образом, для GPS/ГЛОНАСС-приемника облегчается задача поиска супутника.

Сообщение альманаха включает такие сведения данные:

— «грубые», по сравнению с эфемеридами, данные об орбите

— данные о ходе часов спутника – поправка часов в эпоху и дрейф часов.

Источник

5 Основные методы и способы разбивочных работ

Основные методы и способы разбивочных работ

Разбивка отдельных элементов сооружения ведется с хорошо закрепленных на местности точек и линий опорной сети или с то­чек главных разбивочных осей сооружения.

В разбивке могут быть использованы способы прямоугольных координат (перпендикуляров), полярных координат, биполярных координат (угловых, линейных, комбинированных и створных засечек), створов и промеров.

Разбивка и перенесение проектов сооружений в натуру по своим действиям обратным геодезическим съемочным работам.

Способ угловой засечки применяют для разбивки недоступных точек, находящихся на значительном расстоянии от исходных пу­нктов.

Различают прямую и обратную угловые засечки.

В способе прямой угловой засечки положение на местности про­ектной точки С (рисунок 6) находят отложением на исходных пунктах А и В проектных углов β₁ и β₂. Базисом засечки служит или специально измеренная сторона, или сторона разбивочной сети. Проектные углы β₁ и β₂ вычисляют как разность дирекционных углов сторон. Дирекционные углы находят из решения обратной геодезической задачи по проектным координатам определяемой точки и известным координатам исходных пунктов.

Рекомендуемые файлы

Рисунок 6 — Схема разбивки способами прямой угловой и линейной засечек

На точность разбивки способом прямой угловой засечки оказы­вают влияние ошибки собственно прямой засечки, исходных дан­ных, центрирования теодолита и визирных целей, фиксации раз­бивочной точки, т.е.

. (14)

Средняя квадратическая ошибка собственно засечки равна

(15)

, (16)

где m_β — средняя квадратическая ошибка отложения углов β₁ и β₂.

Для приближенных расчетов принимают S₁ = S₂ = S. Тогда формула (16) будет иметь вид:

. (17)

При разбивочных работах центрирование теодолита и визирных целей с помощью оптических отвесов, фиксация выносимой точки могут быть выполнены сравнительно точно. Поэтому основными ошибками, определяющими точность способа прямой угловой за­сечки, являются ошибки собственно засечки и исходных данных. Суммарная величина этих ошибок составит:

. (18)

На принципе редуцирования основано и применение для разбив­ки способа обратной угловой засечки. На местности находят прибли­женно положение О’ разбиваемой проектной точки О (рисунок 7). В этой точке устанавливают теодолит и с требуемой точностью измеряют углы не менее чем на три исходных пункта с известными координатами. По формулам обратной засечки вычисляют коор­динаты приближенно определенной точки и сравнивают их с про­ектными значениями. По разности координат вычисляют величины редукции (угловой и линейный элементы) и смещают точку в проектное положение. Для контроля на этой точке измеряют углы, вновь вычисляют ее координаты и сравнивают их с проектным. В случае недопустимых расхождений все действия повторяют.

Для вычисления координат точки О’ можно использовать формулы Деламбера и Гаусса. Применительно к (рисунок 7), они будут иметь вид:

(19)

(20)

На точность разбивки способом обратной угловой засечки ока­зывают влияние ошибки собственно засечки, исходных данных, центрирования теодолита и визирных целей, фиксации разбивочной точки и редуцирования. Очевидно, что при сравнительно больших расстояниях от определяемого до опорных пунктов влияние первых двух источников будет наиболее существенным; остальными ошиб­ками можно пренебречь.

Рисунок 7 — Схема способа обратной угловой засечки

Ошибка собственно обратной засечки может быть подсчитана по приближенной формуле:

(21)

где S — расстояние от определяемо­го до соответствующих опорных пунктов;

b — расстояние между соответ­ствующими опорными пунктами;

ω_bac — угол между исходными сто­ронами.

Ошибки исходных данных учиты­вают по формуле:

(22)

В способе линейной засечки положение выносимой в натуру точки С (рисунок 6) определяют в пересечении проектных рассто­яний S₁ и S₂, отложенных от исходных точек А и В. Этот способ обычно применяют для разбивки осей строительных конструкций в случае, когда проектные расстояния не превышают длины мер­ного прибора.

Наиболее удобно разбивку производить при помощи двух руле­ток. От точки А по рулетке откладывают расстояние S₁, а от точки В по второй рулетке – S₂. Перемещая обе рулетки при совмещен­ных нулях с центрами пунктов А и В, на пересечении концов отрезков S₁ и S₂ находят положение определяемой точки С.

Ошибка собственно линейной засечки при одинаковой точности m_s отложения расстояний S₁ и S₂ может быть подсчитана по формуле:

. (23)

Минимальной ошибка собственно линейной засечки будет при угле γ = 90°. В этом случае

. (24)

Влияние ошибок исходных данных в линейной засечке выражается формулой:

. (25)

. (26)

В случае применения мерных приборов ошибки центрирования отсутствуют. Тогда общая ошибка в определении положения раз­биваемой точки С будет в основном зависеть от суммарной ошибки собственно засечки и исходных данных и выражаться формулой:

. (27)

Для приближенных расчетов, приняв γ = 90°, будем иметь

. (28)

В случае, если для линейной засечки применяются дальномерные комплекты, которые центрируются при помощи штативов, то влия­ние ошибок центрирования можно определить по формуле:

. (29)

Способ полярных координат широко применяют при разбивке осей зданий, сооружений и конструкций с пунктов теодолитных или полигонометрических ходов, когда эти пункты расположены срав­нительно недалеко от выносимых в натуру точек.

В этом способе положение определяемой точки С (рисунок 8) находят на местности путем отложения от направления АВ проектного угла β и расстояния S. Проектный угол β находится как разность дирекционных углов α_АВ и α_АС, вычисленных как и расстояние S из решения обратных задач по координатам точек А, В и С. Для контроля поло­жение зафиксированной точки С можно проверить, измерив на пункте В угол β’ и сравнив его со значением, полученным как разность дирекционных углов α_ВА и α_вс.

Средняя квадратическая ошибка выноса в натуру точки С определяется формулой

. (30)

Рисунок 8 — Схема разбивки способом полярных координат

Ошибка собственно разбивки полярным способом зависит от ошибки т_β построения угла β и ошибки m_s отложения проектного расстояния S

. (31)

Влияние ошибок исходных данных при т_А = т_в = т_АВ выражается формулой:

, (32)

а ошибок центрирования

. (33)

Формулы (32) и (33) аналогичны. Из них следует, что для уменьшения влияния ошибок исходных данных и центрирования необходимо, чтобы угол β и отношение S/b были минимальны, полярный угол был бы меньше прямого, а проектное расстоя­ние – меньше базиса разбивки, т. е. β 90°, S b.

Для приближенных расчетов, приняв β = 90° и S = b, получим

(34)

а для суммарной ошибки в положении точки, разбиваемой способом полярных координат,

(35)

Если разбиваемая точка находится на значительном расстоянии от исходного пункта, то приходится несколько раз откладывать полярным способом проектные углы и расстояния, прокладывая проект­ный ход (рисунок 9). При наличии пря­мой видимости с точки С на точку В для контроля измеряют примычные углы γ₁ и γ₂, образуя замкнутый уг­ловой полигон. Поэтому такой способ называют способом проектного поли­гона. При точных разбивочных рабо­тах углы полигона уравнивают, вычи­сляют по ним и проектным расстоя­ниям координаты точки С, сравнива­ют их с проектными и при необходи­мости редуцируют в проектное положение.

Рисунок 9 — Схема разбивки способом проектного полигона

При редкой разбивочной основе способ проектного полигона может быть использован для разбивки всех точек пересечения ос­новных осей сооружения от одного исходного пункта. В этом случае проектный ход с проектными углами и расстояниями прокладыва­ют полностью.

Способы створной и створно-линейной засечек широко применя­ют для выноса в натуру разбивочных осей зданий и сооружений, а также монтажных осей конструкций и технологического оборудо­вания.

Положение проектной точки С в способе створной засечки определяют на пересечении двух створов, задаваемых между исходными точками 1-1′ и 2-2′ (рисунок 10). Створ задают обычно теодоли­том, который центрируют над исходным пунктом (например, 1), а зрительную трубу ориентируют по визирной цели, отцентриро­ванной на другом исходном пункте (в данном случае — 1′). Положе­ние точки С фиксируют в заданном створе.

Средняя квадратическая ошибка створной засечки зависит от ошибок построения первого m_с1, и второго m_c2 створов, а также ошибки фиксации

. (36)

Рисунок 10 — Схемы разбивки способами створной (а) и

створно-линейной (б) засечек

Основными ошибками при построении каждого из створов явля­ются ошибки положения исходных точек, ошибки центрирования теодолита и визирных целей, ошибка визирования и перемены фокусировки зрительной трубы при наведении на визирную цель и на определяемую точку, т.е.

. (37)

Ошибки положения исходных точек для задания створа имеют значения только в направлении, перпендикулярном створу, т. е. для каждого створа по одной из координат х или у. Их влияние определяется формулой:

, (38)

где d — расстояние от точки установки теодолита до определяемой точки;

S — расстояние между исходными точками (длина створа).

Совместное влияние ошибок центрирования теодолита и визир­ной цели выражается формулой:

. (39)

Анализируя формулы (38) и (39), можно сделать вывод, что наименьшее влияние ошибки исходных данных и центрирования оказывают на положение определяемой точки в середине створа. По мере приближения ее к исходным пунктам эти ошибки возрастают.

При построении створа приходится визировать дважды: вначале на визирную цель, установленную на исходной точке, затем на цель, фиксирующую положение разбиваемой точки в створе. В обоих случаях линейная величина ошибки визирования для определяемой точки будет пропорциональна расстоянию d от теодолита до этой точки. Следовательно, для створных построений ошибка визирова­ния (в мм) будет равна

. (40)

При построении створа приходится визировать на точки, расположенные от теодолита на разных расстояниях, что приводит к необходимости менять фокусировку трубы. Изменение хода фоку­сирующей линзы вызывает смещение визирной оси трубы и приво­дит к ошибке, которую необходимо учитывать при точных работах.

В современных высокоточных теодолитах ошибка из-за перефокусировки трубы примерно равна ошибке визирования. Поэтому для приближенных расчетов можно принять т_фок = т_виз. С учетом этого совместное влияние ошибок визирования и фокусирования при створных построениях может быть выражено формулой:

. (41)

Створно-линейный способ позволяет определить проектное положение выносимой в натуру точки С (рисунок 10) путем отложения проектного расстояния d по створу АВ.

Способ прямоугольных координат применяют в основном при наличии на площадке или в цехе промышленного предприятия строительной сетки, в системе координат которой задано положе­ние всех главных точек и осей проекта.

Разбивку проектной точки С (рисунок 11) производят по вычислен­ным значениям приращений ее координат ∆х и ∆у от ближайшего пункта сетки. Большее приращение (на рисунке – ∆у) откладывают по створу пунктов сетки АВ. В полученной точке D устанавливают теодолит и строят от стороны сетки прямой угол. По перпен­дикуляру откладывают меньшее приращение и закрепляют полу­ченную точку С. Для контроля положение точки С можно опреде­лить от другого пункта строительной сетки.

Схема способа прямоугольных координат по существу сочетает в себе схему створно-линейного и полярного способов.

Рисунок 11 — Схема разбивки способом прямоугольных координат

Средняя квадратическая ошибка в положении точки С, определенной способом прямоугольных координат, может быть выражена формулой:

, (42)

где m_∆x, и т_∆у — ошибки отложения приращения координат.

Если по перпендикуляру откладывается ордината, то в формуле (42) величина ∆х заменяется на ∆у.

Влияние ошибок в положении исходных пунктов при условии т_A = т_B = m_AB выражается формулой:

, (43)

а ошибок центрирования

, (44)

где b — длина стороны строитель­ной сетки.

Источник